-
With the development of infrared detectors and radiometry technology, IR radiometric systems have gradually become active[1]. Infrared radiometry based on image grayscale is an indirect method[2]. For a target with a certain distance in space, the transmitted infrared radiation of the target is attenuated, due to the absorption and scattering of water vapor, carbon dioxide, aerosol and other components in the atmosphere[3]. The atmospheric transmittance is brought forward to describe this process. The radiation emitted by various components of the atmosphere is superimposed on the target radiation and transfer into the measurement system, and this process can be described as the atmospheric path radiation as well[4]. For high-precision radiometry, these two factors mentioned above should be considered as important influences affecting the measurement accuracy. Existing measurement methods of the atmospheric transmittance include software calculation, theoretical numerical calculation and standard reference source measurement, etc. The software calculation is a widely used approach by inputting relevant atmospheric environmental parameters. The atmospheric transmittance is simply and expediently obtained from the atmospheric radiation transfer software. It is the most direct way but the real-time measurement error is relatively mediocre even more than 20% sometimes. With known parameters, such as atmospheric component content and spectral line intensity, numerical calculation with use of radiation transfer model is the most accurate method, such as line-by-line integration method[5]. However, the large amount of calculation and time-consuming are not suitable for practical application. Near-range standard reference source measurement (NRsrM) is the calculation of atmospheric transmittance using a standard reference target known for temperature or infrared radiance with a measurement precision of 5%[6]. However, the measurement range of this method is extremely limited so that it is only suitable for close range measurement, and the reference source cannot be placed near the target in practical application.
The real-time measurement method based on NRsrM is relatively simple, and meets the accuracy requirements in practical application. The transmittance and path radiation obtained from the atmospheric radiation transfer software according to historical data are also well-founded. Therefore, a nonlinear atmospheric correction (NLAC) method based on NRsrM and software calculation is proposed to achieve measuring the atmospheric transmittance and path radiation simultaneously in this paper. The main advantage of this method is that it can realize infrared radiation measurement of long distance targets using the nonlinear fitting technology of neural network. Long-range atmospheric transmittance and path radiation are corrected by near-range measurement, thus it can improve the accuracy of target radiation measurement compared to the result obtained from the software. Linear atmospheric correction (LAC) method and linear enhancement atmospheric correction (LEAC) are compared with the method presented as well in this paper, the accuracy of infrared radiation measurement is improved obviously based on the analysis of the experimental data.
-
The target infrared radiation process is shown in Fig. 1. The sources of radiation energy received by infrared system include target radiation attenuated through atmosphere, target reflection radiation to surrounding environment attenuated through atmosphere, also called equivalent background radiation, and atmospheric self-radiation between optical system and target[7- 8]. For an opaque target, the infrared radiance entering infrared system can be described as following formula:
$${L_{t,\rm{atm}}} = {\tau _{\rm{atm}}} \cdot \varepsilon \cdot L({T_t}) + {\tau _{\rm{atm}}} \cdot (1 - \varepsilon ) \cdot L({T_e}) + {L_{\rm{path}}}$$ (1) where
${\tau _{\rm{atm}}}$ is the atmospheric transmission,$\varepsilon $ is the measured target emissivity,${L_{t,\rm{atm}}}$ is the infrared radiance entering infrared system,$L({T_t})$ stands for the radiative contribution from the target,$L({T_e})$ stands for the radiative contribution from the surrounding environment, and${L_{\rm{path}}}$ stands for the atmospheric self-radiation between the infrared system and the target.The radiation flux received by a detector element through the optical system is
$${\varPhi _{t,i,j}} = \frac{{\text{π} \cdot {\tau _{\rm{opt}}}}}{4} \cdot {\left( {\frac{D}{f}} \right)^2} \cdot {A_{\rm{d}}} \cdot {L_{t,\rm{atm}}} = {k_t} \cdot {L_{t,\rm{atm}}}$$ (2) where
${\tau _{\rm{opt}}}$ is the transmittance of the optical system,$D$ is the diameter of the optical system,$f$ is the focal length,${A_{\rm{d}}}$ is sensitive area of a detector element, hence${k_t} = (\text{π} \cdot {\tau _{\rm{opt}}}/4){(D/f)^2} \cdot {A_{\rm d}}$ is constant for a given infrared system.When the infrared radiation measurement system imagines a target at a certain distance, the gray image can be obtained from the electrical signal converted from the infrared radiation. Infrared systems, in many applications, are operated in a range of radiance within which detectors exhibit linear input–output characteristics. The output gray value [digital number (DN)] at a preselected integration time is given by the approximate linear relation:
$${G_{i,j}} = {k_{i,j}} \cdot {\varPhi _{t,i,j}} + {B_{i,j}} = {K_{i,j}} \cdot {L_{t,{\rm{atm}}}} + {B_{i,j}}$$ (3) where
${G_{i,j}}$ is the gray value of the$(i,j)$ th detector in the array,${K_{i,j}} = {k_{i,j}} \cdot {k_t}$ is the incident radiance response of infrared measurement system,${B_{i,j}}$ is the offset, originating from the stray radiation that strike the detector element, and internal factors of the detector, such as dark current. The following formula can be written according to Eq. (1) and (3):$${G_{i,j}} = {K_{i,j}} \cdot \left[ {{\tau _{{\rm{{\rm{atm}}}}}} \cdot \varepsilon \cdot L({T_t}) + {\tau _{{\rm{atm}}}} \cdot (1 - \varepsilon ) \cdot L({T_e}) + {L_{{\rm{path}}}}} \right] + {B_{i,j}}$$ (4) The inverted radiance of the target obtained from Eq. (4) can be described as follows:
$$L({T_t}) = \frac{{{G_{i,j}} - {B_{i,j}} - {K_{i,j}} \cdot {L_{{\rm{path}}}} - {K_{i,j}} \cdot {\tau _{{\rm{atm}}}} \cdot (1 - \varepsilon ) \cdot L({T_e})}}{{{K_{i,j}} \cdot {\tau _{{\rm{atm}}}} \cdot \varepsilon }}$$ (5) where
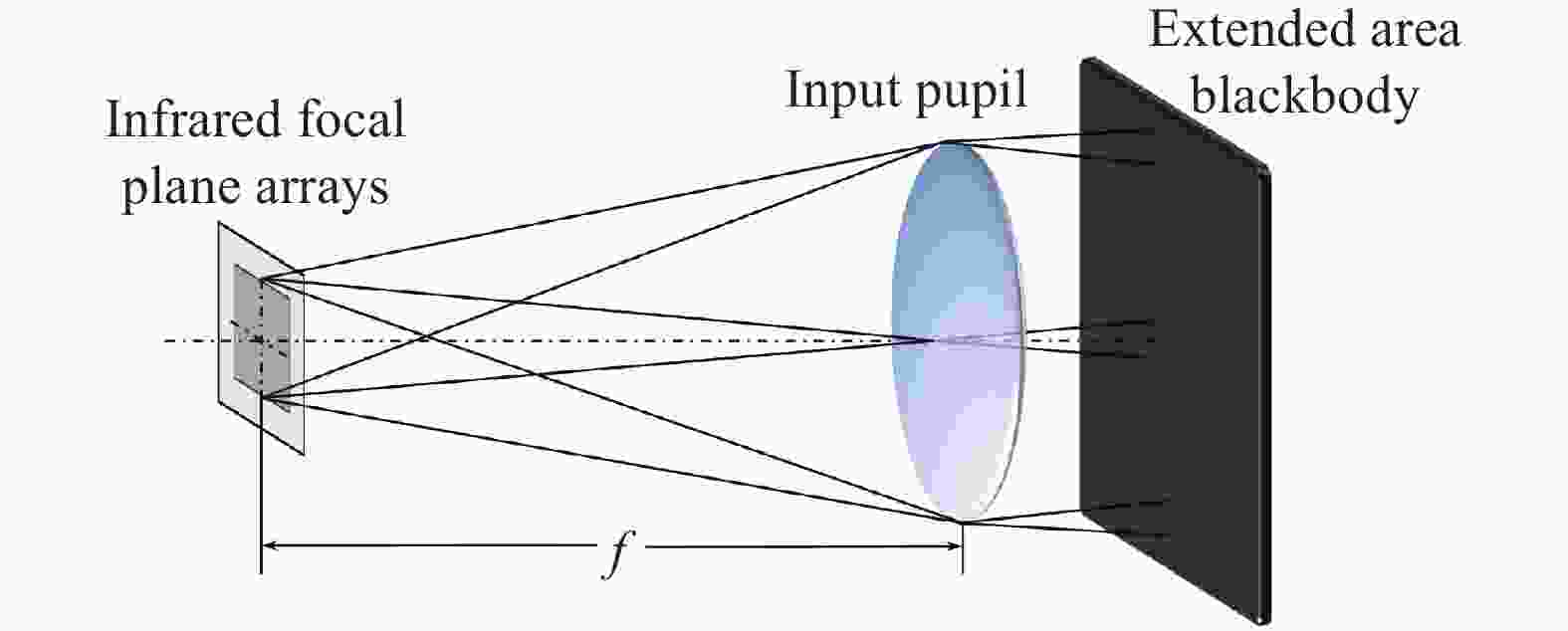
${{\rm{K}}_{i,j}}$ and${B_{i,j}}$ can be accurately measured by the near-extend-source method for calibration at a preselected integration time[9- 10]. The geometric model of calibration is illustrated in Fig. 2. If the measured target emissivity$\varepsilon $ is known in advance, and the equivalent background radiation$L({T_e})$ can be measured as well, the target radiation can be calculated from Eq. (5) by collecting the target image${G_{i,j}}$ and measuring the atmospheric transmission${\tau _{{\rm{atm}}}}$ and path radiation${L_{{\rm{path}}}}$ . -
It is known from the measurement principle that the accuracy of the atmospheric transmittance and path radiation play an extremely crucial role in infrared radiometry compared to other parameters, such as the response and offset, which are determined by a given infrared measurement system. In the conventional radiometric method, the atmospheric transmittance and path radiation are calculated by atmospheric radiation transfer software. However, the error of this method is not able to meet the application requirements. Atmospheric correction method for the atmospheric transmittance and path radiation is desirable to improve the infrared radiometric accuracy.
-
Figure 3 shows the schematic of an experimental setup for NRsrM. An ideal blackbody whose emissivity is close to 1 as a standard reference source is placed at a distance of
${l_0}$ from the infrared imaging system. Infrared images of the ideal blackbody can be captured at temperatures of${T_l}$ and${T_h}$ , respectively. Ignoring the index of the detector element above, the gray value of the ideal blackbody can be described as follows simplified from Eq. (4).$${G_l} = K \cdot \left[ {{\tau _{{\rm{atm}},{l_0}}} \cdot L({T_l}) + {L_{{\rm{path}},{l_0}}}} \right] + B$$ (6) $${G_h} = K \cdot \left[ {{\tau _{{\rm{atm}},{l_0}}} \cdot L({T_h}) + {L_{{\rm{path}},{l_0}}}} \right] + B$$ (7) where
${G_l}$ and${G_h}$ are the gray value of the ideal blackbody at temperatures of${T_l}$ and${T_h}$ , respectively,$K$ and$B$ are the response and offset of infrared measurement system,${\tau _{{\rm{atm}},{l_0}}}$ and${L_{{\rm{path}},{l_0}}}$ denote the atmospheric transmittance and path radiation between the measured blackbody and the infrared system, respectively,$L({T_l})$ and$L({T_h})$ denote the in-band radiance of the ideal blackbody at the same absolute temperature${T_l}$ and${T_h}$ , respectively, which can be calculated by Planck’s formula integral. The actual atmospheric transmittance and path radiation can be calculated at the distance${l_0}$ from Eq. (6) and Eq. (7).$${\tau _{{\rm{atm}},{l_0}}} = \frac{{{G_h} - {G_l}}}{{K \cdot \left[ {L({T_h}) - L({T_l})} \right]}}$$ (8) $${L_{{\rm{path}},{l_0}}} = \frac{{L({T_h}) \cdot ({G_l} - B) - L({T_l}) \cdot ({G_h} - B)}}{{K \cdot \left[ {L({T_h}) - L({T_l})} \right]}}$$ (9) -
MODTRAN (moderate resolution atmospheric transmission) is a commercial atmospheric radiative transfer model developed by the U.S. Air Force[11]. The theoretical atmospheric transmittance and path radiation at the distance
${l_0}$ calculated by MODTRAN4.0 are$\tau _{{\rm{atm}},{l_0}}'$ and$L_{{\rm{path}},{l_0}}'$ under the standard atmospheric model. Due to the different nature of atmospheric transmittance and path radiation, linear correction of atmospheric transmittance and path radiation, at the same time, has opposite effect on infrared radiation measurement results of targets. Previous experiments have proved that it is even more important to improve the measurement accuracy of atmospheric transmittance when measuring long distant targets. Therefore, LAC factor can be obtained as follows:$$c_{\tau {{\rm{atm}},{\rm{LAC}}}} = \frac{{{\tau _{{\rm{atm}},{l_0}}}}}{{\tau _{{\rm{atm}},{l_0}}'}}$$ (10) According to the quantitative relation of distance, LEAC factor can be obtained[12]:
$$c_{\tau{{\rm{atm}},{\rm{LEAC}}}} = {0.99^{[{{\log }_2}(l/{l_0}) + 0.5]}} \times c_{\tau{{\rm{atm}},{\rm{LAC}}}}$$ (11) For any distance
$l$ , the theoretical atmospheric transmittance and path radiation obtained from MODTRAN are$\tau _{{\rm{atm}},l}'$ and$L_{{\rm{path}},l}'$ , respectively. The corrective atmospheric transmittance can be calculated at the distance$l$ by LAC factor or LEAC factor:$${\tau _{{\rm{atm}},l}} = c_{\tau {{\rm{atm}},{\rm{LAC}}}} \cdot \tau _{{\rm{atm}},l}'$$ (12) $${\tau _{{\rm{atm}},l}} = c_{\tau {{\rm{atm}},{\rm{LEAC}}}} \cdot \tau _{{\rm{atm}},l}'$$ (13) -
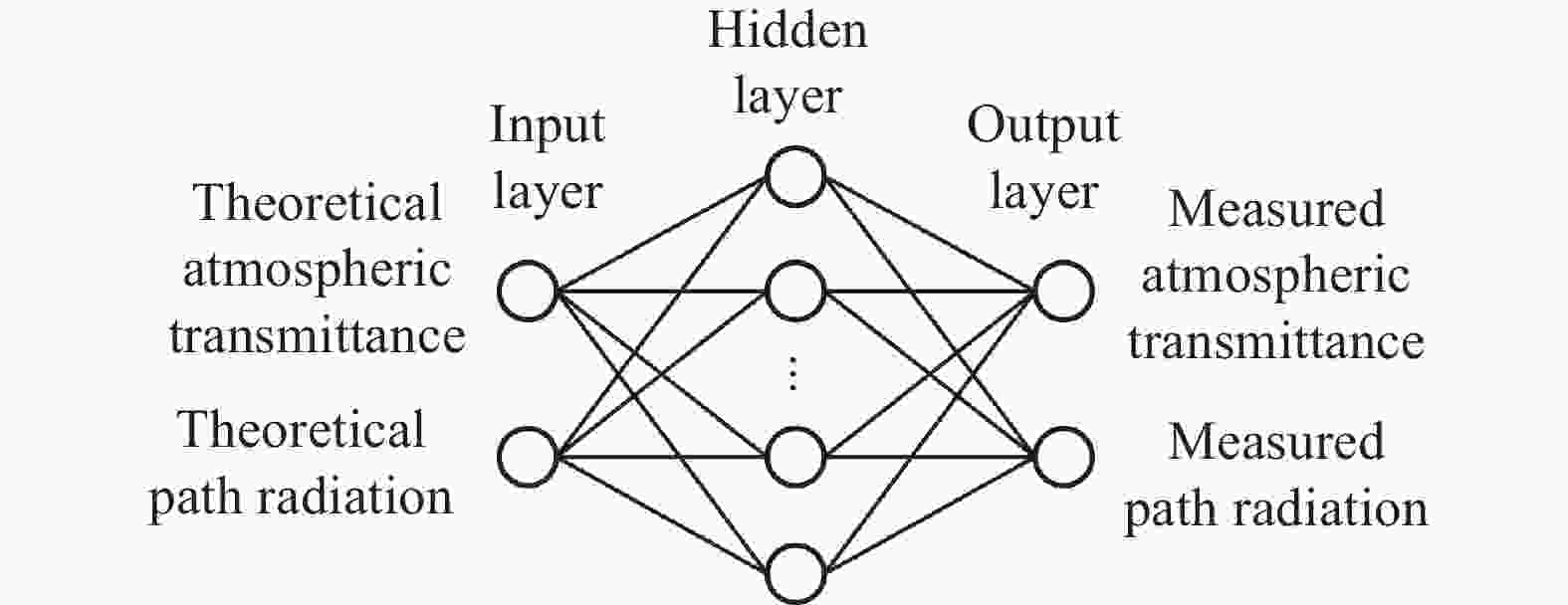
The neural network is a gradient descent back-propagation algorithm, which permits the solution of regression problems by estimating a transfer function from a set of known situations. It constitutes the priori information which is necessary for solution of the problem[13]. The database that is used to train the network is built from the measured atmospheric transmittance and path radiation related to the radiation transfer model of MODTRAN4.0. In other words, the input layer is the theoretical atmospheric transmittance and path radiation obtained from MODTRAN4.0 at different distances
$({l_1},{l_2},{l_3} \ldots )$ . And the output layer is the measured atmospheric transmittance and path radiation calculated by NRsrM at the corresponding distances. A three-layer neural network structure is established as shown in Fig. 4.For atmospheric transmittance and path radiation at arbitrary distances
$l$ , the constructed neural network can be used to predict the network output values by inputting theoretical values. -
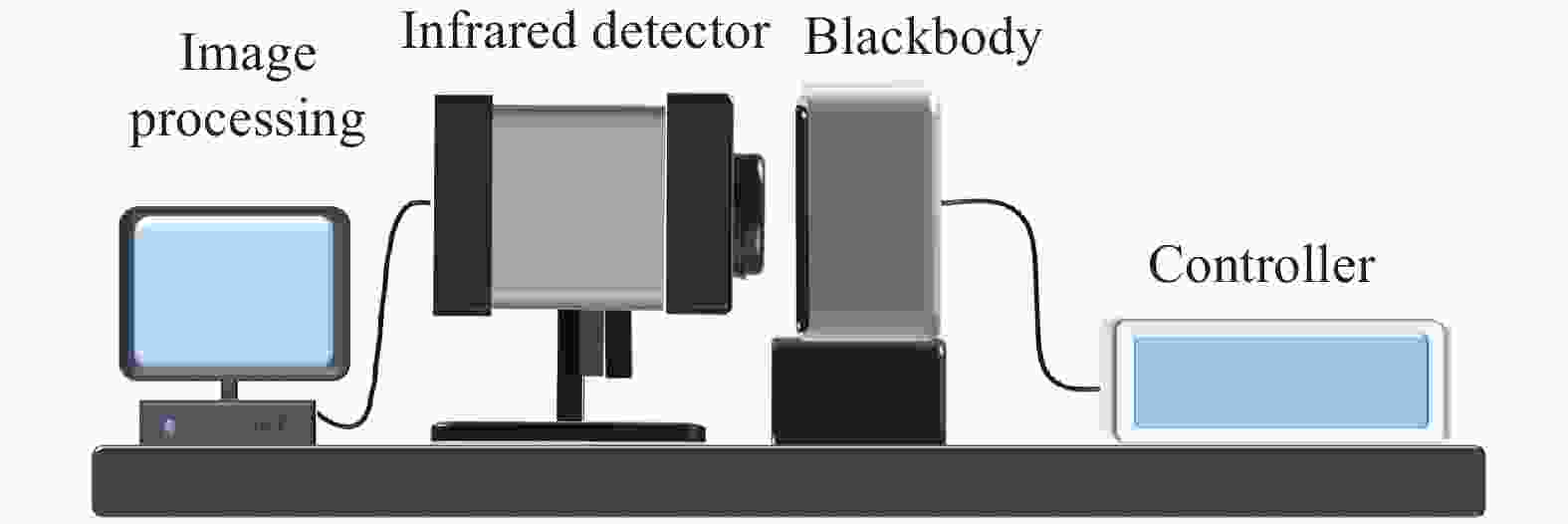
To verify the feasibility of this method, experiments were performed with a long-wave infrared (LWIR) camera of forward looking infrared (FLIR) systems. The infrared detector operates in the 7.7-9.3 μm waveband, and it is composed of 320 pixel×256 pixel with a 14-bit digital output. The extended area blackbody selected as the reference source has a 100 mm×100 mm size and exhibits high effective emissivity (0.97 in the 7.7-9.3 μm waveband). Its temperature accuracy is 0.01 ℃ over an operating temperature range of 0-125 ℃.
-
The experimental setup used for radiometric calibration based on the calibration principle shown in Fig. 2 is sketched in Fig. 5. The relationship between the gray value and the radiation brightness of the blackbody shows a linear characteristic, when the integration time of the infrared system is constant, as described above. Corresponding radiance can be calculated by Planck’s formula integral as the temperatures of the blackbody are set from 35 ℃ to 65 ℃ with an interval of 5 ℃. The gray value of the blackbody can be obtained from infrared imaging system. The result is shown in Fig. 6. The calibration equation can be fitted as
$$G = 268.9876 \times L(T) + 3194.2214$$ (14) It can be known that the response
$K$ of infrared measurement system is 268.987 6${\rm{DN/W}} \cdot {{\rm{m}}^{ - 2}} \cdot {\rm{s{r}}^{ - 1}}$ and the offset$B$ of infrared measurement system is 3194.2214${\rm{DN}}$ . -
In the conventional radiometric method, the atmospheric transmittance and path radiation are calculated by MODTRAN4.0. During the experiment, the ground average temperature is about 10 ℃; the pressure is about 1 021 kPa ; the relative humidity is about 20%; the angle of pitch is 0°; the altitude is 210 m and the visibility is about 9.7 km. The theoretical average atmospheric transmittance and path radiation in waveband 7.7-9.3 μm at the distance of 10 m to 100 m with the interval of 10 m are shown by the black line in Fig. 7, which are obtained from MODTRAN4.0 using the above measured parameters.
In order to obtain the LAC factor and LEAC factor, NRsrM is carried out to calculate the actual atmospheric transmittance and path radiation. The blackbody as a standard reference source is placed at a distance of
${l_0}$ =10 m from the infrared system. The gray value${G_l}$ and${G_h}$ of the black body infrared image are 9149${\rm{DN}}$ and 10132${\rm{DN}}$ at the temperature of 50 ℃ and 60 ℃, respectively. Thus, the actual atmospheric transmittance and path radiation at the distance of 10 m can be calculated from Eq.(8)−(9) and Planck’s formula as follows.
Figure 7. Atmospheric correction result at different distances. (a) Atmospheric transmittance at different distances; (b) path radiation at different distances
$${\tau _{{\rm{atm}},{l_0}}} = 0.935\;3$$ (15) $${L_{{\rm{path}},{l_0}}} = 0.863\;3 {\rm{\;W}} \cdot {{\rm{m}}^{ - 2}} \cdot {\rm {s{r^{ - 1}}}}$$ (16) The theoretical atmospheric transmittance is 0.989 8 at the distance of 10 m obtained from MODTRAN4.0. Thus, the LAC factor calculated from Eq.(10) is
$c{\tau _{{\rm{atm}},{\rm{LAC}}}}$ =0.944 9. According to the LAC factor, the corrected atmospheric transmittance at each distance can be calculated from Eq.(12), shown by the green line in Fig. 7(a). The LEAC factor can be calculated from Eq.(11) and the corrected atmospheric transmittance can be calculated from Eq.(13), shown by the orange line in Fig.7(a).In order to achieve NLAC, multiple sets of experiments are carried out at the distance of 10 to 100 m with an interval of 10 m, which adopt the NRsrM. The measured atmospheric transmittance and path radiation at each distance can be calculated from Eq.(8) and (9), shown by the blue line in Fig.7. Interpolation method is used to process 10 sets of measured data into 19 sets, which are distributed between 10 m and 100 m with the interval of 5 m. The database contained theoretical data at corresponding distances obtained from MODTRAN4.0 as an input layer and 19 sets of measured data as an output layer are used to train the network with the use of the constructed neural network in Fig.4. The network output value of the atmospheric transmittance and path radiation at each distance after training are shown by the red line in Fig.7.
-
In order to verify the improvement of infrared radiation measurement accuracy, images of the blackbody as an infrared target are collected at the distance of 130 m as shown in Fig.8. The theoretical atmospheric transmittance and path radiation obtained from MODTRAN4.0 are 0.918 8 and 0.812 1
${\rm{W}} \cdot {{\rm{m}}^{ - 2}} \cdot {\rm{s{r^{ - 1}}}}$ , respectively. The corrected atmospheric transmittance calculated by the LAC factor and LEAC factor are 0.868 1 and 0.832 2, respectively. The atmospheric transmittance and the path radiation predicted by NLAC of the constructed neural network are 0.694 7 and 3.917 2${\rm{W}} \cdot {{\rm{m}}^{ - 2}} \cdot {\rm{s{r^{ - 1}}}}$ , respectively. The temperatures of the target are from 40 ℃ to 80 ℃ with the interval of 10 ℃. The inversion results of radiation measurements calculated from Eq.(5) at different temperatures are shown in Fig.9.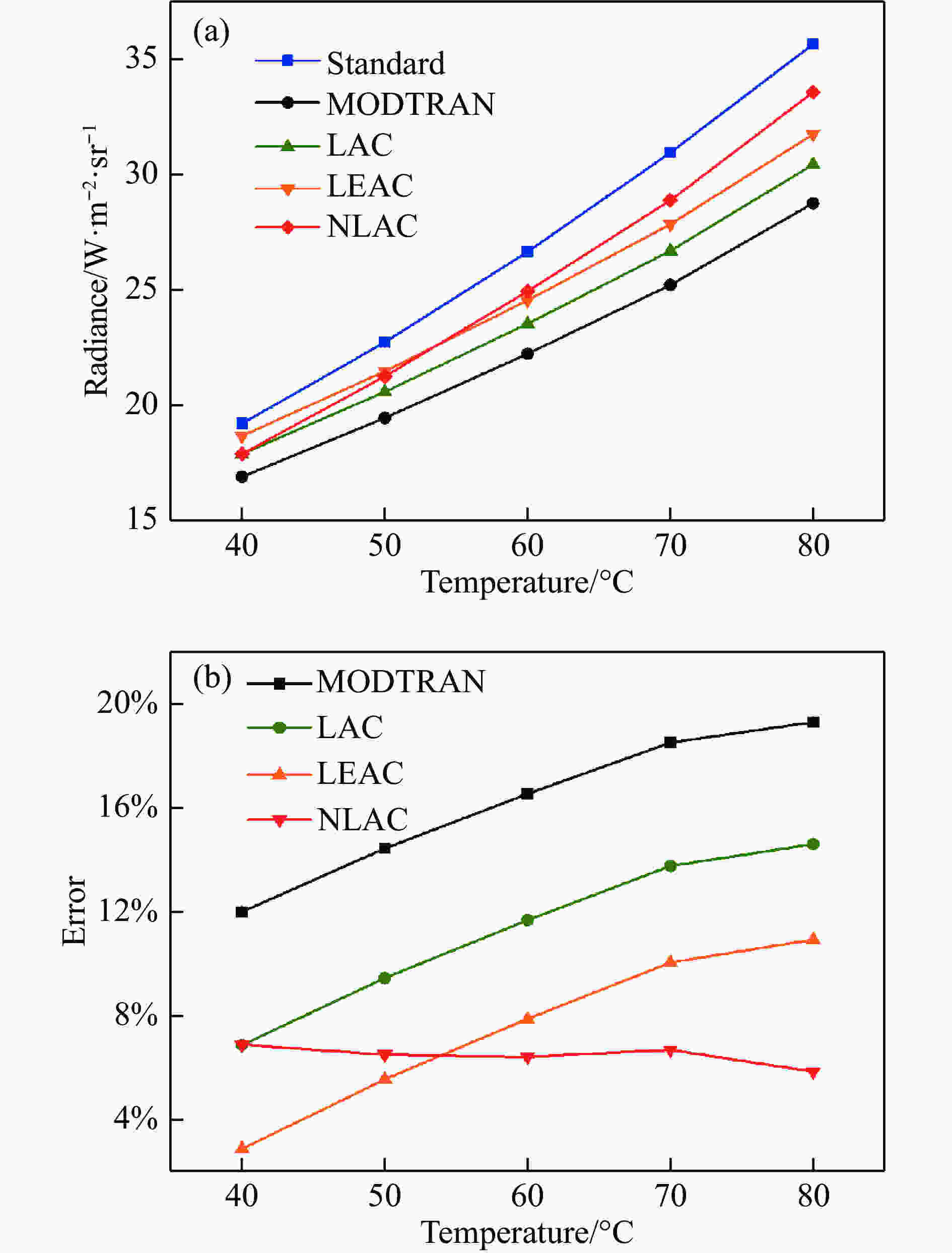
Figure 9. Radiometric result. (a) Inversion of radiation brightness result with the use of different methods; (b) Radiometric error with the use of different methods
As can be seen from the error curve, the errors of LAC and LEAC are smaller than MODTRAN, and the error trend is the same. The reason for this result is that they only make a simple linear correction for atmospheric transmittance. NLAC method modifies atmospheric transmittance and path radiation by near-rang measurement. Its error is relatively stable and the error size is mainly determined by the neural network algorithm. At 40 ℃, the error of LEAC is less than NLAC. The reason is that the relative error of 40 ℃ is less affected by the uncorrected path radiation, and it would be better just to correct the transmittance. NLAC method introduces the error of the path radiation correction. When the temperature is higher than 40 ℃, the influence of uncorrected path radiation gradually increases and the advantages of NLAC method are reflected. The maximum error and the average error of MODTRAN4.0, LAC, LEAC and NLAC are all listed in Tab. 1. The method of NLAC shows both lowest maximum error and average error. In summary, the method proposed in this paper, yielding high accuracy of radiometry, is valid for the infrared measurement system.
Table 1. Radiometric error of different methods
Error MODTRAN4.0 LAC LEAC NLAC Maximum error 19.32% 14.61% 10.92% 6.87% Average error 16.17% 11.27% 7.44% 6.45% -
This paper presents a method to improve the infrared radiometric accuracy based on atmospheric correction. Compared with the conventional radiometric method, near-range atmospheric transmittance and path radiation can be calculated simultaneously by NRsrM. Using NLAC of neural network technology, long-range atmospheric transmittance and path radiation are relatively accurately predicted through the nonlinear relationship between theoretical data obtained from MODTRAN4.0 and actual data calculated by NRsrM. Therefore, atmospheric correction is achieved to improve the infrared radiometric accuracy. Preliminary experiments have shown that the infrared radiometric average errors of the conventional method, LAC, LEAC and the proposed NLAC method are 16.17%, 11.27%, 7.44% and 6.45%, respectively. The infrared radiometric accuracy of LAC (or LEAC) method is improved compared with the conventional software calculation method. And it requires only a set of near-range measurement parameters by NRsrM, which is simple and easy to be obtained. Through NLAC of neural network, multiple sets of actual measurement results are needed. The process of atmosphere correction is more complicated before the target measurement, but the infrared radiometric accuracy can be further improved.
Nonlinear atmospheric correction based on neural network for infrared target radiometry
-
摘要:
红外辐射测量技术是表征目标红外特征的重要手段,而大气修正是获得目标真实辐射的必要步骤。提出了一种提高远距离目标红外辐射测量精度的非线性大气修正(NLAC)方法。该方法利用近距离标准参考源测量(NRSRM)来计算实时环境中不同位置的实际大气透过率和程辐射。相应条件下的理论大气透过率和程辐射也可以从大气辐射传输软件中获得。应用神经网络技术对两者之间的非线性关系进行拟合。因此,可以预测远距离的大气透过率和程辐射,以实现大气修正。为了进行比较,还进行了简单的线性大气修正(LAC)与线性增强大气修正(LEAC)。实验结果表明,该方法的红外辐射测量平均误差为6.45%,远低于常规方法,线性大气修正方法和线性增强大气修正,分别为16.17%,11.27%和7.44%。
Abstract:Infrared radiometry technology is an important means to characterize the infrared signature of targets, and atmospheric correction is a requisite step to obtain the real radiance of targets. A nonlinear atmospheric correction (NLAC) method was proposed to improve the infrared radiometric accuracy for long distance targets in this paper. This method used near-range standard reference source measurement (NRSRM) to calculate the actual atmospheric transmittance and path radiation simultaneously at different locations in a real-time environment. And the theoretical atmospheric transmission and path radiation under the corresponding conditions could be obtained from the atmospheric radiation transmission software as well. Neural network technology was applied to fit the non-linear relationship between them. Thus, the atmospheric transmittance and path radiation over long distances could be predicted to achieve atmospheric correction. Simpler linear atmospheric correction (LAC) and linear enhancement atmospheric correction (LEAC) were also carried out for comparison. The experimental results indicate that the infrared radiometric average error of the proposed method is 6.45%, which is much lower than that of the conventional method, LAC and LEAC that are 16.17%, 11.27% and 7.44%, respectively.
-
Table 1. Radiometric error of different methods
Error MODTRAN4.0 LAC LEAC NLAC Maximum error 19.32% 14.61% 10.92% 6.87% Average error 16.17% 11.27% 7.44% 6.45% -
[1] Cai L-H, He F-Y, Chang S-T, et al. A wide dynamic range NUC algorithm for IRCS systems [J]. Journal of the Korean Physical Society, 2018, 73(12): 1821−1826. doi: 10.3938/jkps.73.1821 [2] Xue X, Liu C, Qiao J, et al. The research about radiometric technology of two-dimensional rotary table based on image gray level [J]. EURASIP Journal on Image and Video Processing, 2019, 2019(1). [3] Ata Y, Nakiboğlu K C. IR signature estimation of an object or a target by taking into account atmospheric effects [J]. Optics Communications, 2010, 283(20): 3901−3910. doi: 10.1016/j.optcom.2010.06.006 [4] Cai L H, Li Z, Yu Y, et al. Direct atmospheric correction for high precision radiometry on infrared small target [J]. Infrared and Laser Engineering, 2018, 47(S1): S104002. [5] Wei H L, Chen X H, Rao R Z, et al. A moderate-spectral-resolution transmittance model based on fitting the line-by-line calculation [J]. Optics Express, 2007, 15(13): 8360. doi: 10.1364/OE.15.008360 [6] Huang Z, Yin L, Wang J, et al. Atmospheric attenuation correction based on a constant reference for high-precision infrared radiometry [J]. Applied Sciences, 2017, 7(11): 1165. doi: 10.3390/app7111165 [7] Tardy B, Rivalland V, Huc M, et al. A software tool for atmospheric correction and surface temperature estimation of landsat infrared thermal data [J]. Remote Sensing, 2016, 8(9): 696. doi: 10.3390/rs8090696 [8] Dumoulin J, Boucher V. Infrared thermography system for transport infrastructures survey with inline local atmospheric parameter measurements and offline model for radiation attenuation evaluations [J]. Journal of Applied Remote Sensing, 2014, 8(1): 084978. doi: 10.1117/1.JRS.8.084978 [9] Mermelstein M D, Snail K A, Priest R G. Spectral and radiometric calibration of midwave and longwave infrared cameras [J]. Optical Engineering, 2000, 39(39): 574−579. [10] Chang S, Zhang Y, Sun Z, et al. Method to remove the effect of ambient temperature on radiometric calibration [J]. Appl Opt, 2014, 53(27): 6274−6279. doi: 10.1364/AO.53.006274 [11] Anderson G P, Berk A, Acharya P K, et al. MODTRAN4: multiple scattering and bidirectional reflectance distribution function (BRDF) upgrades to MODTRAN [C]//SPIE, 2000, 4049:176–183. [12] Guo L H, Guo H Z, Yang C Y, et al. Improvement of radiation measurement precision for target by using atmosphere corrected coefficients [J]. Optics and Precision Engineering, 2016, 24(8): 1871−1877. doi: 10.3788/OPE.20162408.1871 [13] Cathy C, Juliette H L, Sébastien P, et al. Retrieval of CO from nadir remote-sensing measurements in the infrared by use of four different inversion algorithms [J]. Appl Opt, 2002, 41(33): 7068−7078. doi: 10.1364/AO.41.007068 -
 点击查看大图
点击查看大图
计量
- 文章访问数: 886
- HTML全文浏览量: 566
- 被引次数: 0






 下载:
下载: