下载:
-
红外成像技术是当今迅速发展的高新技术之一，其通过探测目标与背景的红外辐射强度差异，来实现对目标的发现、识别和跟踪。但随着光电对抗技术的发展，研究人员常采用改变或者降低目标材质表面的红外辐射特性，通过降低目标材质与背景及周围环境的辐射差异来影响目标材质红外探测识别的正确率。目前，改变材质表面辐射特性的常用方法主要为控制目标材质表面发射率[1- 2]，通过在目标材质表面涂覆不同发射率的涂层来改变材质表面的辐射特性，以达到改变材质表面辐射特性、改变目标材质的热辐射轮廓等目的，严重降低了通过红外识别检测目标材质的正确率。美国是较早开展通过涂料实现红外隐身的国家，20世纪70年代末至80年代初，美国地面装备红外隐身涂料研制工作己初见成效，提出了一种根据涂料配方及其原材料参数预测其红外辐射特性的模拟计算方法，并对红外隐身涂料的配方设计提出了一些重要结论[3]。80年代中叶，西方各国纷纷介入红外隐身涂料研究，其中澳大利亚国防部材料研究室发表的一篇红外隐身涂料的研制报告引起广泛关注。美国最近有专利提出一种由多层颜料粒子组成的能透射射频、反射红外的涂料或薄膜的制备方法。
文中主要针对由材质表面发射率改变引起的目标材质识别正确率降低的问题来展开研究工作，利用不同物体或同一物体的不同状态在热红外波段往往具有不同的偏振状态的特点，文中首先基于红外辐射偏振传输模型研究分析了材质表面发射率对红外线偏振度特性的影响；其次，通过开展相同基底材质在不同发射率涂层条件下的红外高光谱偏振成像试验，研究分析了发射率改变对目标材质表面红外光谱偏振特性的影响；最后，在理论分析和试验验证的基础上，提出了基于红外光谱偏振度对比度特征的涂层材质探测识别方法。研究成果对于通过改变表面发射率的红外伪装材质探测识别的深入研究具有指导意义。
-
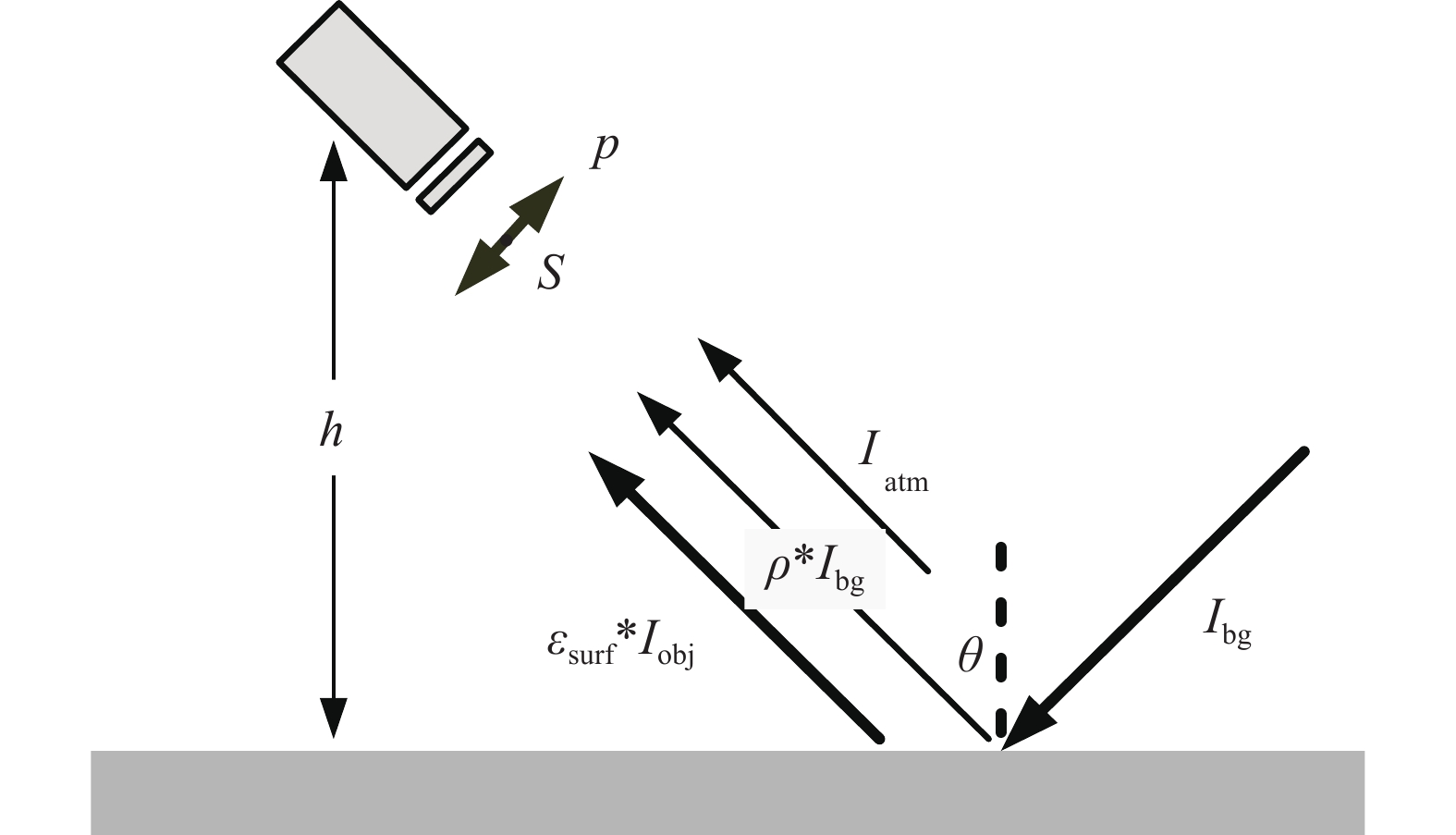
对于不透明的辐射目标材质，其表面的发射辐射主要由背景反射和自身辐射组成。图1为红外辐射偏振传输模型示意图。
图 1 红外辐射偏振传输模型示意图
Figure 1. Radiation transmission model of infrared polarization
假设入射到偏振器件前的Stokes矢量记为
${{{S}}^{\rm in}}$ ，经过偏振器件后的Stokes矢量记为${{{S}}^{\rm out}}$ ，则对于红外偏振成像系统，两者之间存在线性的转换关系，如下式：$${{{S}}^{\rm out}} = {{M}} \cdot {{{S}}^{\rm in}}$$ (1) 式中：
${{M}}$ 表示偏振器件的穆勒矩阵。在红外偏振成像实验中，通过偏振成像系统获取并计算得出的Stokes矢量就是所谓的${{{S}}^{\rm in}}$ ，即红外偏振辐射传输方程的Stokes表达式。由图1可知：场景表面的Stokes矢量${{{S}}^{\rm in}}$ 可表示为对太阳及天空背景的反射Stokes矢量${{{S}}^{\rm{r}}}$ 与其自身发射辐射Stokes矢量${{{S}}^{\rm{e}}}$ 之和，即${{{S}}^{\rm in}} = {{{S}}^r} + {{{S}}^{\rm{e}}}$ 。根据红外辐射偏振传输模型可知，对于不透明的辐射物体，入射到红外线栅偏振片前的Stokes矢量
${{{S}}^{\rm in}}$ 可表示为：$${{{S}}^{\rm in}} = {{{S}}^{\rm{r}}} + {{{S}}^{\rm{e}}} = \int {{{f}}({\theta _{\rm{i}}},{\phi _{\rm{i}}},{\theta _{\rm{r}}},{\phi _{\rm{r}}},\lambda )} \cos ({\theta _{\rm{r}}}){\rm{d}}{\varOmega _{\rm{r}}} \cdot {{{S}}^{\rm{i}}} + {{\bf{\varepsilon }}_{\rm surf}} \cdot {I_{\rm obj}}$$ (2) 式中：
${{{S}}^{\rm{i}}}$ 为入射光Stokes矢量；${I_{\rm obj}}$ 为目标的辐射强度；${{f}}$ 为基于微面元理论的Priest-Germer模型；${\rm{d}}{\varOmega _{\rm{r}}} = \sin {\theta _{\rm{r}}}{\rm{d}}{\theta _{\rm{r}}}{\rm{d}}{\phi _{\rm{r}}}$ ；用菲涅耳反射穆勒矩阵及基于微面元理论的BRDF模型来表示入射辐射到反射辐射的传输关系，根据入射界面的Stokes矢量${{{S}}^{\rm{i}}}$ ，可得反射的Stokes矢量${{{S}}^{\rm{r}}}$ 可表示为[3]：$$\left( {\begin{aligned} {S_0^{\rm{r}}} \\ {S_1^{\rm{r}}} \\ {S_2^{\rm{r}}} \\ {S_3^{\rm{r}}} \end{aligned}} \right) = \left( {\begin{array}{*{20}{c}} {\int {{f_{00}}\cos {\theta_{\rm{r}}}{\rm{d}}{\varOmega_{\rm{r}}}} }&{\int {{f_{01}}\cos {\theta_{\rm{r}}}{\rm{d}}{\varOmega_{\rm{r}}}} }&{\int {{f_{02}}\cos {\theta_{\rm{r}}}{\rm{d}}{\varOmega_{\rm{r}}}} }&{\int {{f_{03}}\cos {\theta_{\rm{r}}}{\rm{d}}{\varOmega_{\rm{r}}}} } \\ {\int {{f_{10}}\cos {\theta_{\rm{r}}}{\rm{d}}{\varOmega_{\rm{r}}}} }&{\int {{f_{11}}\cos {\theta_{\rm{r}}}{\rm{d}}{\varOmega_{\rm{r}}}} }&{\int {{f_{12}}\cos {\theta_{\rm{r}}}{\rm{d}}{\varOmega_{\rm{r}}}} }&{\int {{f_{13}}\cos {\theta_{\rm{r}}}{\rm{d}}{\varOmega_{\rm{r}}}} } \\ {\int {{f_{20}}\cos {\theta_{\rm{r}}}{\rm{d}}{\varOmega_{\rm{r}}}} }&{\int {{f_{21}}\cos {\theta_{\rm{r}}}{\rm{d}}{\varOmega_{\rm{r}}}} }&{\int {{f_{22}}\cos {\theta_{\rm{r}}}{\rm{d}}{\varOmega_{\rm{r}}}} }&{\int {{f_{23}}\cos {\theta_{\rm{r}}}{\rm{d}}{\varOmega_{\rm{r}}}} } \\ {\int {{f_{30}}\cos {\theta_{\rm{r}}}{\rm{d}}{\varOmega_{\rm{r}}}} }&{\int {{f_{31}}\cos {\theta_{\rm{r}}}{\rm{d}}{\varOmega_{\rm{r}}}} }&{\int {{f_{32}}\cos {\theta_{\rm{r}}}{\rm{d}}{\varOmega_{\rm{r}}}} }&{\int {{f_{33}}\cos {\theta_{\rm{r}}}{\rm{d}}{\varOmega_{\rm{r}}}} } \end{array}} \right)\left( {\begin{aligned} {S_0^i} \\ {S_1^i} \\ {S_2^i} \\ {S_3^i} \end{aligned}} \right)$$ (3) 对于不透明的辐射目标表面，通常红外偏振成像接收的辐射包括场景的辐射和对其他辐射源的反射，则目标表面总的辐射亮度可以表示为：
$$\begin{split}{{{L}}_{\rm tol}} = \;& {{{L}}_{\rm{e}}} + {{{L}}_{\rm{r}}} = {L_{\rm{B}}} \cdot {{{\varepsilon }}_{\rm surf}} +\\ & \int {{{f}}\left( {{\theta_{\rm{i}}},{\phi_{\rm{i}}},{\theta_{\rm{r}}},{\phi_{\rm{r}}},\lambda } \right)} \cdot {{L}}\left( {{\theta_{\rm{i}}},{\phi_{\rm{i}}}\lambda } \right)\cos \left( {{\theta_{\rm{i}}}} \right){\rm{d}}{\varOmega_{\rm{i}}}\end{split}$$ (4) 为了计算目标表面辐射率，需要引入局部热量动态平衡的概念[4]。局部动态平衡首先假设参与辐射和吸收过程中的原子和分子数量可以通过平衡值给出。注意：此处的假设平衡是指材料的不同状态，而不是材料本身与周围环境的平衡。由于入射辐射是与表面同温度的热辐射，故总辐射就是相同温度下的黑体辐射，即：
$${L_{\rm{B}}} \cdot {{\bf{\varepsilon }}_0} = {L_{\rm{B}}} \cdot {{\bf{\varepsilon }}_{\rm surf}} + \int {{f}} \left( {{\theta _{\rm{i}}},{\phi _{\rm{i}}},{\theta _{\rm{r}}},{\phi _{\rm{r}}},\lambda } \right) \times {L_{\rm{B}}} \cdot {{\bf{\varepsilon }}_0}\cos \left( {{\theta _{\rm{i}}}} \right){\rm{d}}{\varOmega _{\rm i}}$$ (5) 式中：
${L_B}$ 为黑体辐射亮度。由公式(5)可得出目标材质表面的偏振辐射发射率的表达式：$$\begin{split} {{\bf{\varepsilon }}_{\rm surf}} \; &= \left[ {1 - \int {{\bf{f}}({\theta_{\rm{i}}},{\phi _{\rm{i}}},{\theta_{\rm{r}}},{\phi_{\rm{r}}},\lambda )\cos ({\theta_{\rm{i}}}){\rm{d}}{\varOmega_{\rm{i}}}} } \right] \cdot {{\bf{\varepsilon }}_0} \\ & = \left[ {\begin{array}{*{20}{c}} {1 - \int {{f_{00}}({\theta_{\rm{i}}},{\phi _{\rm{i}}},{\theta_{\rm{r}}},{\phi_{\rm{r}}},\lambda )\cos ({\theta_{\rm{i}}}){\rm{d}}{\varOmega_{\rm{i}}}} } \\ { - \int {{f_{10}}({\theta_{\rm{i}}},{\phi _{\rm{i}}},{\theta_{\rm{r}}},{\phi_{\rm{r}}},\lambda )\cos ({\theta_{\rm{i}}}){\rm{d}}{\varOmega_{\rm{i}}}} } \\ { - \int {{f_{20}}({\theta_{\rm{i}}},{\phi _{\rm{i}}},{\theta_{\rm{r}}},{\phi_{\rm{r}}},\lambda )} \cos ({\theta_{\rm{i}}}){\rm{d}}{\varOmega_{\rm{i}}}} \\ { - \int {{f_{30}}({\theta_{\rm{i}}},{\phi _{\rm{i}}},{\theta_{\rm{r}}},{\phi_{\rm{r}}},\lambda )\cos ({\theta_{\rm{i}}}){\rm{d}}{\varOmega_{\rm{i}}}} } \end{array}} \right] \\ & = \left[ {\begin{array}{*{20}{c}} {1 - \int {{f_{00}}({\theta_{\rm{i}}},{\phi _{\rm{i}}},{\theta_{\rm{r}}},{\phi_{\rm{r}}},\lambda )\cos ({\theta_{\rm{r}}}){\rm{d}}{\varOmega_{\rm{r}}}} } \\ { - \int {{f_{10}}({\theta_{\rm{i}}},{\phi _{\rm{i}}},{\theta_{\rm{r}}},{\phi_{\rm{r}}},\lambda )\cos ({\theta_{\rm{r}}}){\rm{d}}{\varOmega_{\rm{r}}}} } \\ { - \int {{f_{20}}({\theta_{\rm{i}}},{\phi _{\rm{i}}},{\theta_{\rm{r}}},{\phi_{\rm{r}}},\lambda )\cos ({\theta_{\rm{r}}}){\rm{d}}{\varOmega_{\rm{r}}}} } \\ { - \int {{f_{30}}({\theta_{\rm{i}}},{\phi _{\rm{i}}},{\theta_{\rm{r}}},{\phi_{\rm{r}}},\lambda )\cos ({\theta_{\rm{r}}}){\rm{d}}{\varOmega_{\rm{r}}}} } \end{array}} \right] \end{split} $$ (6) 由此可知，目标材质表面自身辐射的Stokes矢量
${{{S}}^{\rm{e}}}$ 可以表示为：${{{S}}^{\rm{e}}} = {{\bf{\varepsilon }}_{{\rm{surf}}}} \cdot {I_{\rm obj}}$ 。其中，${I_{\rm obj}}$ 为目标的辐射强度。则公式(2)可表示为：$${{{S}}^{\rm in}} = \left[ {\begin{aligned} I \\ Q \\ U \\ V \end{aligned}} \right] = \left[ {\begin{array}{*{20}{c}} {{I_{\rm{obj}}} + \int {{f_{00}}({\theta_{\rm{i}}},{\phi_{\rm{i}}},{\theta_{\rm{r}}},{\phi_{\rm{r}}},\lambda )\cos ({\theta_{\rm{r}}}){\rm{d}}{\varOmega_{\rm{r}}}({I_{\rm{bg}}} - {I_{\rm{obj}}})} } \\ {\int {{f_{10}}({\theta_{\rm{i}}},{\phi_{\rm{i}}},{\theta_{\rm{r}}},{\phi_{\rm{r}}},\lambda )\cos ({\theta_{\rm{r}}}){\rm{d}}{\varOmega_{\rm{r}}}({I_{\rm{bg}}} - {I_{\rm{obj}}})} } \\ {\int {{f_{20}}({\theta_{\rm{i}}},{\phi_{\rm{i}}},{\theta_{\rm{r}}},{\phi_{\rm{r}}},\lambda )\cos ({\theta_{\rm{r}}}){\rm{d}}{\varOmega_{\rm{r}}}({I_{\rm{bg}}} - {I_{\rm{obj}}})} } \\ {\int {{f_{30}}({\theta_{\rm{i}}},{\phi_{\rm{i}}},{\theta_{\rm{r}}},{\phi_{\rm{r}}},\lambda )\cos ({\theta_{\rm{r}}}){\rm{d}}{\varOmega_{\rm{r}}}({I_{\rm{bg}}} - {I_{\rm{obj}}})} } \end{array}} \right]$$ (7) 由上式可知，场景表面的Stokes矢量
${{{S}}^{\rm in}}$ 与${f_{00}}$ 、${f_{10}}$ 、${f_{20}}$ 密切相关，${f_{00}}$ 、${f_{10}}$ 、${f_{20}}$ 可由菲涅耳反射穆勒矩阵${{M}}({\theta _{\rm{i}}},{\phi _{\rm{i}}},{\theta _{\rm{r}}},{\phi _{\rm{r}}})$ 中的${m_{00}}$ 、${m_{10}}$ 、${m_{20}}$ 计算得出(由于红外辐射偏振Stokes参量V很小，在计算中通常忽略V参数，故此处略去${m_{30}}$ 的求解计算)，将${m_{00}}$ 、${m_{10}}$ 、${m_{20}}$ 代入公式(7)可得：$$\left(\begin{aligned} I \\ Q \\ U \\ V \end{aligned}\right) = \left[\begin{array}{*{20}{c}} {{I_{\rm{obj}}} + \dfrac{1}{{8{\text{π}}{\sigma ^2}}}\int {\dfrac{1}{{{{\cos }^4}\theta }}\dfrac{{\exp ( - ({{\tan }^2}\theta /2{\sigma ^2}))}}{{\cos ({\theta_{\rm{i}}})}}({R_{\rm{s}}} + {R_{\rm{p}}}){\rm{d}}{\varOmega_{\rm{r}}}({I_{\rm{bg}}} - {I_{\rm{obj}}})} } \\ {\dfrac{1}{{8{\text{π}}{\sigma ^2}}}\int {\dfrac{1}{{{{\cos }^4}\theta }}\dfrac{{\exp ( - ({{\tan }^2}\theta /2{\sigma ^2}))}}{{\cos ({\theta_{\rm{i}}})}}\cos (2{\eta_{\rm{i}}})({R_{\rm{s}}} - {R_{\rm{p}}}){\rm{d}}{\varOmega_{\rm{r}}}({I_{\rm{bg}}} - {I_{\rm{obj}}})} } \\ {\dfrac{1}{{8{\text{π}}{\sigma ^2}}}\int {\dfrac{1}{{{{\cos }^4}\theta }}\dfrac{{\exp ( - ({{\tan }^2}\theta /2{\sigma ^2}))}}{{\cos ({\theta_{\rm{i}}})}}\sin (2{\eta_{\rm{i}}})({R_{\rm{p}}} - {R_{\rm{s}}})}{\rm{d}}{\varOmega_{\rm{r}}}({I_{\rm{bg}}} - {I_{\rm{obj}}})}\\ 0 \end{array}\right]$$ (8) 故通过
${m_{00}}$ 、${m_{10}}$ 、${m_{20}}$ 推导得出的Stokes各参量完全符合其物理定义。由此可知，目标的偏振状态与表面折射率、入射角、反射角、粗糙度等多种因素相关，同时也与目标背景的辐射强度密切相关。由公式(8)及偏振度定义可推导得出基于红外辐射偏振传输模型的偏振度计算表达式为：
$$\begin{split} p =\; & \dfrac{{\sqrt {{Q^2} + {U^2}} }}{I} = \dfrac{{\dfrac{1}{{8{\text{π}}{\sigma ^2}}}\left| {{I_{\rm bg}} - {I_{\rm obj}}} \right|}}{{{I_{\rm obj}} + \dfrac{1}{{8{\text{π}}{\sigma ^2}}}\int {\dfrac{1}{{{{\cos }^4}\theta }} \cdot \dfrac{{\exp ( - ({{\tan }^2}\theta /2{\sigma ^2}))}}{{\cos ({\theta _{\rm{i}}})}}({R_{\rm{s}}} + {R_{\rm{p}}}){\rm{d}}{\Omega _{\rm{r}}}({I_{\rm bg}} - {I_{\rm obj}})} }} \cdot \\ &\sqrt {{{[\int {\dfrac{1}{{{{\cos }^4}\theta }} \cdot \dfrac{{\exp ( - ({{\tan }^2}/2{\sigma ^2}))}}{{\cos ({\theta _{\rm{i}}})}}\cos (2{\eta _{\rm{i}}})({R_{\rm{s}}} - {R_{\rm{p}}}){\rm{d}}{\Omega _{\rm{r}}}} ]}^2} + {{[\int {\dfrac{1}{{{{\cos }^4}\theta }} \cdot \dfrac{{\exp ( - ({{\tan }^2}\theta /2{\sigma ^2}))}}{{\cos ({\theta _{\rm{i}}})}}} \sin (2{\eta _{\rm{i}}})({R_{\rm{p}}} - {R_{\rm{s}}}){\rm{d}}{\Omega _{\rm{r}}}]}^2}} \end{split} $$ (9) 式中：
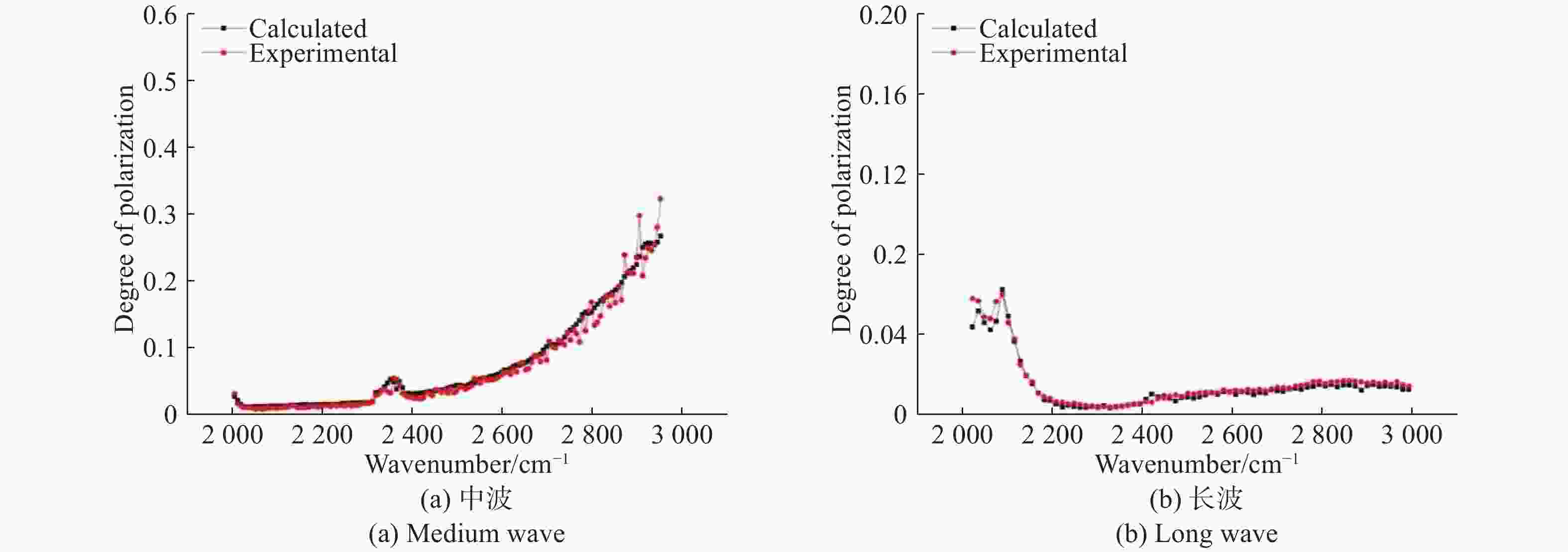
${R_{\rm{s}}}$ 、${R_{\rm{p}}}$ 为菲涅耳反射率的垂直和平行分量。由公式(9)可知，目标表面的红外辐射线偏振度特征与目标表面的折射率、粗糙度、入射角、探测角以及目标、背景的辐射强度等多种因素相关，尽管改变目标表面发射率可以改变目标表面的红外辐射特性，但由公式(8)可知，目标表面发射率降低时，目标表面辐射强度${I_{\rm obj}}$ 随之降低，红外线偏振度的计算公式中分子、分母随目标表面辐射强度变化的收敛性近似恒定，也就是说改变目标材质表面的发射率不影响目标表面的红外辐射偏振度。由上述红外辐射偏振传输模型的推导分析可知，红外高光谱偏振特性模型的单波段传输模型均可按基于微面元理论的红外辐射偏振传输模型进行推导分析。图2为某低发射率涂层材质在表面辐射温度为40 ℃的中、长波光谱偏振度实测与根据模型仿真计算结果的对比图。由图可知，在中、长波波段，模拟曲线和实测曲线的变化趋势基本一致，由涂层材质红外高光谱偏振度仿真与实测比较结果可知，基于微面元理论的红外高光谱偏振特性传输模型的仿真结果与材质表面的红外光谱偏振度实测值有较好的一致性(在中、长波波段，40 ℃的模拟值与实验值的平均误差分别为15.76%、12.36%)。
图 2 低发射率涂层材质在40 ℃时中、长波红外光谱偏振度模拟结果与测量结果对比图
Figure 2. Contrast curves of infrared spectural polarization degree of low emissivity coating materials at the temperature of 40 ℃
-
由前节基于红外辐射偏振传输模型的推导分析可知，改变目标材质表面的发射率不影响目标材质表面的红外辐射偏振度特征。考虑到由于不同涂层材质高光谱偏振精细结构方面的特征往往存在差异，本节主要通过红外涂层材质的红外高光谱偏振特性试验测试验证理论推导的正确性。另外，还提出可通过红外光谱偏振度对比度评价指标分析评价目标材质表面的光谱偏振特性差异。
-
描述光波偏振态的方法主要有两种[5]：（1）琼斯矢量表示法。通过琼斯矢量表示某电场矢量的x、y分量，其与电场的振幅及相位相关，在偏振光发生干涉效应时，通常选用琼斯矢量法计算，但琼斯矢量不能描述自然光和部分偏振光，当需要描述光的任意偏振态时，不适用琼斯矢量法。（2） Stokes矢量表示法，可描述完全偏振光、部分偏振光和完全非偏振光，其主要通过4个Stokes参量来描述光波的偏振态和强度，通用表达式为：
${{S}} = {(I,Q,U,V)^{\rm{T}}}$ ，参量I与入射光强有关；Q与0°和90°方向的线偏振信息有关；U与45°和135°方向的线偏振信息有关；V与左/右旋的圆偏振信息有关，通常自然目标的圆偏振分量很小，故可忽略不计。由于Stokes参量具有强度量纲，故在实际探测中，可直接通过探测器探测不同偏振方向的辐射强度图像来计算Stokes参量，即$${{S}} = \left[ {\begin{aligned} I \\ Q \\ U \\ V \end{aligned}} \right] = \left[ {\begin{array}{*{20}{l}} {{g_{{0^ \circ }}} + {g_{{{90}^ \circ }}}} \\ {{g_{{0^ \circ }}} - {g_{{{90}^ \circ }}}} \\ {{g_{{{45}^ \circ }}} - {g_{{{135}^ \circ }}}} \\ {{g_{\rm RCP}} - {g_{\rm LCP}}} \end{array}} \right]$$ (10) 式中：gθ (θ=0°，45°，90°，135°)为偏振片旋转θ时的热图像。
${g_{\rm RCP}}$ 和${g_{\rm LCP}}$ 分别表示右旋和左旋圆偏振。Stokes参量主要用来描述光束的偏振态，但不能完整描述目标景物反射及辐射的偏振态变化与其表面状态和固有属性的密切关系。通过实测试验数据计算偏振度的方法可由Stokes参量计算获得：$$p = \frac{{\sqrt {{Q^2} + {U^2}} }}{I}$$ (11) 由上式可知，偏振度表示从0到1的无量纲数，当p=0时，表示非偏振光；当p=1时，表示全偏振光；当0<p<1时，表示部分偏振光。则目标表面的不同波段的光谱偏振度可通过由测试数据计算获得的Stokes参量计算得出，由上节可知：目标表面的发射率改变不影响目标表面的红外偏振度特性，为了验证该结论，提出将红外光谱偏振度对比度作为评价指标，其计算表达式如下：
$${C_{p(\lambda )}} = \frac{{{P_\lambda }({T_{{\text{高}}}}) - {P_\lambda }({T_{{\text{低}}}})}}{{{P_\lambda }({T_{{\text{低}}}})}}$$ (12) 式中：
${P_\lambda }({T_{{\text{高}}}})$ 为目标表面辐射温度为${T_{{\text{高}}}}$ 时的红外光谱偏振度；${P_\lambda }({T_{{\text{低}}}})$ 为目标表面辐射温度为${T_{{\text{低}}}}$ 时的红外光谱偏振度。 -
为了验证理论分析结果的正确性，课题组开展了相同基底不同发射率的涂层材质的中波红外高光谱偏振成像试验，测试材质主要包括涂敷高发射率涂层材质-样板、低发射率涂层材质-样板，材质样板基底相同，表面涂层材质不同。试验中使用的FIRST中/长波红外高光谱成像仪采用傅立叶变换技术，在实现中波1.5~5 µm和长波8~11 µm高分辨率光谱探测同时，可实现320×256分辨率的空间成像。偏振器件为英国SPECAC公司BaF2的金属线栅偏振片为检偏器，BaF2在2~12 μm波段范围内均有高透过率(红外偏振测量精度通过标准黑体进行检测，优于0.05)。测试用黑体为本所自研，黑体温度可从室温加热至200 ℃，加热表面平整，通过将材质样板贴附到表面加热。测试实验环境温度约为20 ℃，红外高光谱成像仪与被测目标的距离约为10 m。图3为材质样板加热布置图，其中黑体材料1、2就是自研黑体的加热表面，表面发射率约为0.99。高发射率材料在中波波段的发射率为0.9，低发射率材料在中波波段的发射率为0.7。试验中加热从室温开始到80 ℃，每加热10 ℃完成测试一次。
图 3 材质样板加热装置及试验布置图
Figure 3. Material sample heating device and test layout plan
图4为不同发射率涂层材质在相同表面辐射温度条件下的无偏振中波红外辐射强度图像和对应的红外偏振度图像。由图可知，尽管材质表面辐射温度相同，但由于发射率不同，红外辐射强度有明显差别；而不同发射率材质在相同辐射温度条件下，其表面红外线偏振度图像则近乎相同。为了对涂层材质表面的光谱偏振特性进行验证分析，课题组还开展了高、低发射率涂层材质的红外高光谱偏振成像试验，材质通过自研黑体进行可控加热，使高、低发射率材质表面辐射温度相同。图5为相同基底的高、低发射率涂层材质在相差均为20 ℃的中波光谱辐射亮度及对应的光谱偏振度对比度比较图，图5(a)、(b)中纵坐标分别为红外光谱辐射亮度对比度、红外光谱偏振度对比度。由图可知：由于材质表面的发射率有差异，材质即使表面辐射温度相同，高、低发射率涂层材质表面辐射亮度对比度在探测波段范围内有明显差异，而光谱偏振度对比度在探测波段范围内没有规律性变化，且相对较稳定。由此可知，材质表面的光谱偏振特性与材质表面状态相关，改变涂层材质表面发射率不影响材质表面的光谱偏振特性。
图 4 不同涂层材质在相同辐射温度条件下的中波红外辐射强度图像和红外线偏振度图像
Figure 4. Mid-wave infrared radiation image and mid-wave infrared linear polarization degree image of different coating materials at the same temperature
图 5 相同基底的高、低发射率涂层材质光谱辐射亮度对比度及光谱偏振度对比度曲线图
Figure 5. Contrast curves of spectral radiation brightness and spectral polarization of high and low emissivity coatings with the same substrate
试验数据结果表明：当同一材质涂覆发射率不同的涂料，尽管辐射值发生明显的变化，但其偏振度并没有因为辐射率的改变而发生较大变化。也就是说，通过改变红外涂层材质表面发射率的方法可以改变材质表面的红外辐射特征，但其表面红外光谱偏振度并不会发生大的变化。
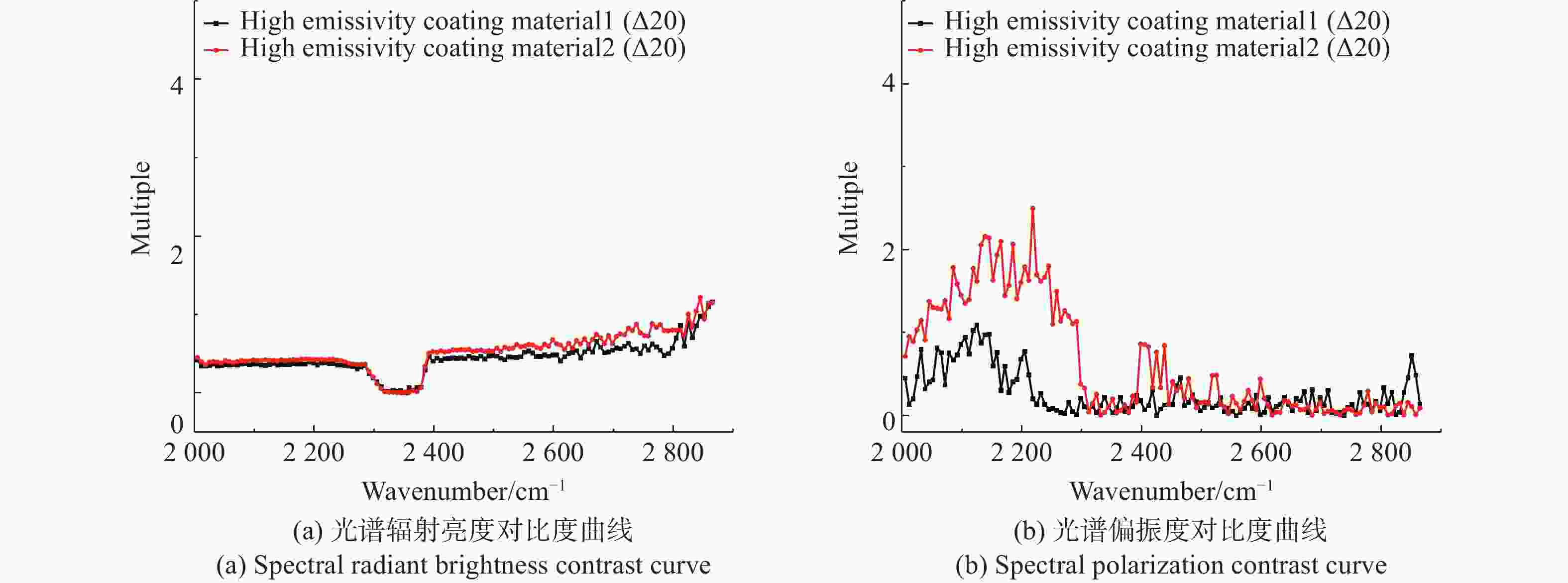
由上述可知，基底相同的材质表面涂敷不同的发射率涂层，不影响材质表面的红外光谱偏振特性。而基底不同，表面涂敷相同发射率的涂层，其表面红外辐射特征通常差异比较小。为了验证基底不同但涂敷相同发射率涂层材质的光谱偏振特性差异，课题组还开展了涂敷相同发射率(0.9)涂层的不同基底材质的红外高光谱偏振成像试验，试验中涂层材质均可以实现可控加热。将两种涂敷相同发射率涂层的不同基底材质加热到相同的辐射温度，通过红外高光谱偏振成像系统进行探测分析。图6为高发射率涂层材质1以及高发射率涂层材质2在辐射温度差异为20 ℃时的表面光谱辐射亮度对比度、表面光谱偏振度对比度曲线图，图6(a)、(b)中纵坐标分别为红外光谱辐射亮度对比度、红外光谱偏振度对比度。由图可知，在相同辐射温差条件下，基底材料不同、发射率相同的涂层材质表面光谱偏振度对比度与光谱辐射亮度对比度相比，材质表面光谱偏振度对比度有明显差异，且具有波段选择性。也就是说，即使不同材质涂覆相同涂层，由于其基底材料不同，偏振特性将比辐亮度值更具有明显的差异性。
图 6 不同基底的高发射率涂层材质光谱辐射亮度对比度及光谱偏振度对比度曲线图
Figure 6. Contrast curves of spectral radiation brightness and spectral polarization of high emissivity coatings with different substrates
-
由理论分析和试验验证可知：基于红外光谱偏振度对比度特征的材质探测对于涂层材质识别判定具有较明显的优势。文中首先基于目标材质表面的红外辐射偏振特性模型推导分析了表面发射率对目标材质表面红外偏振特性的影响，通过试验验证得出：改变发射率不影响目标材质表面红外线偏振度特征的初步结论；其次，结合理论推导分析开展了相同基底材质涂覆不同发射率涂层和不同基底材质涂覆相同发射率涂层材质的红外高光谱偏振成像试验研究，提出了基于红外光谱偏振度对比度的评价方法。基于红外光谱偏振度对比度的涂层材质识别研究结果表明：通过改变涂层材质表面发射率的方法可以改变材质表面的红外辐射特征，但其表面红外光谱偏振度并不会发生大的变化；基底材质是影响目标材质表面红外偏振特性的主要影响因素，且具有波段选择性。
后续课题组会继续开展典型基底材质的红外辐射偏振特性试验研究，并建立典型基底材质红外光谱偏振度对比度特征库。由于目前红外伪装材料常用的控温方法就是通过改变材质表面涂层的发射率来实现红外伪装[6-8]，故文中研究成果也可为红外伪装目标探测识别提供理论和实验基础支撑，有利于提高红外伪装材质探测识别的有效性，并可为进一步提高红外伪装材料有效性设计研制提供理论依据和技术支撑。
Research on coating materials detection and recognition based on infrared spectral polarization degree contrast
-
摘要:
为了降低材质红外识别的正确率，较常用的方法是通过在材质表面涂覆涂层，以改变材质的表面发射率。首先通过基于微面元理论的目标材质表面红外辐射偏振传输模型的Stokes表达式，推导分析了目标材质表面发射率对目标材质表面红外偏振特性的影响，结果表明：目标材质表面发射率的改变不影响其表面的红外线偏振度特征；其次，针对材质表面发射率与红外偏振特性的不相关性，文章提出基于光谱偏振度对比度检测涂层材质的方法，并通过相同基底不同表面发射率的涂层材质、不同基底相同发射率的涂层材质的红外高光谱偏振成像特性进行了验证分析，结果表明：改变涂覆材料表面发射率并不影响材质表面的红外光谱偏振度特征；基底材料不同，即使目标材质表面涂覆相同发射率涂层，其表面的光谱偏振度特性将比光谱辐射亮度具有更明显的差异性，研究成果可为红外伪装材质检测识别提供新的途径和方法。
Abstract:In order to reduce the accuracy of material infrared recognition, a common method was presented to change the emissivity of material surface by coating the material surface. Firstly, the influence of the surface emissivity of the target material on the infrared characteristics of the target material was deduced and analyzed through the Stokes expression of the infrared radiation polarization transmission model of the target material based on the micro-plane element theory. The theoretical analysis results show that the change of the surface emissivity of the target material does not affect the infrared polarization of the surface. Secondly, in view of the irrelevance between the material surface emissivity and infrared polarization characteristics, this method of coating material was proposed based on the spectral degree of polarization contrast. And the infrared hyperspectral polarization imaging characteristics of coating materials with different surface emissivities on the same substrate and coating materials with the same emissivity on different substrates were verified and analyzed. The results show that the change of the surface emissivity of the coated material does not affect the polarization degree of the infrared spectrum. And even if the target material is coated with the same emissivity coating, the characteristic of spectral polarization degree is more obviously different than that of spectral radiation brightness. The research results can provide a new method for infrared camouflage material detection and recognition.
-
图 2 低发射率涂层材质在40 ℃时中、长波红外光谱偏振度模拟结果与测量结果对比图
Figure 2. Contrast curves of infrared spectural polarization degree of low emissivity coating materials at the temperature of 40 ℃
图 4 不同涂层材质在相同辐射温度条件下的中波红外辐射强度图像和红外线偏振度图像
Figure 4. Mid-wave infrared radiation image and mid-wave infrared linear polarization degree image of different coating materials at the same temperature
图 5 相同基底的高、低发射率涂层材质光谱辐射亮度对比度及光谱偏振度对比度曲线图
Figure 5. Contrast curves of spectral radiation brightness and spectral polarization of high and low emissivity coatings with the same substrate
-
[1] 赵金榜. 国外隐身涂料及其发展[J]. 上海涂料, 2001(5): 19−23. doi: 10.3969/j.issn.1009-1696.2001.05.005 Zhao Jinbang. Stealthy coating and their development abroad [J]. Shanghai Coatings, 2001(5): 19−23. (in Chinese) doi: 10.3969/j.issn.1009-1696.2001.05.005 [2] 张辉, 张建春. 热红外隐身技术与人体伪装[J]. 上海纺织科技, 2003(2): 48−50. doi: 10.3969/j.issn.1001-2044.2003.02.021 Zhang Hui, Zhang Jianchun. Thermal infrared stealth technology and human body camouflage [J]. Shanghai Textile & Technology, 2003(2): 48−50. (in Chinese) doi: 10.3969/j.issn.1001-2044.2003.02.021 [3] Fulghum Dvaid A. New look at stealth [J]. Aviation Week and Space Technology(NewYork), 2003, 159(15): 24−29. [4] 陈伟力, 王淑华, 金伟其, 等. 基于偏振微面元理论的红外偏振特性研究[J]. 红外与毫米波学报, 2014, 33(5): 507−514. doi: 10.11972/j.issn.1001-9014.2014.05.009 Chen Weili, Wang Shuhua, Jin Weiqi, et al. Research of infrared polarization characteristics based on polarization Micro-surface theory [J]. J Infrared Millim Waves, 2014, 33(5): 507−514. (in Chinese) doi: 10.11972/j.issn.1001-9014.2014.05.009 [5] Howe James D, Miller Miranda A, Blumer Robert V, et al. Polarization sensing for target acquisition and mine detection[C]//SPIE, 2000, 4133: 202-213. (in Chinese) [6] 孙玮, 刘政凯, 单列. 利用偏振技术识别人造目标[J]. 光学技术, 2004, 30(3): 267−269. doi: 10.3321/j.issn:1002-1582.2004.03.005 Sun Wei, Liu Zhengkai, Shan Lie. Manmade objects recognition with polarization information [J]. Optical Technique, 2004, 30(3): 267−269. (in Chinese) doi: 10.3321/j.issn:1002-1582.2004.03.005 [7] 王宪栋, 赵尔波. 红外隐身涂料的研究现状与发展趋势[J]. 电子对抗, 2012(2): 246−49. Wang Xiandong, Zhao Erbo. Current research and development technology of infrared stealthy coatings [J]. Electronic Warfare, 2012(2): 246−49. (in Chinese) [8] 侯文学, 张晓光. 可见光、激光、毫米波与红外的复合隐身技术[J]. 航天电子对抗, 2003(3): 34−37. doi: 10.3969/j.issn.1673-2421.2003.03.010 Hou Wenxue, Zhang Xiaoguang. Composite stealth technology of visible light, laser, millimeter wave and infrared [J]. Space Electronic Warfare, 2003(3): 34−37. (in Chinese) doi: 10.3969/j.issn.1673-2421.2003.03.010 -
点击查看大图
计量
- 文章访问数: 1510
- HTML全文浏览量: 866
- 被引次数: 0
