-
鬼成像(Ghost Imaging)是一种新兴的成像技术，它利用信号光场和参考光场的相关性对目标进行成像。近年来，由于其独特的成像机制，鬼成像技术受到了研究人员的广泛关注。
1995年，史砚华小组首次利用纠缠光子对实现了鬼成像[1]。之后，研究人员又发现可以利用赝热光源[2-3]来实现鬼成像。随着空间光调制技术的发展，研究人员提出了计算式鬼成像技术(Computational Ghost Imaging，CGI，也称为单像素成像)[4-5]，将鬼成像中的双臂测量机制变为单臂测量，大大降低了成像系统的复杂度。此外，为了提高图像的重构质量与重构效率，人们也提出了压缩感知鬼成像[6]和差分鬼成像[7]等算法。
随着成像理论的逐渐完善，单像素成像技术也逐渐拓展到应用层面，如3D成像[8-9]、多光谱成像[10-11]、气体成像[12]等。2012年，韩申生等人将双臂鬼成像系统应用到激光雷达领域[13]，随后实现了对速度未知的移动目标进行探测[14]，以及在低于Nyquist采样极限的情况下实现3D遥感探测等研究[15]。此后，孙鸣捷等人利用单像素成像系统，实现了深度目标的探测[16]。在光谱探测领域，Liheng Bian实现了450 ~650 nm的单像素多光谱成像[10]，Vincent Studer实现了基于压缩感知的生物体的高光谱单像素成像[11]。Miles小组利用单像素成像系统，成功地实现了对甲烷气体的探测[12]。
2013年，Chen Wen等人提出将计算式鬼成像应用于目标认证领域[17]。随后研究人员对目标识别技术与鬼成像的结合进行了深入的研究。2017年，Wu Jingjing提出了一种基于相位匹配滤波的光学安全图像验证系统[18]。2018年，Chen Huichao等人提出了一种基于傅里叶频谱的非成像式目标识别的方案[19]。
2018年，东京大学的Sadao Ota等人提出了基于单像素成像系统进行血细胞计数的装置[20]，他们以血细胞的不同细胞结构的测量强度值作为血细胞的标记，以此训练识别模型，成功地实现了高速血细胞计数，相较于传统方法，该技术的计数速率显著提高。该项工作是单像素领域在目标识别方面的重要进步，因为它仅利用目标在不同模板上的投影值，实现对特定目标特征的标记，并以此训练和识别模型。
除此以外，Jiao Shuming等人提出了基于单像素成像系统的光学机器学习方法，实现了线性模式识别任务[21]。Zhang Zibang等人通过设计和训练卷积神经网络，使其学习目标特征，并将训练结果反馈到空间光调制器上，使其可以对目标进行有针对性的压缩测量，最终实现非成像式的高速目标识别[22]。
由此可见，在单像素成像系统中，利用机器学习进行目标识别具有重要的研究价值。但在实际成像过程中，噪声决定了系统的成像质量，进而影响了目标的识别。针对该问题，文中分别采用桶探测器获取的信号值和重构出二维图像作为训练样本进行深度学习，并以此识别噪声环境中的目标。
-
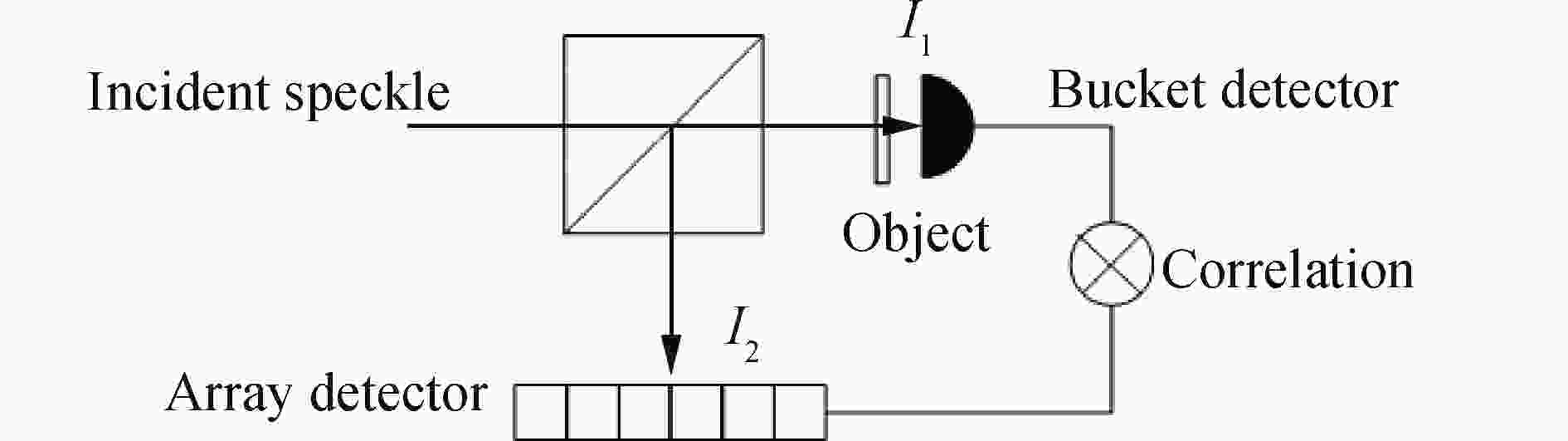
该系统的工作原理如图1所示。图1实线框中为单像素成像系统，其工作流程为：目标被光源照射后，经透镜成像于数字微镜器件（Digital Micromirror Device，DMD）表面。DMD通过加载一系列随机二值图案实现对目标空域图像的调制。经过调制后的信号经过收集透镜，被桶探测器接收。在测量过程中，规定第i帧加载图像为
$ {I_i}\left( x \right)$ ，其对应的桶探测器测量值为Bi，那么目标图像可以由关联算法重构。
图 1 实验流程图
Figure 1. Procedure of experiment
$$G\left( x \right) = \left\langle {{I_i}\left( x \right){B_i}} \right\rangle - \left\langle {{I_i}\left( x \right)} \right\rangle \left\langle {{B_i}} \right\rangle $$ (1) 式中：
$ \left\langle \ldots \right\rangle $ 表示对NS次测量进行系综平均。单像素成像可以理解为：通过对目标进行随机的空域测量，并利用相应的测量值对目标进行重构。由于每个目标的形态各不相同，因此在测量过程中，每一帧调制图案对应的桶探测器值已经携带了目标特征，当对目标进行多次测量后，这一系列桶探测器的测量值组成的向量可以看作目标的标记。
为了实现噪声环境下的目标识别，文中分别生成了两种样本进行深度学习：
（1）对一个目标在一个固定采样率下进行多次测量，得到一系列测量值，生成一组一维信号。重复以上测量过程，生成多组样本。虽然这些组对应的测量矩阵一致，但由于噪声的存在，导致各组的强度分布各不相同，所以可以作为这个目标的训练样本。由于未对目标进行重构，故称作非重构样本；
（2）基于桶探测器获取的一系列测量值，根据公式（1）重构出相应的目标图像，称作重构样本。文中以这两种样本对模型进行训练和测试。
-
对于非重构样本，假设第i次桶探测器测量值为Bi，其中噪声大小为ni。其信噪比可以表示为：
$$SN{R_{1D}} = \frac{{\left\langle {{B_i}} \right\rangle }}{{\sigma _n^2}}$$ (2) 式中：σn2是噪声方差。可以看出，当直接利用桶探测器测量值作为训练样本时，样本的信噪比会随着测量次数的增加而变得更稳定，统计特征（
$ \left\langle {{B_i}} \right\rangle $ 和σn2）更加明显。对于重构样本，文中首先回顾基于赝热光源的鬼成像信噪比理论[3]，系统简图如图2所示。
图 2 基于赝热光源的经典鬼成像系统简图
Figure 2. Classical ghost imaging system based on thermal source
用
$ {I_1}\left( {{x_1}} \right)$ 表示到达目标平面光场的强度分布，$ {I_2}\left( {{x_2}} \right)$ 表示到达面阵探测器光场的强度分布，其中x1，x2表示其两个光场的横向位置坐标。在此，假设从光源传播到目标和到面阵探测器的距离相等。文中采用Ferri等人的分析方法[7]，设目标的透过率函数为$T(x)$ ，那么桶探测器的测量值可以表示为：$$ {{S}_{1}}=\int_{{\rm{beam}}}\,{{I}_{1}}\left( {{x}_{1}} \right)T\left( {{x}_{1}} \right)d{{x}_{1}} $$ (3) 这里桶探测器值S1与公式(2)中Bi具有一致的物理意义，但为了推导的一致性，文中在这里延用参考文献[7]中的表示方法。基于赝热光源的鬼成像的成像式可以写成：
$$\left\langle {G\left( {{x_2}} \right)} \right\rangle = \left\langle {\delta {S_1}\delta I\left( {{x_2}} \right)} \right\rangle $$ (4) 式中：
$ \delta {S_1} = {S_1} - \left\langle {{S_1}} \right\rangle ,\delta {I_2}\left( {{x_2}} \right) = {I_2}\left( {{x_2}} \right) - \left\langle {{I_2}\left( {{x_2}} \right)} \right\rangle $ ，$ \left\langle \ldots \right\rangle $ 表示对多个散斑的系综平均。当散斑的横向相干距离足够小时，成像结果可以写成：$$\left\langle {G\left( {{x_2}} \right)} \right\rangle = {A_{coh}}\left\langle {{I_1}\left( {{x_2}} \right)} \right\rangle \left\langle {{I_2}\left( {{x_2}} \right)} \right\rangle T\left( {{x_2}} \right)$$ (5) 为了简化分析，假设分束器的分束强度比例为1:1，目标所处的区域光强均匀，则
$ {I_1}\left( {{x_1}} \right)$ ，$ {I_2}\left( {{x_2}} \right)$ 可简写为I1和I2。那么基于经典光源鬼成像系统中的信号，噪声和信噪比可以表示为[7]：$$\begin{split} {\rm{Signal}} = \; & {\left( {\Delta \left\langle {G\left( {{x_2}} \right)} \right\rangle } \right)^2}=\\ & A_{{\rm{coh}}}^2{\left\langle {{I_1}} \right\rangle ^2}{\left\langle {{I_2}} \right\rangle ^2}{\left( {\Delta T} \right)^2} \end{split}$$ (6) $$ \begin{split} {\rm{Noise}} = \;&\left\langle {\Delta {G^2}} \right\rangle \approx \left\langle {{G^2}} \right\rangle =\\ & {A_{{\rm{coh}}}}{A_{{\rm{beam}}}}{{\left\langle I_1 \right\rangle }}^2{{\left\langle {{I_2}} \right\rangle }^2}\overline {{T^2}} \end{split} $$ (7) $$ SNR = \frac{{{\rm{Signal}}}}{{{\rm{Noise}}}} = \frac{M}{{{N_{sp}}}}\frac{{{{\left( {\Delta T} \right)}^2}}}{{\overline {{T^2}} }} $$ (8) 式中：Acoh表示散斑的相干面积；Abeam表示散斑的总面积。
$ \Delta \left\langle {G\left( {{x_2}} \right)} \right\rangle $ 的最小波动被定义为信号；∆T表示目标透过率(针对透射式目标)的最小变化幅度；$ \overline {{T^2}} $ 表示目标的平均透过率。假设桶探测器噪声大小为nsig
，面阵探测器噪声为 $ {n_{{\rm{ref}}}}\left( {{x_2}} \right)$ 。那么含有噪声的桶探测器测量值S1n和含有噪声的面阵探测器的测量值$ {I_{2n}}\left( {{x_2}} \right)$ 分别为：$${S_{1n}} = {n_{{\rm{sig}}}} + {S_1}$$ (9) $${I_{2n}}\left( {{x_2}} \right) = {n_{{\rm{ref}}}}\left( {{x_2}} \right) + {I_2}\left( {{x_2}} \right)$$ (10) 在计算式鬼成像系统中，
$ {n_{{\rm{ref}}}}\left( {{x_2}} \right) = 0$ 。首先推导信号项，将公式（9）和公式（10）代入公式（4）中得：$${\left\langle {G\left( {{x_2}} \right)} \right\rangle _n} = \left\langle {\delta \left( {{n_{{\rm{sig}}}} + {S_1}} \right)\delta \left( {{I_2}\left( {{x_2}} \right)} \right)} \right\rangle $$ (11) 由于噪声项nsig与探测到的信号值互相独立，且均值为0，将公式（11）展开后化简得到：
$${\left\langle {G\left( {{x_2}} \right)} \right\rangle _n} = \left\langle {\delta {S_1}\delta {I_2}\left( {{x_2}} \right)} \right\rangle $$ (12) 下面分析器件噪声对信噪比中噪声项的作用。将公式(9)(10)代入公式(7)，可以得到：
$${\left\langle {{G^2}} \right\rangle _n} = \left\langle {{{\left( {\delta {S_1} + \delta {n_{{\rm{sig}}}}} \right)}^2}{{\left( {\delta {I_2}} \right)}^2}} \right\rangle $$ (13) 将公式（13）展开后化简可以得到：
$${\left\langle {{G^2}} \right\rangle _n} = \left\langle {{{\left( {{\rm{\delta }}{S_1}} \right)}^2}{{\left( {{\rm{\delta }}{I_2}} \right)}^2}} \right\rangle + \sigma _{{\rm{sig}}}^2\left\langle {{{\left( {{\rm{\delta }}{I_2}} \right)}^2}} \right\rangle $$ (14) 基于公式（12）和公式（14）得出的结论，含有器件噪声的计算鬼成像系统信噪比表达式可以写为：
$$SN{R_n} = \frac{{{{\left( {\Delta G} \right)}^2}}}{{\left\langle {{G^2}} \right\rangle + \sigma _{{\rm{sig}}}^2\left\langle {{{\left( {\delta {I_2}} \right)}^2}} \right\rangle }}$$ (15) 经过化简得：
$$SN{R_n} = \frac{{M{{\left( {\Delta T} \right)}^2}}}{{{N_{sp}}\overline {{T^2}} + \frac{a}{{{{\left\langle {{I_1}} \right\rangle }^2}}}\sigma _{{\rm{sig}}}^2}}$$ (16) 式中：
$ a = \left\langle {{{\left( {\delta {I_2}} \right)}^2}} \right\rangle /A_{{\rm{coh}}}^2{\left\langle {{I_2}} \right\rangle ^2}$ ，当散斑的相干长度不变，a对于计算式鬼成像系统是一个常数。从公式(16)可以看出，随着迭代的进行，σsig2会趋于稳定，重构图像信噪比SNRn也会随着采样数M的增大而增大，图像质量逐步提升。 -
当单像素探测器的测量值包含噪声时，对应样本的局部信息会被噪声破坏，目标特征变得难以提取，从而降低目标识别率。
在基于神经网络的目标识别方法中，对于含噪声图像，Nascimento等人基于卷积神经网络，提出了一种全局环境结构和局部目标特征的识别方法，提高了其在噪声环境中算法鲁棒性[23]。Zhang Wei等人通过改进CNN的结构，提出了一种带训练干扰的卷积神经网络(TICNN)，可以直接在原始的嘈杂信号上工作[24]。此外，为了强化神经网络对含噪声图像的特征学习能力，研究人员在传统卷积神经网络的基础上，增加卷积层的数量（如VGG模型[25]），以减小噪声对目标特征提取的影响，提高识别精度[26-27]。
由于网络层数的增加会带来梯度爆炸的问题。为此，研究人员在VGG模型的基础上提出了ResNet[28]。该方法在卷积神经网络的基础上，引入了快速结构，如图3(a)所示。该结构中，Weight Layer表示卷积层，ReLu为激活函数，两层卷积网络的输出为
$ F(x)$ 。输入信号x除了产生了$ F(x)$ ，还直接累加到$ F(x)$ 上，使输出变成$ F(x)+x$ 。这种快速结构保证了在反向传播时信号可以无衰减地传递，从而避免了在层数较多时出现的梯度爆炸现象。研究表明，ResNet在网络层数更深的情况下保持较高的识别精度[29-31]。
图 3 ResNet和ResNet_V2的构成。 (a) ResNet的构成；(b) ResNet_V2的构成
Figure 3. Composition of ResNet and ResNet _V2. (a) Composition of ResNet; (b) composition of ResNet_V2
文中采用ResNet_v2_50模型[32]进行训练，其结构在图3（a）的基础上进行了调整，如图3（b）所示。其中，BN表示Batch Normalization，“50”表示卷积层的数量。
-
文中采用华为Modelarts平台作为训练和识别平台，该平台是以图像作为目标，因此文中将一维数据进行矩阵重排，保存为二维图像作为训练样本。由于成像系统噪声随机起伏，导致桶探测器的测量值波动较大，直接保存为灰度图像容易造成数据溢出，导致非线性失真。
针对这个问题，文中采用伪彩色映射的方法，将具有较大波动范围的桶探测器数据映射到具有固定值域的伪彩色区域，即利用彩色信息表示波动较大的灰度图像，防止溢出。
假设单个非重构样本的采样数为NS，其桶探测器信号表示为
$ {\hat B_i}\left( {i = 1 \ldots {N_S}} \right)$ 。$ {\hat B_i}$ 的物理意义是由Bi组成的一维向量。其次，在单一场景下包含不同噪声的非重构样本个数为Q，记为
$ {\left\{ {{{\hat B}_i}} \right\}_q}\left( {q = 1\cdots Q} \right)$ 。设伪彩色映射的值域上限为Vmax，下限为Vmin，那么Vmax，Vmin由公式(17)决定。 $$\left\{ {\begin{aligned} & {{V_{{\rm{max}}}} = {{{\rm{max}}}}\left( {{{\left\{ {{{\hat B}_i}} \right\}}_q}} \right) + \Delta }\\ & {{V_{{\rm{min}}}} = {{{\rm{min}}}}\left( {{{\left\{ {{{\hat B}_i}} \right\}}_q}} \right) - \Delta } \end{aligned}} \right.$$ (17) 式中：
$ {\rm{max}}\left( {{{\left\{ {{{\hat B}_i}} \right\}}_q}} \right)$ 和$ {\rm{min}}\left( {{{\left\{ {{{\hat B}_i}} \right\}}_q}} \right)$ 分别表示集合$ {\left\{ {{{\hat B}_i}} \right\}_q}$ 中的最大值和最小值，∆为冗余量，其作用是为了减少在测试样本中可能出现的超过值域的情况。确定了Vmax和Vmin后，对训练样本中每个$ {{{\hat B}_i}}$ 进行重排。为了便于数据操作，重排后图像的行/列包含相等数目的像素块，如图4所示。
图 4 非重构信号重排方法及伪彩色映射方式
Figure 4. Rearrangement of non-imaged samples and pseudo-color mapping method
为了比较基于非重构样本与基于重构样本的识别结果，文中利用公式(1)重构了每一个
$ {{{\hat B}_i}}$ 对应的二维目标图像，所有非重构样本对应的重构图像标记为$ \left\{ {{G_q}} \right\}\left( {q = 1..Q} \right)$ ，并根据重构图像的灰度值不同，采用了与公式(17)相似的映射方法，对{Gq}进行伪彩色映射，如公式(18)所示。$$\left\{ {\begin{aligned} & {{V_{{\rm{max}}}} = {{{\rm{max}}}}\left( {\left\{ {{G_q}} \right\}} \right) + \Delta }\\ & {{V_{{\rm{min}}}} = {{{\rm{min}}}}\left( {\left\{ {{G_q}} \right\}} \right) - \Delta } \end{aligned}} \right.$$ (18) 在两种样本中，每个像素块的大小一致。
-
下面对文中提出的方法进行仿真验证。成像目标是0~9这10个数字，目标的空间分辨率为32×32。对于一种分辨率的目标，分别进行了不同采样率的采样，并添加了不同的噪声。添加噪声的过程是：
$${\hat B_{i\_n}} = {\hat B_i} + \hat n$$ (19) 式中：
$ {\hat B_i}$ 和$ {\hat B_{i\_n}}$ 分别是不含噪声和含有噪声的桶探测器信号；$ \hat n$ 是一维噪声，与$ {\hat B_i}$ 长度相等，其均值$ {\mu _n} = 0$ ，方差$ \sigma _n^2 = \dfrac{1}{{12}}\varepsilon {\rm{max}}\left( {{{\hat B}_i}} \right)\left( {i = 2 \ldots {N_S}} \right)$ ，其中ε为添加噪声的比例。在文中，采样率β分别为4.7%，9.7%，21.9%和39%，噪声比例ε分别为$ 20\% ，30\% $ 和40%。在每一种情况下（一种情况对应一个确定的β和一个确定的ε），用于训练的样本数为1 500个，用于检测的样本数为300个。文中分别研究了在不同采样率和不同噪声强度下的目标识别率（如表1和表2所示）、预处理时间（如图5(a)所示）以及推理时间（如图5(b)所示）。表 1 基于非重构样本的识别结果
Table 1. Recognition results using non-imaged samples
ε=20% ε=30% ε=40% β=4.7% 99% 97% 87% β=9.7% 98% 100% 90% β=21.9% 100% 91% 72% β=39% 97% 88% 58% 表 2 基于重构样本的识别结果
Table 2. Recognition results using imaged samples
ε=20% ε=30% ε=40% β=4.7% 99% 98% 89% β=9.7% 100% 94% 91% β=21.9% 100% 100% 97% β=39% 100% 100% 98% 
图 5 基于非重构样本与重构样本的识别方法所需预处理（a）与推理时间（b）
Figure 5. Preprocessing (a) and inferring (b) time for the recognition methods using non-imaged and imaged sample respectively
从表1，2可以看出，这两种方法在采样率固定时（β固定），其识别率总体上都会受到噪声的影响，噪声幅度越高，识别率越低。
当噪声程度较低时（ε≤30%）时，两种方法在不同采样率下的识别率都较高，但基于非重构样本的识别方法具有处理时间上的优势。
由图5可以看到，即使采样率不同，两种方法的单次推理时间基本一致，均在0.26 ms左右。但是基于重构样本的模型单次识别的预处理时间稳定在7.8 ms左右，这是由于这种方法在每次识别中均需要重构分辨率一致的目标图片。
而对于基于非重构样本训练的模型，单次识别时间随着采样率的上升而上升，该仿真给定条件下的预处理时间由1.79 ms稳定增加到4.27 ms。这说明采样数越少，基于非重构样本的识别方法的时间优势越明显。
当噪声程度较高时（ε=40%），基于重构样本的识别方法识别率随着采样数的增加而提高。根据公式（16）可知，当采样次数上升后，重构图像的信噪比提高，图像质量变好，因此识别率升高。但仍存在着预处理时间较长的问题。
而对基于非重构样本的识别方法而言，虽然噪声较高时，采样率上升会引起识别率显著下降（采样率达到39%时，识别率下降到58%）。这种现象的可能原因是：在对于非重构样本而言，采样率提高并未增加样本自身的信噪比（见公式(2)）。当采样率更高的含噪声样本输入ResNet全连接层时，噪声相互混叠，从而影响了识别准确率。但最重要的是，在采样率较低的情况下(β≤10%)，该方法的识别率仍保持较高水平（识别率为90%左右）。由于其在预处理方面的优势，该方法在含噪声的快速成像领域中具有一定的应用潜力。
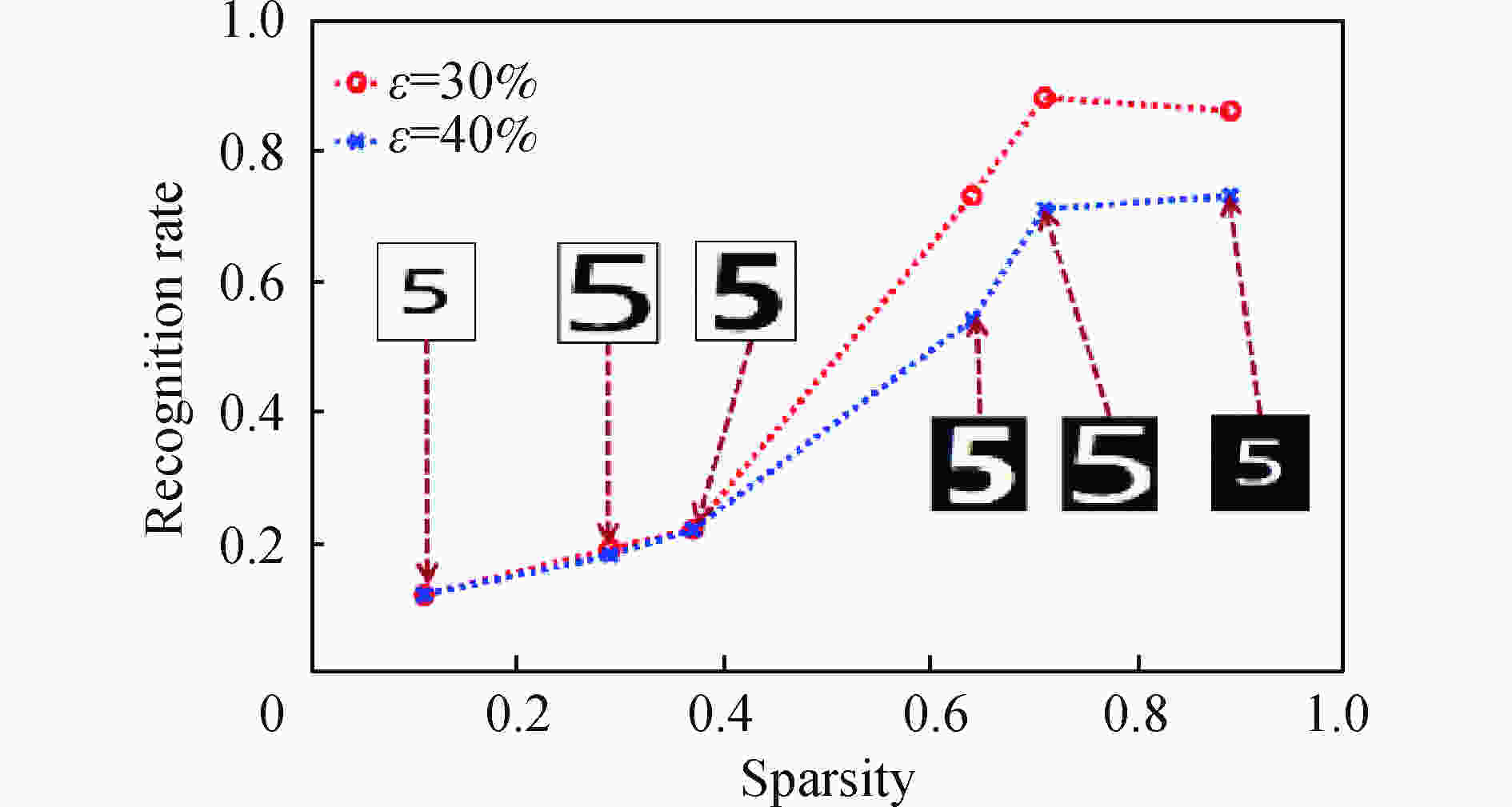
文中还研究了当采样率和噪声程度一定时，目标图像的稀疏度对基于非重构样本的识别方法的影响。这里稀疏度的定义如公式(20)所示，其中Nzero和Nwhole分别表示图像中0的数量和总像素的数量。
$$sparsity = \frac{{{N_{{\rm{zero}}}}}}{{{N_{{\rm{whole}}}}}}$$ (20) 文中共生成了6组不同稀疏度的数字目标。各组图像大小一致，平均稀疏度分别为：11%、28.6%、36.5%、63.5，71%和89%。对于单个样本中，共采样225次，采样率为9.7%。每组图像包括1500个训练样本，300个测试样本，分别在两个噪声条件下，进行目标识别，识别结果如图6所示。
图 6 不同稀疏度目标的识别率
Figure 6. Recognition accuracy for the targets with different sparsity ratios
可以看到，在不同的噪声比例时，目标识别率都随着目标图像的稀疏度的增加而上升。当目标图像的稀疏度为11%，28.6%以及36.5%时，该方法的识别率在不同噪声情况下都低于50%。而对于稀疏度为63.5，71%，89%的目标，该方法识别率有明显上升。例如，在噪声程度为ε=30%，稀疏度为71%和89%时，识别率可以稳定在80%左右。即使噪声增加到ε=40%，这两种目标的识别率也稳定在70%左右。
由此可以看出，在噪声比例和采样数一定时，基于非重构样本的识别方法对稀疏度较高的目标图像有更好的识别效果。需要说明的是：表1、表2对应成像目标的稀疏度约为95%，其在β=9.7%, ε=30%，40%的识别率约为90%，高于图6所示同等条件的识别率，进一步印证了这一结论。
-
文中针对噪声环境中单像素成像系统的目标识别方法展开研究，分别采用桶探测器获取的信号值和重构出的二维图像作为训练样本进行深度学习，并以此识别噪声环境中的目标。
研究发现，基于非重构样本的识别方法在采样率较低且噪声较强的情况下，仍具有良好的识别率，且预处理时间较短。而对于基于重构目标的识别方法，虽然其识别率较高，但是其预处理时间较长。因此基于非重构样本的识别方法更适合需要快速成像的应用场景。此外，文中还研究了目标稀疏度对基于非重构样本的识别方法的影响，发现当噪声程度和采样率一定时，目标越稀疏，识别率越高。文中为处于噪声环境中（尤其是需要高速成像的应用环境）的目标识别应用提供了研究依据。
Target recognition method based on single-pixel imaging system and deep learning in the noisy environment
-
摘要:
单像素成像系统由于其独特的成像方式受到广泛关注，但其在噪声环境中的目标识别方法并未得到深入研究。针对该问题，文中分别采用桶探测器获取的信号值和重构出的二维图像作为训练样本进行深度学习，并以此识别噪声环境中的目标。通过对比两者识别结果，发现在采样率较低时，前者即使在较强噪声环境中也可以获得较高的识别率；而后者的识别率虽然一直比较稳定，但其预处理时间较高，因此前者更适用于快速成像中的目标识别。此外，对于仅利用桶探测器信号进行训练的方法，文中还研究了目标稀疏度对其识别精度的影响，发现当外界噪声和采样率一定时，稀疏度越高的目标，其识别精度也越高。文中为噪声环境中单像素成像的目标识别方法提供了选择依据。
Abstract:Single-pixel imaging system attracts a lot of attentions because of its special imaging method, but its target recognition method in noisy environment has not been studied deeply. Aiming at this problem, the signal sequences obtained by the bucket detector and the corresponding formed two-dimensional images were used as the training samples for deep learning to identify targets in noisy environments. By comparing the recognition results of these two methods, it was found that when the sampling rate was low, the former one could obtain a higher recognition rate even in a strong noise environment; while for the latter one, although the recognition rate was relatively stable, its preprocessing time was high, so the former one was more suitable for target recognition in high-speed imaging. In addition, for the method using only the bucket detector signal as the training samples, the effect of target sparsity on its recognition accuracy was also analyzed. It was found that when the external noise and sampling rate were fixed, the higher the sparsity of the target, the higher the recognition accuracy was. This paper can be used as the reference for the selection of single pixel system recognition methods in noisy environments.
-
Key words:
- ghost imaging /
- target recognition /
- deep learning
-
图 3 ResNet和ResNet_V2的构成。 (a) ResNet的构成；(b) ResNet_V2的构成
Figure 3. Composition of ResNet and ResNet _V2. (a) Composition of ResNet; (b) composition of ResNet_V2
图 4 非重构信号重排方法及伪彩色映射方式
Figure 4. Rearrangement of non-imaged samples and pseudo-color mapping method
图 5 基于非重构样本与重构样本的识别方法所需预处理（a）与推理时间（b）
Figure 5. Preprocessing (a) and inferring (b) time for the recognition methods using non-imaged and imaged sample respectively
图 6 不同稀疏度目标的识别率
Figure 6. Recognition accuracy for the targets with different sparsity ratios
表 1 基于非重构样本的识别结果
Table 1. Recognition results using non-imaged samples
ε=20% ε=30% ε=40% β=4.7% 99% 97% 87% β=9.7% 98% 100% 90% β=21.9% 100% 91% 72% β=39% 97% 88% 58% 
下载: 导出CSV
表 2 基于重构样本的识别结果
Table 2. Recognition results using imaged samples
ε=20% ε=30% ε=40% β=4.7% 99% 98% 89% β=9.7% 100% 94% 91% β=21.9% 100% 100% 97% β=39% 100% 100% 98%
下载: 导出CSV
-
[1] Pittman T B, Shih Y H, Strekalov D V, et al. Optical imaging by means of two-photon quantum entanglement [J]. Physical Review A, 1995, 52(5): R3429. doi: 10.1103/PhysRevA.52.R3429 [2] Bennink R S, Bentley S J, Boyd R W. “Two-photon” coincidence imaging with a classical source [J]. Physical Review Letters, 2002, 89(11): 113601. doi: 10.1103/PhysRevLett.89.113601 [3] Ferri F, Magatti D, Sala V G, et al. Longitudinal coherence in thermal ghost imaging [J]. Applied Physics Letters, 2008, 92(26): 261109. doi: 10.1063/1.2945642 [4] Shapiro J H. Computational ghost imaging [J]. Physical Review A, 2008, 78(6): 061802. doi: 10.1103/PhysRevA.78.061802 [5] Bromberg Y, Katz O, Silberberg Y. Ghost imaging with a single detector [J]. Physical Review A, 2009, 79(5): 053840. doi: 10.1103/PhysRevA.79.053840 [6] Katz O, Bromberg Y, Silberberg Y. Compressive ghost imaging [J]. Applied Physics Letters, 2009, 95(13): 131110. doi: 10.1063/1.3238296 [7] Ferri F, Magatti D, Lugiato L A, et al. Differential ghost imaging [J]. Physical Review Letters, 2010, 104(25): 253603. doi: 10.1103/PhysRevLett.104.253603 [8] Sun M J, Zhang J M. Single-pixel imaging and its application in three-dimensional reconstruction: a brief review [J]. Sensors, 2019, 19(3): 732. doi: 10.3390/s19030732 [9] Sun B, Edgar M P, Bowman R, et al. 3D computational imaging with single-pixel detectors [J]. Science, 2013, 340(6134): 844−847. doi: 10.1126/science.1234454 [10] Bian L, Suo J, Situ G, et al. Multispectral imaging using a single bucket detector [J]. Scientific Reports, 2016, 6: 24752. doi: 10.1038/srep24752 [11] Studer V, Bobin J, Chahid M, et al. Compressive fluorescence microscopy for biological and hyperspectral imaging [J]. Proceedings of the National Academy of Sciences, 2012, 109(26): E1679−E1687. doi: 10.1073/pnas.1119511109 [12] Gibson G M, Sun B, Edgar M P, et al. Real-time imaging of methane gas leaks using a single-pixel camera [J]. Optics Express, 2017, 25(4): 2998−3005. doi: 10.1364/OE.25.002998 [13] Zhao C, Gong W, Chen M, et al. Ghost imaging lidar via sparsity constraints [J]. Applied Physics Letters, 2012, 101(14): 141123. doi: 10.1063/1.4757874 [14] Li E, Bo Z, Chen M, et al. Ghost imaging of a moving target with an unknown constant speed [J]. Applied Physics Letters, 2014, 104(25): 251120. doi: 10.1063/1.4885764 [15] Gong W, Zhao C, Yu H, et al. Three-dimensional ghost imaging lidar via sparsity constraint [J]. Scientific Reports, 2016, 6: 26133. doi: 10.1038/srep26133 [16] Sun M J, Edgar M P, Gibson G M, et al. Single-pixel three-dimensional imaging with time-based depth resolution [J]. Nature Communications, 2016, 7(1): 1−6. [17] Chen W, Chen X. Object authentication in computational ghost imaging with the realizations less than 5% of Nyquist limit [J]. Optics Letters, 2013, 38(4): 546−548. doi: 10.1364/OL.38.000546 [18] Wu J, Haobogedewude B, Liu Z, et al. Optical secure image verification system based on ghost imaging [J]. Optics Communications, 2017, 399: 98−103. doi: 10.1016/j.optcom.2017.04.042 [19] Chen H, Shi J, Liu X, et al. Single-pixel non-imaging object recognition by means of Fourier spectrum acquisition [J]. Optics Communications, 2018, 413: 269−275. doi: 10.1016/j.optcom.2017.12.047 [20] Ota S, Horisaki R, Kawamura Y, et al. Ghost cytometry [J]. Science, 2018, 360(6394): 1246−1251. doi: 10.1126/science.aan0096 [21] Jiao S, Feng J, Gao Y, et al. Optical machine learning with incoherent light and a single-pixel detector [J]. Optics Letters, 2019, 44(21): 5186−5189. doi: 10.1364/OL.44.005186 [22] Zhang Z, Li X, Yao M, et al. Image-free real-time classification of fast moving objects using learned spatial light modulation and a single-pixel detector[J]. arXiv preprint arXiv: 1912.01974, 2019. [23] Nascimento G, Laranjeira C, Braz V, et al. A robust indoor scene recognition method based on sparse representation[C]//Iberoamerican Congress on Pattern Recognition. Springer, Cham, 2017: 408-415. [24] Zhang W, Li C, Peng G, et al. A deep convolutional neural network with new training methods for bearing fault diagnosis under noisy environment and different working load [J]. Mechanical Systems and Signal Processing, 2018, 100: 439−453. doi: 10.1016/j.ymssp.2017.06.022 [25] Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition[J]. arXiv preprint arXiv: 1409.1556, 2014. [26] Du J. Research of anti-noise and energy-efficient deep neural networks for spontaneous facial expression recognition[D]. Guangzhou: Guangdong University of Technology, 2019. (in Chinese) [27] Zhang X, Liu W. Research on SAR target recognition based on convolutional neural networks [J]. Electronic Measurement Technology, 2018, 41(14): 92−96. (in Chinese) [28] He K, Zhang X, Ren S, et al. Deep residual learning for image recognition[C] //Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2016: 770-778. [29] Jiang S. Classification and description of fundus images based on ResNet[D]. Yantai: Shandong Technology and Business University, 2019. (in Chinese) [30] Tang K, He Q, Zhao Q, Wang X. Image recognition based on improved deep neural network [J]. Journal of Nanjing Normal University (Natural Science Edition), 2019, 42(3): 115−121. (in Chinese) [31] Wu K, Bai M. Study on recognition algorithm for plaque in coronary CTA on the basis of deep residual network [J]. China Medical Equipment, 2019, 16(11): 1−5. (in Chinese) [32] He K, Zhang X, Ren S, et al. Identity mappings in deep residual networks[C]//European Conference on Computer Vision. Springer, Cham, 2016: 630-645. -
点击查看大图
计量
- 文章访问数: 920
- HTML全文浏览量: 139
- 被引次数: 0
