-
数字条纹投影三维测量技术具有非接触、成本低和精度高等优点，在工业检测、机器视觉、逆向工程等领域得到大量应用[1]。其过程主要分为相位计算、相位展开、相位深度映射等步骤[2]。在相位计算的经典方法中，傅里叶变换法[3]测量速度快，但针对复杂面形物体，难以保持测量细节。相移法[4]具有高分辨率、高精度等优点，但需要至少三幅条纹图，在快速测量时会引入动态误差。相位计算得到的相位结果被包裹在
$( - \pi ,\pi ]$ 范围内，因此需要通过相位展开获得绝对相位[5]。相位展开通常分为空间相位展开与时间相位展开两类[6]。前者在复杂物体上的相位展开容易出现相位展开误差传递；而后者通过额外投影多帧光栅图像，能在时域内逐点进行正确相位展开。常用的时域方法有格雷码法、指数增长法、多频法等[7-8]。减少投影光栅图像帧数，同时满足实际测量精度需求，在快速测量领域具有重要意义，尤其在动态测量领域尤为重要。近年来，伴随着计算机性能的不断提高，深度学习取得了迅速发展，被广泛应用于计算机视觉、自然语言处理等领域，取得了令人瞩目的成果。与此同时，研究者们也开始将其应用到三维测量中。基于传统数字条纹投影三维测量技术中条纹投影、相位计算、相位展开、相位深度映射的流程，研究者们尝试使用深度神经网络替换其中部分或者整个环节，来提高测量效率或解决传统方法中的固有问题，如投影条纹信噪比、对比度、数量等。于浩天等人提出了FPTNet，使用一或两张条纹图生成多个不同频率的相移条纹图，进行相位计算及相位展开，可获得较为精确的三维形貌[9]。冯世杰等人基于卷积神经网络，使用三张条纹投影图作为神经网络的输入可获得物体的绝对相位，其精度与相移法相似[10]。尹维等人使用深度神经网络获取条纹级次，提高了双频相位展开算法的能力[11]。从应用角度出发，研究者们更希望使用深度学习直接从单帧条纹图获得物体三维形貌。H. Nguyen等人采用单阶段的网络，将传统方法中多个复杂的计算过程，替换为直接由单幅条纹图到深度之间的变换[12]。
综上，除相位深度映射步骤外，使用深度神经网络替换传统方法的其余环节已被证明具有可行性，因此，使用深度学习进行绝对相位到深度的映射是否可行，是文中研究的一个重要问题。另一方面，直接从单帧条纹图获得物体的三维形貌的单阶段网络测量方法舍弃了传统的物理过程，简化了计算流程，可以满足一定环境下的三维测量的需求，但是，这种单纯地利用数据驱动的方式是否合理，以及基于传统的物理测量过程设计网络模型是否更有意义，是值得我们探究的一个问题。
文中提出了一种PDNet (Phase to Depth Network)深度神经网络模型用于进行绝对相位到深度的映射，测量精度RMSE(均方根误差)达到了0.363 mm，能较准确地测量出物体的深度信息，证明了使用深度学习实现三维测量中绝对相位映射深度步骤的可行性，为后续使用深度神经网络进行标定参数等系数的优化，和将深度神经网络全面应用于数字条纹投影三维测量提供了参考。针对直接由单帧条纹图到深度值的端到端测量需求，文中基于已有的工作，将FPTNet与PDNet联合，提出了多阶段深度学习单帧条纹投影三维测量方法，该方法首先训练FPTNet实现单幅条纹图到不同频率下多组条纹图的转换，从而获得绝对相位，再对PDNet进行训练，实现绝对相位到深度值的映射。实验结果表明，相比于单阶段端到端深度学习单帧条纹投影三维测量方法，多阶段端到端深度学习单帧条纹投影三维测量方法在复杂场景上的测量误差降低了约4倍，精度提升显著。因此，单纯的采用数据驱动的方式增加了网络学习的难度，降低了测量精度，存在一定缺陷。而在分阶段进行网络的训练时，传统的物理测量过程会给予网络更多且更合理的约束，从而帮助网络获得较好的测量结果。
-
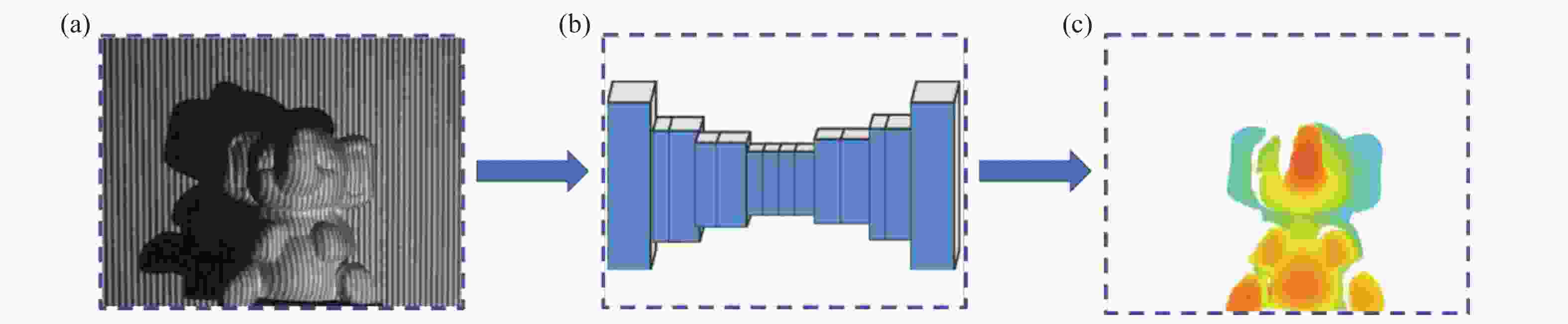
传统数字条纹投影三维测量技术主要包括条纹投影、相位计算、相位展开、相位深度映射等步骤。其测量过程如图1所示。文中首先关注绝对相位到深度的映射这一测量流程。
图 1 传统数字条纹投影方法进行三维测量。(a) 条纹投影图；(b) 包裹相位；(c) 绝对相位；(d) 物体深度图
Figure 1. 3D measurement of traditional digital fringe projection. (a) Fringe projection; (b) wrapped phase; (c) absolute phase; (d) depth
在传统数字条纹投影方法中，物体绝对相位
$\varphi $ 映射到物体深度使用系统标定参数经过一系列计算实现[13]，具体流程如下：设物体三维坐标为
$({x^w},{y^w},{z^w})$ ，则绝对相位$\varphi $ 与三维坐标的映射关系可用公式(1)与公式(2)表示:$${A_{\rm{c}}}{\{ {u^{\rm{c}}},{v^{\rm{c}}},1\} ^{\rm{T}}} = {P^{_{\rm{c}}}}{\{ {x^w},{y^w},{z^w},1\} ^{\rm{T}}}$$ (1) $${A_{\rm{p}}}{\{ {u^{\rm{p}}},{v^{\rm{p}}},1\} ^{\rm{T}}} = {P^{\rm{p}}}{\{ {x^w},{y^w},{z^w},1\} ^{\rm{T}}}$$ (2) 式中：
${A_{\rm{c}}}$ 、${A_{\rm{p}}}$ 为尺度因子常量；${P^{\rm{c}}}$ 、${P^{\rm{p}}}$ 分别为标定得到的相机、投影仪参数；$({u^{\rm{c}}},{v^{\rm{c}}})$ 为相机像素坐标；$({u^{\rm{p}}},{v^{\rm{p}}})$ 为投影仪像素坐标，由于通常只投影一个方向的条纹图像，因此只需计算${u^{\rm{p}}}$ ，通过公式(3)可以获得，其中$F$ 为投影条纹频率，$W$ 为投影仪横向分辨率。$${u_{\rm{p}}} = \frac{\varphi }{{F \times 2\pi }} \times W$$ (3) 根据公式(1)~(3)，可以建立公式(4)~(6)三个等式：
$${f_1}({x^w},{y^w},{z^w},{u^{\rm{c}}}) = 0$$ (4) $${f_2}({x^w},{y^w},{z^w},{v^{\rm{c}}}) = 0$$ (5) $${f_3}({x^w},{y^w},{z^w},{u^{\rm{p}}}) = 0$$ (6) 式中：
${u^{\rm{c}}}$ 、${v^{\rm{c}}}$ 、${u^{\rm{p}}}$ 已知，由此，三维坐标$({x^w},{y^w},{z^w})$ 可以唯一求出。为了将深度学习进一步嵌入传统的测量流程，针对绝对相位到物体深度映射这一过程，文中提出了PDNet深度神经网络模型，该网络将物体绝对相位图作为网络输入，输出为物体深度，其主要模块及相关参数设置如表1所示，输入图像分辨率为496
$ \times $ 496，Out-F与Out-Res分别代表各层输出图层通道数与输出分辨率。表 1 PDNet主要模块及参数
Table 1. Main modules and parameters of PDNet
Layer Type Out-F Out-Res 1 Conv3d 16 3×496×496 2 ReLU 16 3×496×496 3 BatchNorm3d 16 3×496×496 4 Conv3d 32 3×496×496 5 ReLU 32 3×496×496 6 BatchNorm3d 32 3×496×496 7 Conv3d 64 3×496×496 8 ReLU 64 3×496×496 9 BatchNorm3d 64 3×496×496 10 Conv3d 128 3×496×496 11 ReLU 128 3×496×496 12 BatchNorm3d 128 3×496×496 13 Conv3d 64 3×496×496 14 ReLU 64 3×496×496 15 BatchNorm3d 64 3×496×496 16 Conv3d 32 3×496×496 17 ReLU 32 3×496×496 18 BatchNorm3d 32 3×496×496 19 Conv3d 1 1×496×496 20 ReLU 1 1×496×496 21 BatchNorm3d 1 1×496×496 -
能否直接由单帧条纹图学习三维深度值是深度学习三维测量领域备受关注的研究，但由于这种数据任务的复杂性和合理性，发表的相关工作极少。代表性工作是参考文献[12]，提出了一种单阶段网络进行三维测量的方法，使用一张条纹图作为深度神经网络的输入，通过网络直接获得物体的深度信息，其测量原理如图2所示。图2(a)为网络的输入，即单张条纹投影图，图2(b)为网络预测得到的物体深度。参考文献[12]分别采用FCN、AEN、UNet三种网络从单张条纹投影图获得物体深度信息，其中UNet的测量精度最高。单阶段深度学习单帧条纹投影三维测量方法能够帮助网络进行学习的数据只有输入的单幅条纹图和作为真值(Ground Truth)的深度，网络得到的信息量较少，单纯依靠数据驱动，缺少传统物理过程的约束和辅助。
图 2 单阶段深度学习单帧条纹投影三维测量方法。(a)条纹投影图；(b)UNet；(c)物体深度图
Figure 2. Single-stage deep learning based single-frame fringe projection 3D measurement method. (a)Fringe projection; (b)UNet; (c)Depth
-
文中联合FPTNet与PDNet，提出了一种多阶段深度学习单帧条纹投影三维测量方法。根据相移法及多频法测量过程，将端到端的单阶段网络学习步骤拆解为相位重建和深度映射两个阶段，同样是条纹图输入、深度值输出，满足端到端需求。令相移步数为
$N$ ，选用的条纹频率为${f_i} = {2^{i- 1}}$ ($i$ =1,2,…,s)，如图3所示。首先将$N$ 步相移条纹图的第一张（见图3(a)）作为FPTNet的输入，通过FPTNet变换生成s组频率呈指数增长的$N$ 张相移条纹（见图3(c)），之后，使用相移法及多频法进行相位计算与相位展开，获得频率为${f_s}$ 时的绝对相位（见图3(d)）。最后，将物体的绝对相位作为PDNet的输入，利用PDNet获得物体的深度信息（见图3(f)）。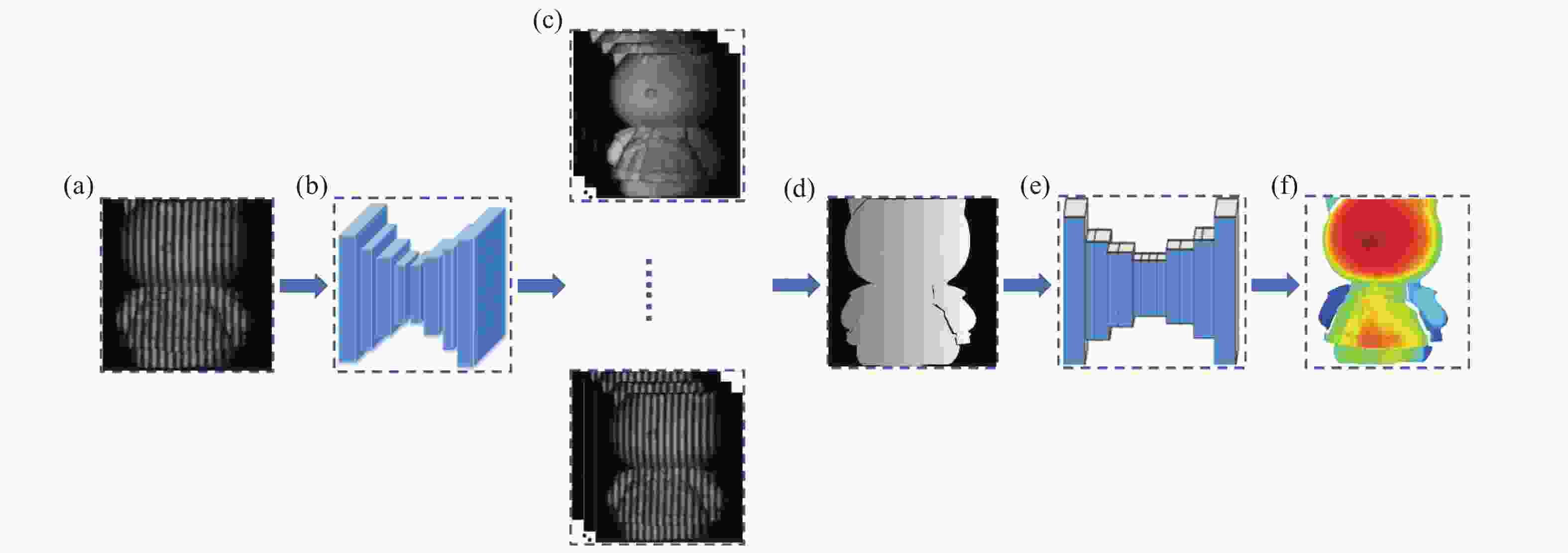
图 3 多阶段深度学习单帧条纹投影三维测量方法。(a) 条纹投影图；(b) FPTNet；(c) s组频率不同的相移条纹图；(d) 绝对相位；(e) PDNet；(f) 物体深度图
Figure 3. Multi-stage deep learning based single-frame fringe projection 3D measurement method. (a) Fringe; (b) FPTNet; (c) s phase-shifted fringe with different frequencies; (d) absolute phase; (e) PDNet; (f) depth
在多阶段深度学习单帧条纹投影三维测量方法中，FPTNet进行条纹变换以及PDNet进行相位深度映射时，分别将相机采集到的标准条纹图及物体的真实深度值作为FPTNet与PDNet的真值。相比于单阶段网络进行三维测量，这一过程更符合传统物理测量过程，且给予网络更多的信息量，增加了物理约束。
-
文中采用数字条纹投影三维测量技术获得了一组数据集，称之为Complex 3D，简称C3D数据集。在采集过程中，使用投影仪(DLP6500, Texas Instruments)进行条纹投影，采用CMOS相机(Basler acA800-510um，分辨率为800×600，焦距12 mm)进行图像拍摄。被测物体与实验装置间的距离在1 m左右，拍摄图像分辨率为496×496。为进行FPTNet的训练，获得更准确的相位值和深度值，文中向物体投影
$N$ =12，S=7，即频率为${f_i} = 2^{i- 1}$ ($i$ =1,2,…,7)的十二步相移条纹图，通过相机进行采集。继而，选用多频法对频率为${f_7}$ 的包裹相位进行相位展开，结合系统标定参数获得物体准确的相位和深度值作为真值。每组数据中训练集、验证集及测试集分别由50、20、20个真实场景所组成（数据样本不重复、结构多样性复杂性高，与目前主流的深度学习三维测量方法[10-11]的训练测试规模相当），分别用作训练网络、调整超参数与初步评估网络性能、评估最终网络的性能。文中所有的实验结果均在测试集上得到。 -
近年来，编码-解码结构深度神经网络经过不断发展，在参数量和结构复杂度上已经发生较大变化。为比较单阶段深度学习单帧条纹投影三维测量方法与多阶段深度学习单帧条纹投影三维测量方法在测量精度上的差异，同时降低网络类型对实验的影响，使用Deeplab V3+[14]、ERFNet[15]与UNet三种单阶段网络在C3D数据集上进行三维测量，其中Deeplab V3+、ERFNet与UNet在模型复杂度（文中用参数量表示，即网络中所有带参数层的权重参数总量，模型参数量与其计算复杂性正相关[16]，直接关系三维测量效率）与网络结构上各不相同。分别选取
${f_7}$ 的十二步相移条纹图的第一张作为网络输入，对应深度值作为网络真值，用三种网络进行三维测量。文中选用两组不同的数据，展示Deeplab V3+、ERFNet与UNet所获得的深度信息结果，如图4与图5所示。图4所示为一个平坦区域较多、深度阶跃不大且深度阶跃区域较少（称为简单形貌）的物体，网络输入如图4(a)所示，图4(f)为物体深度值的真值。图4(b)、4(c)、4(d)分别为Deeplab V3+、ERFNet、UNet的预测结果，将其与真值相减，得到预测结果的深度误差图，如图4(g)、4(h)、4(i)。可知，Deeplab V3+与ERFNet测量误差约为10 mm，并且存在大量的区域误差在20 mm以上，获得的三维数据已经无法反映物体的真实三维信息。而UNet测量误差约为6 mm，相比于Deeplab V3+与ERFNet精度得到了一定的提升。然而，部分区域的误差高于15 mm，甚至有些区域的误差超过了20 mm，这对于三维测量是难以接受的。
对于图5中平坦区域相对较少、深度阶跃大且深度阶跃区域较多（称为复杂形貌）的物体，三种网络测量的误差(图5(g)、5(h)、5(i))均达到10 mm以上，这表明，采用单阶段深度学习单帧条纹投影三维测量方法时，形貌复杂的物体已无法进行正确的形貌恢复。
图 4 两种方法对简单形貌物体进行三维测量结果。(a) 条纹投影图；(b) Deeplab V3+测量结果；(c) ERFNet测量结果；(d) UNet测量结果；(e) 文中方法测量结果；(f) 真值；(g) Deeplab V3+测量误差；(h) ERFNet测量误差；(i) UNet测量误差； (j)文中方法测量误差
Figure 4. 3D measurement results of two methods for a simple morphologic object. (a) Fringe projection; (b) measurement result of Deeplab V3+; (c) measurement result of ERFNet; (d) measurement result of UNet; (e) measurement result of the proposed method; (f) ground truth; (g) measurement error of DeeplabV3+; (h) measurement error of ERFNet; (i) measurement error of UNet; (j) measurement error of the proposed method
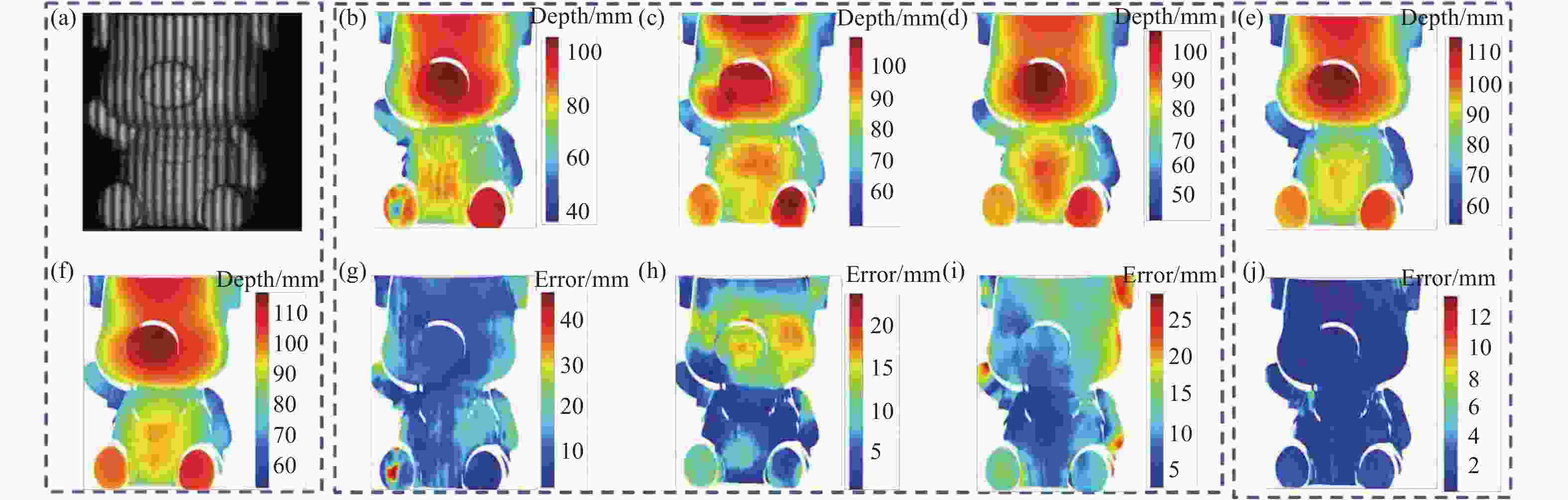
图 5 两种方法对复杂形貌物体进行三维测量结果。(a) 条纹投影图；(b) Deeplab V3+测量结果；(c) ERFNet测量结果；(d) UNet测量结果；(e) 文中方法测量结果；(f) 真值；(g) Deeplab V3+测量误差；(h) ERFNet测量误差；(i) UNet测量误差；(j) 文中方法测量误差
Figure 5. 3D measurement results of two methods for a complex morphologic object. (a) Fringe projection; (b) measurement result of Deeplab V3+; (c) measurement result of ERFNet; (d) measurement result of UNet; (e) measurement result of the proposed method; (f) ground truth; (g) measurement error of Deeplab V3+; (h) measurement error of ERFNet; (i) measurement error of UNet; (j) measurement error of the proposed method
-
同样使用C3D数据集，采用多阶段深度学习单帧条纹投影三维测量方法。首先选取
${f_7}$ 的十二步相移条纹图的第一张条纹图通过FPTNet变换生成${f_i} = 2^{i- 1}$ ($i$ =1,2,…,7)的十二张相移条纹图。之后，通过相移法进行相位计算及多频法进行相位展开得到物体的绝对相位。下一步，利用上述得到的绝对相位通过PDNet得到物体深度，结果如图4(e)与图5(e)所示。对于图4物体，从图4(j)中可见，使用多阶段深度学习单帧条纹投影三维测量方法时，其误差约为1 mm，精度得到明显提升，绝大部分区域的误差在2 mm以内，仅有部分边缘区域精度较低。对于图5物体，使用多阶段深度学习单帧条纹投影三维测量方法时，其误差(图5(j))在2 mm以下，相比单阶段深度学习单帧条纹投影三维测量方法，在形貌复杂的物体上具有更好的测量效果。文中通过计算测试集的误差RMSE对Deeplab V3+、ERFNet与UNet进行单阶段深度学习单帧条纹投影三维测量与多阶段深度学习单帧条纹投影三维测量所获得的结果进行评估，结果如表2所示。
表 2 两种方法的三维测量结果
Table 2. 3D measurement results of two methods
Method Network Input Parameters RMSE/mm Single-stage Deeplab V3+ f=64 single-frame fringe 59 350 673 9.605 ERFNet 2 063 922 9.018 UNet 34 528 769 6.911 Multi-stage FPTNet joint PDNet 14 508 785 1.408 从表2可见，多阶段深度学习单帧条纹投影三维测量方法的误差RMSE为1.408 mm，这一测量误差远远低于单阶段深度学习单帧条纹投影三维测量方法的结果。
为了进一步分析多阶段深度学习单帧条纹投影三维测量方法的测量误差分布，图6展示了使用该方法测量一个物体的误差图。图6(a)中包含深度阶跃形貌（红框区域）和平坦光滑形貌（绿框区域）的两个区域分别在图6(b)和图6(c)中被放大和重现，可以看出，误差主要集中在被测物体上的深度阶跃区域，测量误差可以达到3.5 mm，而平坦区域误差较小，测量误差一般小于0.6 mm。
图 6 (a) 多阶段深度学习单帧条纹投影三维测量方法的误差图；(b) (a)图红框中的放大细节；(c) (a)图绿框中的放大细节；
Figure 6. (a) Error of multi-stage deep learning based single-frame fringe projection 3D measurement method; (b) corresponding enlarged detail of the red box in (a); (c) corresponding enlarged detail of the green box in (a)
这是由于深度阶跃区域属于细节部分，文中方法第一阶段FPTNet属于Encoder-Decoder结构的深度神经网络。Encoder为了提取不同尺度特征进行下采样，但会丢失细节；Decoder进行上采样恢复细节，但丢失的细节难以完全恢复。此外，由于平坦区域在被测物体上占大部分，对损失函数的贡献更高，因此网络也倾向于把平坦区域学的更好。
综上，相比单阶段深度学习单帧条纹投影三维测量方法，多阶段深度学习单帧条纹投影三维测量方法结合了深度学习和物理测量过程，具有更高的测量精度；相比传统相移法，文中方法只需单帧条纹图即可进行三维测量，可实现快速测量，但在深度阶跃区域，测量效果仍有待提升。
后续笔者等将考虑设计更合理的网络，加强恢复细节，同时优化损失函数，增强网络在深度阶跃区域的表现。
-
在多阶段深度学习单帧条纹投影三维测量方法中，误差分为两部分。第一部分通过FPTNet获得绝对相位会引入一定的误差，为了分析该步骤对最终获得的深度误差造成的影响，在C3D数据集中进行了如下实验。首先，对相机采集到的条纹图像进行相位恢复，得到标准绝对相位，随后，将标准的绝对相位与通过FPTNet得到的绝对相位分别作为输入，得到实际物体的深度，结果如表3所示。由表3可见，使用标准相位进行深度估计时，深度误差得到了明显降低，在C3D数据集的测试集上RMSE仅为0.493 mm。这说明，FPTNet引起的相位偏差是多阶段深度学习单帧条纹投影三维测量方法的主要误差来源。
表 3 多阶段深度学习单帧条纹投影三维测量方法在C3D测试集上的误差
Table 3. Error of multi-stage deep learning based single-frame fringe projection 3D measurement method on C3D test set
Input Method RMSE/mm Correct absolute phase PDNet 0.493 Absolute phase obtained by FPTNet 1.408 第二部分为PDNet进行绝对相位到深度映射时产生的误差。为验证PDNet精度，文中在C3D数据集中对直径为25.4 mm的标准球进行了采集，对于计算得到的绝对相位，分别通过标定参数方法与PDNet测量标准球的深度。对两种方法得到的深度数据进行球面拟合，对比拟合误差，结果如表4所示。可以看到使用标定参数将绝对相位映射到深度的方法能达到的精度为0.018 mm，使用PDNet的精度为0.363 mm（由于标准球结构简单，其误差小于表3中C3D数据集测试集的平均水平）。
表 4 标定参数方法与PDNet测量标准球的精度
Table 4. Accuracy of measuring the standard sphere by using calibration parameter and PDNet
Input Method RMSE/mm Absolute phase Using calibration parameters 0.018 PDNet 0.363 这些实验表明，尽管精度低于标定参数方法，但PDNet的测量精度已达到亚毫米级，证明将深度学习用于绝对相位到深度的映射具有可行性；降低FPTNet阶段的条纹图预测偏差导致的相位偏差，可大幅提升多阶段深度学习单帧条纹投影三维测量方法精度。
-
文中提出了一种PDNet深度神经网络模型用于进行绝对相位到深度的映射，并将FPTNet与PDNet联合，提出了一种多阶段深度学习单帧条纹投影三维测量方法。多阶段深度学习单帧条纹投影三维测量方法在复杂数据集上平均测量误差为1.408 mm，与单阶段深度学习单帧条纹投影三维测量方法的误差6.911 mm相比明显下降，测量误差降低了约4倍。结果表明，舍弃传统的物理过程，采用单阶段网络直接从单幅条纹图像获得物体的三维形貌的方法增加了网络学习的难度。为获得更高精度的三维形貌测量结果，需结合深度学习和物理测量过程，分阶段将深度学习融入传统的计算流程中，给予网络更多物理过程约束。笔者等后续将继续研究该思想在计算三维测量中的应用，进一步提高测量精度。此外，PDNet的提出证明了使用深度学习实现三维测量中绝对相位映射深度步骤的可行性，标准球验证精度可达0.363 mm，为后续使用深度神经网络进行标定参数等系数的优化提供了参考，也证明了将深度神经网络全面应用于数字条纹投影三维测量的可能性。
Multi-stage deep learning based single-frame fringe projection 3D measurement method
-
摘要:
深度学习的应用简化了数字条纹投影三维测量的过程，在传统数字条纹投影三维测量技术条纹投影、相位计算、相位展开、相位深度映射的流程中，研究者们已经成功证明了前三个环节以及整个流程结合深度神经网络的可行性。基于深度学习，PDNet (Phase to Depth Network)神经网络模型被提出，用于绝对相位到深度的映射。结合多阶段深度学习单帧条纹投影三维测量方法，通过分阶段学习方式依次获得物体的绝对相位与深度信息。实验结果表明，PDNet能较准确地测量出物体的深度信息，深度学习应用于相位深度映射步骤具有可行性。并且，相较于直接从条纹图像到三维形貌的单阶段深度学习单帧条纹投影三维测量方法，多阶段深度学习单帧条纹投影三维测量方法可以明显提升测量精度，仅需单帧条纹图像输入即可获得毫米级测量精度，且能适应具有复杂形貌物体的三维测量。
Abstract:The application of deep learning has simplified the process of 3D measurement of digital fringe projection. In the process of fringe projection, phase calculation, phase unwrapping, and phase-depth mapping of traditional digital fringe projection 3D measurement technology, researchers have successfully demonstrated the feasibility of combining the first three stages and the entire process with deep neural networks. Based on deep learning, the Phase to Depth Network (PDNet) was proposed to achieve the map from absolute phase to depth. Combined with multi-stage deep learning based single-frame fringe projection 3D measurement method, the absolute phase and depth information of the object were obtained by deep learning in stages. The experimental results show that the PDNet can measure the depth information of the object comparatively accurately, and the application of deep learning is feasible in the phase-height mapping stage. And compared with the single-stage deep learning based single-frame fringe projection 3D measurement method that directly maps from the fringe image to the three-dimensional topography information, multi-stage deep learning based single-frame fringe projection 3D measurement method can significantly improve the measurement accuracy, which only require a single fringe input to obtain millimeter-level measurement accuracy, and it can adapt to 3D measurement of objects with complex surfaces.
-
Key words:
- digital fringe projection /
- deep learning /
- multi-stage deep learning /
- 3D measurement
-
图 1 传统数字条纹投影方法进行三维测量。(a) 条纹投影图；(b) 包裹相位；(c) 绝对相位；(d) 物体深度图
Figure 1. 3D measurement of traditional digital fringe projection. (a) Fringe projection; (b) wrapped phase; (c) absolute phase; (d) depth
图 2 单阶段深度学习单帧条纹投影三维测量方法。(a)条纹投影图；(b)UNet；(c)物体深度图
Figure 2. Single-stage deep learning based single-frame fringe projection 3D measurement method. (a)Fringe projection; (b)UNet; (c)Depth
图 3 多阶段深度学习单帧条纹投影三维测量方法。(a) 条纹投影图；(b) FPTNet；(c) s组频率不同的相移条纹图；(d) 绝对相位；(e) PDNet；(f) 物体深度图
Figure 3. Multi-stage deep learning based single-frame fringe projection 3D measurement method. (a) Fringe; (b) FPTNet; (c) s phase-shifted fringe with different frequencies; (d) absolute phase; (e) PDNet; (f) depth
图 4 两种方法对简单形貌物体进行三维测量结果。(a) 条纹投影图；(b) Deeplab V3+测量结果；(c) ERFNet测量结果；(d) UNet测量结果；(e) 文中方法测量结果；(f) 真值；(g) Deeplab V3+测量误差；(h) ERFNet测量误差；(i) UNet测量误差； (j)文中方法测量误差
Figure 4. 3D measurement results of two methods for a simple morphologic object. (a) Fringe projection; (b) measurement result of Deeplab V3+; (c) measurement result of ERFNet; (d) measurement result of UNet; (e) measurement result of the proposed method; (f) ground truth; (g) measurement error of DeeplabV3+; (h) measurement error of ERFNet; (i) measurement error of UNet; (j) measurement error of the proposed method
图 5 两种方法对复杂形貌物体进行三维测量结果。(a) 条纹投影图；(b) Deeplab V3+测量结果；(c) ERFNet测量结果；(d) UNet测量结果；(e) 文中方法测量结果；(f) 真值；(g) Deeplab V3+测量误差；(h) ERFNet测量误差；(i) UNet测量误差；(j) 文中方法测量误差
Figure 5. 3D measurement results of two methods for a complex morphologic object. (a) Fringe projection; (b) measurement result of Deeplab V3+; (c) measurement result of ERFNet; (d) measurement result of UNet; (e) measurement result of the proposed method; (f) ground truth; (g) measurement error of Deeplab V3+; (h) measurement error of ERFNet; (i) measurement error of UNet; (j) measurement error of the proposed method
图 6 (a) 多阶段深度学习单帧条纹投影三维测量方法的误差图；(b) (a)图红框中的放大细节；(c) (a)图绿框中的放大细节；
Figure 6. (a) Error of multi-stage deep learning based single-frame fringe projection 3D measurement method; (b) corresponding enlarged detail of the red box in (a); (c) corresponding enlarged detail of the green box in (a)
表 1 PDNet主要模块及参数
Table 1. Main modules and parameters of PDNet
Layer Type Out-F Out-Res 1 Conv3d 16 3×496×496 2 ReLU 16 3×496×496 3 BatchNorm3d 16 3×496×496 4 Conv3d 32 3×496×496 5 ReLU 32 3×496×496 6 BatchNorm3d 32 3×496×496 7 Conv3d 64 3×496×496 8 ReLU 64 3×496×496 9 BatchNorm3d 64 3×496×496 10 Conv3d 128 3×496×496 11 ReLU 128 3×496×496 12 BatchNorm3d 128 3×496×496 13 Conv3d 64 3×496×496 14 ReLU 64 3×496×496 15 BatchNorm3d 64 3×496×496 16 Conv3d 32 3×496×496 17 ReLU 32 3×496×496 18 BatchNorm3d 32 3×496×496 19 Conv3d 1 1×496×496 20 ReLU 1 1×496×496 21 BatchNorm3d 1 1×496×496 
下载: 导出CSV
表 2 两种方法的三维测量结果
Table 2. 3D measurement results of two methods
Method Network Input Parameters RMSE/mm Single-stage Deeplab V3+ f=64 single-frame fringe 59 350 673 9.605 ERFNet 2 063 922 9.018 UNet 34 528 769 6.911 Multi-stage FPTNet joint PDNet 14 508 785 1.408
下载: 导出CSV
表 3 多阶段深度学习单帧条纹投影三维测量方法在C3D测试集上的误差
Table 3. Error of multi-stage deep learning based single-frame fringe projection 3D measurement method on C3D test set
Input Method RMSE/mm Correct absolute phase PDNet 0.493 Absolute phase obtained by FPTNet 1.408
下载: 导出CSV
表 4 标定参数方法与PDNet测量标准球的精度
Table 4. Accuracy of measuring the standard sphere by using calibration parameter and PDNet
Input Method RMSE/mm Absolute phase Using calibration parameters 0.018 PDNet 0.363
下载: 导出CSV
-
[1] Yu Xiaoyang, He Jialuan, Huang Ming. et al. Colouring of 3D reconstructed surfaces of structure light based on coloured images [J]. Opt Precision Eng, 2009, 17(10): 2561−2568. (in Chinese) doi: 10.3321/j.issn:1004-924X.2009.10.032 [2] Song Zhan, Ronald Chung. Determining both surface position and orientation in structured- light-based sensing [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(10): 1770−1780. doi: 10.1109/TPAMI.2009.192 [3] Chen Xiaorong, Cai Ping, Shi Wenkang. The latest development of optical noncontact 3D profile measurement [J]. Opt Precision Eng, 2002, 10(5): 528−532. (in Chinese) doi: 10.3321/j.issn:1004-924X.2002.05.001 [4] Wang Jianhua, Yang Yanxi. Double N-step phase-shifting profilometry using color-encoded grating projection [J]. Chinese Optics, 2019, 12(3): 616−627. (in Chinese) [5] Zhao Yalong, Liu Shouqi, Zhang Qican. 3D shape measurement accelerated by GPU [J]. Infrared and Laser Engineering, 2018, 47(3): 0317003. (in Chinese) [6] Lu Feng, Wu Chengdong, Jia Tong, et al. Phase unwrapping based on two types ofstair-mode [J]. Infrared and Laser Engineering, 2018, 47(8): 0826002. doi: 10.3788/IRLA201847.0826002 [7] Zheng Dongliang, Da Feipeng, Kemao Qian, et al. Phase-shifting profilometry combined with Gray-code patterns projection: Unwrapping error removal by an adaptive median filter [J]. Optics Express, 2017, 25(5): 4700. doi: 10.1364/OE.25.004700 [8] Zuo Chao, Huang Lei, Zhang Minliang, et al. Temporal phase unwrapping algorithms for fringe projection profilometry: A comparative review [J]. Optics and Lasers in Engineering, 2016, 85: 84−103. doi: 10.1016/j.optlaseng.2016.04.022 [9] Yu Haotian, Chen XiaoyuX, Zhang Zhao, et al. Dynamic 3-D measurement based on fringe-to-fringe transformation using deep learning[EB/OL]. [2019-12-30]. https://arxiv.org/abs/1906.05652. [10] Feng Shijie, Zuo Chao, Yin Wei, et al. Micro deep learning profilometry for high-speed 3D surface imaging [J]. Optics and Lasers in Engineering, 2019, 121: 416−427. doi: 10.1016/j.optlaseng.2019.04.020 [11] Yin Wei, Chen Qian, Feng Shijie, et al. Temporal phase unwrapping using deep learning[EB/OL]. [2019-5-28]. https://arxiv.org/abs/1903.09836. [12] Nguyen H, Li Hui, Qiu Qiang, et al. Single-shot 3d shape reconstruction using deep convolutional neural networks[EB/OL]. [2019-9-17]. https://arxiv.org/abs/1909.07766. [13] An Dong, Chen Li, Ding Yifei, et al. Optical system model and calibration of grating projection phase method [J]. Chinese Optics, 2015, 8(2): 248−254. doi: 10.3788/co.20150802.0248 [14] Chen Liang-Chieh, Zhu Yukun, George Papandreou, et al. Encoder-decoder with atrous separable convolution for semantic image segmentation[EB/OL]. [2018-8-22]. https://arxiv.org/abs/1802.02611. [15] Romera E, Alvarez J M, Bergasa L M, et al. ERFNet: Efficient residual factorized ConvNet for real-time semantic segmentation [J]. IEEE Transactions on Intelligent Transportation Systems, 2018, 19(1): 263−272. doi: 10.1109/TITS.2017.2750080 [16] Zhang Chen, Li Peng, Sun Guangyu, et al. Optimizing FPGA-based accelerator design for deep convolutional neural networks[C]//Proceedings of the 2015 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays. ACM, 2015: 161-170. -
点击查看大图
计量
- 文章访问数: 648
- HTML全文浏览量: 140
- 被引次数: 0
