-
光纤激光器尤其是以小型整机化为目标的高功率光纤激光系统,结合了当今最新的高亮度半导体激光技术、热控管理技术、高性能掺杂光纤拉制技术以及光纤光栅等无源器件的制作技术为一体的综合技术,已经成为当今光电子技术领域最灸手可热的研究方向之一。高功率光纤激光具有光束质量好、输出效率高、结构紧凑易维护等显著优点,已经广泛应用于工业制造、科学研究和军事国防等诸多领域[1-3]。光纤的波导结构使其在数千瓦级高功率运转的情况下仍能保持输出光束近衍射极限的特性,但由于光纤本身的长度长、横截面积小、热传导性能有限,将功率量级如此之高的激光限制在微米量级纤细的光纤中,可能会引发各种非线性效应降低激光器的输出性能。
研究人员普遍认为采用大模场光纤似乎是解决这类问题最显而易见的方法[4]。然而,大模场光纤的频繁使用又会引发出新的问题,模场直径的扩展使得激光器难以维持单横模运转,会不断激发出高阶模的震荡,劣化输出的光束质量,更有甚者,在高功率运转下可能会进一步诱发横模不稳定(TMI)现象的发生,导致输出亮度严重下降[5-6]。这一现象已经成为限制近衍射极限激光器输出功率持续提升的首要瓶颈问题,是当前高功率光纤激光发展中亟待解决的技术难题。
文中基于常规的大模场光纤25/400 μm构建了高功率全光纤化的主振荡功率放大(MOPA)平台,对窄线宽大模场光纤激光器中的TMI效应进行了多维度的探索研究。理论上,通过模式耦合的相互作用分析了25/400 μm光纤中基模LP01跟各高阶模之间的非线性耦合系数,结果表明,次高阶模LP11和基模LP01之间的耦合作用最强,最大耦合频率处于3 kHz附近。与此同时,基于LP01模和LP11模之间的非线性耦合强度以及弯曲限模的损耗系数,简要评估出了不同弯曲半径条件下光纤激光系统的TMI阈值大小。当大模场光纤25/400 μm的弯曲半径从6.5 cm缩小至4.5 cm,理论评估的结果显示TMI的阈值范围可从300 W量级提升到4000 W量级。实验上,通过改变主放大级增益光纤的弯曲半径,从时域、频域和功率等多个方面验证了TMI效应的发生,最终探测到高功率光纤激光系统的TMI阈值从1000 W量级提升到了1600 W量级。理论和实验双方面的研究结果都表明弯曲限模可有效抑制大模场光纤中TMI现象的发生,利用此种普适性好、可操作性强的模式滤波方法,可实现对TMI阈值的有效提高,有助于推动窄线宽高功率全光纤激光系统的工程化发展。
-
自2010年德国Jena大学[7]首次观测到TMI现象以来,科研人员对其展开了大量的研究探索,已经逐步发展出多种不同的物理模型来描述TMI[6, 8-12]。目前,研究人员普遍认为高功率光纤激光中TMI发生的根源在于量子亏损引起的热效应以及大模场光纤纤芯支持多个传输模式。当信号光注入大模场光纤时,虽然插入了模场适配器来过渡,仍然会不可避免地激发少量的高阶模式[13]。基模和高阶模沿着光纤的轴向进行传输,纵向的模间干涉效应会诱发增益光纤中不同位置的反转粒子数呈周期性分布。上能级反转粒子数的分布与光纤放大器中的增益系数相对应,并直接影响量子损耗导致的热沉积,通过热光效应,调制光纤折射率分布呈周期性变化。该周期满足光栅的相位匹配条件,因而可以实现基模和高阶模之间的能量耦合[14]。
文中基于丹麦科技大学Hansen等[8, 15]建立的半解析理论模型,分析了大模场光纤中各高阶模成分与基模LP01之间的非线性耦合作用,从而简要评估出光纤激光系统在不同弯曲半径下的TMI阈值大小。输出激光中的高阶模成分是评价激光模式特性的重要指标之一。因此,引入高阶模成分占比
$\xi $ 来量化评价TMI现象,$\xi (L)$ 可以定义为:$$\xi (L) = \dfrac{{{P_2}(L)}}{{{P_1}(L) + {P_2}(L)}}$$ (1) 式中:
${P_2}$ 为高阶模输出功率;${P_1}$ 为基模输出功率。文中的理论模型主要研究量子噪声和注入信号光的强度噪声等[16]诱发的TMI效应。当初始入射的信号光中只有基模而无任何高阶模成分时,TMI现象的发生主要由量子噪声(
$\hbar {\omega _0}$ )引起,此时高阶模的成分占比$\xi (L)$ 可表示为:$$\xi (L) \approx \dfrac{{\hbar {\omega _0}\sqrt {\dfrac{{2\pi {\varGamma _1}}}{{\left| {\chi ''({\Omega _p})} \right|}}} \dfrac{{{P_1}{{(L)}^{({\varGamma _2}/{\varGamma _1} - 3/2)}}}}{{{P_{0,1}}^{{\varGamma _2}/{\varGamma _1}}}}\exp \Bigg[\dfrac{{\chi ({\Omega _p})}}{{{\varGamma _1}}}({P_1}(L) - {P_{0,1}})\Bigg]{\rm{exp( - }}{\alpha _{{\rm{coil}}}}{L_{{\rm{coil}}}}{\rm{)}}}}{{1{\rm{ + }}\hbar {\omega _0}\sqrt {\dfrac{{2\pi {\varGamma _1}}}{{\left| {\chi ''({\Omega _p})} \right|}}} \dfrac{{{P_1}{{(L)}^{({\varGamma _2}/{\varGamma _1} - 3/2)}}}}{{{P_{0,1}}^{{\varGamma _2}/{\varGamma _1}}}}\exp \Bigg[\dfrac{{\chi ({\Omega _p})}}{{{\varGamma _1}}}({P_1}(L) - {P_{0,1}})\Bigg]{\rm{exp( - }}{\alpha _{{\rm{coil}}}}{L_{{\rm{coil}}}}{\rm{)}}}}$$ (2) 而当初始入射的信号光中原本就有高阶模(
$\xi (0)$ )存在时,输入信号光的强度噪声也会诱发TMI效应,此时高阶模的成分占比$\xi (L)$ 可表示为:$$\xi (L) \approx \dfrac{{\xi (0){{\left[ {\dfrac{{{P_{0,1}}}}{{{P_1}(L)}}} \right]}^{1 - \dfrac{{{\varGamma _2}}}{{{\varGamma _1}}}}}\left\{ {1 + \dfrac{1}{4}{R_N}({\Omega _p})\sqrt {\dfrac{{2\pi {\varGamma _1}}}{{{P_1}(L)\left| {\chi ''({\Omega _p})} \right|}}} } \right.\left. {\exp \Bigg[\dfrac{{\chi ({\Omega _p})}}{{{\varGamma _1}}}({P_1}(L) - {P_{0,1}})\Bigg]} \right\}{\rm{exp( - }}{\alpha _{{\rm{coil}}}}{L_{{\rm{coil}}}}{\rm{)}}}}{{1{\rm{ + }}\xi (0){{\left[ {\dfrac{{{P_{0,1}}}}{{{P_1}(L)}}} \right]}^{1 - \dfrac{{{\varGamma _2}}}{{{\varGamma _1}}}}}\left\{ {1 + \dfrac{1}{4}{R_N}({\Omega _p})\sqrt {\dfrac{{2\pi {\varGamma _1}}}{{{P_1}(L)\left| {\chi ''({\Omega _p})} \right|}}} } \right.\left. {\exp \Bigg[\dfrac{{\chi ({\Omega _p})}}{{{\varGamma _1}}}({P_1}(L) - {P_{0,1}})\Bigg]} \right\}{\rm{exp( - }}{\alpha _{{\rm{coil}}}}{L_{{\rm{coil}}}}{\rm{)}}}}$$ (3) 其中,
$$\chi (\Omega ) = 2\pi \dfrac{{\eta ({\lambda _s} - {\lambda _p})}}{{\kappa {n_c}{\lambda _s}{\lambda _p}}}{\rm{Im}} [{G_{2121}}(\Omega )]$$ (4) $$\begin{aligned} {G_{2121}}(\Omega ) = & \pi \displaystyle\int_0^b {{R_1}(r)} {R_2}(r)r\int_0^a {{R_1}(r')} \times {\rm{ }}{R_2}(r'){{\rm{g}}_1}(r,r',\Omega )r'{\rm{d}}r'{\rm{d}}r \\ \end{aligned} $$ (5) $$ {{{g}}_1}(r,r',\Omega ){\rm{ = }}\left\{ {\begin{array}{*{20}{c}} {{I_1}(\sqrt q r)[\dfrac{{{K_2}(\sqrt q b) + {K_0}(\sqrt q b) - A{K_1}(\sqrt q b)}}{{{I_2}(\sqrt q b) + {I_0}(\sqrt q b) + A{I_1}(\sqrt q b)}}{I_1}(\sqrt q r') + {K_1}(\sqrt q r')]\;\;\;{\rm{ 0}} \leqslant r < r'}\\ {{I_1}(\sqrt q r')[\dfrac{{{K_2}(\sqrt q b) + {K_0}(\sqrt q b) - A{K_1}(\sqrt q b)}}{{{I_2}(\sqrt q b) + {I_0}(\sqrt q b) + A{I_1}(\sqrt q b)}}{I_1}(\sqrt q r) + {K_1}(\sqrt q r)]\;\;\;r' \leqslant r < b} \end{array}} \right. $$ (6) 式中:
$\chi (\Omega )$ 是传输模式间的非线性耦合系数;${\Omega _p}$ 是$\chi (\Omega )$ 最大值所对应的频率;${R_N}({\Omega _p})$ 是相对强度噪声;变量q和A的指代形式分别为$i\rho C\Omega /\kappa $ 和$2{h_q}/\sqrt q \kappa $ ;函数In和Kn (n=0, 1, 2)则分别是第一类和第二类修正的贝塞尔函数;a和b是光纤的纤芯半径和外轮廓半径;${P_{0,\;1}}$ 为初始注入的信号功率;${\varGamma _1}$ 和${\varGamma _2}$ 为对应耦合模式成分的重叠因子;${\alpha _{{\rm{coil}}}}$ 是高阶模的损耗系数;${L_{{\rm{coil}}}}$ 是弯曲光纤的长度。根据Marcuse光纤弯曲的损耗理论[17],可分别计算出各传输模式在不同弯曲半径下的损耗系数,弯曲损耗的表达式如下:$${\alpha _{\rm{R}}} = \dfrac{{\sqrt \pi {U^2}\exp \left( - \dfrac{{2{W^3}}}{{3{a^3}{\beta ^2}}}R\right)}}{{2{e_\nu }{W^{3/2}}\sqrt {aR} {V^2}{K_{\nu - 1}}(W){K_{\nu + 1}}(W)}}$$ (7) 其中,
$${e_\nu } = \left\{ {\begin{array}{*{20}{c}} {2\;\;\;\;\;\;\nu {\rm{ = 0}}} \\ {1\;\;\;\;\;\;\nu \ne 0} \end{array}} \right.$$ (8) $${V^2} = {U^2}{\rm{ + }}{W^2}$$ (9) 式中:R是光纤的弯曲半径;
$\beta $ 是纵向传播常数;V、U和W分别是归一化工作频率、横向相位参数和衰减参数。利用大模场光纤25/400 μm的基本参数:NA=0.06,V=4.43@1064 nm,可分别计算出各传输模式在不同弯曲半径下的损耗系数,如图1所示。对比高阶模的弯曲损耗,图中基模LP01的损耗系数较小,两者之间存在着数量级的差别。因此,在理论评估光纤激光系统TMI阈值大小的时候,仅考虑增加了高阶模的弯曲损耗,而忽略了基模能量的损耗衰减,这也与参考文献[18]中的简化方式相一致。
图 1 25/400 μm光纤中各模式的损耗系数与弯曲半径的变化关系
Figure 1. The relationship between the loss coefficient and bend radius for the modes of a 25/400 μm fiber
根据表1所示的光纤激光的系统参数,并通过利用公式(4)~(6),可模拟仿真出大模场光纤25/400 μm中各高阶模成分与基模LP01之间的非线性耦合系数,数值计算结果如图2所示。从图中可以明显看出,相较于截止频率(
${V_c} = 3.8$ )较高的模式LP02和LP21,次高阶模LP11(${V_c} = 2.4$ )与基模LP01之间的耦合强度最高,所以高功率光纤激光系统中TMI效应的发生总是最先建立在这两个模式间的能量耦合和转换。表 1 光纤激光系统的参数设置
Table 1. Parameters of fiber laser system
Parameter Value Parameter Value ${n_c}$ 1.45 $b$ 300 μm $\kappa $ 1.4 W/(m·K) $\eta $ 3.5×10−5 K−1 ${h_q}$ 1000 W/(m2·K) $\rho C$ 1.67×106 J/(m3·K) ${\lambda _p}$ 976 nm ${\lambda _s}$ 1064 nm 
图 2 25/400 μm光纤中基模LP01与不同高阶模之间的非线性耦合系数
Figure 2. Nonlinear coupling coefficient between fundamental mode LP01 and different high order modes in 25/400 μm fiber
基于LP01模和次高阶模LP11两者之间的非线性耦合作用,代入计算公式(2)和(3),可分别有效评估出不同弯曲半径下高阶模成分占比的变化趋势。计算过程中,当
$\xi (L) = 0.05$ 时,即认为发生了横模不稳定现象,此时${P_1}$ 对应的功率量级即为TMI出现的阈值功率[8, 15]。当信号光中无高阶模成分存在时,TMI由光纤中的量子噪声引起,初始注入的信号功率
${P_{0,1}} = 17\;{\rm{ W}}$ ,不同弯曲半径条件下光纤激光器TMI阈值功率的变化趋势如图3(a)所示。而图3(b)描述的则是信号光中强度噪声引起的TMI效应,初始高阶模的成分占比为1%,即$\xi (0) = 0.01$ ,强度噪声的大小取为${R_N} = $ $ {10^{{\rm{ - 1}}3}}{\rm{H}}{{\rm{z}}^{-1}}$ 。对比两种不同诱因导致的TMI效应,不管是同一弯曲半径下TMI阈值的量级,还是不同弯曲半径对TMI阈值大小的影响,数值模拟的计算结果都基本类似。由图3可知,当大模场光纤25/400 μm的弯曲半径从6.5 cm缩小至4.5 cm的过程中,表1所示光纤激光系统的TMI阈值范围近似可从300 W量级提升到4000 W量级,直观说明了弯曲限模对TMI现象的有效抑制,得到不同弯曲半径条件下光纤激光系统的TMI阈值大小。 -
为了进一步研究全光纤窄线宽高功率光纤激光器中的TMI现象,文中搭建了级联的MOPA实验平台,具体的结构如图4所示。中心波长为1064 nm的单频激光器通过相位调制的方式将线宽展宽至50 GHz,以避免高功率放大过程中产生的非线性效应。种子激光经三级预放后,输出功率被提升至17 W,激光信噪比高达50 dB以上。为了避免后向回光对前级系统带来的危害,一个高功率的环形器(OC)被插入到预放级和主放大级之间,环形器的3端口级联了分束比不同的光纤型TAP,用以在线实时监测反向传输Stokes光的功率、时域和光谱的变化情况。非保偏的模场适配器(MFA)熔接在环形器和合束器之间来实现不同光纤类型的模场匹配,多模的半导体激光器经(6+1)×1的高功率合束器耦合注入到增益光纤中。主功率放大级的增益光纤选用的是Nufern公司纤芯直径25 μm,包层直径400 μm的非保偏双包层大模场光纤。该增益光纤的吸收系数约为0.6 dB/m@915 nm,为保证足够的泵浦吸收并有效降低非线性效应的积累,增益光纤的长度选定为6.5 m。自制的高功率包层光滤除器被熔接在增益纤之后,将双包层光纤中残余的泵浦光和包层激光剥除,输出端面切8°斜角防止端面反射产生的寄生振荡。为了验证弯曲限模对TMI阈值的有效提高,我们人为选取了两个中间的典型弯曲半径(
$R = 6\;{\rm{ cm }}\;\&\;R{\rm{ = 5\; cm}}$ )进行相关的实验探索,而且这两种弯曲半径也是高功率全光纤放大器实验平台的常规之选,在实际的工程应用中被频繁使用,具有更强的指导意义。 -
高功率光纤激光器中TMI现象的发生具有“阈值性”,当激光输出功率达到某个阈值后,光纤激光的输出模式由稳定的基模变为和高阶模相对成分随时间迅速变化的非稳定模式[2]。不同于其他常见的非线性效应,光纤激光中TMI的阈值和输出激光的平均功率有关,而与脉冲的峰值功率无关[19]。这些典型的特征将有助于对TMI现象的判定,是开展一系列实验研究的基础。
为了有效降低弯曲限模导致的功率损耗,确保激光器输出的斜率效率,首先将增益光纤的弯曲半径限定为6 cm,此时LP11模对应的损耗系数约为7.3 m−1。在泵浦功率不断增加的过程中,利用带宽150 MHz的光电探测器(PD)来实时采样输出激光功率的变化情况,如图5所示。当泵浦电流为4 A (633 W)和5 A (825 W)时,光电探测器输出的电压信号基本保持不变,产生的轻微扰动主要是由外界环境变化导致的低频噪声和激光器本底的功率噪声叠加而成。随着输出功率的进一步增长,除了电压信号的幅值会增加,对应的扰动信号也会相应增强,但此时的信号变化是杂乱无序的。当发生TMI现象后,光电探测器的电压信号会发生ms尺度的快速周期变化,而且随着输出功率的持续提升,周期性波形变得越来越明显,在输出功率达到1082 W时呈现出显著的类正弦周期波形,时间周期约为0.33 ms,对应的变化频率约为3 kHz。为进一步加强验证TMI现象的周期性行为,在时域变化特性的基础上,又对采集到的光信号进行了频谱分析,对应泵浦电流下的输出结果如图5(b)所示。通过测量信号的频谱分析可以明显看出,当泵浦电流加至6 A(1028 W)时,输出激光的功率噪声明显增大,特别是在3 kHz附近出现了显著增长,进一步增加泵浦电流至6.4 A和6.5 A时频谱信号在3 kHz处出现尖峰,对应于时域信号中周期性的振荡,这些探测到的典型变化特征都符合前文有关模式耦合效应的描述,也与参考文献[20]中观察到的实验现象一致。因此,针对现有大模场面积的25/400 μm增益光纤,当弯曲限模的半径设定在6 cm时,TMI的阈值处于1000 W量级。

图 5 弯曲半径为6 cm时输出激光采样到的(a)时域信号和(b)频域信号
Figure 5. (a) Time domain and (b) frequency domain variables sampled by the output laser when the bending radius is 6 cm
为进一步抑制TMI现象的发生,增益光纤的弯曲半径被缩小至5 cm,此时LP11模对应的弯曲损耗系数约为36.3 m−1,相较前文的7.3 m−1提高了5倍之多,有望实现更佳的模式滤波效果。在泵浦功率不断增加的过程中,探测到的时域和频率变化结果如图6所示,此处仅采样了TMI阈值附近的光信号变化。同样,当泵浦电流增加至11 A (1574 W)时,采样到的时域信号开始出现类周期性的振荡,但变化规律并不是很明显。进一步增加泵浦电流至11.4 A (1567 W),对应的时域信号变化也开始呈现出明显的正弦周期波形,但振荡的时间周期却发生了微弱的变化,约为0.4 ms,对应的振荡频率为2.5 kHz。这可能是因为弯曲半径的不同而导致了不同程度的模场畸变,使高阶模和基模间的耦合频率产生了微弱的变化。图6(b)给出了对应的频域变换结果,从图中依然可以明显的看到,随着泵浦电流的不断增加,频域信号在2.5 kHz附近的信号峰不断增强,进一步有效证实了TMI现象的发生。因此,当增益光纤的弯曲半径缩小至5 cm时,TMI的阈值功率被提高到了1600 W量级。
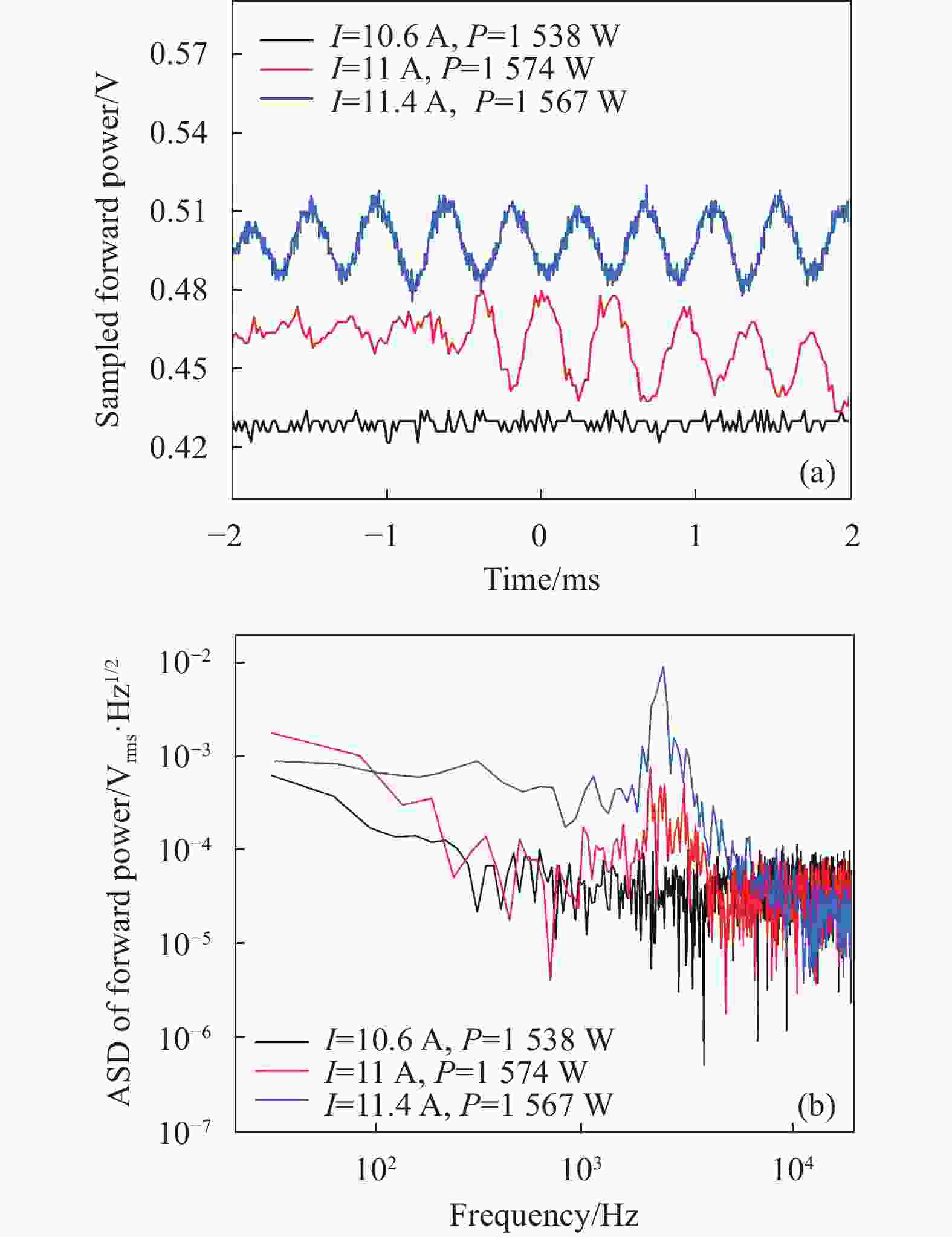
图 6 弯曲半径为5 cm时输出激光采样到的(a)时域信号和(b)频域信号
Figure 6. (a) Time domain and (b) frequency domain variables sampled by the output laser when the bending radius is 5 cm
两种弯曲半径下输出功率随泵浦功率的变化曲线如图7所示。从图中可以看出,当TMI现象发生后,输出激光功率都出现了类似的滞长现象,此时的功率损耗主要集中于泵浦滤除,对应器件的表面温度也会因此而急剧上升,这些现象的发生同样符合TMI的典型实验特征,有助于进一步确认TMI的阈值大小。对比两种运转模式的斜率效率略有差别,弯曲半径为6 cm的斜率效率82.7%略高于弯曲半径5 cm时的斜率效率81.8%。这主要是因为弯曲半径的不同,导致各模式成分的弯曲损耗差异显著,但基模LP01的整体弯曲损耗都相对较小,所以对基模为主的主能量激光输出影响并不明显,两者之间只偏差了1%,几乎可以认定弯曲半径的缩小没有影响输出激光的功率性能。
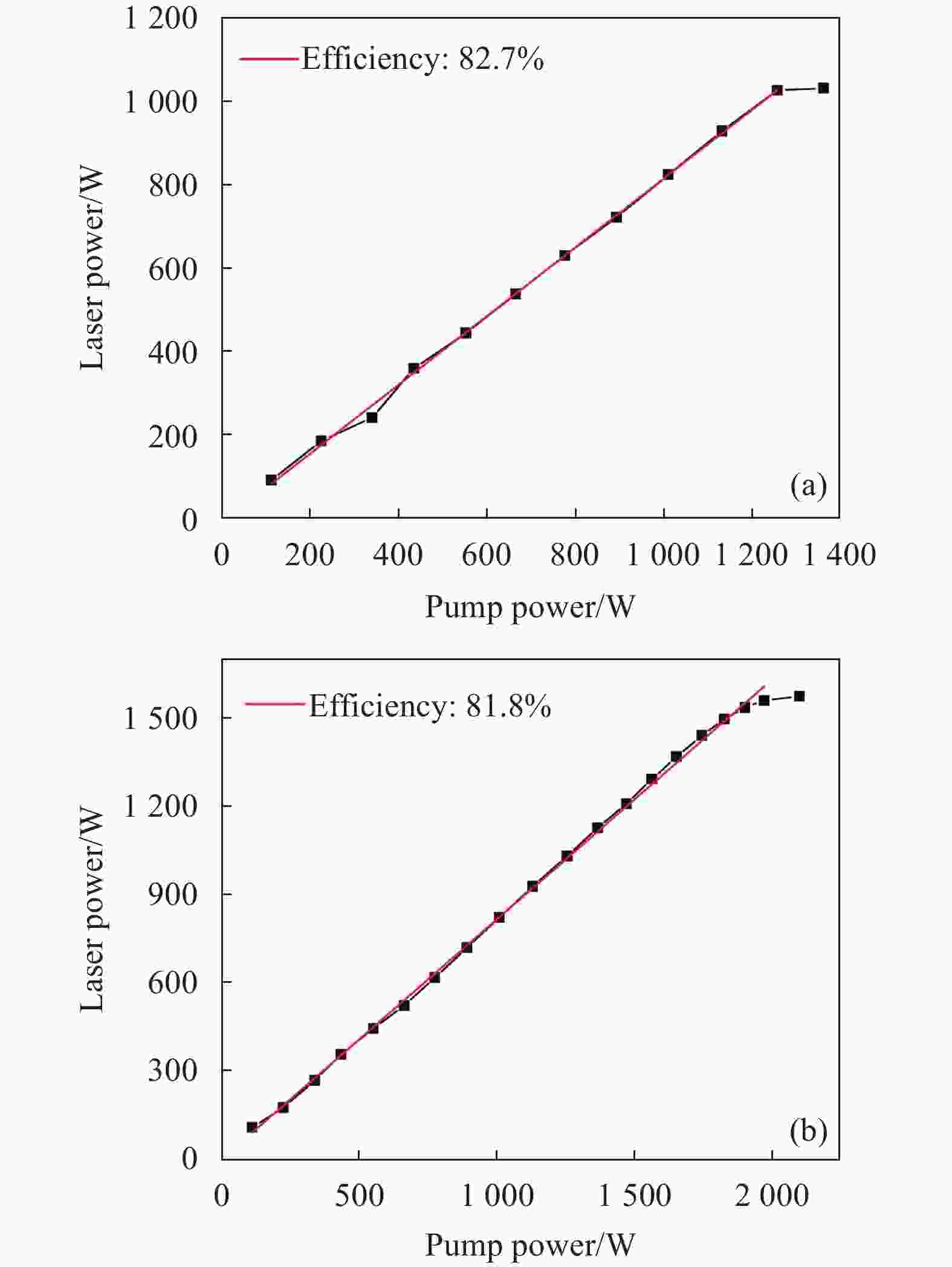
图 7 弯曲半径分别为(a) 6 cm和(b) 5 cm时输出激光功率随泵浦功率的变化结果
Figure 7. Output power versus pump power when the bending radius are (a) 6 cm and (b) 5 cm, respectively
为进一步强化对TMI现象的探测,继续利用高反镜取样输出激光衰减到实验室现有的CCD相机,对激光器输出的光斑特性进行在线监测,受限于CCD的响应速率(12 fps),在功率持续增长的过程中并未发现明显的模式跳变现象,但由于存在高阶模的耦合竞争,导致输出光斑的形态不再是标准的高斯光场,出现了一定程度的畸变,在1033 W和1567 W的功率量级下观测到的光斑分布如图8所示。实验过程中,通过对后向回光的实时监测发现,当TMI现象初步显现后,后向光谱还比较稳定。但当驱动电流进一步增加至形成较强的TMI现象时,后向时域和光谱都会开始出现抖动。这可能是因为前向功率发生振荡变化后,引起后向的瑞利散射也随之变化,导致测量到的后向光功率信号出现抖动。
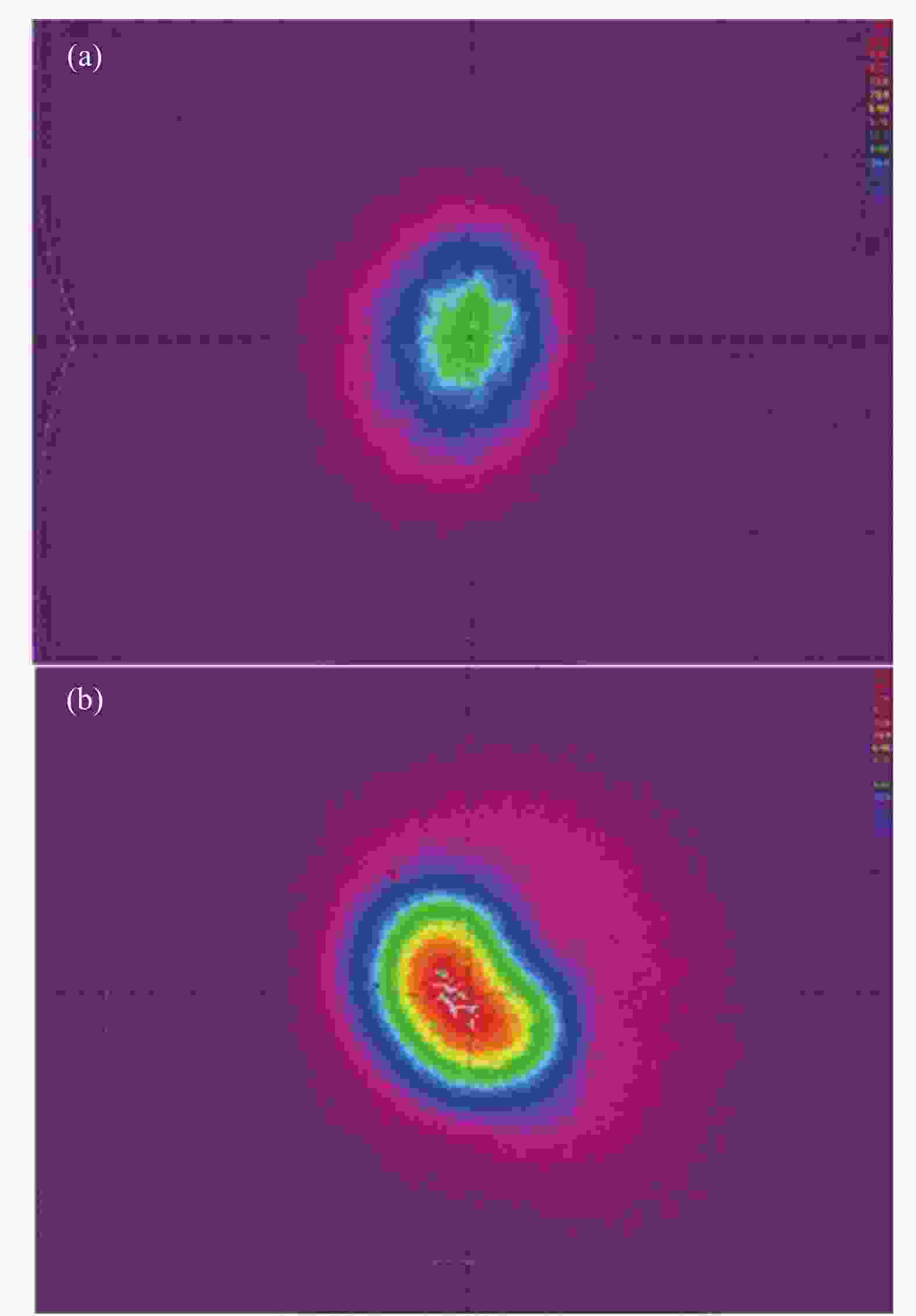
图 8 (a) 1033 W和(b) 1567 W功率量级下CCD采样的输出光斑
Figure 8. Output beam acquired by CCD at the power level of (a) 1033 W and (b) 1567 W
根据前文探测到的实验现象,不难发现,对比TMI发生前后光功率信号产生的频率噪声谱,首先会在1~10 kHz的范围内出现明显的噪声包络,然后随着泵浦功率的进一步增长会逐步过渡到2.5~3 kHz附近的噪声尖峰。对照非线性耦合系数的变化曲线,当LP01和LP11模之间的耦合频率分布在1~10 kHz的范围内,非线性耦合系数的强度值相对较大,其中最大的耦合频率发生在3 kHz附近,理论计算与实验结果的变化趋势相一致。而对于高功率光纤激光系统的TMI阈值范围评估,理论计算的数值结果跟实验系统的测试数据存在着些许偏差,误差来源的主要原因在于文中计算得到的各模式间非线性耦合系数是在大模场光纤未弯曲情况下的一种近似,弯曲限模之后可能会引发非线性耦合强度的变化,这种差异化的耦合强度对TMI的阈值评估带来了影响。除此之外,光纤激光系统参数的取值偏差也会对最后的计算结果造成一定的影响,这些问题我们将在接下来的研究工作中逐步去完善解决。当前理论仿真的计算结果虽不能代表严格意义上的TMI阈值,但是却可以直观对比说明弯曲限模对TMI的有效抑制,而且也能快速评估得到高功率光纤激光系统的阈值范围,为高功率光纤激光器的参数设计提供了简化的理论模型和参考依据。
综上,基于窄线宽高功率全光纤化的实验平台,针对两种不同的弯曲半径,从输出激光的多维度性能参数综合分析确认了TMI效应的发生。实验结果表明,缩小大模场面积增益光纤的弯曲半径,可以实现更佳的模式滤波效果,从而有效提高TMI现象的阈值。
-
随着大模场面积光纤的使用和激光器输出功率的不断提高,光纤激光器中的横模不稳定性已经成为限制其发展的最主要因素之一。文中利用TMI的半解析模型分析了大模场光纤25/400 μm中各高阶模的模式耦合系数,验证了次高阶模LP11的强耦合相互作用,因而导致大部分出现TMI现象的高功率光纤激光实验中,LP11模式会最先被观察到同时也最难被抑制掉,基于此考虑利用弯曲限模的方式来抑制TMI现象的发生。理论计算的结果表明,当大模场光纤的弯曲半径从6.5 cm缩小至4.5 cm,光纤激光系统的TMI阈值可以提升至4000 W量级。为了验证弯曲限模的实际效果,我们选取了中间的两个常规弯曲半径在同一窄线宽高功率光纤激光级联放大的MOPA平台进行实验探索,首先利用单频展宽的方式来抑制放大过程中的非线性作用,然后改变增益光纤的弯曲半径从6 cm缩小至5 cm,从而将激光器的TMI阈值从1000 W量级提升到1600 W量级,进一步的功率增长可能要考虑借助于其他更新颖的模式滤波技术。因为如果进一步缩小大模场光纤的弯曲半径会带来基模损耗的急剧增加,对整个激光系统的热积累带来严重的负荷,而且激光器的输出功率也会出现明显下滑。目前,有关TMI效应的研究主要集中在理论模型的建立和完善,而相关的实验探索有待进一步的拓展深入。
Influence of bending on transverse mode instability of large mode area fiber
-
摘要: 横模不稳定效应已经逐渐成为引起高功率光纤激光光束质量急剧恶化并限制其输出功率进一步提升的首要瓶颈问题。基于全光纤化正向泵浦的窄线宽高功率放大平台,对大模场光纤激光器中的横模不稳定效应进行了一系列的探索研究。根据耦合模方程的计算结果,所用大模场光纤25/400 μm中LP01、LP11模之间的非线性耦合强度最大,这也直接诱导了横模不稳定效应的发生。为了抑制LP11模在主放大级的产生和放大,通过弯曲限模这种可操作性强的模式滤波技术,将主放增益光纤的弯曲半径从6 cm缩小至5 cm的过程中,高功率光纤激光系统的横模不稳定阈值从1000 W量级提高到了1600 W量级,而且激光器的其他输出性能几乎没有受到影响。这为构建实际的窄线宽高功率全光纤化的激光系统提供了强有力的实验参照。Abstract: The effect of transverse mode instability has gradually become the primary problem that causes laser beam quality degradation and limits power scaling of high-power fiber lasers. This paper conducts a series of study on the transverse mode instability (TMI) in large mode area (LMA) fiber based on a co-pumped all-fiberized narrow linewidth high power amplification platform. According to the calculation results of the coupled mode equations, the nonlinear coupling strength between the LP01 and LP11 modes of the LMA fiber 25/400 μm is the largest, which directly induces the TMI. In order to suppress the generation and amplification of the LP11 mode at the main amplifier, the fiber coiling method was used as an operational mode filtering technique to achieve mode control. The threshold of TMI increased from 1000 W to 1600 W while reducing the bending radius of the main amplifier gain fiber from 6 cm to 5 cm, and the other output performance of the fiber laser was hardly affected. This provides a powerful experimental reference for us to build an actual narrow linewidth, high power, all-fiberized laser system.
-
Key words:
- fiber laser /
- transverse mode instability /
- bending mode /
- nonlinear coupling coefficient
-
表 1 光纤激光系统的参数设置
Table 1. Parameters of fiber laser system
Parameter Value Parameter Value ${n_c}$ 1.45 $b$ 300 μm $\kappa $ 1.4 W/(m·K) $\eta $ 3.5×10−5 K−1 ${h_q}$ 1000 W/(m2·K) $\rho C$ 1.67×106 J/(m3·K) ${\lambda _p}$ 976 nm ${\lambda _s}$ 1064 nm -
[1] Tünnermann A, Schreiber T, Röser F, et al. The renaissance and bright future of fibre lasers [J]. Journal of Physics B Atomic Molecular & Optical Physics, 2005, 38(9): S681. [2] Jauregui C, Limpert J, Tünnermann A. High-power fibre lasers [J]. Nature Photonics, 2013, 7(11): 861-867. doi: 10.1038/nphoton.2013.273 [3] Zervas M N, Codemard C A. High power fiber lasers: a review [J]. IEEE Journal of Selected Topics in Quantum Electronics, 2014, 20(5): 219-241. doi: 10.1109/JSTQE.2014.2321279 [4] Stutzki F, Jansen F, Otto H, et al. Designing advanced very-large-mode-area fibers for power scaling of fiber-laser systems [J]. Optica, 2014, 1(4): 233. doi: 10.1364/OPTICA.1.000233 [5] Smith A V, Smith J J. Mode instability in high power fiber amplifiers [J]. Optics Express, 2011, 19(11): 10180-92. doi: 10.1364/OE.19.010180 [6] Jauregui C, Eidam T, Otto H J, et al. Physical origin of mode instabilities in high-power fiber laser systems [J]. Optics Express, 2012, 20(12): 12912-12925. doi: 10.1364/OE.20.012912 [7] Eidam T, Hanf S, Seise E, et al. Femtosecond fiber CPA system emitting 830 W average output power [J]. Optics Letters, 2010, 35(2): 94-96. doi: 10.1364/OL.35.000094 [8] Hansen K R, Alkeskjold T T, Broeng J, et al. Theoretical analysis of mode instability in high-power fiber amplifiers [J]. Optics Express, 2013, 21(2): 1944-1971. doi: 10.1364/OE.21.001944 [9] Dong L. Stimulated thermal Rayleigh scattering in optical fibers [J]. Optics Express, 2013, 21(3): 2642-2656. doi: 10.1364/OE.21.002642 [10] Naderi S, Dajani I, Madden T, et al. Investigations of modal instabilities in fiber amplifiers through detailed numerical simulations [J]. Optics Express, 2013, 21(13): 16111-16129. doi: 10.1364/OE.21.016111 [11] Smith A V, Smith J J. Overview of a steady-periodic model of modal instability in fiber amplifiers [J]. IEEE Journal of Selected Topics in Quantum Electronics, 2014, 20(5): 472-483. doi: 10.1109/JSTQE.2013.2296372 [12] Tao R, Wang X, Zhou P. Comprehensive theoretical study of mode instability in high-power fiber lasers by employing a universal model and its implications [J]. IEEE Journal of Selected Topics in Quantum Electronics, 2018, 24(3): 1-19. [13] Chu Q, Tao R, Li C, et al. Experimental study of the influence of mode excitation on mode instability in high power fiber amplifier [J]. Scientific Reports, 2019, 9(1): 1-7. doi: 10.1038/s41598-018-37186-2 [14] Jauregui C, Stihler C, Tu Y, et al. Mitigation of transverse mode instability with travelling waves in high-power fiber amplifiers[C]//Fiber Lasers XVII: Technology and Systems. International Society for Optics and Photonics, 2020, 11260: 112601A. [15] Tao Rumao, Wang Xiaolin, Xiao Hu, et al. Theoretical study of the threshold power of mode instability in high-power fiber amplifiers [J]. Acta Optica Sinica, 2014, 34(1): 0114002. doi: 10.3788/AOS201434.0114002 [16] Stihler C, Jauregui C, Kholaif S E, et al. Intensity noise as a driver for transverse mode instability in fiber amplifiers [J]. PhotoniX, 2020, 1(1): 1-17. doi: 10.1186/s43074-020-00006-w [17] Marcuse D. Curvature loss formula for optical fibers [J]. JOSA, 1976, 66(3): 216-220. doi: 10.1364/JOSA.66.000216 [18] Tao R, Su R, Ma P, et al. Suppressing mode instabilities by optimizing the fiber coiling methods [J]. Laser Physics Letters, 2016, 14(2): 025101. [19] Eidam T, Wirth C, Jauregui C, et al. Experimental observations of the threshold-like onset of mode instabilities in high power fiber amplifiers [J]. Optics Express, 2011, 19(14): 13218-13224. doi: 10.1364/OE.19.013218 [20] Tao R, Ma P, Wang X, et al. Experimental study on mode instabilities in all-fiberized high-power fiber amplifiers [J]. Chinese Optics Letters, 2014, 12(s2): s20603. doi: s20603 -






 下载:
下载:



















































