-
射流是工程应用经常利用的一种流动现象,典型的如航空发动机的高温尾喷流。尾喷流是发动机排气系统在3~5 μm中波波段的重要辐射源,在90°探测方向(垂直于机身方向),尾喷流的辐射占排气系统整体辐射的90%以上。在飞机加力状态下,尾喷流辐射强度增加是排气系统红外辐射大幅提高的主要原因。因此,研究尾喷流在中波波段内的红外辐射特性具有重要的意义。
发动机尾喷流的辐射力主要由其温度的4次方,以及燃气内包含的CO2、H2O和CO等参与性介质的浓度决定。在实际应用中,尾喷流的雷诺数(Re)通常高达106或以上,湍流度很高,温度和组分浓度具有强烈的湍流脉动特性。目前,计算尾喷流红外辐射特性的主要方法是先利用雷诺平均方法计算出尾喷流流场的平均温度和平均组分浓度等分布,然后再计算其平均红外辐射强度[1-3],不考虑湍流引起的温度脉动和组分浓度脉动等对辐射的影响。目前,湍流对辐射的影响研究主要集中于火焰研究,而在湍流对尾喷流红外辐射影响研究方面,仅可查到Blunck等[4-5]的一些研究。Blunck等[4]利用采样频率高达11 300 Hz的高速红外摄像机,测量了Re=2.3×105~2.6×105的射流流场的红外辐射亮度分布,获取了红外辐射强度的湍流特性,比如脉动强度和概率密度等参数的分布规律,发现尾喷流的辐射强度脉动特性与火焰的辐射强度脉动特性类似。此外,Blunck等[5]还利用DES(Detached Eddy Simulation)方法对流场进行了计算,获得流场的平均温度和平均组分浓度,以及瞬时温度和瞬时组分浓度分布,并对比了基于平均参数和瞬时参数计算的红外辐射强度,发现湍流脉动对尾喷流的影响沿流向和径向逐渐增强。不过Blunck研究的射流区域较小,仅集中于喷管出口附近流向6D范围内,而且只针对辐射亮度进行分析,未提及积分辐射强度等在红外探测中常用于衡量目标红外辐射强度的变量。
为深入理解尾喷流的红外辐射特性,文中以高温燃气圆射流为对象,首先采用大涡模拟方法计算出流场的瞬时温度和瞬时组分浓度,以及平均温度和平均组分浓度等参数,然后在此基础上分别利用流场的瞬时参数和平均参数计算射流的红外辐射特性,最后对比了两种方法计算的光谱辐射强度、积分辐射强度和辐射亮度等,研究了湍流脉动对高温燃气圆射流红外辐射特性的影响。
-
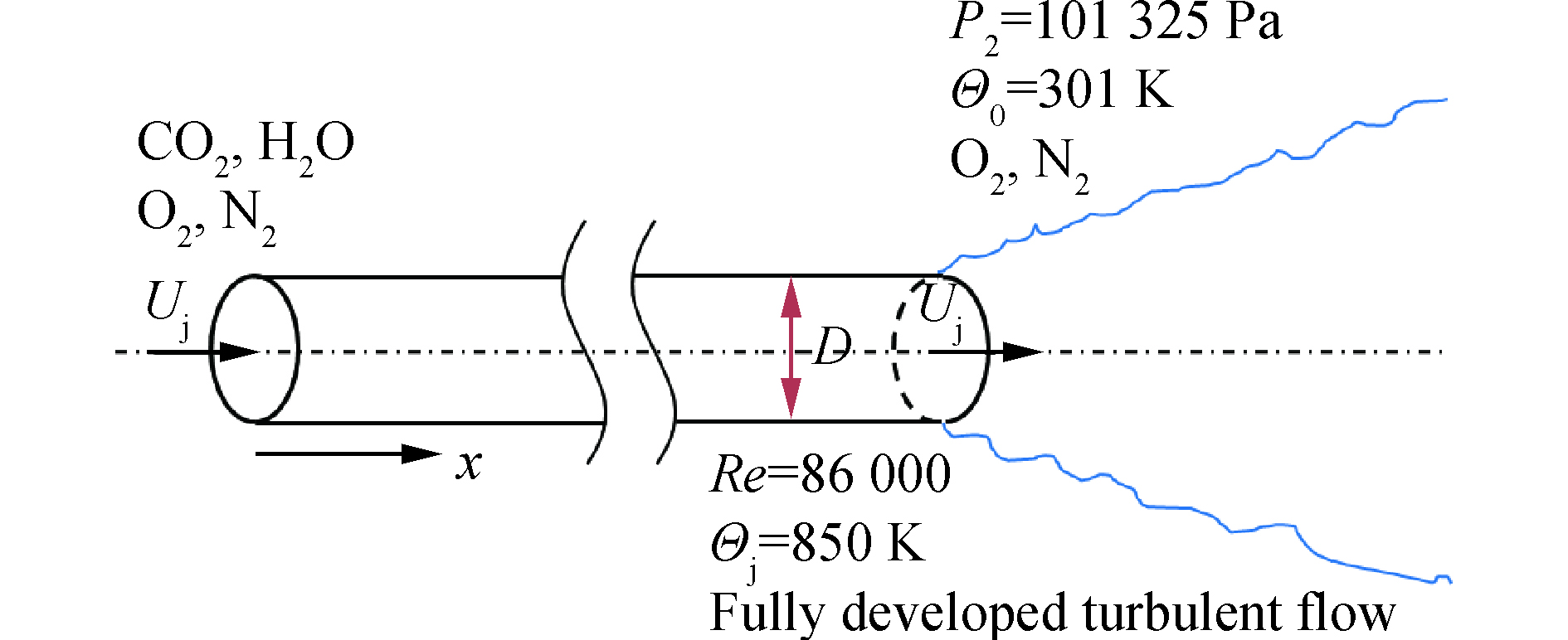
文中计算的物理模型为Re = 86 000(基于射流进口截面平均速度Uj和直径D)的圆管射流,如图1所示。圆管长度足够长,使流体在喷出管道前就达到充分发展状态,管内流体温度处处相等,射流进口截面平均温度Θj = 85 K。射流所处环境压力为
${P_0}$ =101 325 Pa,温度Θ0 = 301 K,环境温度与进口温度之比为0.35。射流进口气体为航空煤油完全燃烧且未生成CO的产物,其中辐射参与性介质为CO2和H2O,其质量浓度分别为0.048 9和0.02,剩余组分为O2和N2,其质量浓度分别为0.165 4和0.765 7。环境空气中仅考虑O2和N2,质量浓度分别为0.232和0.768,其余气体不计。 -
流场计算采用FLUENT软件中植入的LES方法。射流场的计算域为长31D,直径20D的圆柱区域,其中包含0.5D长的管道区域,以及30D长的射流发展区域,如图2所示。LES方法要求网格分辨率达到惯性子尺度的量级,但如何确定射流的惯性子尺度目前并没有实用的普适性标准可参考。参考文献[6-7]采用大涡模拟计算了Re数略大于文中计算工况的射流,计算结果与实验值吻合较好,说明其网格设置合理,因此文中参考文献[6-7]的网格分辨率对计算域进行网格划分。网格为六面体形状,总量约为720万,流向、径向和周向分布数量为514×140×100,网格尺寸沿流向和径向逐渐增大,沿周向均匀分布。图中红色框区域为射流主要发展区域,占据了85%的网格量,该区域内最小网格在管道出口截面处,其流向、径向和周向尺寸分别约为0.02D、0.002D和0.03D,最大网格在管道出口下游25D,半径6.5D处,其流向、径向和周向尺寸分别约为0.11D、0.08D和0.4D,射流主要发展区域内网格分辨率与参考文献[6-7]中算例的分辨率相当。
流体进口设置为速度进口,给定瞬时速度、瞬时静温和组分浓度分布,其中瞬时静温和组分浓度根据工况设置为常数,瞬时速度则来源于预先计算好的充分发展管道流动。射流场出口设置为压力出口,给定静压
${P_0}$ 和总温Θ0。管道壁面为无滑移、绝热壁面。流体设置为不可压理想气体。由于射流的Grd/Re2<<1,计算时不考虑重力和浮升力的影响,此处Grd为Grashof数,是评价流体粘性力和浮升力相对大小的无量纲数[8]。大涡模拟中亚格子模型采用WALE模型模拟[9],动量方程采用中心差分格式离散,能量方程和组分传输方程采用有界中心差分格式离散。时间推进格式采用二阶隐式。时间步长
$\Delta t$ 设置为0.018D/Uj,使流场中CFL数最大值在1.1左右。计算在270D/Uj时开始采样进行统计,统计时长为540 D/Uj。 -
为研究湍流脉动对射流红外辐射特性的影响,文中采用以下两种方法计算红外辐射强度:
(1)平均温度−辐射法
该方法根据流场的时间平均参数计算射流场的时间平均红外辐射特性。为方便叙述,下文中将“时间平均”简写为“平均”。
在不考虑散射情况下,参与性介质内辐射亮度传输方程为:
$$ \frac{{{\rm d}{L_\lambda }}}{{{\rm d}S}} = {\rm{ - }}{\alpha _\lambda }{L_\lambda }\left( S \right){\rm{ + }}{\alpha _\lambda }{L_{\lambda b}}\left( S \right) $$ (1) 式中:
${L_\lambda }$ 为平均光谱辐射亮度,W/(cm2·sr·µm);${L_{\lambda b}}$ 为平均黑体光谱辐射亮度;${\alpha _\lambda }$ 为平均光谱吸收率;S为穿透距离。根据普朗克定律,公式(1)中等号右边第二项可表达为:$$ {\alpha _\lambda }{L_{\lambda b}}{\rm{ = }}\frac{{{\alpha _\lambda }{c_1}}}{{\pi {\lambda ^5}}}\frac{1}{{\exp \left( {{{{c_2}} / {\left( {\lambda \varTheta } \right)}}} \right){\rm{ - }}1}} $$ (2) 式中:c1和c2为辐射常数;
$\lambda $ 为波长Θ为平均温度。在该方法中,公式(1)和(2)中的变量均根据参与性介质的平均组分浓度$Y$ 、平均压力$P$ 和平均温度Θ计算,因此,可直接计算出流场的平均红外辐射亮度、平均光谱辐射强度以及平均积分辐射强度。(2)瞬时温度−辐射法
该方法根据流场的瞬时参数计算射流场的红外辐射特性的平均值及脉动值。瞬时的辐射亮度传输方程可写为:
$$ \frac{{{\rm d}{{\tilde L}_\lambda }}}{{{\rm d}S}} = {\rm{ - }}{\alpha _\lambda }{\tilde L_\lambda }\left( S \right){\rm{ + }}{\tilde \alpha _\lambda }{\tilde L_{\lambda b}}\left( S \right) $$ (3) 其中,
$$ {\tilde \alpha _\lambda }{\tilde L_{\lambda b}}{\rm{ = }}\frac{{{{\tilde \alpha }_\lambda }{c_1}}}{{\pi {\lambda ^5}}}\frac{1}{{\exp \left( {{{{c_2}} / {\left( {\lambda {{\tilde \varTheta }} } \right)}}} \right){\rm{ - }}1}} $$ (4) 式中:上标“~”指代瞬时变量;
${\tilde L_\lambda }$ 为瞬时光谱辐射亮度;${\tilde L_{\lambda b}}$ 为瞬时黑体光谱辐射亮度;${\tilde \alpha _\lambda }$ 为瞬时光谱吸收率;$\tilde \varTheta $ 为瞬时温度。公式(3)和(4)中的变量均基于参与性介质的瞬时组分浓度$\tilde Y$ 、瞬时压力$\tilde P$ 和瞬时温度$\tilde \varTheta $ 等得到,由此,可计算出流场的瞬时红外辐射亮度、瞬时光谱辐射强度和瞬时积分辐射亮度等参数,在此基础上进行时均统计计算,可获得光谱辐射强度、积分辐射强度和辐射亮度的平均值及其脉动值。公式(5)和(6)以瞬时辐射强度$\tilde I$ 为例说明时均统计方法。$$ I = \frac{1}{T}\int_0^T {\tilde I{\rm d}t} $$ (5) $$ {I_{\rm rms}} = \sqrt {\frac{1}{T}\int_0^T {{{\left( {\tilde I - I} \right)}^2}{\rm d}t} } $$ (6) 式中:I为红外辐射强度的平均值;下标“rms”为其脉动均方根值;T为统计时长;t为时间。
-
文中计算的红外辐射为目标自身的辐射,不考虑大气吸收作用。红外辐射特性计算利用课题组自主研发的飞行器红外特性分析软件NUAA-IR,该软件可导入FLUENT计算的流场,然后采用反向蒙特卡洛法计算流场的红外辐射强度[10]。
为研究射流场不同区域处湍流脉动对射流红外辐射的影响,文中沿流向每隔2D长度取直径为Dir的圆柱区域作为红外计算域,如图3所示,其中Dir取值见表1。由于射流场的温度核心区和温度脉动较强区域在x/D<15范围内,红外计算域仅取到流向14D处。在每个计算域内,探测角的立体空间划分为320×240个像素,每个像素内的射线数为40条,每个计算域内网格划分数目见表1。在选取探测方向时,考虑到在垂直于流场轴线方向上(90°方向)观察到的射流湍流现象最明显,仅计算了该方向的红外辐射。
表 1 红外计算域设置
Table 1. Settings of the IR calculation domain
Name of calculation domains x/D Dir/D Mesh numbers Axial direction Tangential direction Radial direction IR_1 0-2 2.8 120 100 120 IR_2 2-4 4.1 90 100 100 IR_3 4-6 5.2 80 100 80 IR_4 6-8 6.2 60 100 80 IR_5 8-10 7.0 60 100 80 IR_6 10-12 7.6 40 100 100 IR_7 12-14 8.4 30 100 100 采用瞬时温度−辐射法需计算多组流场样本的红外辐射。文中流场采样频率为2 000 Hz,采样间隔时间为25
$\Delta t$ 。介质从射流进口运动到计算域末尾所需时长为300×25$\Delta t$ ,所以样本数量选为370,以保证样本包含整个流场信息。为考察样本数量对统计结果的影响,又额外采集了200个流场样本。图4为样本数量分别为370和570时,IR_5计算域的光谱−辐射强度分布,图中${I_\lambda }$ 和${I_{\lambda ,{\rm rms}}}$ 分别表示光谱辐射强度的平均值及其脉动均方根值,单位为W/(µm·sr)。由图可见,370个样本数量的统计结果与570个样本数量的统计结果几乎一致,因此文中样本长度定为370。 -
图5(a)、(b)和(c)分别为射流场对称面上瞬时温度、平均温度和脉动温度均方根分布,其中图5(b)包含射流进口附近局部放大图。图中
${\theta _{\rm rms}}$ 表示温度的脉动均方根值。由于文中仅针对射流区域的红外特征进行研究,不考虑固体壁面的辐射特性,所以图中仅显示了射流区域。由图5可看出,射流与环境冷流体接触的掺混区域沿流向逐渐增大,核心区逐渐缩小,并在x/D=4附近消失;掺混区内温度脉动较高,且沿着流向逐渐降低,脉动值较大的区域在x/D<15范围内。射流场的组分浓度分布与温度场十分接近,这里不再赘述。 -
图6为IR_1~IR_7计算域内流场的3~5 μm波段光谱辐射强度平均值
${I_\lambda }$ 的分布,图中带下标“$\varTheta $ ”的变量表示采用平均温度−辐射法计算,未带此下标则表示采用瞬时温度−辐射法计算,下文中表示方法相同。图6将IR_1~IR_7计算域的计算结果绘制在一张图中以便对比分析。计算结果显示介质仅在4.2~4.5 μm之间呈现较强辐射能力,这是由于计算时仅考虑了射流中参与性介质CO2和H2O的辐射,不计算固体壁面辐射。由图6(a)可看出,所有计算域的${I_{\lambda ,\varTheta }}$ 都低于${I_\lambda }$ ,说明未考虑湍流影响计算得到的红外辐射强度偏低。${I_\lambda }$ 与${I_{\lambda ,\varTheta }}$ 的整体分布趋势一致,二者在4.2~4.5 μm波段内的峰值在射流进口附近区域最大,随着计算域移向下游,峰值随之降低,这是由于高温燃气与外界冷流体不断掺混,导致红外辐射强度沿流向逐渐降低。图6(b)是各计算域内采用瞬时温度−辐射法计算的光谱辐射强度的脉动值分布,由图可知,脉动值${I_{\lambda ,{\rm rms}}}$ 呈现先上升后下降的趋势,并且在IR_3计算域内达到最大值,此处是${I_\lambda }$ 与${I_{\lambda ,\varTheta }}$ 相差较大的区域,对应了射流高温核心区尾缘区域。对比图5和图6(b)可知,从IR_1至IR_3,湍流脉动强度减弱,但由于掺混厚度快速增加,湍流脉动影响的区域增大,所以对应区域的${I_{\lambda ,{\rm rms}}}$ 逐渐升高;从IR_3至IR_7,虽然掺混厚度保持增长,但湍流脉动强度持续降低至0左右,对应区域${I_{\lambda ,{\rm rms}}}$ 逐渐降低。这说明湍流脉动对射流红外辐射的影响与湍流脉动大小和掺混区厚度均有关,在射流初始发展阶段,湍流脉动对红外辐射影响程度变大的原因主要在于掺混区厚度快速增长,而在高温核心区尾缘往后,湍流脉动对红外辐射影响程度降低的主要原因是湍流脉动强度减小。 -
对光谱辐射强度
${I_\lambda }$ 沿波长进行积分可获得积分辐射强度$I$ 。图7(a)显示了射流场在IR_1至IR_7计算域内3~5 μm波段的积分辐射强度平均值和脉动均方根值的分布情况,图中横坐标对应的是红外计算域流向坐标的中值。由图可看出,积分辐射强度的分布与光谱辐射强度一致,即沿流向的变化与光谱辐射强度一致,沿流向逐渐下降,而且采用瞬时温度−辐射法计算的积分辐射强度较高;红外辐射脉动值先上升后下降,并在IR_3计算域内达到最大值。公式(7)定义了采用瞬时温度−辐射法计算的平均辐射强度相对于采用平均温度−辐射法计算的平均辐射强度之间的相对差值比:
图 7 3~5 μm波段的积分辐射强度平均值和脉动均方根值分布
Figure 7. Mean and fluctuation root mean square of integrated radiation intensity between 3-5 μm band
$$ {\delta _I} = \frac{{I - {I_\varTheta }}}{{{I_\varTheta }}} $$ (7) 图7(b)为IR_1至IR_7计算域内采用两种方法计算的红外辐射强度之间的相对差值比
${\delta _I}$ 、绝对值差值$I - {I_\varTheta }$ 以及红外辐射脉动强度${{{I_{\rm{rms}}}} / I}$ 的分布情况。在射流进口附近区域,射流刚开始与环境流体掺混,掺混区较薄,但是湍流脉动大,因此$I - {I_\varTheta }$ 在IR_1和IR_2计算域内并不小,说明湍流脉动对红外辐射的影响受湍流脉动大小和掺混区厚度的共同影响。另外,IR_1和IR_2计算域内的${\delta _I}$ 较小,这主要是因为射流进口区域附近仍处于高温核心区,平均积分辐射强度较高。随着流动的发展,红外辐射强度下降,掺混区面积增大,$I - {I_\varTheta }$ 和${\delta _I}$ 都呈现先上升后下降的趋势,其中$I - {I_\varTheta }$ 在IR_3计算域内达到最大值0.56 W/sr,而${\delta _I}$ 则在略靠下游的IR_4计算域内达到最大值73.5%。红外辐射脉动强度${{{I_{\rm{rms}}}} / I}$ 沿流向也是先上升后缓慢下降,并在IR_5计算域内达到最大值17.5%。结合图7(a)可看出,相对差值比${\delta _I}$ 和脉动强度${{{I_{\rm{rms}}}} / I}$ 的峰值位置较绝对值差值$I - {I_\varTheta }$ 的峰值位置后移的原因主要在于积分红外辐射强度平均值的降低,而受湍流脉动的影响相对较小。因此,仍可以判定湍流脉动对射流红外辐射特性影响最大的区域位于IR_3区域,即射流高温核心区尾缘附近。由上述分析可知,采用瞬时温度-辐射法计算的平均积分辐射强度
$I$ 比采用平均温度-辐射法计算的平均积分辐射强度${I_\varTheta }$ 大,但图7中的差值只体现了局部辐射强度的差异,而工程应用中更关心视场空间的辐射强度总和,即各红外计算域的积分辐射强度之和:$$ {I_{\rm{sum}}} = \sum\limits_{m = 1}^M {{I_m}} ,\;\;m = 1,2,3... $$ (8) 式中:下标“sum”表示求和,M表示计算域总数。由公式(8)可得
${I_{\rm{sum}}} = 11.35\; {\rm {W/sr}}$ ,${I_{\varTheta ,\;{\rm sum}}} = 9.18\;{{\rm W/sr}}$ ,二者之间的相对差值比达到了23.6%,这说明湍流脉动对红外辐射强度的影响不可忽视。在红外辐射探测中,探测器接收的是当前时刻目标的红外辐射强度,所以采用瞬时温度−辐射法计算的红外辐射强度更符合实际应用,而且计入温度和组分浓度脉动对红外辐射的影响还可提高目标的安全阈值。 -
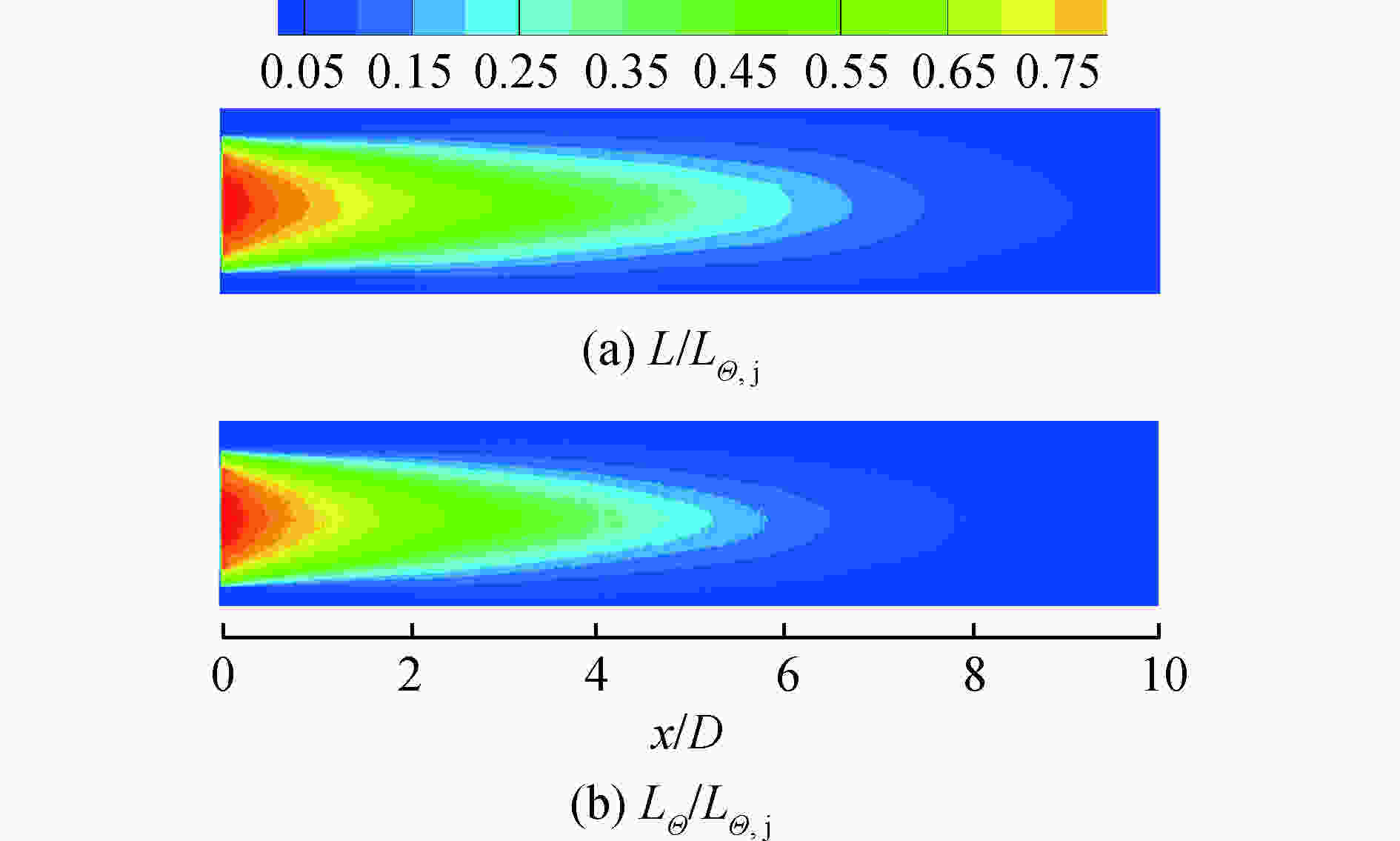
红外辐射亮度(单位W/(sr·cm2))分布可以直观显示出目标的红外特征。图8(a)和8(b)分别是采用瞬时温度−辐射法和采用平均温度−辐射法计算的探测视场内射流场的红外辐射亮度平均值分布,图中L表示辐射亮度,带下标“j”表示位于射流进口截面。由图可知,采用瞬时温度−辐射法计算的平均辐射亮度比平均温度−辐射法计算的平均辐射亮度更高,幅度亮度能标记出的区域更大,再次说明不考虑湍流脉动影响时计算的红外辐射强度偏低。对比图5(b)可知,平均辐射亮度和平均温度的分布沿流向都呈现降低趋势,但是辐射亮度没有出现与温度分布类似的核心区,这是因为红外辐射计算是从探测器视场出发,计算的是每一个视场线穿过的所有区域内的气体辐射。对于射流来说,从探测器视场出发,首先看见的是温度核心区外围的低温掺混区,随着射流向下游发展,核心区径向范围被压缩,掺混区变厚,射流中卷入的外界冷气增多,所以辐射亮度沿流向持续下降,没有出现核心区。
图9为红外辐射亮度平均值在流向x/D=1、3、5、7、9处的径向分布,该图反映了采用瞬时温度−辐射法和采用平均温度−辐射法计算的红外辐射亮度平均值之间的差值分布规律。由图可看出二者之间的差值最大的区域在射流高温核心区尾缘附近(x/D=5),而且在同一流向位置,二者之间的差值沿着径向逐渐降低。
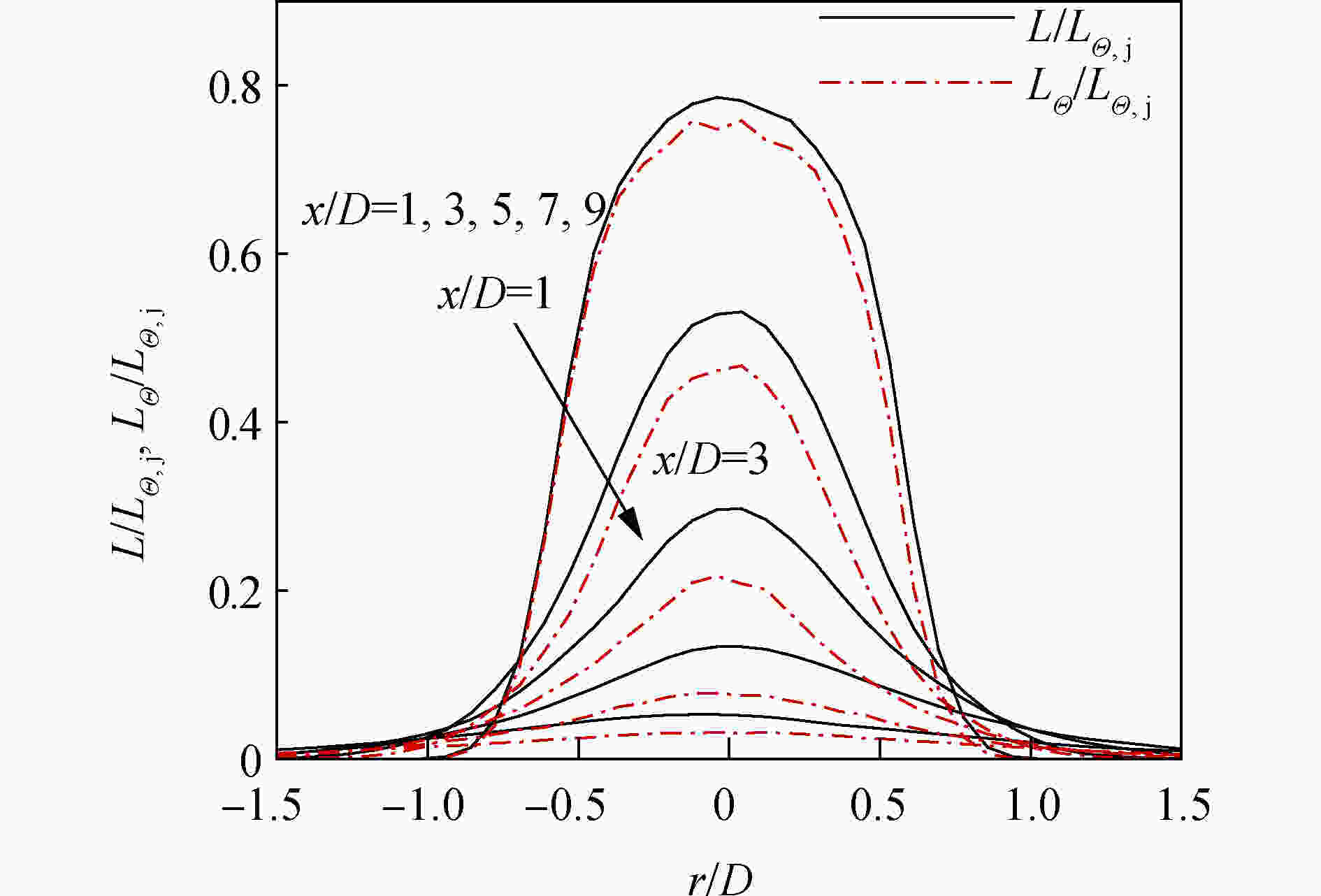
图 9 不同流向位置处辐射亮度平均值的径向分布
Figure 9. Radial profiles of radiation brightness mean at different axial locations
图10为采用瞬时温度−辐射法计算的射流场红外辐射亮度脉动均方根值分布。图中显示,辐射亮度脉动值的分布与温度脉动分布(图5(c))类似,但变化趋势不同。温度脉动在射流进口附近最大,而此处掺混区最薄,然后随着掺混区沿流向增厚,温度脉动逐渐降低。辐射亮度的脉动则呈现先增大后降低的趋势,并在约x/D=2处达到峰值。辐射亮度脉动值在峰值位置之前增大的原因主要是掺混区变厚,而在该位置之后,虽然掺混区厚度仍然在增大,但是湍流脉动强度下降,所以辐射亮度脉动值随之降低,这再次说明了湍流脉动对射流场红外辐射的影响程度由湍流脉动强度以及掺混区厚度的综合影响决定。
-
对高温燃气圆射流开展了大涡模拟计算,在此基础上分别采用瞬时温度−辐射法和平均温度−辐射法计算了射流场的光谱辐射强度、积分辐射强度和辐射亮度分布,分析对比两种方法的计算结果,获得了以下结论:
(1)采用瞬时温度−辐射法计算的平均光谱辐射强度、平均积分辐射强度和平均辐射亮度均高于采用平均温度法计算的结果。
(2)两种方法的计算结果之间的差值以及红外辐射的脉动幅值与湍流脉动大小和掺混区厚度均有关,湍流脉动越大,掺混区越厚,二者之间的差值越大,红外辐射强度的脉动幅值也越大,射流高温核心区尾缘附近是红外辐射脉动最强的区域。
(3)采用瞬时温度−辐射法计算的平均辐射亮度标记的目标范围比采用平均温度−辐射法的计算结果大,但两种方法计算的平均红外辐射亮度之间的差值沿着径向逐渐降低。
(4)对于Re=86 000,环境温度与进口温度之比为0.35 K的高温燃气圆射流,在90°探测方向上,采用瞬时温度−辐射法计算的总的积分辐射强度平均值比采用平均温度−辐射法计算的结果高23.6%左右。
Influence of turbulent fluctuations on the infrared radiation characteristics of round jet flow
-
摘要: 为研究湍流脉动对高温燃气圆射流红外辐射强度的影响,利用大涡模拟方法计算了高温圆射流流场的温度和组分浓度等的瞬时值和平均值,在此基础上分别采用平均温度−辐射法和瞬时温度−辐射法计算了射流场的红外辐射特性。计算结果表明:瞬时温度−辐射法计算的平均光谱辐射强度、平均积分辐射强度和平均辐射亮度均高于平均温度−辐射法计算的结果;湍流脉动越大,掺混区越厚,两种方法的计算结果之间的差值以及射流场红外辐射的脉动幅值均越大,其中射流高温核心区尾缘附近是受湍流影响最强的区域;两种方法计算的平均红外辐射亮度之间的差值沿着径向逐渐降低。对于Re=86 000,环境温度与进口温度之比为0.35的圆射流,在90°探测方向上,瞬时温度−辐射法计算的总的平均积分辐射强度比平均温度−辐射法的计算结果高23.6%左右。Abstract: To investigate the influence of turbulent fluctuation on the infrared radiation (IR) characteristics of high-temperature round gas jet flow, the instantaneous and time-averaged values of temperature and species concentration of a high temperature round jet flow was calculated using the Large Eddy Simulation, and then the IR characteristics of the jet flow was calculated by two methods: one was based on mean temperature and another was on instantaneous temperature. The results show that the time-averaged values of the spectral IR intensity, the integral IR intensity and the IR brightness calculated by the second method are higher than that calculated by the first method. Both the differences between the results of the two methods and the IR fluctuation increase with the turbulent fluctuation and mixing layer thickness increasing, and the area that is affected the strongest by the turbulent fluctuations is the vicinity of the trailing of the high-temperature core zone in the jet flow. The difference between the IR brightness calculated by the two methods gradually decrease along the radial direction. For the round jet flow at Re=86 000 and the ratio of the temperature of surrounded air and the jet inlet temperature is 0.35, the integral IR intensity at the 90° detection direction calculated by the second method is higher than that calculated by the first method by 23.6%.
-
表 1 红外计算域设置
Table 1. Settings of the IR calculation domain
Name of calculation domains x/D Dir/D Mesh numbers Axial direction Tangential direction Radial direction IR_1 0-2 2.8 120 100 120 IR_2 2-4 4.1 90 100 100 IR_3 4-6 5.2 80 100 80 IR_4 6-8 6.2 60 100 80 IR_5 8-10 7.0 60 100 80 IR_6 10-12 7.6 40 100 100 IR_7 12-14 8.4 30 100 100 -
[1] 王丁, 吉洪湖. 波瓣混合器排气系统红外特性的模型实验和数值分析[J]. 红外与激光工程, 2017, 46(1): 0104003. doi: 10.3788/IRLA201746.0104003 Wang Ding, Ji Honghu. Model experiment and numerical analysis on infrared character of lobed mixer exhaust system [J]. Infrared and Laser Engineering, 2017, 46(1): 0104003. (in Chinese) doi: 10.3788/IRLA201746.0104003 [2] 王丁, 吉洪湖, 卢浩浩. 波瓣混合器对双 S 形二元排气系统红外特性的影响[J]. 红外与激光工程, 2017, 46(2): 0204004. doi: 10.3788/IRLA201746.0204004 Wang Ding, Ji Honghu, Lu Haohao. Influence of Lobed mixer on infrared character of serpentine 2-D exhaust system [J]. Infrared and Laser Engineering, 2017, 46(2): 0204004. (in Chinese) doi: 10.3788/IRLA201746.0204004 [3] 王丁, 吉洪湖, 刘常春, 等. 截面变化类型对双S形二元排气系统性能的影响[J]. 推进技术, 2017, 38(1): 47-53. Wang Ding, Ji Honghu, Liu Changchun, et al. Effects of transection transformation form on performance of serpentine 2-D exhaust system [J]. Journal of Propulsion Technology, 2017, 38(1): 47-53. (in Chinese) [4] Blunck David L, Harvazinski Matthew E, Merkle Charles L, et al. Influence of turbulent fluctuations on the radiation intensity emitted from exhaust plumes [J]. Journal of Thermophysics and Heat Transfer, 2012, 26(4): 581-589. doi: 10.2514/1.T3802 [5] Blunck David L, Harvazinski Matthew E, Rankin Brent, et al. Turbulent radiation statistics of exhaust plumes exiting from a subsonic axisymmetric Nozzle [J]. Journal of Thermophysics and Heat Transfer, 2012, 26(2): 286-293. doi: 10.2514/1.T3621 [6] Kim Jungwoo, Choi Haecheon. Large eddy simulation of a circular jet: effect of inflow conditions on the near field [J]. Journal of Fluid Mechanics, 2009, 620: 383-411. doi: 10.1017/S0022112008004722 [7] Salkhordeh Sasan. Large eddy simulations of isothermal and non-isothermal turbulent flows for high temperature gas cooled reactors[D]. Pittsburgh: University of Pittsburgh, 2016. [8] Mi J, Nobes D S, Nathan G J. Influence of jet exit conditions on the passive scalar field of an axisymmetric free jet [J]. Journal of Fluid Mechanics, 2011, 432: 91-125. [9] Nicoud Franck, Ducros Frédéric. Subgrid-scale stress modelling based on the square of the velocity gradient tensor [J]. Flow Turbulence and Combustion, 1999, 62(3): 183-200. doi: 10.1023/A:1009995426001 [10] 黄伟, 吉洪湖, 斯仁, 等. 涡扇发动机排气系统红外特征[J]. 推进技术, 2010, 31(6): 745-772. Huang Wei, Ji Honghu, Si Ren, et al. Infrared characteristics calculating of turbofan engine exhaust system [J]. Journal of Propulsion Technology, 2010, 31(6): 745-772. (in Chinese) -







 下载:
下载: