三维重建相关技术在逆向工程、医疗、娱乐等领域的应用越来越多，其可以有效的优化生产过程，全面提升产品品质。随着科学技术的不断发展，高效精确的三维重建方法研究具有愈来愈重要的实际意义^[1-2]。

目前，已有的三维重建方法可以分为两种，一种是接触式测量，一种是非接触式测量。接触式测量方法的测量精度高，但测量效率较低，且三坐标测量机使用维护成本高，难以实现快速三维重建。非接触式测量具有非接触、效率高、无损伤等优点，其中尤属主动式结构光测量技术获得了更广泛的应用。根据相机数目不同可以分为多目结构光系统和单目结构光系统。多目结构光系统^[3]需要通过立体匹配得到待测物体视差图和深度图，但是立体匹配具有复杂的计算过程，计算量大，效率低下，且测量精度难以保证；单目结构光系统^[4]主要通过相机和投影仪的标定计算图像坐标系和空间坐标系之间的位置关系，从而重建物体的表面三维形貌，其方便、高效和测量精度高等特点吸引了诸多学者进行研究。主动结构光测量技术基于辅助光源照射进行三维测量，主要有干涉法、三角法和相位测量法等，其中干涉法^[5]具有较高的精度，但其视场范围小，对环境的要求高，因此大视场三维重建中应用较少；三角测量法根据物像系统之间的几何关系建立空间坐标系和图像坐标系之间的数学表达式，主要有光切法和激光三角法等。光切法^[6]适用性广、可控性强，但是光切法的光纹中心线提取误差较大，难以重建出高精度的三维形貌；激光三角法^[7]操作简单，测量精度较高，可选择线或面激光调整测量效率，但是该方法的测量精度易受环境光、待测表面等因素影响。相位测量法^[8]主要利用多步移相法对物体表面进行相位包裹，结合相位展开算法得到物体表面形貌。该方法速度快、精度高，是目前最热门的结构光三维重建研究方向，其中影响物体表面形貌求解效率和精度的关键是相位展开算法。传统的相位展开分为一维相位展开、二维相位展开和非连续性相位展开^[9-10]，一维和二维相位展开虽然求解效率高，但如果存在相位断层位置会极易引起误差传递，非连续性相位展开方法可以较好的避免这一问题，但是算法求解效率有待提高。

为解决非连续性相位展开算法效率低的问题，使其更高精度高效的应用于单目结构光测量系统，文中提出一种基于多鸽巢自适应排序的快速相位展开算法。首先构建像素组，并计算每个像素组的不可信值，依次放入从小到大的鸽巢中；而后判断误差传递是否满足要求，若不满足则在不可信值域区间重新构建鸽巢直到满足要求，保证相位展开的求解精度；接着从最小不可信值的鸽巢依次对像素组相位展开，得到相位主值；最终结合工业相机和投影仪的标定参数求解得到物体表面点云数据，极大地提升了单目结构光测量系统的计算效率和精度。

在结构光三维重建中，对待测物体的包裹相位进行相位展开会直接影响点云的求解精度^[11]。传统的相位展开算法是逐行列相位展开，如果上一点相位展开出错，将会引起误差传递，严重时会导致整个图形的相位展开错误。针对此问题，Miguel提出了一种非连续可靠性排序的相位展开算法^[12]，这种算法降低了误差传递，具有很好的相位展开效果, 其思路见下文。

该算法遵循高可信值像素先处理、低可信值像素后处理的原则来抑制误差的传播。决定该算法精度和效率的两个重要因素是：

（1）可信值函数的选择；

（2）相位展开路径的设计。

该算法选择的可信值函数为像素的二阶差分。一个像素周围应该有8个像素点环绕，如图1所示，假设该像素为$(i,j)$，则其他像素点分别为$(i - 1,j - 1)$、$(i,j - 1)$、$(i + 1,j - 1)$、$(i - 1,j)$、$(i + 1,j)$、$(i - 1,j + 1)$、$(i,j + 1)$和$(i + 1,j + 1)$。

图  1  像素二阶差分示意图

Figure 1.  Schematic diagram of pixel second-order difference

像素$(i,j)$的二阶差分$D(i,j)$由下式计算：

令$W[]$为相位包裹运算，其中：

像素可信值函数由下式定义：

式中：二阶差分值D越小，可信值R越大，像素越可靠。由于每次相位展开是在相邻两个像素之间进行，所以将相邻像素的可信值相加得到像素组的可信值。非连续性路径的可靠性排序算法的求解过程如下：

（1）计算图像的每个像素的可信值，分别按行列构建相邻像素组，计算像素组的可信值；

（2）按可信值大小排序像素组，引入求解组合概念，若两像素在一个求解组合中则转至（3）求解，若俩像素分属两个求解组合则转到（4）；

（3）对最大可信值像素组相位展开，并令该像素组为求解组合一；对第二大可信值像素组相位展开，若与求解组合一未相邻，则令该组合为求解组合二；然后根据可信值大小顺序，依次对两个求解组合中的像素组相位展开；

（4）若某个像素组在不同的求解组合中，从该像素组可信值大的一方进行相位展开，并将两个求解组合并；

（5）按照可信值大小排序对该合并求解组合进行求解，最后求解得到完整的展开相位图。

由上述算法可知，非连续路径可靠性排序的相位展开算法鲁棒性很高，对存在跳跃和噪点的相位具有很好的相位展开效果，但是在可信值排序过程中，仍可能存在可信值未严格按照从大到小顺序相位展开的情况，且每次相位展开前都要进行一次排序比较，算法的效率被极大限制。为此，文中提出一种基于多鸽巢自适应排序的快速相位展开算法，不但可以提升算法的计算效率，更可以保证相位求解的精度。

原始鸽巢排序算法是一种引入辅助数组的排序方式，将排序序列中待排序的数组索引值放入辅助数组中，但是原始鸽巢排序算法只引入一个辅助数组，极大地限制了算法的计算效率。文中提出的算法思路是在相位展开路径规划过程中引入多鸽巢辅助排序，将可信值排序分成两个阶段，分别是预排序和正排序。在预排序阶段自适应创建多鸽巢分组存储所有像素组的可靠性值，减少后期的正排序过程冗杂度。

由上分析可知，像素二阶差分的值域为$[0,4\pi ]$，而可信值函数的值域为$[1/4\pi , + \infty ]$。为了进一步减少计算量，直接定义像素$(i,j)$的不可信函数为：

可知${R_p}$的值域为$[0,16{\pi ^2}]$，则像素组的不可信值域为$[0,32{\pi ^2}]$。

首先，将像素组的不可信值值域等分成30个区间，根据不同的可信值区间构建30个等容鸽巢，计算所有像素组的不可信值，对其排序并对号入座放入对应鸽巢中。判断鸽巢的误差传递是否满足要求，即所有鸽巢的前30%是否可以包含95%的像素组，若不满足要求，则增加一个鸽巢并将像素组重新放置至对应鸽巢中，直到满足误差传递要求；若误差传递满足要求，就从第一个鸽巢开始相位展开，解完该鸽巢中的所有像素组相位，再对下一个鸽巢进行相位展开，直到全部解完为止。该算法的算法步骤如图2所示。

图  2  算法流程图

Figure 2.  Algorithm flowchart

根据算法，假设建立的像素差分计算模型与计算得到的像素不可信值如图3所示。将$[0,32{\pi ^2}]$的不可信值值域划分成30个鸽巢，然后分析所有像素组的不可信值和鸽巢的对应关系是否满足误差传递要求，前10个鸽巢的不可信值范围为$[0,105.2]$，从图3(b)可以看到只有i和j像素组不可信值超过105.2，满足条件的像素组占比95.83%，大于95%的误差要求，最终得到如图4所示的多鸽巢自适应排序结果。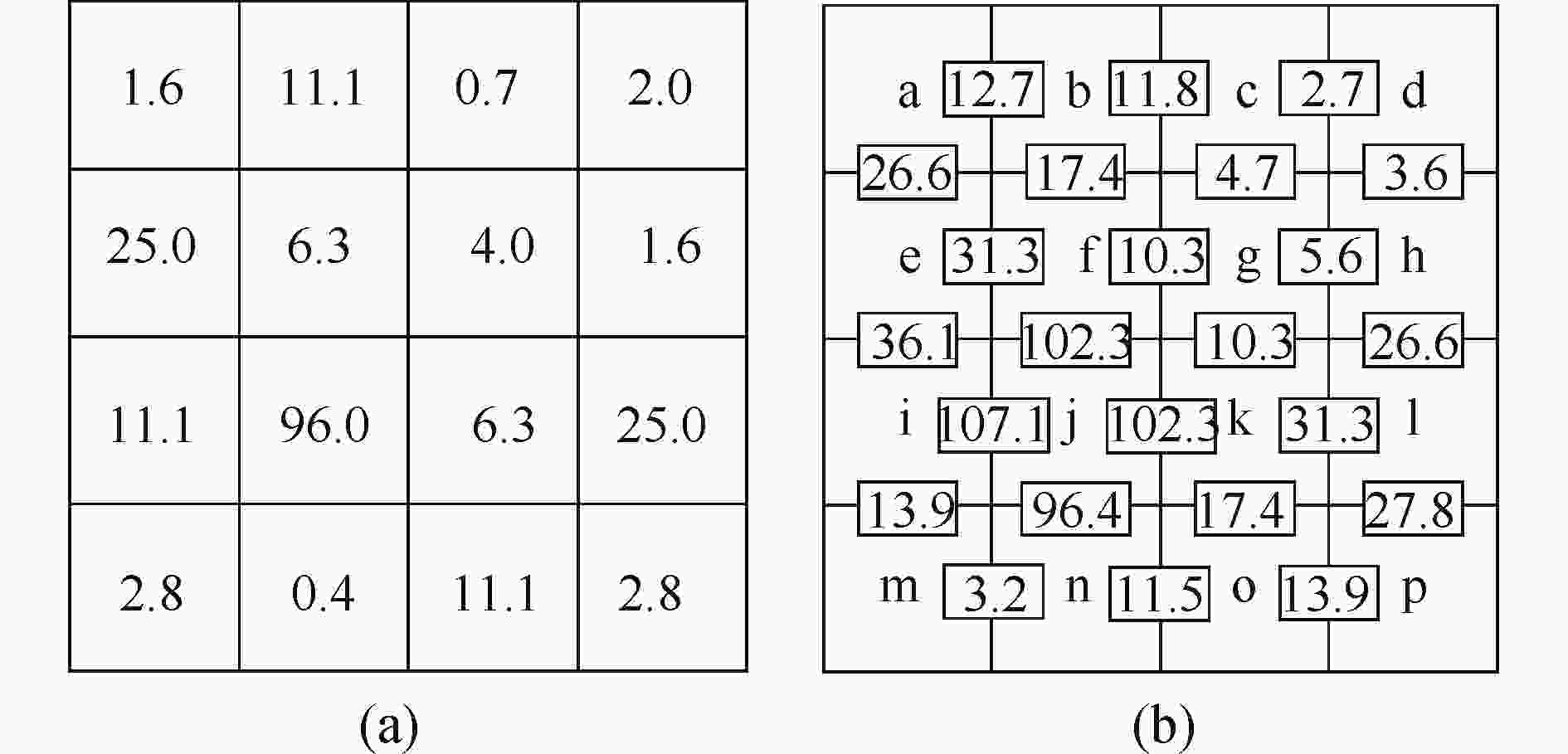

图  3  像素不可信值示意图。 (a)像素不可信值；(b)像素组不可信值

Figure 3.  Schematic diagram of pixel non-confidence value. (a) Pixel non-confidence values； (b) Pixel group non-confidence values

图  4  多鸽巢自适应排序结果

Figure 4.  Results of multiple pigeonholes adaptive sorting

由排序结果，可得基于多鸽巢自适应解相位方法对图像的解相过程如图5所示。由图4可知第一个鸽巢中含有7对像素组，在图5中可以对应找到分别为c和d，c和g，d和h，g和h，g和f，g和k以及m和n，首先对这些像素组进行相位展开求解，如图5(a)所示；第二个鸽巢中也包括7对像素组，分别为a和b，b和c，b和f，i和m，n和o，k和o以及o和p，接着对这些像素组进行相位展开求解，如图5(b)所示；以此类推，直到解开所有鸽巢中所包含的像素组，即可得到完整的相位展开图，如图5(d)所示。

图  5  相位展开求解过程

Figure 5.  Phase-unwrapping process

为验证算法有效性，文中对人脸模型进行解相位及三维重建实验，搭建的单目结构光测量系统如图6所示。

图  6  单目结构光测量系统

Figure 6.  Single-shot structured light system

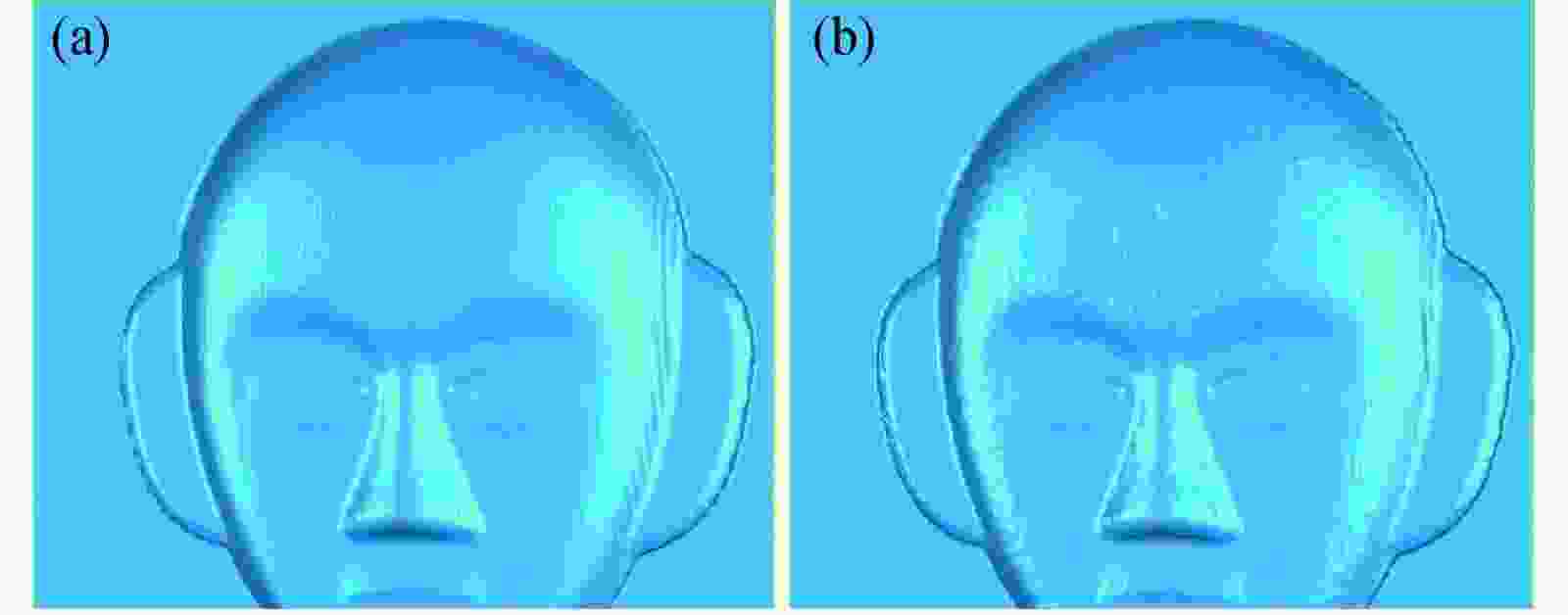
实验采用四步相移法进行光栅投射，对待测物体投影频率为135的正弦光栅得到如图7所示，四条光栅的相位值分别为$\pi /2$、$\pi $、$3\pi /2$和$2\pi $。

图  7  人脸四步移相光栅投影

Figure 7.  Four-step phase-shifted grating projection on face

根据文中提出的基于多鸽巢自适应排序的快速相位展开算法对待测物体的包裹相位进行相位展开计算，如图8所示，图8(a)为相位展开结果，图8(b)为相位展开后的相位高度图。

图  8  改进相位展开算法 。(a)人脸相位展开；(b)相位高度图

Figure 8.  Improved phas-unwrapping algorithm. (a) Phase unwrapping of face； (b) Phase height

利用非连续路径可靠性排序相位展开算法对待测物体包裹相位进行相位展开计算，如图9所示。图9(a)为相位展开结果，图9(b)为相位展开后的相位高度图。

图  9  原始相位展开算法。 (a)人脸相位展开；(b)相位高度

Figure 9.  Original phas-unwrapping algorithm. (a) Phase unwrapping of face；(b) Phase height

两种相位展开方法的应用场景和计算时间如表1所示，其中方法一为非连续路径可靠性排序的相位展开算法，方法二为基于多鸽巢自适应排序的快速相位展开算法。通过对1 024×768 pixels的包裹相位图像进行相位展开，原始算法用时3.44 s，而改进算法用时2.12 s，相比较提升了38.37%的计算效率。

根据单目结构光系统的相机及投影仪标定数据可以得到像素和实际空间坐标系之间的转换关系，从而计算得到利用文中相位展开算法求解后的人脸点云数据，该点云数据具有699 200个点。图10(a)、(b)分别为人脸点云的正视图、侧视图。

图  10  人脸点云。 (a)正视图；(b)侧视图

Figure 10.  Points cloud of face. (a) Front view；(b) Side view

该人脸模型的实际长度为260 mm，实际宽度为230 mm，实际高度为25 mm。通过对点云的正视图和侧视图的测量，可以看出利用文中相位展开算法得到的点云数据与实际的测量尺寸相符。

为进一步比较两种相位展开算法的求解精度，分别对这两种方法得到的点云数据进行三维重建，得到如图11所示的曲面，可以看出通过文中的相位展开方法计算得到的曲面平整度相较于原相位展开方法有显著提升。

图  11  点云曲面重建结果。 (a) 文中相位展开算法； (b) 原始相位展开方法

Figure 11.  Result of points cloud surface reconstruction. (a) Phase-unwrapping algorithm proposed in this paper ；(b) Original phase-unwrapping method

最后对整体叶盘面型投影测量实验，如图12~13所示。可以看出文中提出的相位展开方法在有相位阶跃的图像中依然有效应用。

图  12  叶盘四步移相光栅投影

Figure 12.  Four-step phase-shifted grating projection on blisk

图  13  改进相位展开算法。 (a)叶盘相位展开； (b)相位高度

Figure 13.  Improved phas-unwrapping algorithm. (a) Phase unwrapping of blisk；(b) Phase height

文中提出了基于多鸽巢自适应排序的快速相位展开方法，此方法引入多鸽巢排序的概念，通过多个鸽巢将每个像素组的不可信值进行分组排序，极大地优化了相位展开路径，相比于原算法提升了38.37%的计算效率；同时该算法在相位展开过程中自适应判断误差传递是否满足要求进一步保证了相位展开精度，从而有效提升点云求解精度。实验结果显示文中提出的算法较好地提升了单目结构光测量系统的测量精度和效率。