-
战术与战略导弹是现代战争中的“杀手锏”武器之一，是各国国防发展的利器。为应对导弹对国家的安全威胁，各国着力发展导弹防御技术。因此，针对上述导弹打击威胁，研究宽动态范围的红外辐射测量技术可以有效地解决饱和打击的手段，对防御体系建设具有重要的意义[1-2]。国内对红外辐射特性测量的研究已经持续多年。特别是辐射定标方面，许多研究团队一直从事该方面的工作：杨词银等基于800 mm高精度面源黑体的对地基大口径红外系统进行辐射定标，并分析了实验误差[3]；唐嘉等提出了多种红外辐射定标的方法，包括扩展源定标、间接定标和点源定标，并分析了各自的优缺点[4]。在辐射测量方面，吕游等提出双波段辐射测量算法，都推动了目标红外辐射特性的发展。而现在针对宽动态的辐射测量研究相对较少，对红外辐射特性测量系统，其所谓的宽动态就是要求系统能够实现从低温到高温的测量，获取不同温度的目标的不同的红外辐射特性，利用红外辐射特性的差异，进而实现对目标的发现与识别[5-9]。
为研究宽动态的辐射测量的精度。文中首先介绍了制冷型红外光电探测系统的定标原理。在宽动态范围的辐射定标的基础上，提出了宽动态范围的二次辐射修正方法。并基于600 mm口径的中波红外辐射特性测量了系统外场，采集数据进行了精度验证，对修正前和修正后的辐射测量的精度进行了比对，证实了宽动态辐射测量修正的必要性。
-
假设入射到红外测量系统的光子数为Np，光子辐射所激发的电荷数为Ne则探测器的光电转化效率η(λ)为[10]：
$$\eta {\rm{(}}\lambda {\rm{)}} = \dfrac{{{N_{\rm{e}}}}}{{{N_{\rm{p}}}}}$$ (1) 若探测器单个像元面积为A，在曝光时间Tint
内，则目标的辐射出射度M (单位为W/m2)与其光子数Ne之间的关系为： $$M(\lambda ,T) = \dfrac{{h \cdot \upsilon \cdot {N_{\rm{p}}}}}{{A \cdot {T_{{\rm{int}}}}}} = \dfrac{{h \cdot c \cdot {N_{\rm{e}}}}}{{A \cdot {T_{{\rm{int}}}} \cdot \lambda \cdot \eta (\lambda )}}$$ (2) 式中：c为光速，其值2.99×108 m/s；h为普朗克常数，其值为6.62×10−34 Js。
对朗伯体来说，满足：
$${N_{\rm{e}}}(\lambda ) = \dfrac{{A \cdot {T_{{\rm{int}}}} \cdot \lambda \cdot \text{π} \cdot \eta (\lambda )}}{{hc}} \cdot L(\lambda ,T)$$ (3) 给出了理想情况下，目标辐射亮度与激发电荷的关系。
对于带镜头的光学系统来说，波段响应λ1~λ2的范围内，每个像元上产生的灰度G （单位为DN），与黑体辐射亮度的关系为：
$$G = \int_{{\lambda _1}}^{{\lambda _2}} {{\tau _0}} \dfrac{{a \cdot A \cdot {T_{{\rm{int}}}} \cdot \lambda \cdot \text{π} \cdot \eta (\lambda )}}{{4{F^2}hc}} \cdot L(\lambda ,T){\rm{d}}\lambda + B$$ (4) 式中：F为光学系统的光圈数，定义为f/D，f为系统的焦距，D为光学系统的入瞳直径；τ0为光学系统的透过率；a为电子放大系数；B为光学系统和红外探测器产生的噪声偏置，单位为DN。
令
$k = a \cdot \dfrac{{A \cdot \text{π} }}{{4{F^2}}} \cdot {\tau _0}$ ，红外辐射测量系统的光谱响应率R表述为$\displaystyle\int_{{\lambda _1}}^{{\lambda _2}} {\dfrac{{\eta (\lambda ) \cdot \lambda }}{{hc}}} {\rm{d}}\lambda$ ，而在中波窄波段的光电转化效率几乎为常数，$\dfrac{\lambda }{{hc}}$ 为窄波段单位能量中的光子数，也是常数，则上式简化为：$$G = k \cdot {T_{{\rm{int}}}} \cdot R\int_{{\lambda _1}}^{{\lambda _2}} {L(\lambda ,T)} {\rm{d}}\lambda + B$$ (5) 图1为传统辐射定标的基本原理。
图 1 辐射定标能量传递原理
Figure 1. Principle of energy transfer in radiation calibration
-
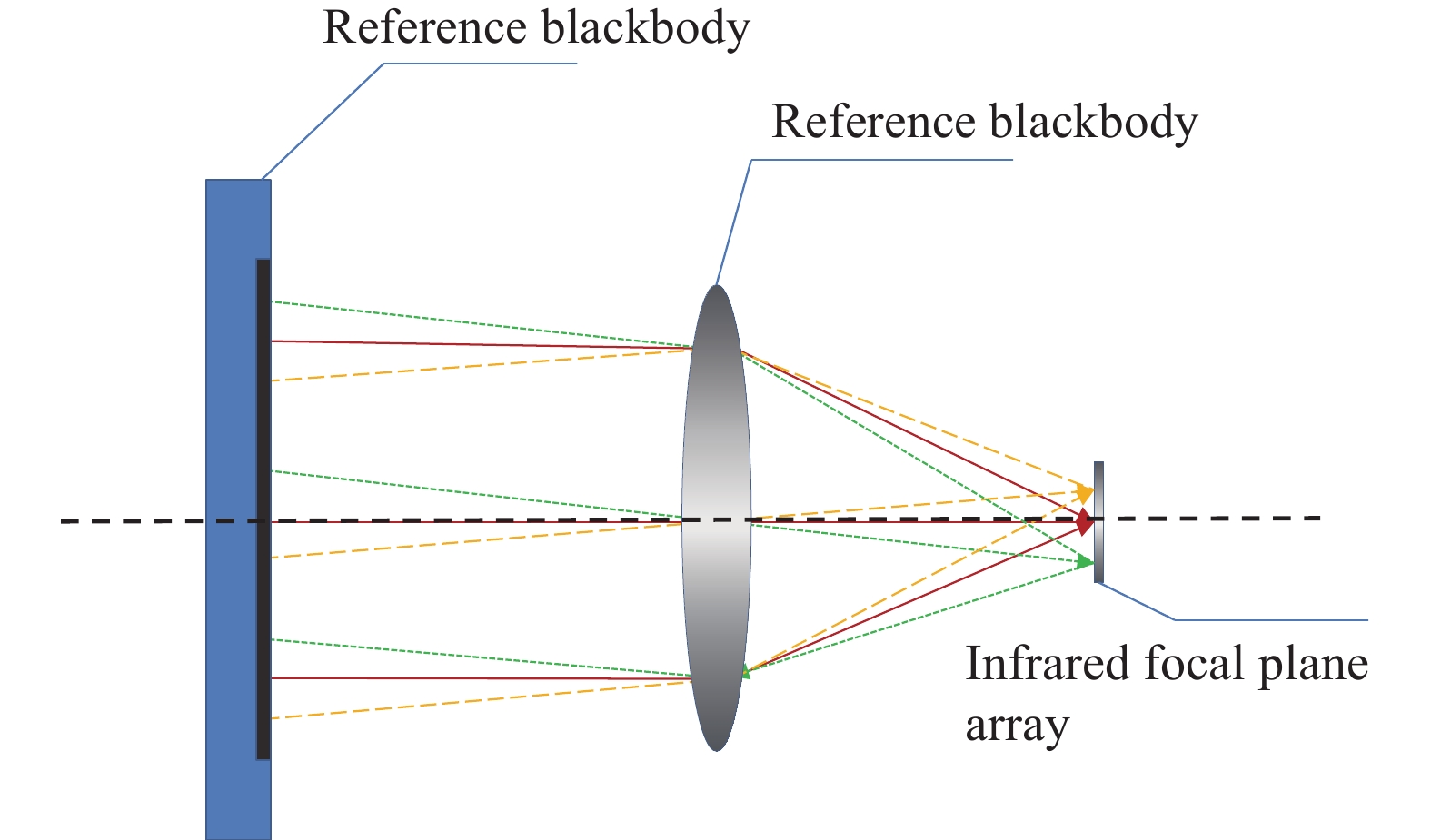
宽动态的辐射定标是实现宽动态红外辐射特性测量的基础。而现在传统的面源黑体（温度最高为400 ℃）定标很难满足宽动态辐射测量的需求。平行光管定标法是最为常见的宽动态定标方法之一，利用平行光管实现对高温腔型黑体的均匀扩束，如图2所示。高温腔型黑体配合平行光管更容易实现高温定标（1200 ℃）。
图 2 平行光管定标原理示意图
Figure 2. Schematic diagram of collimator calibration principle
同样平行光管相比面源黑体定标也带来了更多的定标误差。主要是由于平行光管自身的透过率和高温定标需要采用的中性衰减片的影响。因此要实现高精度宽动态范围的辐射定标与测量，需要对平行光管和中性衰减片对定标与测量带来的误差进行修正，其原理如下。
在理论透过率τ100%下，系统的辐射定标方程为：
$$\begin{split} {G_1} = &{T_{{\rm{int}}}} \cdot {{R'}_1}\int_{{\lambda _1}}^{{\lambda _2}} {L(\lambda ,T)} {\rm{d}}\lambda + {B_1} =\\ & k \cdot {T_{{\rm{{\rm{int}}}} }} \cdot {\tau _{100\% }} \cdot R\int_{{\lambda _1}}^{{\lambda _2}} {L(\lambda ,T)} {\rm{d}}\lambda + {B_1} \end{split} $$ (6) 式中：τ100%为衰减片的透过率；
${R'_1}$ 为低温段拟合系数。在高温段，相同的衰减片τ100%下，平行光管辐射定标方程为：
$$ \begin{split} {G_2} =& {T_{{\rm{int}}}} \cdot {{R'}_2}\int_{{\lambda _1}}^{{\lambda _2}} {L(\lambda ,T)} {\rm{d}}\lambda + {B_2} =\\ & k \cdot {T_{{\rm{int}} }} \cdot {\tau _{100\% }} \cdot {\tau _{{\rm{collimator}}}} \cdot R\int_{{\lambda _1}}^{{\lambda _2}} {L(\lambda ,T)} {\rm{d}}\lambda + {B_2} \end{split} $$ (7) 式中：τcollimator为平行光管的透过率；
${R'_2}$ 为高温段拟合系数。因此，修正后的平行光管的透过率表示为：
$${\tau _{{\rm{collimator}}}} = \dfrac{{{{R'}_2}}}{{{{R'}_1}}}$$ (8) 其次，由于在高衰减倍率的中性衰减片由于透过率较低，在不同的环境下，其透过率变化较大，因此需要对透过率进行标定，进行必要的修正。
将平行光管修正后的数据代入：
$$\begin{split} & {T_{{\rm{int}}}} \cdot {{R''}_2}\int_{{\lambda _1}}^{{\lambda _2}} {L(\lambda ,T)} {\rm{d}}\lambda + {B_2} =\\ & k \cdot {T_{{\rm{int}} }} \cdot {\tau _{100\% }} \cdot \dfrac{{{{R'}_2}}}{{{{R'}_1}}} \cdot R\int_{{\lambda _1}}^{{\lambda _2}} {L(\lambda ,T)} {\rm{d}}\lambda \end{split} $$ (9) 切换到τfilter（τ filter≠100%），得到其他衰减片的平行光管定标方程为：
$$\begin{split} & {T_{{\rm{int}}}} \cdot {{R''}_3}\int_{{\lambda _1}}^{{\lambda _2}} {L(\lambda ,T)} {\rm{d}}\lambda = \\ & k \cdot {T_{{\rm{int}} }} \cdot {\tau _{{\rm{filter}}}} \cdot \dfrac{{{{R'}_2}}}{{{{R'}_1}}} \cdot R\int_{{\lambda _1}}^{{\lambda _2}} {L(\lambda ,T)} {\rm{d}}\lambda \end{split} $$ (10) 得到实际测量时，衰减片修正透过率τfilter为：
$${\tau _{{\rm{filter}}}} = \dfrac{{{{R''}_3}}}{{{{R''}_{}}_2}}$$ (11) 最终得到宽动态范围下的定标方程为：
$$\begin{split} {G_{}} = &k \cdot {T_{{\rm{int}} }} \cdot {\tau _{{\rm{filter}}}} \cdot {\tau _{{\rm{collimator}}}} \cdot R\int_{{\lambda _1}}^{{\lambda _2}} {L(\lambda ,T)} {\rm{d}}\lambda + B =\\ & k \cdot {T_{{\rm{int}} }} \cdot \dfrac{{{{R'}_2}}}{{{{R'}_1}}} \cdot \dfrac{{{{R''}_3}}}{{{{R''}_{}}_2}} \cdot R\int_{{\lambda _1}}^{{\lambda _2}} {L(\lambda ,T)} {\rm{d}}\lambda + B \end{split} $$ (12) -
如图3所示，地基红外辐射特性测量系统观测目标时接收的红外辐射包括：①经过大气衰减后的目标自身辐射；②目标表面反射周围环境的辐射；③地表散射的环境辐射；④大气程辐射。
图 3 红外辐射特性测量的基本原理
Figure 3. Basic principle of infrared radiation characteristic measurement
因此，宽动态范围的红外辐射测量表述为：
$$\begin{split} & G = \rho \cdot k \cdot \dfrac{{{{R'}_2}}}{{{{R'}_1}}} \cdot \dfrac{{{{R''}_3}}}{{{{R''}_{}}_2}} \cdot R({\tau _{{\rm{atm}}}} \cdot \int_{{\lambda _1}}^{{\lambda _2}} {(L(\lambda ,{T_0})} + L({T_{{\rm{path}}}})){\rm{d}}\lambda ) + \\ & B + (1 - \rho ) \cdot \int_{{\lambda _1}}^{{\lambda _2}} {L(\lambda ,{T_{\rm{b}}})} {\rm{d}}\lambda \end{split} $$ (13) 式中：ρ为被测目标的反射率；L(λ,T0
)为被测目标的光谱辐射亮度；τatm和L(Tpath)分别为大气透过率和大气程辐射；L(λ,Tb)为背景的光谱辐射亮度。利用大气传输修正系统获取大气透过率和大气程辐射。 -
为验证二次修正对宽动态范围的红外辐射测量精度影响，利用口径600 mm中波红外辐射测量系统进行辐射定标和测量实验。其采用系统的参数见表1，系统定标采用高精度的常规面源黑体，黑体发射率为0.94，温度范围为0~100 ℃，辐射面积为700 mm ×700 mm，温度精度为0.01 ℃。高温腔型黑体辐射面为25.4 mm，温度范围50~1200 ℃，发射率为0.99，温度步长为50 ℃，温度精度为0.01 ℃。
表 1 红外系统的参数表
Table 1. Parameters of infrared system
Parameters Value Band/μm 3-5 Depth/bit 14 Pixel size/μm2 15 ×15 Pixel number 640×512 Focal length/mm 1200 Aperture/mm 600 中低定标采用常规面源黑体，控制面源黑体从20 ℃升温至100 ℃，温度采样步长为5 ℃。系统采集图像所用的积分时间为1 ms，拟合定标结果如图4所示。
图 4 辐射定标结果
Figure 4. Radiation calibration results
中波1 ms低温结果为：
$$ G = 340.496\;7\times L(T) + 16\;189.174\;63$$ (14) 在0.5 ms得到全透高温中波定标结果为：
$$y = 160.273\;66 x + 712.577\;63$$ (15) 根据公式（9）和公式（10），得到在当时测试环境下，实际光管的透过率为0.9806。
-
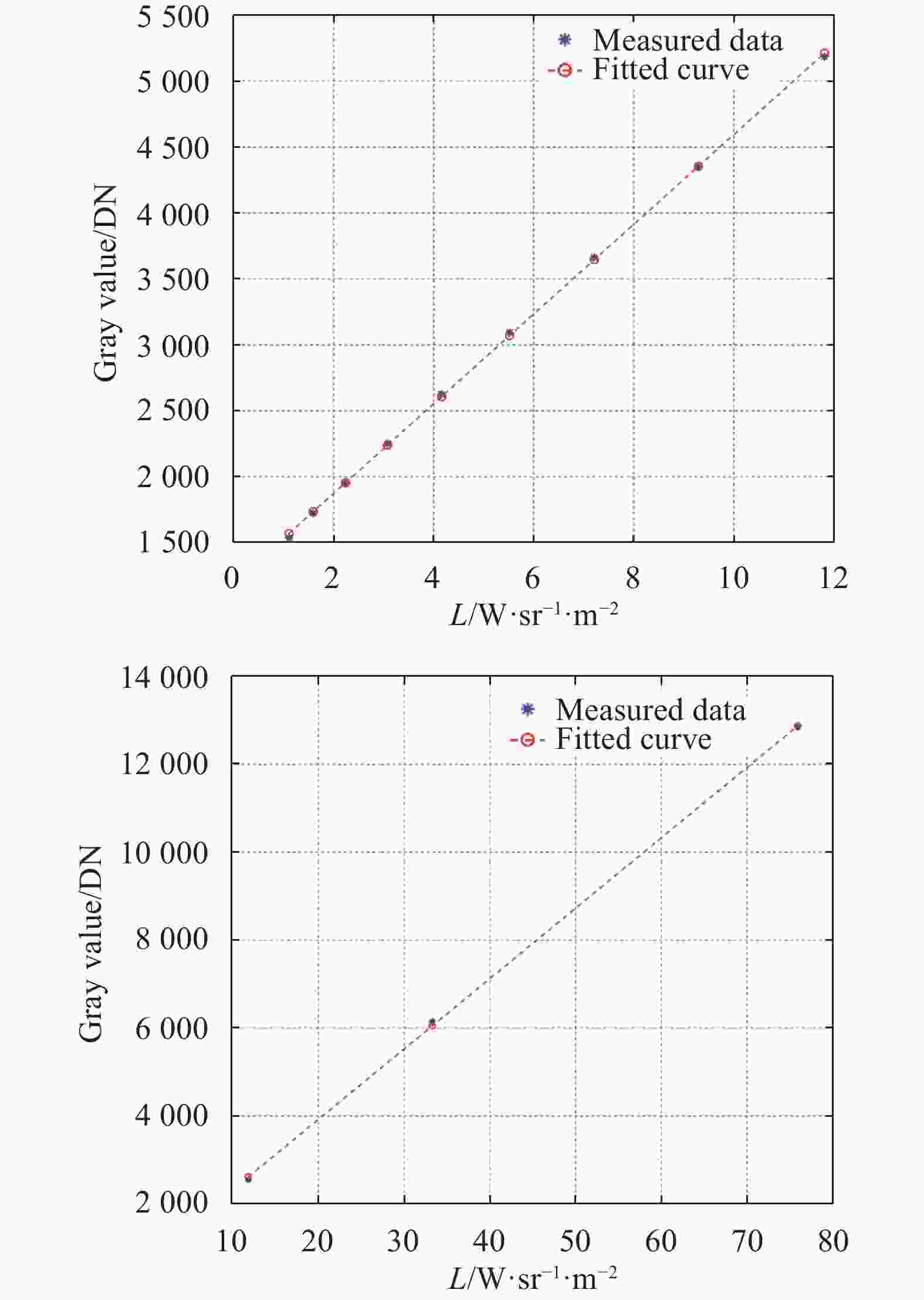
在获取光管的透过率后，获取实际在100%，50%，20%，10%，2%衰减下的定标结果如表2所示，其数据拟合结果如图5所示。
表 2 不同档位的定标方程
Table 2. Calibration equations of different grades
Transmissivity Calibration equation 100% G=333.740 6×L(T)+1 071.849 50% G=163.873 1×L(T)+1 090.452 4 20% G=64.238 8×L(T)+1 127.514 2 10% G=41.309 4×L(T)+1 140.888 5 2% G=10.269 8×L(T)+1 326.024 8 
图 5 不同衰减倍率下的辐射定标数据
Figure 5. Radiation calibration data at different attenuation ratios
在不同透过率下实际得到的衰减片的透过率如表3所示。在不同的透过率下可以看出，衰减倍率越高其相对误差也越大，主要是衰减倍率高，其反射率较大，受环境温度影响较大。
表 3 实际修正后透过率
Table 3. Actual corrected transmittance
Ideal transmissivity Actual transmissivity Error 50% 49.08% 2.44% 20% 19.24% 3.5% 10% 12.37% 29.1% 2% 3.06% 60.5% -
为验证平行光管和衰减片修正结果可以有效地提高宽动态范围的红外辐射测量的精度。采用上述红外辐射测量系统系统进行验证，目标距离系统770 m，大气透过率和大气程辐射采用修正系统如表4所示。
表 4 测量实验气象条件
Table 4. Meteorological conditions of measurement experiment
Parameters Value Wind speed/m•s-1 7.1 View angle/(°) 0 Pressure/hPa 905 Visibility/km 20 km Humidity 26.2% 计算得到的大气修正数据为：
$$\begin{split} & {\tau _{{\rm{atm}}}} = 0.731\;7 \\ & {L_{{\rm{path}}}} = 0.207\;5\;{\rm{W}} \cdot {{\rm{m}}^{ - 2}}\cdot {\rm{s{r}}^{ - 1}} \end{split} $$ (16) 系统分别在2%，10%，20%衰减片下采集200~600 ℃的目标，得到在不同衰减片下的修正与未修正的对目标的测量精度。辐射测量实验时记录的环境条件（测量当天阴天）见表4。
在理论衰减倍率为2%，修正前测量绝对误差平均值为20.26%，对衰减片的透过率修正后的误差为16.95%；在理论衰减倍率为10%，修正前测量绝对误差平均值为6.73%，对衰减片的透过率修正后的误差为4.09%；在理论衰减倍率为20%，修正前测量绝对误差平均值为3.41%，对衰减片的透过率修正后的误差为1.81%。最终的红外辐射测量数据如表5所示。
表 5 辐射测量数据对比
Table 5. Comparison of radiometric data
Ideal transmissivity Ideal temperature/℃ Ideal radiance/W·m−2·sr−1 Original radiance/W·m−2·sr−1 Revised radiance/W·m−2·sr−1 20% 200 72.852 77.744 2 72.937 4 300 252.867 252.544 5 247.573 1 400 609.562 618.075 7 607.692 3 500 1 173.579 Saturation Saturation 600 1 947.853 Saturation Saturation 10% 200 72.852 78.777 6 75.772 1 300 252.867 265.334 3 245.248 1 400 609.562 618.466 2 602.986 3 500 1 173.579 1 028.563 0 949.088 1 600 1 947.853 Saturation Saturation 2% 200 72.852 81.713 7 75.987 0 300 252.867 251.830 1 237.028 9 400 609.562 600.893 0 598.888 8 500 1 173.579 1 195.297 7 1 168.865 7 600 1 947.853 2 008.890 6 1 998.229 2 -
文中针对宽动态范围的红外辐射特性需求，首选推导了红外辐射定标的基本原理，针对宽动态的辐射定标修正，提出宽动态测量平行光管透过率修正方法和衰减片透过率修正方法。并采用600 mm的中波红外系统进行辐射定标验证。实验结果表明，对平行光管的透过率和衰减片的透过率进行修正可以有效地提高辐射特性测量的精度，具有一定的工程应用价值。
Improvement of wide dynamic infrared radiation measurement accuracy based on dual correction
-
摘要: 随着高超音速武器的出现，实现系统对目标从低温到高温宽动态的辐射测量是未来的发展趋势，而现在对辐射测量宽动态范围的研究相对较少。文中针对宽动态辐射测量中的平行光管和衰减片带来的误差提出了二次修正方法，进一步提高了高温红外辐射测量的目标反演的精度。为验证文中提出方法的实际效果，对基于600 mm口径的中波红外辐射测量系统进行了实验。并利用文中的方法对2%、10%、20%的辐射测量结果进行了修正，实验分析结果显示，该修正方法分别将原有的测量精度提高3.31%、3.27%、1.60%，证实修正方法可以有效地提高辐射测量的精度，具有一定的工程实践意义。Abstract: With the appearance of hypersonic weapon, it is a coming tendency to measure radiation in wide dynamic range from low temperature to high temperature. At present, the research of wide dynamic range radiometric measurement is relatively few. In this paper, a dual correction of collimators and attenuators method was proposed for wide dynamic radiation measurement to further improve the accuracy of high temperature infrared radiation measurement. The experiment was carried out based on the mid-wave infrared radiation measurement system of 600 mm aperture. The radiation measurement results with attenuators 2%, 10% and 20% were corrected, and the original measurement accuracy was increased by 3.31%, 3.27%, 1.60% respectively. It is proved that the correction method can effectively improve the accuracy of radiation measurement, which has certain engineering practice significance.
-
图 3 红外辐射特性测量的基本原理
Figure 3. Basic principle of infrared radiation characteristic measurement
图 5 不同衰减倍率下的辐射定标数据
Figure 5. Radiation calibration data at different attenuation ratios
表 1 红外系统的参数表
Table 1. Parameters of infrared system
Parameters Value Band/μm 3-5 Depth/bit 14 Pixel size/μm2 15 ×15 Pixel number 640×512 Focal length/mm 1200 Aperture/mm 600 
下载: 导出CSV
表 2 不同档位的定标方程
Table 2. Calibration equations of different grades
Transmissivity Calibration equation 100% G=333.740 6×L(T)+1 071.849 50% G=163.873 1×L(T)+1 090.452 4 20% G=64.238 8×L(T)+1 127.514 2 10% G=41.309 4×L(T)+1 140.888 5 2% G=10.269 8×L(T)+1 326.024 8
下载: 导出CSV
表 3 实际修正后透过率
Table 3. Actual corrected transmittance
Ideal transmissivity Actual transmissivity Error 50% 49.08% 2.44% 20% 19.24% 3.5% 10% 12.37% 29.1% 2% 3.06% 60.5%
下载: 导出CSV
表 4 测量实验气象条件
Table 4. Meteorological conditions of measurement experiment
Parameters Value Wind speed/m•s-1 7.1 View angle/(°) 0 Pressure/hPa 905 Visibility/km 20 km Humidity 26.2%
下载: 导出CSV
表 5 辐射测量数据对比
Table 5. Comparison of radiometric data
Ideal transmissivity Ideal temperature/℃ Ideal radiance/W·m−2·sr−1 Original radiance/W·m−2·sr−1 Revised radiance/W·m−2·sr−1 20% 200 72.852 77.744 2 72.937 4 300 252.867 252.544 5 247.573 1 400 609.562 618.075 7 607.692 3 500 1 173.579 Saturation Saturation 600 1 947.853 Saturation Saturation 10% 200 72.852 78.777 6 75.772 1 300 252.867 265.334 3 245.248 1 400 609.562 618.466 2 602.986 3 500 1 173.579 1 028.563 0 949.088 1 600 1 947.853 Saturation Saturation 2% 200 72.852 81.713 7 75.987 0 300 252.867 251.830 1 237.028 9 400 609.562 600.893 0 598.888 8 500 1 173.579 1 195.297 7 1 168.865 7 600 1 947.853 2 008.890 6 1 998.229 2
下载: 导出CSV
-
[1] Chen Chuan, Yi Weining, Cui Wenyu. Measurement of infrared radiation characteristics of spatial target based on reference source [J]. Infrared and Laser Engineering, 2018, 47(8): 0804004. (in Chinese) [2] Wang Jianjun, Huang Chen, Li Jianting. Calibration technology of infrared radiation measurement for space object [J]. Infrared & Laser Engineering, 2016, 45(4): 0404002. (in Chinese) [3] Yang Ciyin, Cao Lihua. Radiation calibration and error analysis for a large-aperture infrared opto-electric system [J]. Infrared and Laser Engineering, 2011, 40(9): 1625-1629. (in Chinese) [4] Sun Zhiyuan, Chang Songtao, Zhu Wei. Simplifying method of radiance calibration for MWIR detector [J]. Infrared and Laser Engineering, 2014, 43(7): 2132-2137. (in Chinese) [5] You Lü, Xin He, Wei Zhonghui, et al. Ambient temperature-independent dual-band mid-infrared radiation thermometry [J]. Applied Optics, 2016, 55(9): 2169-2174. doi: 10.1364/AO.55.002169 [6] Chang Songtao, Zhang Yaoyu, Sun Zhiyuan, et al. Method to remove the effect of ambient temperature on radiometric calibration [J]. Applied Optics, 2014, 53(27): 6274-6279. doi: 10.1364/AO.53.006274 [7] Bao Xingdong, Yu Xilong, Mao Hongxia, et al. Search on fluid field and infrared radiation of vacuum plume based on theoretical analytical method [J]. Infrared and Laser Engineering, 2020, 49(1): 0104003. (in Chinese) [8] Tian Qijie, Chang Songtao, Qiao Yanfeng, et al. Radiometric calibration based on low-temperature area blackbody for infrared systems with high dynamic range [J]. Acta Photonica Sinica, 2017, 46(4): 0412003. (in Chinese) doi: 10.3788/gzxb20174604.0412003 [9] Li Zhou. Research on ground-based infrared characteristics measurement systems in wide range radiometry[D]. Changchun: Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, 2018. (in Chinese) [10] Li Zhou, Qiao Yanfeng, Chang Songtao, et al. High-speed calibration algorithm for wide dynamic range infrared radiometric system [J]. Infrared & Laser Engineering, 2017, 46(6): 0617003. (in Chinese) -
点击查看大图
计量
- 文章访问数: 299
- HTML全文浏览量: 48
- PDF下载量: 27
- 被引次数: 0
