-
电子散斑干涉测量技术(electronic speckle pattern interferometry,ESPI) 是一种全场、非接触、高精度的光学测量方法。在材料和结构的缺陷检测、三维变形、应力应变测量、振动分析方面有广泛的应用[1-3]。激光散斑干涉测量是通过测量散斑干涉信号的相位变化来精密测量粗糙物体表面的变形的检测方法。在相干激光照明下,把待测表面漫反射所形成的散斑场和固定且不变形的某一散斑场叠加,构成一个新的散斑场。待测表面发生变形使叠加而成的散斑场也发生变化,变形体表面每移动1/2波长的距离,光斑的明暗变化就形成一个循环。当物体表面有不均匀的离面位移时,凡是位移为1/2波长及其整数倍的地方,散斑仍是原来的状态,将变化前后散斑图相减,暗部显示变形前后散斑完全相同的区域,亮部显示变形前后散斑不相同的区域,因此,这块区域变化能以干涉条纹形式显示出来。干涉条纹中包含相位变化信息,经相位计算可将干涉条纹图转化为干涉相位图,此时干涉相位被限制、包裹在(−π, π]之间,要得到真实相位,需要利用解包裹算法进行解包裹处理[4-5]。
枝切法(branch-cut,BC)是激光散斑干涉相位图解包裹的常用方法。它能识别残差点,防止误差传递,具有解缠精度高、实现简单等优点,是业内公认的经典解包裹算法[6]。由于激光器和检测方法的固有缺陷,激光散斑干涉相位图中必然会存在噪声,无法完全避免,其数量取决于激光器的性能和检测环境[7]。当激光散斑干涉相位图中存在较多散斑噪声、信噪比差时,枝切线密集,容易形成环路,从而导致部分区域无法解包裹而形成“孤岛区域”,出现拉丝和斑块现象,同时增大了计算量,导致解包裹速度缓慢,影响了枝切法在实际测量中的工程化应用[8]。
文中针对以上问题提出了基于Goldstein枝切法解包裹的优化方案,利用残差点电磁力和小区域明暗分界线方向关系,对残差点所在小区域进行多轮图像平滑处理或增加明暗跳变操作,快速消除相位图内的残差点,采用GPU加速技术大幅缩短图像处理时间。通过仿真试验和实验应用证明文中方案能有效地减少图像残差点对枝切法解包裹的干扰、提高运算速度,满足工业应用的性能要求。
-
散斑相位图解包裹通过公式(1)来获得:
$$\varphi (r)=\int_c^{} {\nabla \psi {\rm d}r + } \varphi ({r_0})$$ (1) 式中:
$\varphi (r)$ 为像素r上的解包裹相位;$\varphi ({r_0})$ 为像素点${r_0}$ 上的已知解包裹相位;$\nabla \psi $ 为包裹相位;$c$ 为积分路径。从上式可以看出要使计算出的$\varphi (r)$ 相同,就要求积分过程与积分路径$c$ 无关,而实际相位图部分像素点由于存在相位噪声并且有欠采样等问题,使得经过这些像素点的积分有时候会大于π,出现错误的相位结果。如何选择积分路径是解包裹算法的关键,其中枝切法是解决这个问题的重要算法。枝切法是由美国喷气推进实验室的Goldstein等人于1986年提出,也称Goldstein枝切法。其主要步骤:识别残差点、放置枝切线、避开枝切线标识进行路径解包裹。残差点通过判断是否满足ITOH条件来获取[9],放置枝切线和避开枝切线解包裹处理流程如图1所示。

图 1 枝切法解包裹流程。(a)解包裹;(b)放置枝切线
Figure 1. Process of branch-cut method. (a) Unwrapping process; (b) Placing branch lines process
该算法核心思路是识别干涉图像上的残差点,通过建立的枝切线将这些残差点连接起来,最后在相位展开过程中积分时避开枝切线,从而达到防止误差扩散、精准相位解包裹的目的。
-
在理想环境下相位图中残差点数量少,利用枝切法解包裹能得到理想结果图,但在普通车间生产环境中由于外来光线干扰、激光器长时间运行性能下降、相机拍照局部点欠采样等原因,获取的相位图中残差点数基本都是数百个以上,即使滤波也不能完全消除,在残差点分布密集的地方枝切线容易闭合,形成孤立区域,出现区域性解包裹误差[10]。残差点数量直接影响枝切线的计算量,假设正负残差点的个数分别为
$n$ ,那么组合生成的枝切线最多就有$n!$ 种情况。当残差点数目较大时,利用枝切法解包裹速度非常慢。实验发现500万像素相位图中含200个以上的残差点时,其解包裹处理平均耗时需15 s左右,求出的枝切线长度长、形状复杂,容易形成环路,出现大块“拉丝”和“斑块”现象。文中采用电磁力导引消除残差点的方法减少残差点总量,降低相位噪声和欠采样点解包裹干扰,同时采用GPU并行加速计算技术,重新规划计算模型和任务单元,解决解包裹速度慢的问题。 -
将残差点当作带着正负单位电量的电子,将图片区域当作电磁力场,残差点之间相互引用或排斥。先根据受力公式求出各残差点受到外界的电磁力,然后以电磁力为导引,在明暗分界区域寻找电性相反的残差点,找到后中和电量,消掉这对残差点。多轮循环操作,快速消除残差点。其操作步骤为:
(1)输入散斑干涉相位图,通过Goldstein枝切法求出激光干涉散斑相位图中的所有残差点;
(2)根据受力公式求出当前每个残差点受到外界的电磁力,同时设定磁力阈值。受力公式定义如下:假若共有
$n$ 个残差点,则第k个残差点为${A_k}$ ,它受到外界(其他残差点)的电磁合力:$${F_{{A_k}}}=\sum\limits_{i=1}^n {{f_{{A_k}{A_i}}},(k!=i)} $$ (2) 其中
$$ {f_{{A_k}{A_i}}}=\left\{ {\begin{array}{*{20}{c}} {\dfrac{1}{{{{({D_{{A_k}{A_i}}})}^2}}},{\text{电性相反}}}\\ { - \dfrac{1}{{{{({D_{{A_k}{A_i}}})}^2}}},{\text{电性相同}}} \end{array}} \right. $$ (3) 式中:
$ {D_{{A_k}{A_i}}}{\text{为残差点}} {A_k} {\text{与}} {A_i} {\text{距离}}$ 。(3)在残差点所在小区域邻域内求出明暗分界线方向,以靠近明暗跳变大的一侧为正方向。其中亮域点组成亮域区域,暗域点组成暗域区域。
亮域重心坐标=亮域点坐标和的平均值
暗域重心坐标=暗域点坐标和的平均值
亮域区域与暗域区域边界线上的点为分界线点,经过亮域重心、暗域重心的直线垂直方向为明暗分界线方向,以靠近明暗跳变大的一侧为正方向。如图2所示,
${A_k}$ 为残差点,${E_{{A_k}}}$ 为${A_k}$ 对应的明暗分界线方向。(4)通过上述明暗分界线
${E_{{A_k}}}$ 方向和电磁力${F_{{A_k}}}$ 方向关系,依次对所有残差点所在小区域进行平滑处理或增加明暗跳变处理。当${E_{{A_k}}}$ 方向与${F_{{A_k}}}$ 方向夹角小于60°时,对该残差点小区域进行平滑处理;当夹角大于120°时,对该残差点小区域沿${E_{{A_k}}}$ 方向进行增加明暗跳变处理;当夹角大于60°而小于120°时,对该残差点小区域沿电磁力${F_{{A_k}}}$ 方向进行增加明暗跳变处理。其中平滑处理是指用残差点周围区域内点的平均灰度值来覆盖它原来的灰度值,在相位图上表现为分界线缩短;增加明暗跳变处理是经过残差点沿分界线方向或电磁力方向,对两侧区域中像素增加明暗跳变,在相位图上表现为分界线延长。具体操作为先对残差点邻域按公式
$$ w({{x,y}}) = \psi ({{x,y}}) + 2{{k}}\pi ,({{k}}{\text{为使}}0 \leqslant w({{x,y}}) < 2\pi {\text{的整数}}) $$ (4) 进行重包裹操作,使相位落在
$\left[ {0,2\pi } \right)$ 。然后对残差点邻域进行均值滤波,滤波之后根据公式$$ w'({{x,y}}) = w({{x,y}}) + 2{{k}}\pi ,\;\; ({{k}}{\text{为使}} {\rm{ - }}\pi \leqslant w({{x,y}}) < \pi {\text{的整数}}) $$ (5) 执行包裹操作,使相位重回到
$\left[ { - \pi ,\pi } \right)$ 区间。以图3为例,图中有4个残差点,A、B、D为负残差点,C为正残差点,从图像点特征可看出A、B两点电性相同,反向移动,B受力方向与分界线方向夹角小于60°,经过平滑处理,相位分界线缩短。C、D距离最近电磁力相吸,两点相向移动,相位分界线延长,进行增加明暗跳变处理。A点受力小于阈值,不移动。

图 3 残差点处理实例。(a) 处理前相位图;(b) 处理后相位图;(c) 各残差点受力方向与分界线方向
Figure 3. Example of residual point processing. (a) Phase diagram before processing; (b) Phase diagram after processing; (c) Direction of force and boundary line of each residual point
(5)生成处理后的散斑干涉相位图;
(6)重复步骤(1)~(5),直到所有残差点都消失或所受电磁力都小于等于某阈值时结束;经过以上处理后,大部分成对的异号残差点相互靠近,最后互相抵消。
上述方法会优先抵消空间距离近的残差点,处理效率高。同时可预设电场力阈值,当一个残差点电场力大于这个阈值时启动消除处理,对远距离的残差点影响较小,不会影响整体相位图质量。通过以上的步骤运算,可快速大幅减少相位图中残差点数量,进而降低后续解包裹的计算量。实验结果表明:对于高分辨率的相位图(大于500万像素),平均残差点去除率达98%以上,枝切线数量减少90%以上,对于噪点区域大、残差点密集的散斑相位图去残差点效果更加明显。图4为某高分辨率(2592×2 048)相位图的采用电磁力导引消除残差点后的图像结果,对整幅相位图残差点消除处理后,大部分残差点相互抵消,将残差点由885个减少到了14个,将解包裹枝切线数量由1047条减少到了19条。
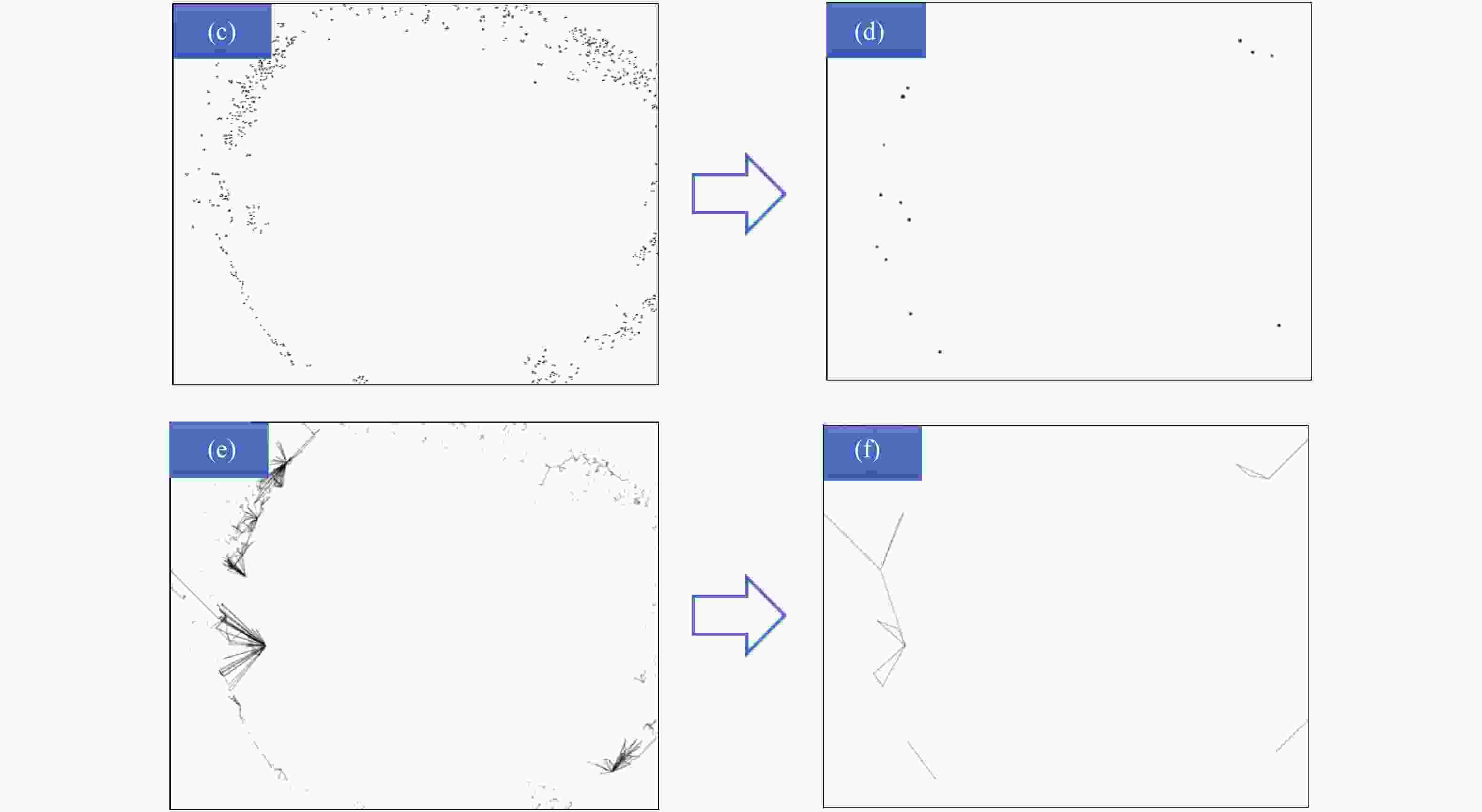
图 4 电磁力导引消除残差点效果实例。(a)原相位图;(b)处理后的相位图;(c)原相位图中的残差点(885个);(d)处理后的相位图中残差点(14个);(e) Goldstein解包裹方法枝切线(1047条);(f)改经后解包裹枝切线(19条)
Figure 4. Examples of removing residual points guided by electromagnetic force. (a) Original phase diagram; (b) Processed phase diagram; (c) Residual points in original phase diagram (885); (d) Residual points in processed phase diagram (14); (e) Branch lines in Goldstein unwrapping branch-cut (1047); (f) Branch lines in improved unwrapping branch-cut (19)
-
改进的枝切法可缩短放置枝切线的时间,但增加了消除残差点的时间,其过程受残差点总数、分布、电磁力阈值等因素影响,对整个图像解算提速作用不明显。在散斑干涉测量中图像处理分为以下几个阶段:(1) 相位提取(含求相位差); (2) 图像去噪处理(即滤波);(3) 相位解包裹。各阶段需要大量运算,随着图像处理规模的不断扩大,CPU运算能力已成为激光散斑干涉快速测量的瓶颈[11]。单核CPU运算能力不能满足应用需要,多核CPU提高了成本,增加系统实现难度,需要处理任务分割、多核CPU通信协作等繁琐问题。相比之下,GPU价格低廉,虽然单核处理能力较弱,但计算核心数量众多,数据处理逻辑简单,运算能力和存储带宽均远超CPU,适合大规模并行计算。散斑干涉测量相关计算基本都可用GPU并行计算加速。下面以正余弦均值滤波为例说明GPU并行计算技术应用方法。
正余弦均值滤波计算过程如下:对相位差图任意点(x, y),读取该点及邻域点的相位值
$ \theta $ ,先将其转换为相位的正余弦值$ {\rm{sin}}\theta $ 和$ {\rm{cos}}\theta $ ,然后选择滤波窗口对正余弦值进行均值滤波,再通过$\overline {\sin \theta } $ 和$\overline {\cos \theta } $ 计算$ \overline {\theta } $ ,重复以上步骤,得到图像较为平滑相位值$ \overline {\theta } $ 。当滤波窗口为3×3时,其滤波公式如下:$$\begin{split} \overline {\sin {\theta _{x,y}}} =& \dfrac{{\rm{1}}}{{{\rm{25}}}}\Bigg[ {\sin {\theta _{x,y}}{\rm{ + 3}}\left( {\sin {\theta _{x{\rm{ - 1}},y}} + \sin {\theta _{x{\rm{ + 1}},y}} + \sin {\theta _{x,y{\rm{ - 1}}}}} \right.} {\rm{ + }}\\ &\left. {\sin {\theta _{x,y{\rm{ + 1}}}}} \right){\rm{ + 2}}\left( {\sin {\theta _{x{\rm{ - 1}},y{\rm{ - 1}}}} + \sin {\theta _{x{\rm{ - 1}},y + 1}} + } \right.\\ &{\left. {\sin {\theta _{x + 1,y{\rm{ - 1}}}}{\rm{ + }}\sin {\theta _{x + 1,y{\rm{ + 1}}}}} \right)} \Bigg] \end{split} $$ (6) $$ \begin{split} \overline {\cos {\theta _{x,y}}} =& \dfrac{{\rm{1}}}{{{\rm{25}}}}\Bigg[ {5\cos {\theta _{x,y}} + 3\left( {\cos {\theta _{x{\rm{ - 1}},y}} + \cos {\theta _{x{\rm{ + 1}},y}} + \cos {\theta _{x,y{\rm{ - 1}}}}{\rm{ + }}} \right.} \\ &\left. {\cos {\theta _{x,y{\rm{ + 1}}}}} \right){\rm{ + 2}}\left( {\cos {\theta _{x{\rm{ - 1}},y{\rm{ - 1}}}} + \cos {\theta _{x{\rm{ - 1}},y + 1}} + } \right.\\ & {\left. {\cos {\theta _{x + 1,y{\rm{ - 1}}}}{\rm{ + }}\cos {\theta _{x + 1,y{\rm{ + 1}}}}} \right)} \Bigg] \end{split} $$ (7) 采用GPU并行计算加速时先将计算任务分割为互相独立的小任务,由多个互不依赖的线程同时处理。将图像分割为32×32的小块,每个小块及其外围一圈像素分配给一个线程块,即采用3×3窗口时,每个线程块分配34×34的小块,其中超出图像边界的部分采用镜像处理。对小块内像素的相位值分别求正弦和余弦值,然后采用公式(6)、(7)求得正余弦均值并通过反正切函数还原为相位。为提高计算效率,每个线程块内采用共享存储存取正余弦值。采用CUDA平台处理计算任务时,CPU与GPU交互如图5所示,将CPU作为控制器,负责读取数据,将数据传输给GPU;将GPU作为协作处理器,接收CPU传递的数据,在显存中开辟相应存储空间,存储传入的数据和中间处理数据,将这些数据分配给GPU上的多个线程进行处理,处理完成后,将数据传回CPU,由CPU进行后续处理。
-
为验证改进的枝切法的有效性,采用MATLAB工具对算法进行验证。在理想散斑相位图加入噪声,产生残差点,采用改进的枝切法进行解包裹,对比改进前后的解包裹图效果验证其有效性。以激光剪切散斑的干涉图为例,其定义函数如下:
激光干涉函数
$$\begin{split} c(j,i)=&(\cos (A{(j,i)^{}} + {{Q}} \times \cos {(A(j + {r_ - },i + {c_ - }))^2} + \\ &(\sin (A{(j,i)^{}} +{{Q}} \times \sin {(A(j + {r_ - },i + {c_ - }))^2} \end{split}$$ (8) 式中:
$A(j,i)$ 为随机相位;$({r_ - },{c_ - })$ 为剪切量;${{Q}}$ 为两束光照强度比。形变函数
$$\begin{split} &deform(j,i) =\\ &\left\{ {\begin{array}{*{20}{c}} {20 + i \times i \times 0.000\;1,\left( {{{j,i}}} \right) \notin {{U}}({j_0},{i_0})}\\ {\sqrt {({{({i_0} - i)}^2} + {{({j_0} - j)}^2})} /5 + i \times i \times 0.000\;1,\left( {{{j,i}}} \right) \in {{U}}\left( {{j_0},{i_0}} \right)} \end{array}} \right. \end{split}$$ (9) 式中:
$U({j_0},{i_0})$ 为以$({j_0},{i_0})$ 点为中心的形变区域。当干涉相位图大小为1000×1000,在公式(8)中Q取值为0.9,水平方向设置剪切量 (
${r_ - }{\rm{=}}0,{c_ - }{\rm{=}}80$ ),随机选9个不同大小的形变区域,按照公式(9)形变处理,可得到激光剪切散斑干涉相位图,如图6(b)所示,在相位图条纹交界区域选100个点做小范围平滑处理,破坏相位正常跳变,产生残差点,其效果如图6(c)所示。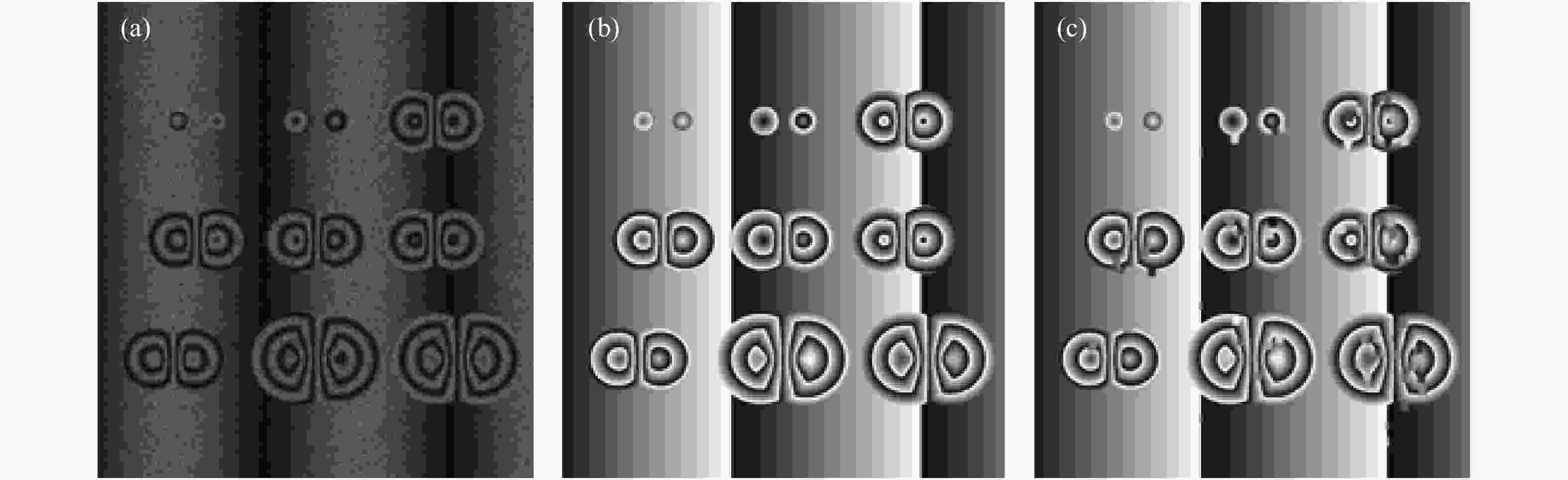
图 6 仿真图。(a)散斑图;(b)相位图;(c)含残差点的相位图
Figure 6. Simulation diagram. (a) Speckle pattern; (b) Phase diagram; (c) Phase diagram with residual points
采用改进前后的枝切法解包裹,其结果如图7所示。通过对比可以看出,使用Goldstein法求得相位图包括124个残差点,建立的枝切线长度较长,并且在残差点密集的区域形成枝树,而利用文中的方法将残差点消除到了4个,不仅枝切线的数量少、长度短,且没有形成枝切树,从图7(c)和图7(d)的最终展开结果也可以看出采用Goldstein法由于枝切线问题,导致部分区域相位解包裹效果很差,且存在大块未解开的区域,而文中方法展开的效果较好,能看到明显的形变区域。

图 7 两种枝切法解包裹对比。(a) Goldstein枝切法求得的枝切线;(b) 改进后枝切法求得的枝切线;(c) Goldstein枝切法解包裹图;(d) 改进后枝切法解包裹图
Figure 7. Comparison of the two branch-cut methods. (a) Branch lines in Goldstein branch-cut method; (b) Branch lines in improved branch-cut method; (c) Unwrapping diagram in Goldstein branch-cut method; (d) Unwrapping diagram in improved branch-cut method
枝切法是基于路径跟踪的相位解包裹算法,采用避开干扰区域(枝切线区域),选择质量好的区域优先解包裹,因此不会将局部误差向整体图像扩散,具有更高的解包裹精度,但枝切法很少能消除所有残差点,生成的枝切线影响解包裹图的整体平滑度和计算速度。枝切法属于局部法解包裹算法,不同于整体法解包裹算法。整体法是将相位解包裹问题转化为求解数学最小范数极值问题,如最小二乘法、正余弦变换解包裹、快速傅里叶变换解包裹等,此类方法是通过计算解包裹前后相位梯度的最小均方误差,求最接近于真实值的解包裹相位,每个像素点的解包裹结果都是近似值,它求得解包裹图更平滑,计算速度更快[12]。相比而言,枝切法适合高精度定量测量,如测量表面形变等,而对于精度要求不高的测量(如判别复合材料缺陷位置等),采用最小二乘法等整体解包裹算法效果更好。
-
改进后枝切法总体上采用Goldstein枝切法解包裹流程,重点对相位图进行预处理消除残差点,算法实现包括以下要点。
(1) 电磁力计算函数,以整张图片(或选择图片区域)为计算对象,按像素密度找到所有残差点,记录其坐标和正负标识。按公式(2)、(3)分别求出每个残差点合力(包含大小和方向)。函数定义核心逻辑如下(以C语言编程为例):
Void Electric Force()
{
…
float dist=sqrtf((forces[j].ec.x-forces[i].ec.x)*(forces[j].ec.x−forces[i].ec.x)+
(forces[j].ec.y−forces[i].ec.y)*(forces[j].ec.y-forces[i].ec.y));
f.fx=(forces[j].ec.x-forces[i].ec.x)/(dist*dist);
f.fy=(forces[j].ec.y−forces[i].ec.y)/(dist*dist);
if(forces[i].ec.pol==forces[j].ec.pol)
{
f.fx*=−1;
f.fy*=−1;
}
forces[i].fx+=f.fx;
forces[i].fy+=f.fy;
…
} //其中forces[]为残差点合力数组,ec为残差点电量数据结构,包括坐标x,y,正负标识pol,i,j为残差点的序号,f为电磁力。
(2) 残差点移动函数,遍历所有残差点,沿各自受力方向(和分界线位置关系)按像素移动,空出位置采用平滑和增加明暗跳变处理,函数定义核心逻辑如下:
bool Move Wind Point By EF(float MinF)
{
…
//若合力与分界线夹角小于60°或大于120°
…
if(fx*dirx+fy*diry>0)//合力与分界线方向相符,采用平滑处理
{
..
avrd=(local_d[j−1][i−1]+local_d[j−1][i]+local_d[j−1][i+1]+
local_d[j][i−1]+local_d[j][i]+local_d[j][i+1]+
local_d[j+1][i−1]+local_d[j+1][i]+local_d[j+1][i+1])/9;
local_d[j][i]=avrd;
..
}
else //合力与分界线方向相反,增加明暗跳变处理
{
avrd=(local_d[j−1][i−1]+local_d[j−1][i]+local_d[j−1][i+1]+
local_d[j][i−1]+local_d[j][i]+local_d[j][i+1]+
local_d[j+1][i−1]+local_d[j+1][i]+local_d[j+1][i+1]);
if (local_d[j][i]<128)
{
avrd-=256*count_skip;
}
else
{
avrd+=256*count_skip;
}
avrd/=9;
local_d[j][i]=avrd;
…
}
} //其中local_d[j][i]为待处理残差点相位值,count_skip为跳变次数。
(3)电磁力阈值(MinF),大多情况下残差点不能完全消除,为防止程序死循环,需要设置电磁力阈值,用于终止遍历过程,电磁力阈值设值大,会提早跳出循环,留下不处理的残差点过多,电磁力阈值设值小,会产生无效循环,耗费时间。实验发现设为0.0002~0.0005较为合适,同时设置最大循环次数辅助逻辑判断,效率更高。
(4) GPU并行计算要点,采用GPU并行计算时速度瓶颈大多出现在数据传输阶段,包括系统内存与GPU显存间的传输、GPU核心与显存间的传输、线程块内共享内存的读写和线程块与全局显存间的读写。数据传输量越少、显存读写连续性越好,越有利于发挥GPU计算速度快的优点。算法实现时应尽可能减少GPU与CPU的数据传递,为消除解包裹前期冗余的数据的传送过程,可将相位提取(求相位差)与滤波合并计算。此外,性能不同的GPU可以采取不同的算法在计算速度和精度之间取得平衡。对性能较低的GPU,可以适当降低精度要求,采用正余弦均值滤波通过减少滤波次数的方式提高滤波速度,保证实时性;对于性能较强的GPU,可以采用如Butterworth低通滤波等大计算量算法来同时获得较好的滤波效果和图像处理的实时性。
-
搭建迈克尔逊剪切散斑干涉测量系统(见图8),采用德国Basler scA2500-60 μm工业相机,CCD靶面尺寸1″,成像镜头采用焦距为12 mm、靶面尺寸1″的日本moritex镜头,光源采用波长为532 nm的单纵模绿光激光器,被测物为500 mm×300 mm×30 mm、表面粘贴0.5 mm铝合金蒙皮的蜂窝夹层结构标准试件,其内预置有Ф40 mm、Ф20 mm和Ф15 mm的三种脱胶点。

图 8 系统测量装置。(a)测量平台及场景;(b)迈克尔逊剪切装置;(c)被测物
Figure 8. System measurement device. (a) Measurement platform and scene; (b) Michelson shearing device; (c) Measured object
将标准试件固定,利用吹风机均匀加热,随着样板表面温度的降低,样板表面出现连续形变,采用“四步相移法”[1]随机拍得标准试件形变前后各4幅500万像素(2592×2 048)的散斑图。通过四步相移求相位公式,计算求得相位图。采用正余弦滤波算法经过20次滤波后,得到清晰的相位图。以该图为输入,采用传统枝切法和文中优化后的枝切法进行解包裹。得到结果如图9所示。

图 9 枝切法解包裹。(a)变形前4幅散斑图;(b)变形后4幅散斑图;(c)原始相位图;(d)滤波后相位图;(e)传统枝切法解包裹图;(g)改进后枝切法解包裹图
Figure 9. Unwrapping by branch-cut method. (a) The four speckle diagrams before deformation; (b) The four speckle diagrams after deformation; (c) Original phase diagram; (d) The phase diagram after filtering; (e) Unwrapping diagram by traditional branch-cut method; (g) Unwrapping diagram by improved branch-cut method
从图9可以看出,两种解包裹算法从整体上都能观察到缺陷的位置和大小,但优化后枝切法解包裹算法由于提前进行了残差点消除处理,它的结果图中几乎没有拉丝和斑块现象,图像质量明显更优。
在速度方面,基于intel i7-6500U CPU@2.5 GHz 处理器、NVIDIA GeForce 940MX@1004 MHz显卡,采用单一CPU图像计算和利用GPU并行计算两种方式,对图9中原始图进行求相位、滤波、解包裹操作,表1为图像处理耗时分布。
表 1 相位图处理计算总耗时
Table 1. Computing time of phase diagram processing
Operate Parameters Time consuming/ms CPU GPU Phase calculation 5 million pixels 719 148 sin-cos filtering “3×3”,20 times 17571 403 Branch-cut unwrapping 89 residual points 1142 901 由于求相位、滤波相对解包裹处理逻辑更简单,整体是以单个像素点为对象单独计算,计算中CPU、GPU之间数据交互少,速度提升更显著。采用GPU并行计算处理时间均控制在1500 ms以内,满足了高分辨率散斑图快速计算的工程应用需要。
-
文中针对传统枝切法在由于外来光线干扰、激光器性能下降、相机拍照局部点欠采样等原因经常出现的枝切线密集、计算速度慢等问题,在Goldstein枝切法的基础上引入了残差点电磁场的概念,提出了利用电磁力导引消除残差点的方法,所提到的方法可快速消除绝大多数残差点,减少解包裹计算量和产生形状复杂、长枝切线,形成环路的现象,提高枝切法解包裹的成功率,同时通过GPU并行计算加速方法,提升高分辨率散斑图解算速度。仿真实验和实际测量数据表明优化后枝切法解包裹图像质量更好,对于500万像素散斑相位图,通过电磁力导引可消除98%以上的残差点,减少90%以上的枝切线,处理时间可由以往15 s压缩至1.5 s,实现了枝切法在激光散斑干涉相位图解包裹中工程化应用。
Application of improved branch-cut method in speckle phase unwrapping
-
摘要: 为了实现枝切法在激光散斑干涉相位图解包裹中工程化的应用,解决由于外来光线干扰、激光器性能下降、相机拍照局部点欠采样等原因出现的枝切线密集、计算速度慢等问题,在Goldstein枝切法的基础上提出了优化改进方案。将残差点当作带着正负单位电量的“电子”,利用电磁力导引通过相位平滑或增加相位跳变处理消除残差点,减少枝切线数量,同时采用GPU并行计算技术提高图像处理速度。仿真实验和实际测量数据表明优化后 的枝切法解包裹图像质量更好,对于500万像素散斑相位图,通过电磁力引导可消除98%以上的残差点,减少90%以上的枝切线,处理时间可由以往15 s压缩至1.5 s,满足了枝切法高质量快速解包裹的工程化应用要求。Abstract: In order to realize the engineering application of the branch-cut method in the phase diagram unwrapping of laser speckle pattern interferometry, and to solve the problems of dense branch lines and slow calculation speed caused by the interference of external light, the degradation of laser performance and the undersampling of local points taken by cameras, an optimization and improvement scheme based on Goldstein branch-cut method was proposed. The residual points were regarded as "electrons" with positive and negative unit electric quantities, guided by electromagnetic force, and eliminated by phase smoothing or increasing phase jump, thus reducing the number of branch lines. At the same time, GPU parallel computing technology was adopted to improve the processing speed of high-resolution and large-size phase diagram. The simulation experiment and actual measurement data show that the unwrapping diagram quality is better by the improved branch-cut method. For the 5 million pixel speckle phase diagram, more than 98% of the residual points can be eliminated by electromagnetic force, and the branch lines can be reduced by more than 90%. The processing time can be reduced from the previous 15 seconds to 1.5 seconds, which meets the engineering application requirements of high quality and quick unwrapping by branch-cut method.
-
图 4 电磁力导引消除残差点效果实例。(a)原相位图;(b)处理后的相位图;(c)原相位图中的残差点(885个);(d)处理后的相位图中残差点(14个);(e) Goldstein解包裹方法枝切线(1047条);(f)改经后解包裹枝切线(19条)
Figure 4. Examples of removing residual points guided by electromagnetic force. (a) Original phase diagram; (b) Processed phase diagram; (c) Residual points in original phase diagram (885); (d) Residual points in processed phase diagram (14); (e) Branch lines in Goldstein unwrapping branch-cut (1047); (f) Branch lines in improved unwrapping branch-cut (19)
图 7 两种枝切法解包裹对比。(a) Goldstein枝切法求得的枝切线;(b) 改进后枝切法求得的枝切线;(c) Goldstein枝切法解包裹图;(d) 改进后枝切法解包裹图
Figure 7. Comparison of the two branch-cut methods. (a) Branch lines in Goldstein branch-cut method; (b) Branch lines in improved branch-cut method; (c) Unwrapping diagram in Goldstein branch-cut method; (d) Unwrapping diagram in improved branch-cut method
图 9 枝切法解包裹。(a)变形前4幅散斑图;(b)变形后4幅散斑图;(c)原始相位图;(d)滤波后相位图;(e)传统枝切法解包裹图;(g)改进后枝切法解包裹图
Figure 9. Unwrapping by branch-cut method. (a) The four speckle diagrams before deformation; (b) The four speckle diagrams after deformation; (c) Original phase diagram; (d) The phase diagram after filtering; (e) Unwrapping diagram by traditional branch-cut method; (g) Unwrapping diagram by improved branch-cut method
表 1 相位图处理计算总耗时
Table 1. Computing time of phase diagram processing
Operate Parameters Time consuming/ms CPU GPU Phase calculation 5 million pixels 719 148 sin-cos filtering “3×3”,20 times 17571 403 Branch-cut unwrapping 89 residual points 1142 901 -
[1] Wang Yonghong, Lyu Youbin, Gao Xinya, et al. Research progress in shearography and its applications [J]. Chinese Optics, 2017, 10(3): 8-17. (in Chinese) [2] Hu Huiran, Dan Xizuo, Zhao Qihan, et al. Automatic extraction of speckle area in digital image correlation [J]. Chinese Optics, 2019, 12(6): 1129-1137. (in Chinese) [3] Wang Yonghong, Feng Jiaya, Wang Xin, et al. Shearing speckle interferometry based on slit aperture for dynamic measurement [J]. Optics and Precision Engineering, 2015, 23(3): 646-653. (in Chinese) [4] Han Yu, Zhang Qican, Wu Yingshan. Hybrid phase unwrapping algorithm combining branch-cut and surface-fitting for InSAR [J]. Acta Optica Sinia, 2018, 38(8): 0815006. (in Chinese) [5] Han Xu, Wang Lin, Fu Yanjun. Phase unwrapping method based on dual-frequery heterodyne combined with phase encoding [J]. Infrared and Laser Engineering, 2019, 48(9): 0913003. (in Chinese) doi: 10.3788/IRLA201948.0913003 [6] Han Jiang, Yuanping Xu, Chaolong Zhang, et al. An algorithm combining the branch-cut method and rhombus phase unwrapping algorithm [J]. Journal of Physics: Conference Series, 2020, 11(10): 90-98. [7] Sun Yubo, Xiong Lingling, Zhang Pu, et al. Optical design of laser diode beam-homogenizing system [J]. Infrared and Laser Engineering, 2019, 48(12): 1205003. (in Chinese) doi: 10.3788/IRLA201948.1205003 [8] Lu Li, Yi Zheng, Kun Yang, et al. Modified three-wavelength phase unwrapping algorithm for dynamic three-dimensional shape measurement [J]. Optics Communications, 2020, 23(4): 100-106. [9] Wang Jianhua, Yang Yanxi. Branch-cut algorithm with fast search ability for the shortest branch-cuts based on modified GA [J]. Journal of Modern Optics, 2019, 66(5): 473-485. doi: 10.1080/09500340.2018.1548663 [10] Liu Liu Tiandong, Shang Zhengguo, Wu Jiabao, et al. Improved branch-cut phase unwrapping strategy based on dynamic adjacent table [J]. The Journal of Engineering, 2019, 2019(19): 5805-5809. doi: 10.1049/joe.2019.0352 [11] Shao Heng, Zhou Yong, Qi Junfeng, et al. GPU accelerated image processing for electronic speckle pattern shearing interferometry [J]. Chinese Journal of Liquid Crystals and Displays, 2019, 34(10): 1022-1011. (in Chinese) [12] Chen Yu, Pan Yongqiang, Liu Bingcai, et al. Linear phase error suppression technique based on window Fourier transform [J]. Optics and Precision Engineering, 2020, 28(6): 1315-1324. (in Chinese) -







 下载:
下载:


















































