-
激光扫描三维重建作为一种新兴的空间数据获取技术已广泛应用于多种领域[1-2]。采用三维激光扫描仪对特定目标扫描采集点云时,受到目标尺寸、外界环境等因素干扰,致使点云无法被一次性获取,需多站点多角度多次扫描才能实现,多站点云需进行配准,转换到统一坐标系中形成完整点云。
点云配准主要采用Besl[3]提出的传统迭代最近点(Iterative Closest Point, ICP)算法,具有良好配准精度,但收敛速度慢,且当两组点云存在较大差异时,算法会陷入局部最优解,鲁棒性差[4]。为了提高配准效率,在进行ICP配准之前可以先进行粗配准[5]。粗配准是根据局部特征的旋转平移不变性,采用特征匹配实现[6]。如李宇翔[7]提出基于内部形态描述子结合K-D tree的改进迭代最近点配准算法来提高配准速度;Rasu[8]使用点特征直方图对点的几何特征描述得到多维特征向量;孙文潇[9]采用局部表面拟合进行法线估计并计算其快速点特征直方图进行粗配准。
在ICP算法优化中,卢纯青等[10]基于深度信息动态尺度估计方法提升点云配准的时间稳定性和配准精度;Bae[11]计算点与其邻域内点集组成的协方差矩阵,使用点的曲率变化率代替表面曲率,减少计算量;唐志荣[12]使用典型相关分析法对两组转动矩阵进行求解,实现点云配准;黄源[13]根据点云在不同半径内的法向量变化度提取特征点,利用距离约束条件获取准确匹配点;王帅等[14]使用谱聚类按几何结构特征分割各视角点云区域,采用改进ICP精确配准点云。
现有文献对粗配准、精配准ICP算法及其各种变种算法研究集中在优化算法本身上,而对加速搜索算法和错误对应点对配准算法精度和速度的影响研究较少。为进一步提高点云配准算法的速度和精度,笔者所在课题组融合多种优化方法,重点提高搜索速度和特征值提取速度,包括优化点特征直方图提取方法与效率、采样一致性初始配准(Sample Consensus Initial Alignment, SAC-IA)和采用最优节点优先K-D tree近邻搜索法等,来实现高效、高精度的ICP点云优化配准算法。
-
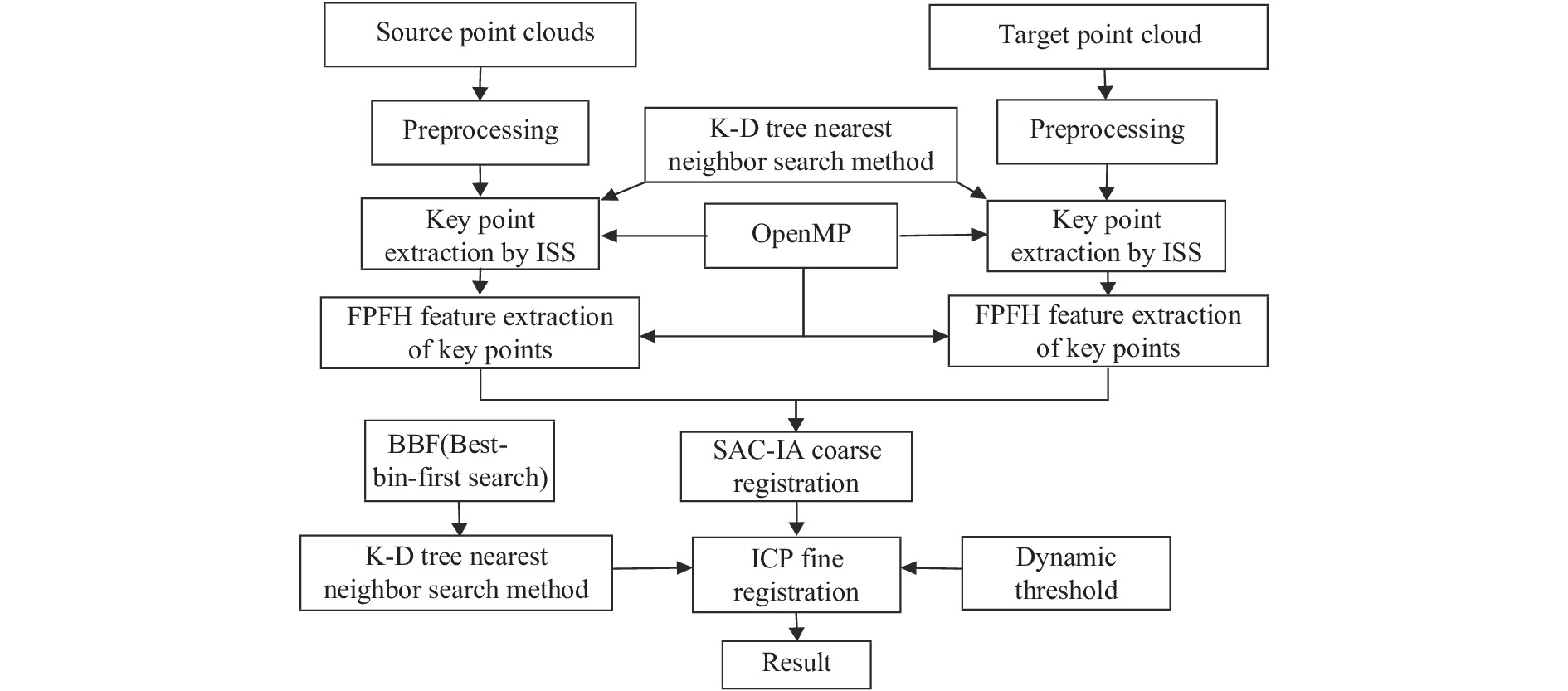
如图1所示为融合了多种优化算法实现点云高效配准的优化方案。其中,在点云预处理中对点云进行体素网格滤波;在关键点选择中,采用内部形态描述子(Intrinsic Shape Signatures, ISS)算法提取关键点;在特征提取优化中,嵌入多核多线程OpenMP并行处理模式,加速关键点快速特征直方图提取;在粗配准中,采用采样一致性初始配准优化;精配准中,采用最优节点优先法优化K-D Tree近邻搜索,加速对应关系点对搜索,同时设置动态阈值剔除错误对应关系点对,提高精匹配精度。
-
由于激光雷达扫描点云中空间点数目非常大,会影响点云的配准效率;另外点密度分布也不均匀,且扫描点存在粗大误差和测量误差,因此有必要进行体素栅格滤波。根据原始点云分布空间创建八叉树三维体素栅格,细分深度8。在每个小网格体素中,用所有点的重心近似代替体素中所有点,可得降采样点云的同时还保持点云基本形状特征。
-
采用内部形态描述子算法进行关键点提取:设点云
$W$ 中含$m$ 个点,${p_i} = \left( {{x_i},{y_i},{{\textit{z}}_i}} \right),i = 1,2, \cdots ,m$ ,对每个点${p_i}$ 建立一个局部坐标系,并设定一搜索半径${r_{iss}}$ ,确定${p_i}$ 为球心、${r_{iss}}$ 为半径球体内的包含点,计算权值${\omega _{ij}}$ :$${\omega _{ij}} = \frac{1}{{\left\| {{p_i} - {p_j}} \right\|}},\left| {{p_i} - {p_j}} \right| < {r_{iss}}$$ (1) 计算每个点
${p_i}$ 的协方差矩阵:$${\rm{cov}} \left( {{p_i}} \right) = \frac{{\displaystyle\sum\limits_{\left| {{p_i}{ - _j}} \right| < {r_{iss}}} {{\omega _{ij}}\left( {{p_i} - {p_j}} \right){{\left( {{p_i} - {p_j}} \right)}^\rm T}} }}{{ \displaystyle\sum\limits_{\left| {{p_i} - {p_j}} \right| < {r_{iss}}} {{\omega _{ij}}} }}$$ (2) 获得协方差矩阵的特征值
$\left\{ {\lambda _i^1,\lambda _i^2,\lambda _i^3} \right\}$ ,从大到小排序;设置阈值${\eta _1}$ 和${\eta _2}$ ,满足$\dfrac{{\lambda _i^2}}{{\lambda _i^1}} \leqslant {\eta _1}$ 和$\dfrac{{\lambda _i^3}}{{\lambda _i^2}} \leqslant {\eta _2}$ 的点即为关键点。 -
如图2所示,基于中心点与
$k$ 邻域之间的法向矢量关系计算点特征描述向量。图2(a)以关键点
${p_q}$ 为中心划半径为$r$ 圆球,包含$k$ 个近邻点。如图2(b)所示,将${p_q}$ 与$k$ 个邻域点拟合为一小平面,其法向量即${\vec n_q}$ ,对${\vec n_q}$ 定义一个笛卡尔坐标系,三坐标轴为:$$\left\{ \begin{array}{l} \vec x = {{\vec n}_q} \\ \vec y = \vec x \times \dfrac{{\overrightarrow {{p_k} - {p_q}} }}{{{{\left\| {{p_k} - {p_q}} \right\|}_2}}} \\ \vec {\textit{z}} = \vec x \times \vec y \\ \end{array} \right.$$ (3) 描述
${\vec n_q}$ 与某近邻点${p_k}$ 法线${\vec n_k}$ 之间的相对空间偏差关系,用三个角度特征值:$$\alpha = \arccos (\vec y \cdot {\vec n_k})$$ (4) $$\varphi = \arccos \left(\vec x \cdot \frac{{\overrightarrow {{p_k} - {p_q}} }}{{{{\left\| {{p_k} - {p_q}} \right\|}_2}}}\right)$$ (5) $$\theta = \arctan \left( {\vec {\textit{z}} \cdot {{\vec n}_k},\vec x \cdot {{\vec n}_k}} \right)$$ (6) 计算出
${p_q}$ 与半径$r$ 邻域内所有点组成的点对之间的三个特征值后,用直方图统计三个特征值的区间分布数目,记为简化点特征直方图 (Simplified Point Feature Histogram,SPFH)。再依次查询每个邻域点${p_{ki}}$ 的SPFH。综合关键点${p_q}$ SPFH特征和$k$ 个近邻点SPFH特征,计算关键点${p_q}$ 的FPFH直方图的特征序列为:$${\rm{FPFH}}\left( {{p_q}} \right) = {\rm{SPFH}}\left( {{p_q}} \right){\rm{ + }}\frac{1}{k}\sum\limits_{i = 1}^k {\frac{1}{{{d_i}}} \cdot {\rm{SPFH}}\left( {{p_i}} \right)} $$ (7) 式中:
${d_i}$ 为对应点对的欧氏距离。FPFH将三个特征
$(\alpha ,\varphi ,\theta )$ 的参数范围均划分为11个统计子区间,统计每个子区间上的点数目,合并得到一个33维特征向量。点的几何位置不同,FPFH值也各有特点。 -
提取FPFH特征向量后,通过采样一致性算法粗配准目标点云和模板点云:(1)模板点云中,获取
$m$ 个待配准特征点;(2)目标点云中,搜索与模板点云中特征点FPFH值相似的所有点,随机选一个相似点作为从模板点云到目标点云的对应关系点;(3)计算对应关系点对的旋转平移矩阵,及对应关系点旋转平移转换后的距离误差总和函数,即Huber损失函数:$${L_h}\left( {{e_i}} \right) = \left\{ \begin{array}{l} \dfrac{1}{2}{\left\| {{e_i}} \right\|^2}, \;\;\;\; \left\| {{e_i}} \right\| \leqslant r \\ \dfrac{1}{2}r\left( {2\left\| {{e_i}} \right\| - r} \right), \;\;\;\; \left\| {{e_i}} \right\| > r \\ \end{array} \right.$$ (8) 式中:
$r$ 为距离阈值;$\left\| {{e_i}} \right\|$ 为对应点对间的欧氏距离。Huber损失函数最小值对应的旋转平移变换矩阵就是粗配准所求的最优变换矩阵。 -
采用最优节点优先 (Best Bin First, BBF)优化K-D Tree近邻搜索,加速对应点对搜索:
(1)分割结点确定,统计所有特征点在(x, y, z)各维度方差,方差最大的维度为主维度,将特征点按主维度排序,正中间特征点为分割结点。
(2)搜索对应关系点对,待查询点值与分割结点值比较,若小于等于,则进左子树,否则进右子树,沿K-D Tree搜索,直至叶子结点,在此子空间内查找与待查询点距离最近点,同时建立优先级,点的优先级
${T_{pri}}$ 定义为:$${T_{pri}} = \left| {{s_i} - {r_i}} \right|,i \in (x,y,z)$$ (9) 式中:
${s_i}$ 为待查询点第$i$ 维值;${r_i}$ 为特征点第$i$ 维值,$i$ 为分割维度。${T_{pri}}$ 越小,优先级越大。(3) “回环”搜索,按优先级大小查找是否存在与该点距离更近的对应点,若在其他分割子空间中存在,则进入此子空间继续搜索。
-
将每次迭代完的配准误差(即欧式适合度评分)设置为下次迭代的距离阈值,进行自适应动态设置,在第
$\omega $ 次配准误差为[15]:$${R_{MS}} = \sqrt {\frac{1}{{n - 1}}{{\sum\limits_{i = 1}^n {\left\| {\left( {{p_{a,i}} - \left( {{R_\omega } \cdot {p_{b,i}} + {t_\omega }} \right)} \right)} \right\|} }^2}} $$ (10) $$\left\| {\left( {{p_{a,i}} - {p_{b,i}}} \right)} \right\| \leqslant \delta $$ (11) 式中:
${R_\omega }$ 和${t_\omega }$ 分别为第$\omega $ 次迭代的旋转和平移矩阵;$\delta $ 为迭代的距离阈值。点云偏差一般服从正态分布,则取$\delta {\rm{ = }}3{R_{MS}}$ ,剔除不满足公式(11)的对应点对,防止该点对参与下次迭代。 -
采用两组点云进行算法验证实验。第一组采用PCL官网下载建筑物点云;第二组为采用激光雷达扫描建筑物获得。实验采用计算机硬件环境:处理器Intel(R) Core(TM) i5-8300H CPU @ 2.30 GHz,内存16.0 GB;操作系统ubuntu 16.04,64-bit,编程语言VC++。
-
图3(a)建筑物点云,目标点云(绿色)共112586个点,模板点云(红色)共112624个点,两原始点云经体素滤波后如图3(b)所示,滤波后分别含17677、17640个点。
从目标点云和模板点云中分别随机选取两个关键点进行特征提取并显示点特征直方图,如图4所示,A、C是模板点云的关键点,B、D是目标点云的关键点。其中,
$A$ 点和$D$ 点的FPFH特征基本一致,因此作为一组对应关系点对。
图 4 关键点FPFH特征值及其比较。(a) A点;(b) B点;(3) C点;(4) D点
Figure 4. FPFH eigenvalues and its comparison of key points. (a) Point A; (2) Point B; (3) Point C ; (4) Point D
当加入ISS算子后,比较了点云的配准效果。如表1所示,其中SAC-IA是进行传统FPFH特征提取进行的配准实验结果,SAC-IA+ISS是先提取ISS关键点、然后再进行FPFH特征提取进行配准的实验结果。表1的结果表明,采用ISS算子提取关键点后,配准欧拉评分近似相同,而配准时间却减少近一半,由12.061 s降为6.797 s,因此ISS算子的引入有效提高了点云的配准效率。
表 1 ISS算子对点云配准影响的比较
Table 1. Comparison of effect of ISS on point clouds registration
Experimental point clouds Algorithms Original points Down-sampling points Euclid score Time/s Building SAC-IA 112586 17677 0.0086 12.061 SAC-IA+ISS 112624 17640 0.0087 6.797 在特征提取过程中,嵌入了OpenMP多核多线程并行计算模式,加快特征提取速度,采用单线程pcl::FPFH Estimation特征提取耗时13.522 s,而采用OpenMP模式耗时3.058 s,仅为单线程的22.6%。基于提取的FPFH特征值进行粗配准,共耗时6.091 s,粗配准的点云效果如图5(a)所示,同时获得了两组点云的粗配准变换矩阵。两组点云基本重合,但仍有较明显错位,需进一步精配准。

图 5 SAC-IA粗配准和ICP精配准后点云效果图
Figure 5. Point cloud results with SAC-IA coarse registration and ICP fine registration respectively
完成粗配准后,再进行优化ICP配准,耗时0.895 s,共迭代5次,欧式适合度评分为0.0040。其中,欧式适合度评分是目标点云到模板点云对应关系点对的距离平方和。ICP精配准效果如图5(b)所示,同时获得了两组点云的精配准变换矩阵。
为比较,对两组点云进行常规ICP配准,共耗时8.297 s,迭代45次,欧式适合度评0.0041。
-
将激光雷达固定在三角支架上,获得不同站点实验室走廊的扫描点云。取两站点扫描的激光点云进行配准,第一组为红色点云,含290545点;第二组为绿色点,含290608点,如图6(a)所示。对两个原始点云进行体素网格滤波后分别含5938、5942个点,如图6(b)所示。

图 6 走廊点云配准实验。(a) 原始点云对;(b) 滤波后点云对;(c) SAC-IA粗配准;(d) ICP精配准
Figure 6. Corridor point clouds registration experiment.(a) Original point clouds pairs; (b) Filtered point clouds pairs; (c) SAC-IA coarse registration; (d) ICP fine registration
对走廊点云筛选关键点,提取FPFH特征,并进行SAC-IA粗配准,求取两组点云的变换矩阵,粗配准效果如图6(c)所示,耗时1.080 s,同时获得了两组点云的粗配准变换矩阵。
对粗配准获得的两组点云再进行优化ICP配准,耗时0.416 s,迭代7次,欧式适合度评分0.0057,如图6(d)所示,同时获得了两组点云的精配准变换矩阵。
为比较,对走廊点云进行常规ICP配准,共耗时2.042 s,迭代33次,欧式适合度评分0.0058。
-
点云配准结果的主要评估标准是迭代次数、欧式适合度评分和配准耗时。上述两个配准验证实验中,常规ICP算法和优化算法的评估参数如表2所示。另外,为了进一步说明所提出的优化组合方式的优越性,与参考文献[8]所采用的点云配准方法进行了实验比较,此方法记作SAC-IA+ICP,即采用采样一致性的粗配准和精配准的组合,实验结果也列入表2中。由表2可见,在欧拉评分近似相同的配准精度效果下,组合优化方法Optimized SAC-IA+ICP在迭代次数和配准时间上均有显著改善。
表 2 三种算法配准评估指标对比
Table 2. Comparison of registration evaluation parameters for three algorithms
Experimental point clouds Algorithms Original points Down-sampling points Iteration number of ICP Euclid score Time/s Building Conventional ICP 112586 17677 45 0.0041 8.297 SAC-IA+ICP 112624 17640 12 0.0041 7.586 Optimized SAC-IA+ICP 5 0.0040 6.986 Corridor Conventional ICP 290545 5938 33 0.0058 2.042 SAC-IA+ICP 290608 5942 14 0.0057 1.566 Optimized SAC-IA+ICP 7 0.0057 1.496 由表2可见,优化的SAC-IA+ICP在两组实验中的迭代次数均远少于常规ICP,仅为其1/9~1/4。另外,优化的SAC-IA+ICP在两组实验中计算速度均快于常规ICP,在第一组实验中,优化的SAC-IA+ICP的计算速度为6.986 s,约占常规ICP的84.19%;在第二组实验中,优化的SAC-IA+ICP的计算速度为1.496 s,约占常规ICP的73.26%。优化SAC-IA+ICP在两组实验中得欧式适合度评分均略优于常规ICP。
-
提出了一种融合多种优化算法的激光点云高效ICP配准方法,采用多核多线程OpenMP模式加快FPFH特征提取,根据提取的点云FPFH特征采用SAC-IA粗配准计算初始旋转平移变换矩阵,采用最优节点优先法优化K-D tree近邻搜索法加速搜索,及设置动态阈值消除错误点对等优化措施。通过对建筑物点云和走廊点云进行算法验证,比较了优化SAC-IA+ICP算法和常规ICP配准算法的性能,结果可知,优化SAC-IA+ICP算法的迭代次数减小为1/9~1/4,耗时减小为73.26%~84.19%,欧式适合度评分有所降低,因此,具有高效和高精度的优势。
Optimization and performance verification of high efficiency ICP registration for laser point clouds
-
摘要: 激光点云常规匹配算法是迭代最近点(Iterative Closest Point, ICP)算法,但其收敛速度慢、鲁棒性差,因此,提出一种融合多种优化算法的激光点云高效ICP配准方法。首先对点云体素滤波降采样,通过ISS算子提取关键点,采用快速点特征直方图(Fast Point Feature Histograms, FPFH)提取关键点特征,嵌入多核多线程并行处理模式 (OpenMP)提高特征提取速度;然后基于提取的FPFH特征,使用采样一致性初始配准算法(Sample Consensus Initial Alignment, SAC-IA)进行相似特征点粗配准,获取点云集间的初始旋转平移变换矩阵;最后采用ICP算法进行精配准,同时采用最优节点优先(Best Bin First, BBF)优化K-D tree近邻搜索法来加速对应关系点对的搜索,并设定动态阈值消除错误对应点对,提高配准快速性和准确性。对两个实例的配准点云进行了实验验证,结果表明,提出的优化配准算法具有明显速度优势和精度优势。Abstract: The conventional Iterative Closest Point(ICP) matching algorithm for laser point clouds had problems of slow convergence and poor robustness, therefore, a point clouds registration method combining multiple optimization methods was proposed. Firstly, point clouds were de-sampled using voxel grid filtering and key points were extracted by ISS operator, then feature extraction algorithm was performed to obtain Fast Point Feature Histograms(FPFH) features of key points, and the multi-core and multi-thread OpenMP parallel processing mode was operated to improve the speed of feature extraction. Then, based on the extracted FPFH features, the Sample Consistency Initial Alignment(SAC-IA) algorithm was used for coarse registration of similar feature points to obtain initial transformation matrix between point clouds sets. Finally, the ICP algorithm was used for fine registration, and the K-D tree nearest neighbor search method optimized by Best Bin First(BBF) was used to accelerate the search speed of corresponding point pairs, and dynamic threshold was set to eliminate the wrong corresponding point pairs, so as to improve the speed and accuracy of point clouds registration. Experimental research on two sets of point clouds shows that the optimized registration algorithm has obvious speed advantages and improves the registration accuracy.
-
表 1 ISS算子对点云配准影响的比较
Table 1. Comparison of effect of ISS on point clouds registration
Experimental point clouds Algorithms Original points Down-sampling points Euclid score Time/s Building SAC-IA 112586 17677 0.0086 12.061 SAC-IA+ISS 112624 17640 0.0087 6.797 表 2 三种算法配准评估指标对比
Table 2. Comparison of registration evaluation parameters for three algorithms
Experimental point clouds Algorithms Original points Down-sampling points Iteration number of ICP Euclid score Time/s Building Conventional ICP 112586 17677 45 0.0041 8.297 SAC-IA+ICP 112624 17640 12 0.0041 7.586 Optimized SAC-IA+ICP 5 0.0040 6.986 Corridor Conventional ICP 290545 5938 33 0.0058 2.042 SAC-IA+ICP 290608 5942 14 0.0057 1.566 Optimized SAC-IA+ICP 7 0.0057 1.496 -
[1] Hu Yanwei, Wang Jianjun, Fan Yuanyuan, et al. LiDAR-based three-dimensional modeling and volume calculation for space objects [J]. Chinese Journal of Lasers, 2020, 47(5): 0510001. (in Chinese) doi: 10.3788/CJL202047.0510001 [2] Wang Jianjun, Xu Lijun, Fan Yuanyuan, et al. A method for compensating platform attitude fluctuation for helicopter-borne LiDAR: Performance and effectiveness [J]. Measurement, 2018, 125(9): 37-47. [3] Besl P J, McKay N D. A method for registration of 3-D shapes [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239-256. doi: https://doi.org/10.1109/34.121791 [4] Sun Junhua, Xie Ping, Liu Zhen, et al. Automatic 3D point cloud registration based on hierarchical block global search [J]. Optics and Precision Engineering, 2013, 21(1): 174-180. (in Chinese) doi: 10.3788/OPE.20132101.0174 [5] Wang Bin, Liu Lin, Hou Yuqing, et al. Three-dimensional cardiac point cloud registration by improved iterative closest point method [J]. Optics and Precision Engineering, 2020, 28(2): 474-484. (in Chinese) [6] Zong Wenpeng, Li Guangyun, Li Minglei, et al. A survey of laser scan matching methods [J]. Chinese Optics, 2018, 11(6): 914-930. (in Chinese) doi: 10.3788/co.20181106.0914 [7] Li Yuxiang, Guo Jiming, Pan Shangyi, et al. A point cloud registration algorithm based on ISS-SHOT features [J]. Bulletin of Surveying and Mapping, 2020, 0(4): 21-26. (in Chinese) [8] Rusu R B, Blodow N, Beetz M. Fast Point Feature Histograms (FPFH) for 3D registration[C]//IEEE International Conference on Robotics & Automation. IEEE, 2009: 3212-3217. [9] Sun Wenxiao, Wang Jian, Liang Zhouyan, et al. Accurate registration of laser point cloud based on normal feature constraint [J]. Geomatics and Information Science of Wuhan University, 2020, 45(7): 988-995. (in Chinese) [10] Lu Chunqing, Yang Mengfei, Wu Yanpeng, et al. Research on pose measurement and ground object recognition technology based on C-TOF imaging [J]. Infrared and Laser Engineering, 2020, 49(1): 0113005. (in Chinese) doi: 10.3788/IRLA202049.0113005 [11] Bae K H, Lichti D D. A method for automated registration of unorganised point clouds [J]. ISPRS Journal of Photogrammetry & Remote Sensing, 2008, 63(1): 36-54. [12] Tang Zhirong, Liu Mingzhe, Jiang Yue, et al. Point cloud registration algorithm based on canonical correlation analysis [J]. Chinese Journal of Lasers, 2019, 46(4): 0404006. (in Chinese) doi: 10.3788/CJL201946.0404006 [13] Ma Guoqing, Liu Li, Yu Zhenglin, et al. Application and development of three-dimensional profile measurement for large and complex surface [J]. Chinese Optics, 2019, 12(2): 214-228. (in Chinese) doi: 10.3788/co.20191202.0214 [14] Wang Shuai, Sun Huayan, Guo Huichao. Overlapping region extraction method for laser point clouds registration [J]. Infrared and Laser Engineering, 2017, 46(S1): S126002. (in Chinese) doi: 10.3788/IRLA201746.S126002 [15] Guo Yan, Zhou Huilin, Wang Jinwei, et al. An improved distance threshold constrainted ICP algorithm for 3D registration [J]. Journal of China Academy of Electronics and Information Technology, 2011, 6(6): 643-647. (in Chinese) -







 下载:
下载: