下载:
-
图像作为一种方便存储、传输，可视化度高的信息载体，已经成为人类生活中不可或缺的一部分。目前获取图像的主要手段之一是成像。在一般的成像过程中，由光学成像系统汇聚目标场景的光线到多像素的感光元件阵列上，感光元件阵列记录的光强空间分布便是目标场景的像。随着半导体工艺的不断发展，广泛应用在数码相机上的感光元件阵列电耦合器件（Charge Coupled Device, CCD）和互补金属氧化物半导体（Complementary Metal-Oxide Semiconductor，CMOS）已经能够直接捕获亿级像素数的图像。然而，一些研究人员另辟蹊径，研究用只有单一像素的感光元件进行成像，也就是单像素成像（Single-pixel imaging, SPI）。随着研究的不断深入，单像素成像在许多领域拥有巨大的应用潜力已经得到了验证，比如在特殊波段，如X射线成像[1-3]，荧光成像[4, 5]，红外气体检测[6-8]，太赫兹成像[9, 10]。在超快成像[11-13]，超光谱成像[14-18]，遥感追踪[19-22]，光学加密[23-26]，三维成像技术[27-31]等领域，也有着广阔的应用场景。
单像素成像的起源，最早可以追溯到100多年前的逐点扫描成像[32-34]，由于当时面阵探测器的研究还未成熟，这项技术成为获得物体二维图像的主要方式之一。单像素成像发展到现在，已经演变成一种以计算为主的成像方式。目前主流的单像素成像大致被分为两类：一类是受量子成像启发并发展而来的基于关联算法的单像素成像；另一个是依托压缩感知算法产生的单像素相机。
基于关联算法的单像素成像，又称为“鬼成像”（Ghost Imaging）。它通过两条光路的光场的关联运算来重构目标的二维强度信息。其中的一条光路被称为探测光路，其经过目标空间与目标相互作用，然后由单像素探测器探测来自目标区域的透射或反射光光强；另一路则是参考光路，具有与探测光路相同的空间分布，但不与目标产生相互作用，由面阵探测器直接记录其光强空间分布。根据实验中光源和光路的不同，鬼成像先后经历了量子鬼成像、经典鬼成像、计算鬼成像的过程。在1995年，科学家首次在实验上实现了鬼成像[35]。由于在实验中用到的光源是自发参量下转换产生的纠缠光子对，这使得人们认为鬼成像本质上是一种量子现象。由于目标仅存在于单像素探测器所在的物光路，具备空间分辨能力的参考光路无法采集到目标物体的相关信息，单凭任意一条光路都无法重构物体的空间信息。最终，目标的二维图像是通过光场的二阶关联运算得到，研究人员将这一现象命名为量子鬼成像。2004年，科学家用激光器照射毛玻璃后产生的赝热光源也成功地实现了鬼成像实验，证明了量子领域中的光子纠缠在鬼成像实验中不是必须的，打破了鬼成像是一种量子现象的推论[36]。随着对鬼成像研究的不断深入，在2008年一个简化版的用经典光源的计算鬼成像被提出[37]。通过利用空间光调制器来产生已知空间强度分布的光场，如此一来省去了原本两束光路中的参考光路，使得鬼成像在实验中只需要一路探测光路和一个单像素探测器。计算鬼成像的提出让实验装置更为简单，并且避免了参考光路产生的噪声影响，为这项技术走向实际应用迈出了重要一步。
单像素相机最早出现在计算摄像领域，相比于单像素关联成像来说要晚一些。2006年，Donoh等人于提出了压缩感知理论[38-40]，其借助图像的稀疏性信息，可以实现在远低于奈奎斯特采样定律要求的情况下，从随机测量信号中，重构出测量图像。随后，Rice大学就基于压缩感知理论完成了单像素相机成像实验[41]。其利用了一个数字微镜设备（Digital Micro-mirror device, DMD）对物体的像进行二值随机调制，调制后的像由一个单像素探测器探测总的能量。在重构过程中，哈尔小波基被作为稀疏采样基实现图像的稀疏变换，使得系统可以在欠定的采样数据中恢复出清晰的重构图像。此后，又有大量有关单像素相机在重构算法和重构质量上优化的工作被报道[42-50]。单像素相机的提出又进一步丰富了人们对单像素成像的认识，促进了单像素成像理论的健全，丰富了单像素成像的应用空间。虽然单像素关联成像和单像素相机分别出现在不同的研究领域，但随着各自不断的发展，科学家们意识到这两者本质上是一致的，并将两者统称为单像素成像。
另外，单像素成像不仅仅能够像普通数码相机一样得到目标的二维图像，更可以通过结合一些额外的手段来获得高质量的三维信息。2013年，英国格拉斯哥大学的Sun等人在单像素关联成像的实验中加入了四个不同位置的探测器。根据亥姆霍兹互易定律分别得到不同视角下的目标二维图像。利用不同视角下的二维图像和SFS（Shape from shading）技术恢复出目标的三维信息[51]。2016年，格拉斯哥大学的Sun等人又在单像素关联成像的基础上，借助飞行时间切片和压缩感知算法，实现了超单像素探测器精度的高质量三维成像[52]。同年，暨南大学的Zhang等人利用傅里叶变换基的投影和频谱编码以及滤波理论的压缩采样技术和光栅，实现了极少采样数下的单像素三维成像[53]。文中主要对单像素成像技术及其在三维成像中的应用进行了讨论。
-
单像素成像使用不具备空间信息分辨能力的单像素探测器（又有称为“桶探测器”），通过具有一定空间分布的结构光照明，对待成像物体进行空间强度信息采样，结构光经物体调制后的光强信息，会被桶探测器收集，经过多次的迭代采样，获得不同结构光照明情况下的强度信号序列，借由关联算法，实现物体的空间振幅信息实现重构。其基本原理如图1表示。
对于使用旋转毛玻璃进行光场调制的传统单像素成像系统，光源出射后，照射至旋转毛玻璃上，经调制后在固定距离d处产生类似于散斑图的具有一定空间分布的照明图案，经分束器后，一路照射至待成像物体上，经物体调制后的照明图案被单像素探测器收集总强度，另一路散斑图被相机采集。此过程如公式（1）所示：
$$s\left( i \right) = \mathop \sum \nolimits_{x,y = 1}^{M,N} {I_i}\left( {x,y} \right) \times T\left( {x,y} \right)$$ (1) 式中：
$s\left( i \right)$ 为探测器收集的光强值；${I_i}\left( {x,y} \right)$ 为CCD收集到的当前强度图；$T\left( {x,y} \right)$ 为物体的透过率函数。将每次收集到的强度值与对应的照明图案带入关联算法进行运算，即可重构物体的空间二维强度信息，如公式（2）所示：$$\hat T\left( {x,y} \right) = \left\langle {\left[ {s\left( i \right) - \left\langle {s\left( i \right)} \right\rangle } \right] \times {I_i}\left( {x,y} \right)} \right\rangle $$ (2) 式中：
$\hat T\left( {x,y} \right)$ 表示重构的物体二维强度图。借助于空间光调制器件，如液晶空间光调制器和数字微镜阵列，可以将装备相机一端的参考光路省略，从而实现计算式单像素成像系统。相比较于传统的单像素成像系统，计算式单像素成像系统由于省略了参考光路，不仅简化了设备，而且避免了参考光路噪声，使得成像的重构质量大大提升。同时，使用空间光调制设备进行的计算式单像素成像，可以使用预先定制的采样强度图，如阿达玛矩阵、傅立叶矩阵等正交矩阵，可以使得成像所需的采样矩阵数量大大减少，并且进一步提升重构图像的质量。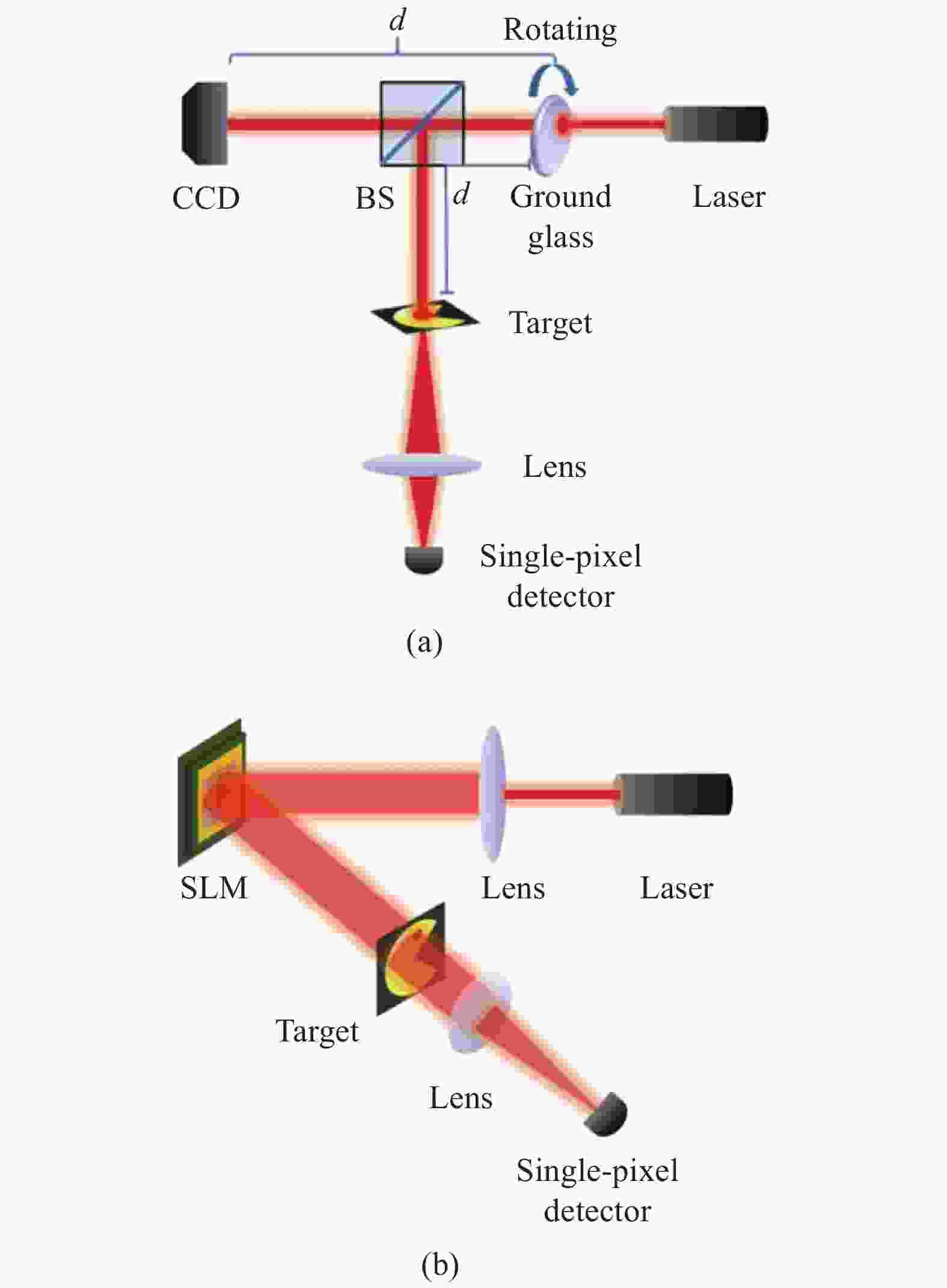
图 1 单像素成像原理图。(a)使用旋转毛玻璃的传统单像素成像；(b)计算单像素成像原理图
Figure 1. Diagram of single-pixel imaging. (a) Traditional single-pixel imaging using rotating ground glass; (b) Computational single-pixel imaging
基于关联算法的单像素成像，在探测端不关注物体的空间信息分布，只收集经物体调制后返回的结构光强度图的总强度信息，即探测强度值，不需要在探测端满足成像公式的要求，极大地降低了光学系统镜头设计的压力。另外，由上述公式理论可以看出，使用关联算法的单像素成像过程，采样与重构家过程彼此独立，由于重构部分完全依赖于计算设备进行运算，与采样端光学设备无关，故两个部分可以顺序操作或异步操作，即采样与重构可以独立运行。采样过程完成后，重构过程可以即刻运行以完成重构，也可以先将所需数据保存，在其他任意时刻进行离线恢复。相比于传统光学成像技术的“所见即所得”，离线操作能力是计算成像技术的一大亮点。
使用关联算法的单像素成像，是依赖于参与采样的结构光场的空间分布与待成像目标的空间分布之间的相关程度，或者说两者的相似度。相似程度越高的采样结构光场分布，所反馈的有效信息像素点就越多，从而被探测器收集到的强度值就越大。探测器得到的探测值经过零均值化后，在重构过程中作为相对加权值作用于对应的结构光采样图。此过程可以将其理解为对应的采样强度图在全部的采样图序列中的可信度，此可信度与该采样强度图同目标物体的相似度成正比。
对于单像素成像物理过程的理解，可以通过亥姆霍兹互易律来进一步解释。对于线性成像系统，可以将输入与输出，即光源位置与单像素探测器位置进行互换，装置对应变换如图2所示。可以发现，变换后的光路与之前的不同点只在于是先进行光场调制还是先照明物体，如果忽略传播过程中的噪声影响，依据之前的公式推导，两者基本没有区别。若将图中SLM、透镜和单像素探测器综合为一个整体，如图中虚线框所示，其作用等效为一个具有空间分辨能力的多像素面阵探测器。此时，单像素成像系统等效为传统的面阵探测器光学成像系统。此时，虚线框内的系统即为典型的单像素相机系统。
若是考虑探测器噪声的影响，在光源照明一定的情况下，由于单像素成像需要多次采样叠加，从而实现了对探测器噪声的平均化作用[54]，其成像质量要优于使用CCD的情况。典型的计算式单像素成像的原理图以及对应的实验重构图像如图3所示。
由于影响单像素成像的主要噪声可分为探测器噪声和光源波动噪声，对两种噪声的抑制能力将极大地决定单像素成像的重构质量。科学家们尝试了多种方式来提升单像素成像系统对噪声的抑制能力，其中最为有效的是差分测量单像素成像技术。差分测量单像素成像技术中最具代表性的工作有差分计算鬼成像（Differential Computational Ghost Imaging, DCGI）和归一化鬼成像（Normalized Ghost Imaging, NGI）。其装置原理图如图4所示。
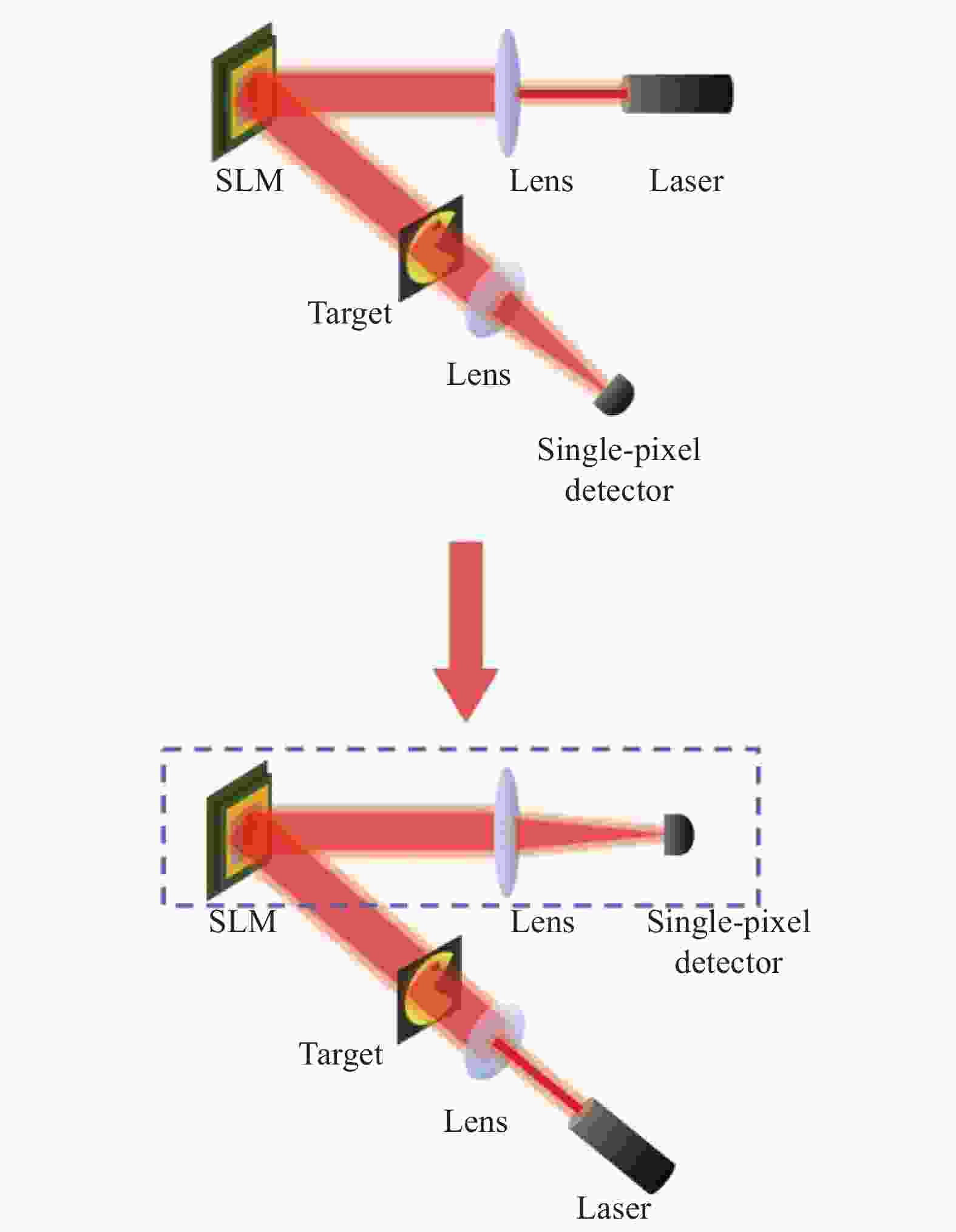
图 2 调换探测器和光源位置后的光路原理图
Figure 2. Diagrams of optical path after exchanging position of detector and light source
图 3 单像素成像典型装置图及其成像结果。其中重构图片的分辨率均为128 pixel×128 pixel
Figure 3. Classical setup of single-pixel imaging and resulting images. All images are reconstructed with a resolution of 128 pixel×128 pixel
归一化鬼成像[55]通过引入一个额外的单像素探测器收集参考光路的结构光场的强度值，将信号光路得到的探测值序列的均值与此参考光路的探测值序列的均值相除得到新的权重值。其重构过程如公式（3）所示：
$$\hat T\left( {x,y} \right) = \left\langle {\left[ {\frac{{s\left( i \right)}}{{r\left( i \right)}} - \frac{{\left\langle {s\left( i \right)} \right\rangle }}{{\left\langle {r\left( i \right)} \right\rangle }}} \right] \times {I_i}\left( {x,y} \right)} \right\rangle $$ (3) 式中：
$r\left( i \right)$ 表示参考光路额外引入的探测器采集得到的当前采样强度图对应的总强度值。由于考虑到了光源波动以及采样矩阵自身空间分布所产生的强度变化的影响，在运算过程中将此影响从探测值中消除，从而实现了单像素成像的重构质量的明显提升。若考虑使用正交采样矩阵的计算式单像素成像系统，则可以进一步优化。差分计算单像素成像的工作应运而生[56]。当使用阿达玛矩阵作为采样强度图时，由于阿达玛矩阵是取值只有±1的二值矩阵，可以通过使用数字微镜阵列投影两张完全相反的阿达玛采样矩阵来实现±1的强度调制。同时，将两次投影的探测值做相减运算，即可以得到差分后的探测值，从而实现对光源强度波动噪声的抑制，同时也可以实现对探测器噪声的抑制。
图 4 归一化鬼成像原理图
Figure 4. Diagram of normalized ghost imaging
单像素成像技术需要多次采样来重构目标物体的二维强度图，从而使得其重构时间相比较于单次曝光的空间复用多像素阵列采样较慢。这也是其难以运用至高速运动物体成像领域的原因之一。随着压缩感知技术的出现，其数学上同单像素成像技术的具有高度的契合性，因此被科学家选择用于优化单像素成像的采样速度[57-60]。通过引入压缩感知技术，考虑待成像物体空间上的稀疏性，大大减少采样所需的结构光强度图的数量，从而实现了成像时间的缩减，使得单像素成像技术具有了对高速运动物体成像的潜力。
-
单像素成像依靠于空间结构光采样，在探测器一端对空间信息具有极低的要求，此特点使得其在特殊波段成像方面具有先天的优势。由于在近红外波段、太赫兹波段以及紫外等波段，阵列探测器的价格远高于单像素探测器，甚至在部分波段还未有对应的阵列探测器。由于考虑实际工业应用中，对成本的控制也是极为重要的因素，同时，考虑到面阵探测器在这些特殊波段中的成像质量较差，成像空间分辨率也受到极大的限制，而逐点扫描技术对于时间成本的要求过高，无法实现较为快速的图像重构，基于关联算法的单像素成像技术就成为了一种更加的选择。
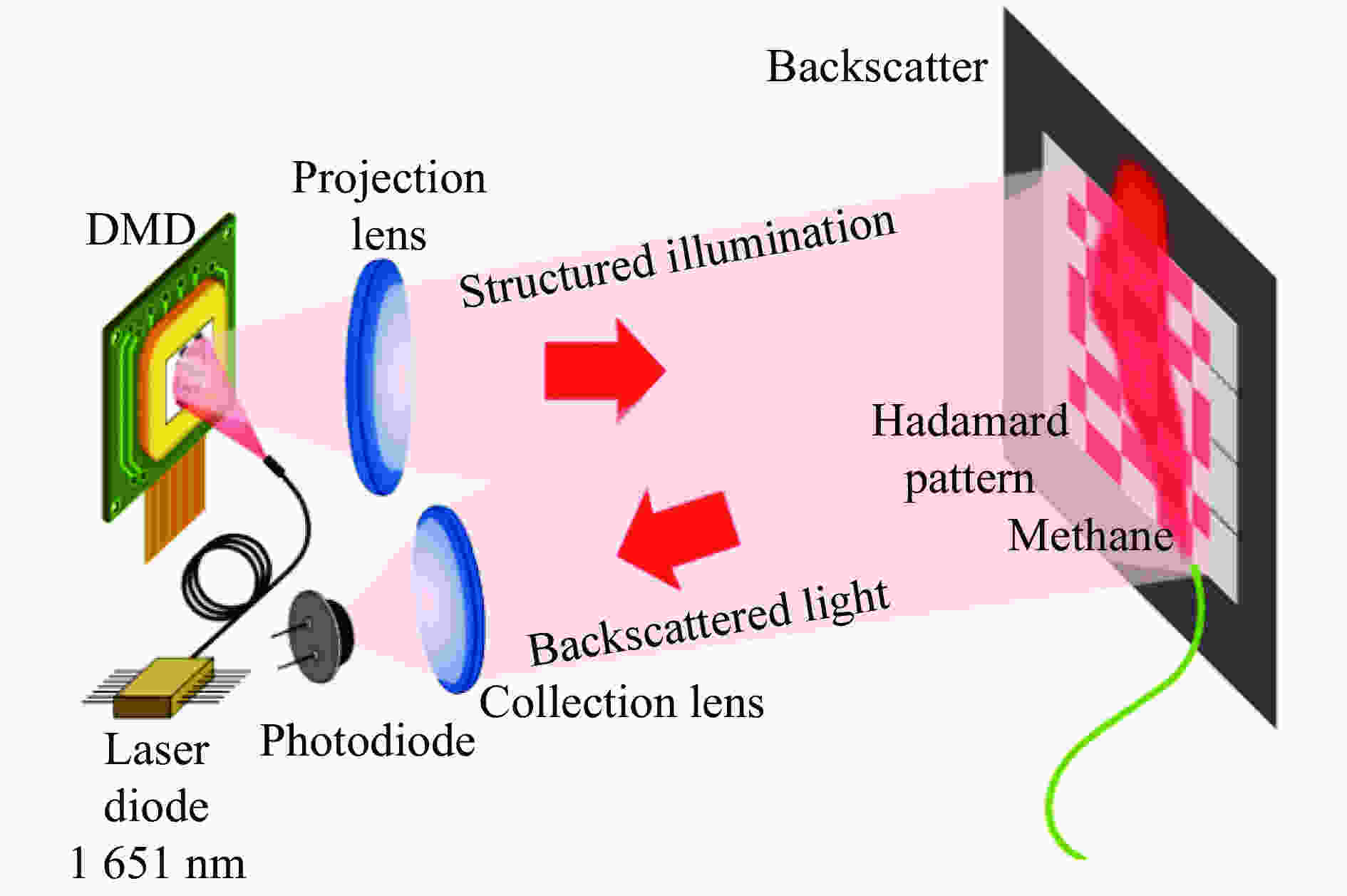
近年来，出现了许多使用特殊波段照明下的单像素成像技术。近红外光源由于其特殊的吸收峰以及较强的穿透能力，近年来广泛引起了研究人员的关注，使用近红外光源的成像和分析技术层出不穷[61-68]。格拉斯哥大学的科学家提出了对甲烷气体进行实时成像的单像素成像技术[69]，其原理图如图5所示。
图 5 对甲烷气体的红外单像素成像原理图
Figure 5. Schematic diagram of infrared single-pixel imaging of methane gas
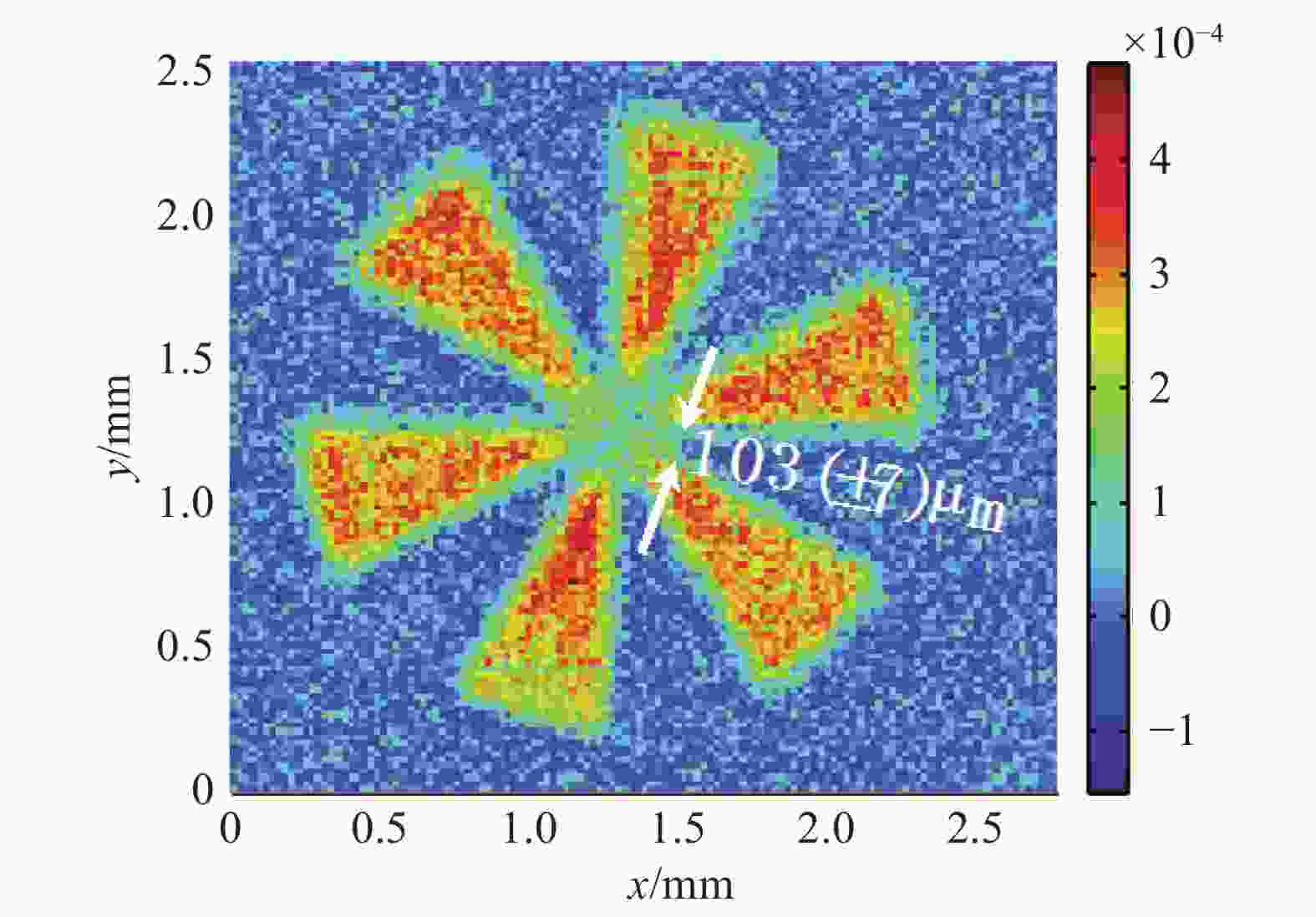
实验采用1651 nm的近红外光源照明数字微镜阵列，使用阿达玛矩阵作为采样结构光矩阵，对甲烷气体进行了实时动态单像素成像。由于甲烷气体的空间信息复杂度较低，所以成像的空间分辨率为16 pixel ×16 pixel，考虑差分测量，所需要的阿达玛矩阵仅有512幅，借助于数字微镜阵列22 kHz的高速刷新率，使得成像的帧率得到了保障。同时，引入一个额外的常规波段下的CMOS相机，用于拍摄成像的实际场景，并且将近红外单像素成像的结果与相机所拍摄的场景结果相结合，实现了在常规场景下甲烷气体位置的实时重构，实验结果如图6所示。
图 6 甲烷气体的红外单像素成像结果
Figure 6. Result of infrared single-pixel imaging of methane gas
此工作的提出，对单像素成像的近红外应用具有高度的参考意义。将传统的可见光成像与特殊波段的单像素成像技术相结合，在需要较高空间分辨率的可见光场景拍摄中使用面阵探测器，成本较低，并且可以进行快速实时成像，而在对于特殊气体进行拍摄中，由于对于空间分辨率具有较低的要求，使用对应波段的单像素成像技术，既可以控制整体成像系统保持较低的成本，又可以避免单像素成像技术成像时间较长的劣势。此工作为甲烷气体等特殊气体的实时监控、探测提供了一种高质量低成本的选择。
对于某些波段，由于材料的限制，很难以制作出高成像质量的面阵探测器，比如太赫兹波段。近年来，太赫兹波段由于其高穿透性等特点，在安防领域，监控领域具有极高的应用价值[70-75]。埃克塞特大学与格拉斯哥大学合作提出的非入侵式太赫兹波段的单像素成像技术，为太赫兹波段成像提供了新的实现方法[76]。实验采用400 m波长的太赫兹波段进行辐射照明，采用800 nm波长100 fs泵浦脉冲照明数字微镜阵列，实现二值采样强度图的投影，通过照明硅半导体薄片来实现太赫兹波段的照明转化，从而对待成像物体进行单像素成像。实验结果如图7所示。
实验选择电路板作为待成像物体进行了成像，同时，对不同压缩比的成像结果进行了比较分析，并通过与传统的逐点扫描技术进行比较，从结果上证明了太赫兹波段下，单像素成像技术无疑是更好的选择。实验首先对比了使用逐点扫描技术进行重构的结果图与使用随机矩阵作为采样矩阵的单像素成像结果图以及使用阿达玛矩阵作为采样矩阵的结果图之间的差异，可以发现使用阿达玛矩阵的单像素成像结果质量最佳，使用随机矩阵的单像素成像结果较差，但仍旧能分辨出重构物体的空间信息，而使用逐点扫描的重构图则基本不能分辩物体的有效信息。
图 7 太赫兹波段单像素成像结果
Figure 7. Single-pixel imaging result at terahertz waveband
同时，考虑使用压缩感知技术，对25%压缩率和75%压缩率的重构图进行对比分析，发现即使使用25%的采样矩阵的情况下，相比较于逐点扫描，单像素成像重构的图像仍旧具有较高的识别度，在75%采样矩阵使用的情况下，其重构质量更是与使用正交阿达玛矩阵的重构结果具有较小的差距。
在紫外以及X射线领域，单像素成像技术由于其高信噪比以及低成本的优势，也引起了研究人员的广泛关注，利用短波段光源的单像素成像技术也相继被提出[77-80]。在可以预见的将来，单像素成像技术将会进一步被优化，成为计算成像领域中不可或缺的重要技术。
-
三维成像技术可以在获取二维图像的同时，得到物体的表面深度信息。在物体的精度测量，表面缺陷分析，三维立体重构和显示等方面有着重要的科研前景和应用价值。而三维单像素成像技术，由于其相对较低的成本和高抗干扰能力在特殊波段以及特殊复杂场景下的测量领域也受到了广泛地关注。
前文已经详细介绍了单像素成像技术的发展历史以及其在二维成像方面高质量和高采样效率的能力，因此，在此基础上发展出了多种单像素三维成像方法。其中，基于强度信息的三维成像，基于条纹的三维成像以及基于扫描的红外成像方式，是当前单像素三维成像研究领域应用最为广泛的实验方向。下文从这三个方面介绍了目前该领域的研究方法和现状。
-
传统的三维成像方法主要采用多视角拍摄的立体视觉方法，使用多个相机在不同视角探测，根据三角成像关系提取出物体的三维信息。这种成像方式要求多个探测器具有严格的像素对应关系，这个条件导致该系统设计难度大，实用性低。与之不同的是，光度立体视觉使用一个固定视角的探测器获取不同方向入射光源照射物体的强度图，从多幅图像中提取出物体的深度信息和表面法向量[81-85]，这种方案中，像素匹配更为容易，技术难度大大降低。
与之类似，基于图像光影分布恢复物体三维形貌也是一种应用广泛且经典的方法。在传统的阴影重构物体面型的方法中，对于同一个探测器和光源的光照强度相同前提下，目标物体的成像亮度将由物体的表面反射率来决定，而物体的表面反射率将主要受到物体表面材质和物体表面的几何形状决定。由此，基于阴影重构物体面型的方法可以通过探测得到的二维图像中物体的亮度信息，在上文介绍的条件假设下，可以求得空间中物体表面的法向量，进一步根据法向量的分布可以获取面型变化梯度，从而得出所求物体的三维面型。由此可知，将物体阴影信息的提取并转换到目标物体的深度信息是该技术的核心。
图8展示出了基于阴影重构物体面型的三维单像素实验装置，基于红绿蓝三基色的数字投影仪投影出由计算机生成的0/1随机亮暗图案，经物体面型调制后反射的光场由四个均匀分布在投影仪上下左右四个方位的单像素探测器探测，由于物体面型的变化不同视角下的探测器将得到不同的探测值，从而重构物体在不同视角下的二维图像。
图 8 基于多个单像素探测器的三维成像原理图
Figure 8. Schematic diagram of 3D imaging based on multiple single-pixel detectors
在经典的成像系统中，物体表面的阴影分布将完全受到光源的影响，相机在不同的探测角度将会得到完全相同的阴影分布。对于在单像素成像系统，单像素探测器完全不具备空间分辨能力，而光源端的投影仪将唯一性地决定重构物体的分辨率。根据成像系统的互逆性原理，单像素探测器的分布方位将决定重构物体的阴影分布。在图9中，可以明显地看出不同视角下探测器重构得到的二维图像有不同明暗分布。
图 9 不同视角下单像素探测器获得的重构图
Figure 9. Reconstructions of single-pixel detectors at differet points of view
在假设目标物体反射率相同的前提下，根据不同探测器重构图案的亮度值，可以得到不同像素点的表面法向量，而根据这些表面法向量可以进一步求得相邻像素点之间的梯度分布，从物体表面一个给定点开始积分计算可以初步获得物体的深度变化，在经过后续的优化步骤之后可以达到经典光度立体视觉的三维重构效果如图10所示。
图 10 整合面法线数据，叠加反射率数据后得到的重构面视图
Figure 10. Reconstructions after integrating the normal vectors and superimposing the reflectivity data
受上述方法的启发，格拉斯哥大学的Zhang[86]等在随后提出了基于该方法的三维单像素视频成像的方法，在该实验中使用了一种被称为进化压缩感知的单像素压缩方法。在使用阿达玛矩阵进行单像素成像过程中，相邻投影图之间的探测信号强度几乎是相同的。因此，基于探测到的平均信号强度对投影图案进行排序，并将排序靠前的矩阵生成二维投影图。这种压缩方式中，对于每一个新图案随机地从剩余阿达玛矩阵中选择一部分替代在高排名图案中排名靠后的一部分。基于这种进化式压缩感知方法，在做到高帧速率投影的同时较大程度地保留空间分辨率。
该实验中，具有压缩比为12.5%的128 pixel×128 pixel的单像素二维强度图仍能重构出效果较为明显128 pixel×128 pixel分辨率的1 Hz三维重构视频也在文中做了展示，成像物体为旋转的石膏人头骷髅。需要注意的是，在该速率下的三维重构过程中的三维结果图，除此之外，具有25%压缩比，探测器速率以及单像素重构二维图像时间都不再是成像速率的瓶颈，三维重构算法使用时间成为了限制成像速度的主要因素。
-
傅里叶单像素三维成像技术是基于二维傅里叶单像素成像技术，并根据条纹投影轮廓术[6]提取物体深度信息的三维成像方法。
二维的傅里叶单像素成像是使用具有不同空间频率的傅里叶基底作为空间光调制器的投影图案，经物体的后向反射光由单像素探测器收集，将光强探测值与投影图案进行关联运算，并经过逆傅里叶变换之后可以得到物体的重建图像[87]。
傅里叶单像素三维成像系统实验装置如图11所示，投影系统作为空间光调制器投影出电脑产生的傅里叶投影条纹，投影到物体表面上的图案经过成像透镜后成像在光栅面上，经过收集透镜后由单像素探测器进行探测。
需要提到的是，传统的条纹投影轮廓术[88]中，在光源端投影出光栅条纹到物体表面，物体面型将会对条纹相位进行调制，经过探测系统采集到变形后的条纹图，从中可以提取出条纹图的相位变化从而重构出物体形貌。与传统的探测系统相比，该系统满足亥姆霍兹互易性[89]，因此，如图11中所示将物体后向发射的光场进行条纹调制同样可以实现条纹投影轮廓术的成像方法。
傅里叶单像素三维成像技术的重构过程如图12所示，目标为图12(a)中的白色纸浆葫芦经过光栅后的畸变条纹图，在重构物体面型的过程中，首先使用傅里叶条纹相位提取算法提取出目标物体的傅里叶频率里的一级频谱部分，如图12(b)所示。并进一步从一级频谱中提取出条纹调制的相位分布，最终通过该分布映射到实际三维立体中的深度尺寸。
图 11 傅里叶单像素三维成像系统实验简图
Figure 11. Diagram of 3D Fourier single-pixel imaging system
图 12 傅里叶单像素三维成像系统实验结果
Figure 12. Experimental results of Fourier 3D single-pixel imaging
在自然图片空间域中，大部分能量会集中在傅里叶频域的低频部分，也就是说频域中的自然图像具有足够的稀疏性。傅里叶单像素成像方法可以根据这种稀疏特性，有选择地投影不同频率的傅里叶图案，从而能够在保留大多数图像信息的同时有效地减少测量次数，从而提高测量效率。Zhang组实验中重建了图像分辨率为599 pixel×599 pixel，压缩比为5.78%的三维形貌图像重构[90]。
除此之外，Zhang等在后续的工作中提出了一种信息多路复用的成像方法。该技术中基于傅里叶频域移频的基本原理，调制和压缩了被探测对象信息并使用单像素探测器进行探测，做到同时恢复目标物体的空间，光谱和三维信息。此外，实验还演示了在88%的压缩率下生成高质量全彩色3D图像的内容。
-
由于数字相移技术具有较高的精度和适用性，该方法是光学立体测量中的最常用方法。其中，数字光栅快速的切换能力，帮助数字正弦条纹投影技术广泛应用于三维成像测量中。
传统的相移成像技术中，相移步数越多得到的相位精度将越高，但相移步数的增加又会致使成像时间成本增加，导致该技术难以应用到快速三维成像。在此系统中采用的四步相移技术，能够在具有相对较高精度的前提下保持一定速度。四步相移算法中每一步相移距离为π/2，相移条纹强度分布可以写作：
$${I_n}\left( {x,y} \right) = I'\left( {x,y} \right) + I''\left( {x,y} \right)\cos \left( {\phi + \frac{{2\pi n}}{4}} \right)$$ (4) 式中：n = 1, … 4；
$I'\left( {x,y} \right)$ 是平均光强；$I''\left( {x,y} \right)$ 是调制强度，而$\phi $ 则是我们希望得到的相位，相位可以通过公式（5）获得：$$\phi \left( {x,y} \right) = {\rm{arctan}}\frac{{{I_1}\left( {x,y} \right) - {I_3}\left( {x,y} \right)}}{{{I_4}\left( {x,y} \right) - {I_2}\left( {x,y} \right)}}$$ (5) 通过上面的技术可以得到一个在
$\left[ { - \pi ,\pi } \right)$ 之间具有$2\pi $ 相位跳变的包裹相位。经过空间相位解包算法后，可以得到物体的绝对相位分布。基于数字光栅的单像素三维成像系统装置图如图13所示，LED面阵光源发出白光经反射镜反射后入射到数字光栅靶面上，然后数字光栅投影正弦光栅条纹经过镜头照射到物体上，正弦条纹经过物体高度面型调制后，反射的光强经过镜头将成像在另一个数字微镜阵列器件靶面上，该微镜器件将会对探测信号再次进行调制，最终使用单像素探测器获得调制后的条纹强度图。数字光栅进行四次相移投影，单像素探测系统可以得到四幅相移条纹图，经过上文提到的相移成像方法中相位提取方法可以从中得到物体相位。
图 13 单像素数字光栅三维成像系统图
Figure 13. 3D single-pixel imaging system based on digital grating
需要说明的是，在该系统中数字光栅采用数字抖动加离焦的方式来投影正弦条纹，抖动产生正弦条纹是通过控制二值条纹中黑白亮点的比例值来实现正弦条纹中灰度分级的效果，相对于直接二值投影，可以消除掉相位中的剧烈变化，减少误差；相对于正弦条纹投影，有具有较快的速度优势，在该系统中，作为数字光栅的DLP6500器件最快能够以9225 Hz的速度切换二值投影图案，因此理论上使用该数字光栅，即使是四步相移也可以实现千赫兹以上的条纹图获取速度。
图14展示了一组使用该系统重构出的三维物体。成像物体为使用3D打印的三棱柱型物体如图14(a)中所示，因打印表面不够光滑，在物体表面覆盖一层素描纸，图14(b)为四步相移实验过程中其中一步相移条纹图，图中明显可以看出物体面型对条纹进行了调制。图14(c)为三维重构出的物体，不同颜色代表深度信息变化情况。
该实验还就相位信息进行了标定。通过使用一块放置于Z轴方向的一维位移平台上的白色平板进行位置移动，在探测位置前后以4 mm为步进值各移动四次，共可以获得九副不同深度的条纹相位信息，通过将相位与深度值进行对应像素点拟合，得到了该系统的相位和高度的映射关系。
另外，该实验中还对系统进行了精度测量。如图15所示，实验就一个3D打印的三分之一球进行三维重构，其中，该球半径为25 mm，截取该球上三分之一进行打印，打印精度为毫米量级，图中绿点为重构得到的三维点云数据，使用该点云数据进行球面拟合，拟合结果为渐变球面，拟合得到的球面半径为24.704，拟合均方差值为0.118。图中也显示了使用点云数据减去拟合球之后的误差值，可以看出，误差分布在1 mm量级之内。
图 14 单像素数字光栅三维成像结果图
Figure 14. Results of 3D single pixel imaging based on digital grating
需要提到的是，在物体进行重构过程中，由于条纹投影轮廓术要求探测物体，投影部分以及探测部分构成三角关系才能够将深度信息调制到二维光强信息中。而投影与探测部分之间夹角过大将会导致探测面积变形，从而影响到最终重构物体相对尺寸比例不统一。为了解决这个问题，该系统进行进一步的标定过程，将探测端的像素分布与投影端进行映射，从而实现了梯形校正，然后，实验系统还将投影坐标系映射到距离坐标中，从而可以直接得到物体的实际距离值，如图15所示。
图 15 球面的三维重建及相应的误差
Figure 15. 3D reconstruction of a spherical surface and corresponding error
-
正如前文所述，与经典的可见光成像系统相比，近红外成像系统因为红外波段具有较好的穿透能力，该系统在云雾环境和生物组织成像等情况下应用广泛，其肉眼不可观察的特点也在安全监控等领域得到了足够的关注。
但与传统的可见光阵列式探测器相比，红外波段探测器成本更高，工艺难度也更大，因此，单像素式的红外成像具有很大的应用前景。而逐点扫描技术具有较高信噪比，作为一种经典的单像素成像技术，在远距离成像，遗迹文物保护等领域有了很好的发展。
红外扫描式三维成像系统如图16所示，该系统可以分为扫描式照明部分和单像素探测系统两部分。照明部分采用波长为1064 nm，功率为9.5 mW的近红外激光器出射连续光到2D扫描振镜器件上，其最大扫描频率为1 kHz；单像素探测部分则包括焦距为35 mm的红外成像镜头，每毫米四线对的红外光栅，红外波段单像素探测器（InGaAs）以及其前方的收集透镜。
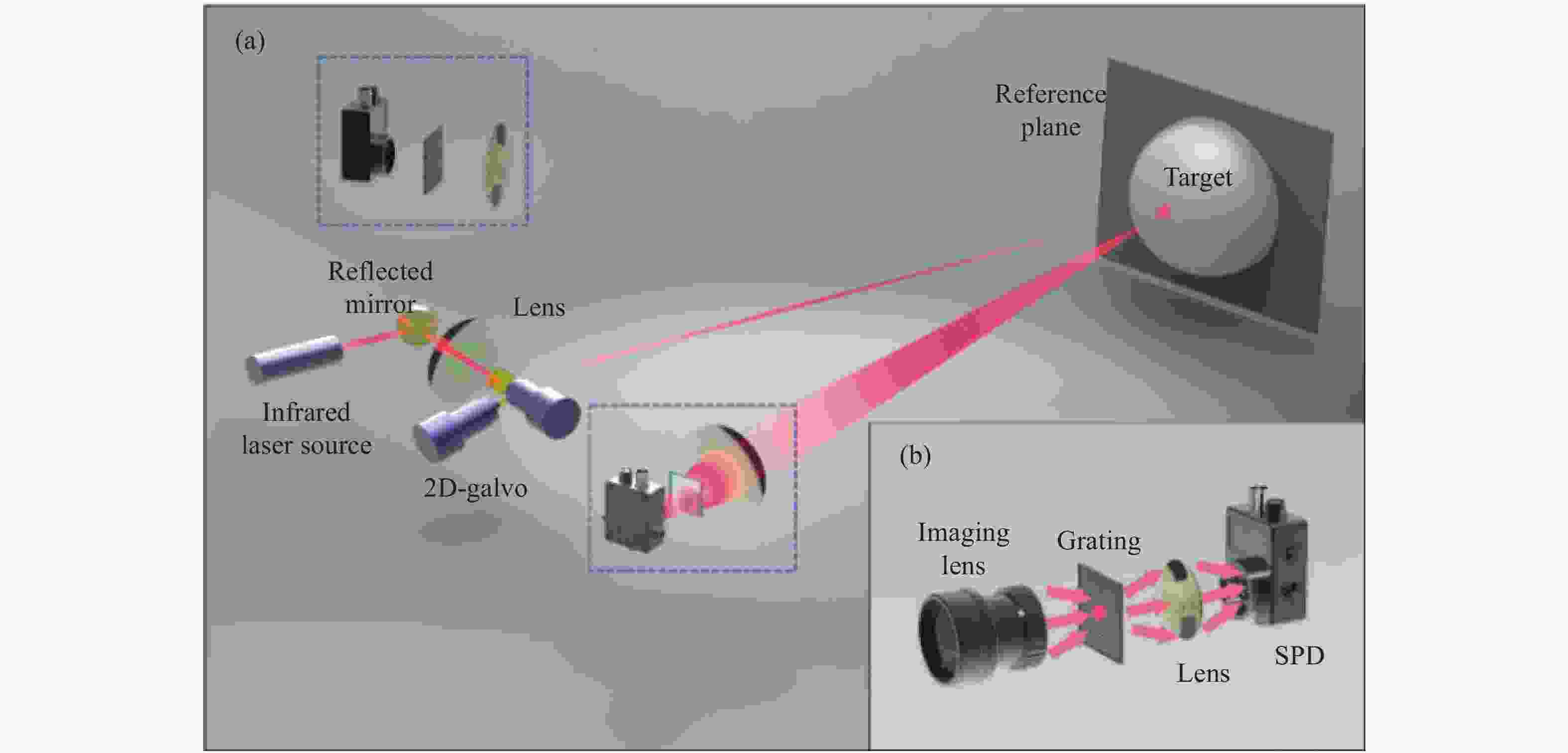
图 16 (a)基于扫描的红外三维单像素成像实验原理图；(b)单像素探测部分包括一个单像素探测器，一个成像镜头，一个光栅和一个汇聚透镜
Figure 16. (a) Schematic diagram of infrared 3D single-pixel imaging based on raster scanning; (b) Singe-pixel detection part includes a single-pixel detector, an imaging lens, a grating and a collecting lens
与前文提到的傅里叶单像素三维成像过程类似，该成像系统同样满足亥姆霍兹互易律。不具备空间分辨能力的单像素探测器将决定所得图像的光影分布，而以扫描方式具备空间分辨率的照明部分将决定获取图像的视场分布。
相比于经典的面阵探测器，在假设出射光源强度一致且不考虑噪声的前提下，扫描式单像素采样系统重构图像信噪比更高，因此扫描系统是在牺牲成像时间成本的前提下，提高了成像质量和精度。
三维物体的重构过程采用的是经典的条纹投影轮廓术方式，对二维亮度图进行快速傅里叶变换之后，使用滤波窗口提取傅里叶域一级频谱，得到的一级频率分量进行逆傅里叶变换得到相位图，最后通过相位展开算法和系统高度标定过程，得到物体的高度信息。
图17展示了笔者等使用上述红外成像系统对一个石膏人脸进行成像的结果。实验中采用了位于不同位置的两套相同的单像素探测器，在同一组条纹投影条件下同时对目标进行信号采集及三维重构。两个探测器分别放置在与物体处在同一水平面的左右两侧。根据前文提到的亥姆霍兹互易律，二位重构结果的光影分布将由不具备空间分辨能力的单像素探测器来决定，因此，不同方位放置的探测器将会得到完全不同的阴影分布情况。 这一特性可以从图中二维条纹图得到证实。同时，位于不同空间位置的探测器所得到的三维图像有差别，即三维重构存在误差。由于系统采用同一套照明设备，不同探测器得到的三维重构图在二维图像所在平面上是完全一一对应的。利用这一性质，可以将不同点探测器得到的三维重构结果进行叠加平均。在不增加测量时间的条件下，通过增加单像素探测器并行探测的方式，尽可能的提高三维重构质量。图17的结果证实了这个原理的可行性。
图 17 分别使用两个探测器得到的二维条纹重构图和相位重构图（三维重建结果是建立在对两个探测器数据叠加的基础上的）
Figure 17. Reconstructions of 2D fringe images and phase distribution using two detectors(The 3D reconstruction is obtained by overlaying data from both of the two detectors)
-
文中主要对单像素成像的技术原理进行了剖析，并介绍了单像素成像在三维成像中的应用。笔者首先从单像素成像的原理入手，从数学和物理两个角度对单像素成像进行了分析介绍，并结合单像素成像的优势，介绍了当前单像素成像在特殊波段成像中的应用发展，尤其是近红外波段以及太赫兹波段，基于关联算法的单像素成像都有着其特殊的优势。在三维成像方面，单像素成像也有着极高的应用实现。借由相移和傅立叶变换轮廓术，可以实现高精度的单像素三维图像重构。依靠傅立叶基进行采样，可以极大地减少重构所需的采样次数，通过追加额外的单像素探测器，可以通过光度立体法重构物体三维信息，也可以用于避免阴影带来的投影条纹淹没所导致的相位解包裹错误，从而提升三维重构的质量。尽管目前单像素成像技术还有待于进一步的研究和完善，随着结构光调制器件的迅速发展，在不久的将来，相信单像素成像技术会发展成为计算成像领域中的一颗耀眼的新星。
Application and development of single pixel imaging in the special wavebands and 3D imaging
-
摘要: 与传统的面阵成像技术不同，单像素成像技术作为一种新型的计算成像技术，使用不具备空间分辨能力的桶探测器，结合空间光场调制技术，通过关联算法重构待成像物体的空间强度信息，在研究界得到了广泛的关注。近年来，单像素成像技术被广泛应用于各种波段的成像领域，尤其是在某些面阵探测器价格昂贵甚至无法制备的特殊波段，单像素成像技术逐步发展为一项低成本高成像质量的替代技术。并且，在三维成像技术中，大量基于单像素成像的相关研究工作也被相继提出。文中主要介绍了单像素成像技术的基本原理及应用发展历程，并着重介绍了其在条纹结构投影三维成像技术中的应用工作。Abstract: Different from traditional array-detector imaging technology, single pixel imaging(SPI) technology, which is considered as a novel computational imaging technology, uses a bucket detector with no spatial resolution capability and combines with the spatial light field modulation technology to reconstruct the intensity of the object by correlation algorithm, which has received extensive attention. In recent years, SPI has been widely used with different light source, especially in some special wavebands, where the array-detectors are expensive or even impossible to be made. SPI has gradually developed into an alternative technology with low cost and high quality. In addition, a large number of works of SPI have been proposed in 3D imaging technology. The basic principle and application development of single pixel imaging was introduced. Its application in fringe projection 3D imaging was also introduced emphatically.
-
图 1 单像素成像原理图。(a)使用旋转毛玻璃的传统单像素成像；(b)计算单像素成像原理图
Figure 1. Diagram of single-pixel imaging. (a) Traditional single-pixel imaging using rotating ground glass; (b) Computational single-pixel imaging
图 2 调换探测器和光源位置后的光路原理图
Figure 2. Diagrams of optical path after exchanging position of detector and light source
图 3 单像素成像典型装置图及其成像结果。其中重构图片的分辨率均为128 pixel×128 pixel
Figure 3. Classical setup of single-pixel imaging and resulting images. All images are reconstructed with a resolution of 128 pixel×128 pixel
图 5 对甲烷气体的红外单像素成像原理图
Figure 5. Schematic diagram of infrared single-pixel imaging of methane gas
图 8 基于多个单像素探测器的三维成像原理图
Figure 8. Schematic diagram of 3D imaging based on multiple single-pixel detectors
图 9 不同视角下单像素探测器获得的重构图
Figure 9. Reconstructions of single-pixel detectors at differet points of view
图 10 整合面法线数据，叠加反射率数据后得到的重构面视图
Figure 10. Reconstructions after integrating the normal vectors and superimposing the reflectivity data
图 12 傅里叶单像素三维成像系统实验结果
Figure 12. Experimental results of Fourier 3D single-pixel imaging
图 13 单像素数字光栅三维成像系统图
Figure 13. 3D single-pixel imaging system based on digital grating
图 14 单像素数字光栅三维成像结果图
Figure 14. Results of 3D single pixel imaging based on digital grating
图 15 球面的三维重建及相应的误差
Figure 15. 3D reconstruction of a spherical surface and corresponding error
图 16 (a)基于扫描的红外三维单像素成像实验原理图；(b)单像素探测部分包括一个单像素探测器，一个成像镜头，一个光栅和一个汇聚透镜
Figure 16. (a) Schematic diagram of infrared 3D single-pixel imaging based on raster scanning; (b) Singe-pixel detection part includes a single-pixel detector, an imaging lens, a grating and a collecting lens
-
[1] Pelliccia D, Rack A, Scheel M, et al. Experimental x-ray ghost imaging [J]. Physical Review Letters, 2016, 117(11): 113902. doi: 10.1103/PhysRevLett.117.113902 [2] Yu H, Lu R, Han S, et al. Fourier-transform ghost imaging with hard X rays [J]. Physical Review Letters, 2016, 117(11): 113901. doi: 10.1103/PhysRevLett.117.113901 [3] Schori A, Shwartz S. X-ray ghost imaging with a laboratory source [J]. Optics Express, 2017, 25(13): 14822−14828. doi: 10.1364/OE.25.014822 [4] Tian N, Guo Q, Wang A, et al. Fluorescence ghost imaging with pseudothermal light [J]. Optics Letters, 2011, 36(16): 3302−3304. doi: 10.1364/OL.36.003302 [5] Tanha M, Ahmadi-Kandjani S, Kheradmand R, et al. Computational fluorescence ghost imaging [J]. The European Physical Journal D, 2013, 67(2): 44. doi: 10.1140/epjd/e2012-30341-8 [6] Radwell N, Mitchell K J, Gibson G M, et al. Single-pixel infrared and visible microscope [J]. Optica, 2014, 1(5): 285−289. doi: 10.1364/OPTICA.1.000285 [7] Edgar M P, Gibson G M, Bowman R W, et al. Simultaneous real-time visible and infrared video with single-pixel detectors [J]. Scientific Reports, 2015, 5: 10669. doi: 10.1038/srep10669 [8] Liu S, Yao X R, Liu X F, et al. Pile-up effect in an infrared single-pixel compressive LiDAR system [J]. Optics Express, 2019, 27(16): 22138−22146. doi: 10.1364/OE.27.022138 [9] Chan W L, Charan K, Takhar D, et al. A single-pixel terahertz imaging system based on compressed sensing [J]. Applied Physics Letters, 2008, 93(12): 121105. doi: 10.1063/1.2989126 [10] Ma Y, Grant J, Saha S, et al. Terahertz single pixel imaging based on a Nipkow disk [J]. Optics Letters, 2012, 37(9): 1484−1486. doi: 10.1364/OL.37.001484 [11] Ota S, Horisaki R, Kawamura Y, et al. Ghost cytometry [J]. Science, 2018, 360(6394): 1246−1251. doi: 10.1126/science.aan0096 [12] Xu Z H, Chen W, Penuelas J, et al. 1000 fps computational ghost imaging using LED-based structured illumination [J]. Optics Express, 2018, 26(3): 2427−2434. doi: 10.1364/OE.26.002427 [13] Zhao W, Chen H, Yuan Y, et al. Ultrahigh-speed color imaging with single-pixel detectors at low light level [J]. Physical Review Applied, 2019, 12(3): 034049. doi: 10.1103/PhysRevApplied.12.034049 [14] Studer V, Bobin J, Chahid M, et al. Compressive fluorescence microscopy for biological and hyperspectral imaging [J]. Proceedings of the National Academy of Sciences, 2012, 109(26): E1679−E1687. doi: 10.1073/pnas.1119511109 [15] Jin S, Hui W, Wang Y, et al. Hyperspectral imaging using the single-pixel Fourier transform technique [J]. Scientific Reports, 2017, 7: 45209. doi: 10.1038/srep45209 [16] Amiot C, Ryczkowski P, Friberg A T, et al. Supercontinuum spectral-domain ghost imaging [J]. Optics Letters, 2018, 43(20): 5025−5028. doi: 10.1364/OL.43.005025 [17] Rousset F, Ducros N, Peyrin F, et al. Time-resolved multispectral imaging based on an adaptive single-pixel camera [J]. Optics Express, 2018, 26(8): 10550−10558. doi: 10.1364/OE.26.010550 [18] Xiao F, Zhou L, Chen W. Direct Single-step measurement of Hadamard spectrum using single-pixel optical detection [J]. IEEE Photonics Technology Letters, 2019, 31(11): 845−848. doi: 10.1109/LPT.2019.2910172 [19] Zhao C, Gong W, Chen M, et al. Ghost imaging lidar via sparsity constraints [J]. Applied Physics Letters, 2012, 101(14): 141123. doi: 10.1063/1.4757874 [20] Ma S, Liu Z, Wang C, et al. Ghost imaging LiDAR via sparsity constraints using push-broom scanning [J]. Optics Express, 2019, 27(9): 13219−13228. doi: 10.1364/OE.27.013219 [21] Shi D, Yin K, Huang J, et al. Fast tracking of moving objects using single-pixel imaging [J]. Optics Communications, 2019, 440: 155−162. doi: 10.1016/j.optcom.2019.02.006 [22] Sun S, Lin H, Xu Y, et al. Tracking and imaging of moving objects with temporal intensity difference correlation [J]. Optics Express, 2019, 27(20): 27851−27861. doi: 10.1364/OE.27.027851 [23] Clemente P, Durán V, Tajahuerce E, et al. Optical encryption based on computational ghost imaging [J]. Optics Letters, 2010, 35(14): 2391−2393. doi: 10.1364/OL.35.002391 [24] Tanha M, Kheradmand R, Ahmadi-Kandjani S. Gray-scale and color optical encryption based on computational ghost imaging [J]. Applied Physics Letters, 2012, 101(10): 101108. doi: 10.1063/1.4748875 [25] Chen W, Chen X. Marked ghost imaging [J]. Applied Physics Letters, 2014, 104(25): 251109. doi: 10.1063/1.4879843 [26] Zafari M, Ahmadi-Kandjani S. Optical encryption with selective computational ghost imaging [J]. Journal of Optics, 2014, 16(10): 105405. doi: 10.1088/2040-8978/16/10/105405 [27] Zhu Y, Shi J, Li H, et al. Three-dimensional ghost imaging based on periodic diffraction correlation imaging [J]. Chinese Optics Letters, 2014, 12(7): 071101. doi: 10.3788/COL201412.071101 [28] Yu H, Li E, Gong W, et al. Structured image reconstruction for three-dimensional ghost imaging lidar [J]. Optics Express, 2015, 23(11): 14541−14551. doi: 10.1364/OE.23.014541 [29] Gong W, Zhao C, Yu H, et al. Three-dimensional ghost imaging lidar via sparsity constraint [J]. Scientific Reports, 2016, 6: 26133. doi: 10.1038/srep26133 [30] Zhang F, Zhang K, Cao J, et al. Study on the performance of three-dimensional ghost image affected by target [J]. Pattern Recognition Letters, 2019, 125: 508-513. [31] Sun M J, Zhang J M. Single-pixel imaging and its application in three-dimensional reconstruction: a brief review [J]. Sensors, 2019, 19(3): 732. doi: 10.3390/s19030732 [32] Mertz P, Gray F. Atheory of scanning and its relation to the characteristics of the transmitted signal in telephotography and television [J]. Bell System Technical Journal, 1934, 13(3): 464−515. doi: 10.1002/j.1538-7305.1934.tb00675.x [33] Chang P I, Huang P, Maeng J, et al. Local raster scanning for high-speed imaging of biopolymers in atomic force microscopy [J]. Review Of Scientific Instruments, 2011, 82(6): 063703. doi: 10.1063/1.3600558 [34] Stiff-Roberts A D, Chakrabarti S, Pradhan S, et al. Raster-scan imaging with normal-incidence, midinfrared InAs/GaAs quantum dot infrared photodetectors [J]. Applied Physics Letters, 2002, 80(18): 3265−3267. doi: 10.1063/1.1476387 [35] Pittman T B, Shih Y H, Strekalov D V, et al. Optical imaging by means of two-photon quantum entanglement [J]. Physical Review A, 1995, 52(5): R3429. doi: 10.1103/PhysRevA.52.R3429 [36] Gatti A, Brambilla E, Bache M, et al. Ghost imaging with thermal light: comparing entanglement and classical correlation [J]. Physical Review Letters, 2004, 93(9): 093602. doi: 10.1103/PhysRevLett.93.093602 [37] Shapiro J H. Computational ghost imaging [J]. Physical Review A, 2008, 78(6): 061802. doi: 10.1103/PhysRevA.78.061802 [38] Donoho D L. Compressed sensing [J]. IEEE Transactions On Information Theory, 2006, 52(4): 1289−1306. doi: 10.1109/TIT.2006.871582 [39] Emmanuel-J C, Wakin M B. An introduction to compressive sampling [J]. IEEE Signal Processing Magazine, 2008, 25(2): 21−30. doi: 10.1109/MSP.2007.914731 [40] Richard-G B. Compressive sensing [J]. IEEE Signal Processing Magazine, 2007, 24(4): 118. doi: 10.1109/MSP.2007.4286571 [41] Takhar D, Laska J N, Wakin M B, et al. A new compressive imaging camera architecture using optical-domain compression[C]//Computational Imaging IV. International Society for Optics and Photonics, 2006, 6065: 606509. [42] Duarte M F, Davenport M A, Takhar D, et al. Single-pixel imaging via compressive sampling [J]. IEEE Signal Processing Magazine, 2008, 25(2): 83−91. doi: 10.1109/MSP.2007.914730 [43] Magalhães F, Araújo F M, Correia M, et al. High-resolution hyperspectral single-pixel imaging system based on compressive sensing [J]. Optical Engineering, 2012, 51(7): 071406. doi: 10.1117/1.OE.51.7.071406 [44] Magalhães F, Araújo F M, Correia M V, et al. Active illumination single-pixel camera based on compressive sensing [J]. Applied Optics, 2011, 50(4): 405−414. doi: 10.1364/AO.50.000405 [45] Howland G A, Howell J C. Efficient high-dimensional entanglement imaging with a compressive-sensing double-pixel camera [J]. Physical Review X, 2013, 3(1): 011013. doi: 10.1103/PhysRevX.3.011013 [46] Noor I, Jacobs E L. Adaptive compressive sensing algorithm for video acquisition using a single-pixel camera [J]. Journal of Electronic Imaging, 2013, 22(2): 021013. doi: 10.1117/1.JEI.22.2.021013 [47] Chen H, Weng Z, Liang Y, et al. High speed single-pixel imaging via time domain compressive sampling[C]//CLEO: Applications and Technology. Optical Society of America, 2014: JTh2A. 132. [48] Torabzadeh M, Park I Y, Bartels R A, et al. Compressed single pixel imaging in the spatial frequency domain [J]. Journal of Biomedical Optics, 2017, 22(3): 030501. doi: 10.1117/1.JBO.22.3.030501 [49] Musarra G, Lyons A, Conca E, et al. Non-line-of-sight Three-dimensional imaging with a single-pixel camera [J]. Physical Review Applied, 2019, 12(1): 011002. doi: 10.1103/PhysRevApplied.12.011002 [50] Bacca J, Correa C V, Vargas E, et al. Compressive classification from single pixel measurements via deep learning[C]//2019 IEEE 29th International Workshop on Machine Learning for Signal Processing (MLSP). IEEE, 2019: 1-6. [51] Sun B, Edgar M P, Bowman R, et al. 3D computational imaging with single-pixel detectors [J]. Science, 2013, 340(6134): 844−847. doi: 10.1126/science.1234454 [52] Sun M J, Edgar M P, Gibson G M, et al. Single-pixel three-dimensional imaging with time-based depth resolution [J]. Nature Communications, 2016, 7: 12010. doi: 10.1038/ncomms12010 [53] Zhang Z, Liu S, Peng J, et al. Simultaneous spatial, spectral, and 3D compressive imaging via efficient Fourier single-pixel measurements [J]. Optica, 2018, 5(3): 315. doi: 10.1364/OPTICA.5.000315 [54] Jiang S, Li X, Zhang Z, et al. Scan efficiency of structured illumination in iterative single pixel imaging [J]. Optics Express, 2019, 27(16): 22499−22507. doi: 10.1364/OE.27.022499 [55] Sun B, Welsh S S, Edgar M P, et al. Normalized ghost imaging [J]. Optics Express, 2012, 20(15): 16892−16901. doi: 10.1364/OE.20.016892 [56] Sun B, Matt B, Richard V, et al. "Differential computational ghost imaging." Computational Optical Sensing and Imaging [J]. Optical Society of America, 2013: CTu1C.4. [57] Aβmann M, Bayer M. Compressive adaptive computational ghost imaging [J]. Scientific Reports, 2013, 3: 1545. doi: 10.1038/srep01545 [58] Shimobaba T, Endo Y, Nishitsuji T, et al. Computational ghost imaging using deep learning [J]. Optics Communications, 2018, 413: 147−151. doi: 10.1016/j.optcom.2017.12.041 [59] Wang Z, Zhu J. Single-pixel compressive imaging based on motion compensation [J]. IET Image Processing, 2018, 12(12): 2283−2291. doi: 10.1049/iet-ipr.2018.5741 [60] Satat G, Tancik M, Raskar R. Lensless imaging with compressive ultrafast sensing [J]. IEEE Transactions on Computational Imaging, 2017, 3(3): 398−407. doi: 10.1109/TCI.2017.2684624 [61] Ring E F J, Ammer K. Infrared thermal imaging in medicine [J]. Physiological Measurement, 2012, 33(3): R33. doi: 10.1088/0967-3334/33/3/R33 [62] Gregg V, Green R O, Chrien T G, et al. The airborne visible/infrared imaging spectrometer (AVIRIS) [J]. Remote Sensing of Environment, 1993, 44(2-3): 127−143. doi: 10.1016/0034-4257(93)90012-M [63] Gerald C H. Testing and Evaluation of Infrared Imaging Systems[M]. New York: JCD Pub., 1998. [64] E-Neil L, Treado P J, Reeder R C, et al. Fourier transform spectroscopic imaging using an infrared focal-plane array detector [J]. Analytical Chemistry, 1995, 67(19): 3377−3381. doi: 10.1021/ac00115a003 [65] Wood R A, Han C J, Kruse P W. Integrated uncooled infrared detector imaging arrays[C]//IEEE, 1992: 132-135. [66] Favro L D, Han X, Ouyang Z, et al. Infrared imaging of defects heated by a sonic pulse [J]. Review of Scientific Instruments, 2000, 71(6): 2418−2421. doi: 10.1063/1.1150630 [67] Bryan F J, Plassmann P. Digital infrared thermal imaging of human skin [J]. IEEE Engineering In Medicine and Biology Magazine, 2002, 21(6): 41−48. doi: 10.1109/MEMB.2002.1175137 [68] Nasse M J, Walsh M J, Mattson E C, et al. High-resolution Fourier-transform infrared chemical imaging with multiple synchrotron beams [J]. Nature Methods, 2011, 8(5): 413. doi: 10.1038/nmeth.1585 [69] Gibson G M, Sun B, Edgar M P, et al. Real-time imaging of methane gas leaks using a single-pixel camera [J]. Optics Express, 2017, 25(4): 2998−3005. doi: 10.1364/OE.25.002998 [70] Shrekenhamer D, Watts C M, Padilla W J. Terahertz single pixel imaging with an optically controlled dynamic spatial light modulator [J]. Optics Express, 2013, 21(10): 12507−12518. doi: 10.1364/OE.21.012507 [71] Watts C M, Shrekenhamer D, Montoya J, et al. Terahertz compressive imaging with metamaterial spatial light modulators [J]. Nature Photonics, 2014, 8(8): 605. doi: 10.1038/nphoton.2014.139 [72] She R, Liu W, Lu Y, et al. Fourier single-pixel imaging in the terahertz regime [J]. Applied Physics Letters, 2019, 115(2): 021101. [73] Takashi Y, Kawada Y, Toyoda H, et al. Terahertz movies of internal transmission images [J]. Optics Express, 2007, 15(23): 15583−15588. doi: 10.1364/OE.15.015583 [74] Zhang Y, Zhang J, Jiang C. Algorithm of scanning terahertz imaging on computer [J]. Computer Engineering and Applications, 2008, 44(11): 234−236. [75] Yi M, Kim H, Jin K H, et al. Terahertz substance imaging by waveform shaping [J]. Optics Express, 2012, 20(18): 20783−20789. doi: 10.1364/OE.20.020783 [76] Stantchev R I, Sun B, Hornett S M, et al. Noninvasive, near-field terahertz imaging of hidden objects using a single-pixel detector [J]. Science Advances, 2016, 2(6): e1600190. doi: 10.1126/sciadv.1600190 [77] Joel G, Krishnamurthy K, Brady D. Compressive single-pixel snapshot x-ray diffraction imaging [J]. Optics Letters, 2014, 39(1): 111−114. doi: 10.1364/OL.39.000111 [78] Chen S. X-ray 'ghost images' could cut radiation doses Technique points to safer medical imaging done with cheap, single-pixel cameras [J]. Science, 2018, 359(6383): 1452. doi: 10.1126/science.359.6383.1452 [79] Thomas A S, Shih Y, Wang Z, et al. From optical to X-ray ghost imaging [J]. Nuclear Instruments & Methods in Physics Research Section A-accelerators Spectrometers Detectors and Associated Equipment, 2019: 935173−177. [80] Margie P O, Paganin D M, Yin C, et al. Phase-sensitive x-ray ghost imaging [arXiv] [J]. arXiv, 2019: 6. [81] Alan B. Stereoscopic images in confocal (tandem scanning) microscopy [J]. Science, 1985, 230(4731): 1270−1272. doi: 10.1126/science.4071051 [82] Robert J W. Photometric method for determining surface orientation from multiple images [J]. Optical Engineering, 1980, 19(1): 191139. [83] Ronen B, Jacobs D, Kemelmacher I. Photometric stereo with general, unknown lighting [J]. International Journal of Computer Vision, 2007, 72(3): 239−257. doi: 10.1007/s11263-006-8815-7 [84] Kristin J D, Van G B, Nayar S K, et al. Reflectance and texture of real-world surfaces [J]. ACM Transactions on Graphics (TOG), 1999, 18(1): 1−34. doi: 10.1145/300776.300778 [85] Berthod K P H. Height and gradient from shading [J]. International Journal of Computer Vision, 1990, 5(1): 37−75. doi: 10.1007/BF00056771 [86] Zhang Y, Edgar M P, Sun B, et al. 3D single-pixel video [J]. Journal of Optics, 2016, 18(3): 35203. doi: 10.1088/2040-8978/18/3/035203 [87] Zhang Z, Ma X, Zhong J. Single-pixel imaging by means of Fourier spectrum acquisition [J]. Nature Communications, 2015, 6(1): 6225. [88] Mitsuo T, Mutoh K. Fourier transform profilometry for the automatic measurement of 3-D object shapes [J]. Applied Optics, 1983, 22(24): 3977. doi: 10.1364/AO.22.003977 [89] Max B, Wolf E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light[M]. New York: Elsevier, 2013. [90] Zhang Z, Zhong J. Three-dimensional single-pixel imaging with far fewer measurements than effective image pixels [J]. Optics Letters, 2016, 41(11): 2497−2500. doi: 10.1364/OL.41.002497 -
点击查看大图
计量
- 文章访问数: 2356
- HTML全文浏览量: 1087
- 被引次数: 0
