人类所处的物理世界空间是三维的，对三维信息的获取和处理技术体现了人类对客观世界的把握能力，因而从某种程度上来说它是体现人类智慧的一个重要标志。传统光探测器仅对被测场景的二维强度敏感而无法感知其三维形貌与深度信息。人类虽可通过自己的双眼来感知三维的世界，但无法对客观事物的三维形貌进行准确量化的描述。三维成像与传感技术作为感知真实三维世界的重要信息获取手段，为重构物体真实几何形貌及后续的三维建模、检测、识别等方面提供数据基础。近年来，随着计算机技术、光学和光电技术的发展，以光信号为载体的光学三维传感技术，融合光电子学、图像处理、计算机视觉与现代信号处理等多学科为一体，已发展成为光学计量和信息光学的最重要的研究领域和研究方向之一。

三维信息获取与处理技术以各种不同的风貌与特色渗透到我们身边的众多领域之中^[1–4]。在工业设计中，基于三维数字化模型的逆向设计方法可快速获得现有成熟产品的准确和完整的计算机模型，大大缩短产品或模具的研发周期。在虚拟现实领域，大量景物的三维彩色模型化数据已被以用于国防、模拟训练、科学试验、3D动画的建构。在医学整形领域，三维数字化技术已广泛用于面部软组织形态修复、外科检测、假牙假肢的量身定做。文物保护领域中，三维彩色数字化技术能以不损伤物体的手段，获得文物的三维信息和表面色彩、纹理，便于长期保存与再现。但在某些领域，如三维测量加工、机器人导航、快速逆向成型、自动化生产线控制、产品质量监控等，仅仅捕获待测物体的三维信息是不够的，三维数据获取的速度与效率直接关系到制造系统的响应能力、产品研制生产能力、以及产品质量保证能力。此外诸如在压模件尺寸监测、冲压板几何形状和形变检测、机车冲撞试验、压力波传播、不连续边界的应力集中、汽车制导中障碍检测、流体力学、流程可视化、运动力学、高速旋转等，这些高速瞬态过程的三维数据快速记录与准确定量再现将有助于描绘和分析动态过程中物体表面三维形态的变化，并为进一步提取与被测物体相关的结构、形变、应力等物理参量提供数据基础。

条纹投影三维成像因其非接触、高精度、全场测量、点云重建效率高等优点，已成为目前三维传感技术中的主流光学方法^[5–7]。然而现有研究工作大多集中在静态物体或缓变场景的形貌测量上，通过投影多组光栅条纹并结合格雷码/时间相位展开方法以获取绝对相位信息。这不可避免地延长了数据获取的时间，使其难以对动态物体或者变化场景达到快速响应。如何快速、准确、无歧义地获取目标，特别是运动目标的三维形貌信息是当前条纹投影轮廓术领域的一个亟待解决的问题。该问题直接制约着数字光栅投影技术的适用对象与应用范围，也逐渐成为该领域的研究热点之一^[8–11]。

2016年，以围棋界AlphaGo击败李世石开始^[12]，以深度学习为代表的人工智能（AI）技术全面进入了大众的视野，对于它的讨论变得更为火热起来；整个业界普遍认为，它很可能带来下一次科技革命，并且在未来可预见的10多年里，将深刻地改变人们的生活。正如当时的预测，目前人工智能已经在计算机视觉、图像语音处理等多个领域的技术上取得了全面的突破^[13–19]。与此同时，深度学习技术也在光学成像、计算成像、全息显微等领域逐步渗透^[20–27]，且展现出巨大的潜力。对基于条纹投影的三维成像而言，深度学习技术已成功应用于条纹图像的包裹相位求解、空域/时域包裹相位展开、条纹去噪、超快三维测量等方面。这些应用向大众展现了在人工智能的辅助下，条纹投影技术在效率、精度等方面取得的新突破。

文中首先将回顾条纹投影三维成像的基本原理。随后将列举深度学习技术在条纹投影三维成像中的典型应用。最后，从神经网络的可解释性、神经网络结构设计、神经网络训练数据获取等五个方面，分析与总结利用深度学习技术实现条纹投影成像面临的挑战和未来的走向。

条纹投影三维成像技术通过将立体视觉中一个摄像机替换成光源发生器（如投影仪）而实现，原理如图1所示。光源向被测物体投影按照一定规则和模式编码的图像，形成主动式三维形态测量。编码图案受到物体表面形状的调制而产生形变，而带有形变的结构光被另外位置的相机拍摄到，通过相机投影光源之间的位置关系和结构光形变的程度可以确定出物体的三维形貌。条纹投影技术本质上区别于干涉测量技术，但它采用的条纹形式和干涉测量中两束相干光干涉产生的原理相类似。相比于立体视觉法，其最大优点在于求解物体初相位时是点对点的运算，即在原理上中心点的相位值不受相邻点光强值的影响，从而避免了物面反光率不均匀或观察视角的偏差引起的误差，测量精度可以达到几十或几个微米。

图  1  条纹投影三维成像原理图

Figure 1.  Diagram of fringe projection 3D imaging

条纹投影技术大体上包含系统标定与三维成像两个方面。系统标定的目的在于获取相机与投影仪的内外参数，为相位与三维坐标转换提供参考系^[28-29]。而另一部分三维成像的目的在于通过分析采集的光栅图像，求解相位信息，结合系统标定部分获得的参数进行相位深度之间的转换，完成三维模型重建。文中将简要回顾三维成像部分的基本原理。该部分可细分为三个步骤：条纹分析、相位展开、相位与三维坐标转换。

条纹投影技术通常采用正弦条纹图像作为照明图案对被测表面进行编码，采集的条纹图案一般可表示为：

式中：$ (x,y)$为像素坐标；$ A$为背景光强；$ B$为调制度；$ \phi$为相位。傅立叶轮廓术^{[30, 8]}是一种常用的条纹分析方法，通过利用带通滤波器提取光栅频谱的正负一级谱，可获得：

随后，利用反正切函数计算相位$ \phi$

需要注意的是傅立叶轮廓术是一种基于空间滤波的相位计算方法。尽管效率高，但通常假设被测表面为平滑表面，并且需要投影光栅的空间频率足够高^[30]。

相移轮廓术^[31]是另一种经常使用的光栅条纹分析法，以使用最为广泛的N步相移法为例，相机拍摄一系列具有$ 2{\text{π}} /N$相对相移的光栅图像

式中：$ n$为相移指数（$ n = 1,2, \ldots ,N$）。当拍摄的图像大于三幅时（即$ N \geqslant 3$），利用最小二乘法^[32]，可计算物体相位$ \phi $：

与傅立叶轮廓术相比，相移法的优势在于相位解算精度高。更进一步，随着相移步数的增加，光栅图像的噪声^[31]、系统的非线性（如投影仪的Gamma）^[33]以及光栅图像的饱和问题^[34]对相位计算造成的影响都将减小。

无论是傅立叶轮廓术（公式(3)），还是相移轮廓术（公式(5)），解调得到的相位均是包裹相位。它的空间分布是截断的，存在$ {2{\text{π}}}$相位跳变。为了获得连续的真实空间相位分布，需要对其进行相位展开

式中：$ \varPhi (x,y)$为去包裹相位或展开相位；$ k(x,y)$为光栅条纹的级次。

相位展开算法目的在于确定光栅条纹的级次$ k(x,y)$。根据求取条纹级次的原理不同，常见的相位展开方法可以被分为空域展开法^[35]与时域展开法两类^[36]。空域相位展开是指利用相邻像素的相位值所提供的约束来计算绝对相位值，但该方法依赖于被测物体表面连续的假设。如果被测场景中包含多个孤立物体，或者被测物存在处于不连续表面边界的相邻像素的绝对相位值相差超过$ {2{\text{π}}}$，则存在条纹级次歧义，从而无法正确展开。与空间相位展开相比，时间相位展开中每个像素的条纹级次都在时间轴上独立计算，无需参考邻近像素，因此可以展开任意复杂形状表面的包裹相位值。但就相位展开的效率而言，时间相位展开通常还需要至少一幅额外的参考相位图。

若将投影仪看做“反相机”来处理，根据双目视觉原理^[37]，对于相机存在如下投影关系：

对于投影仪存在如下投影关系

将展开后的相位$ \varPhi (x,y)$作为线索，可构建相机坐标与投影仪坐标之间的关系：

式中：$ \alpha $为缩放因子；$ K$为内参；$ R$为旋转矩阵；$ t$为平移向量；$ f_0$为光栅频率；$ w^p$为投影仪分辨率。在预先矫正系统的畸变后，通过联立公式(7)~(9)，可获得的相机像素$ {(x,y)}$对应的三维坐标$ (X,Y,Z)^T$。

至此，笔者简要回顾了条纹投影的基本原理。这些基本原理构成了条纹投影技术的物理模型。传统的条纹投影技术是在“物理（模型）”驱动下的技术。下面将介绍通过运用深度学习技术，条纹投影技术也可成为一种在“数据”驱动下的技术，并且在这种情况下，它展现出了超越传统算法的能力。

光栅条纹分析的目的在于解调光栅中蕴含的与深度信息相关的相位信息。单幅光栅条纹分析，也就是空域相位解调法，具有天然的高时域分辨率优势。传统的单帧条纹分析法包括：傅立叶分析法^[30]、加窗傅立叶法^[38]、小波分析法^[39]等。由于所有能运用的解调手段只能局限于一张信息量有限的光栅图像之中，传统的单帧条纹分析方法一般只适合处理表面高度变化平缓的物体，对轮廓陡变、不连续以及物体细节丰富的区域较为敏感。针对轮廓复杂的物体，难以实现高精度、高分辨率的相位测量。此外这类算法在实施过程中通常需要操作者手动地设定与调节算法参数，因此它们难以完全实现全自动化操作。由于相位解调的结果与算法参数设定有较大关系，对于初学者而言，他们往往难以迅速获得理想的相位解调结果。

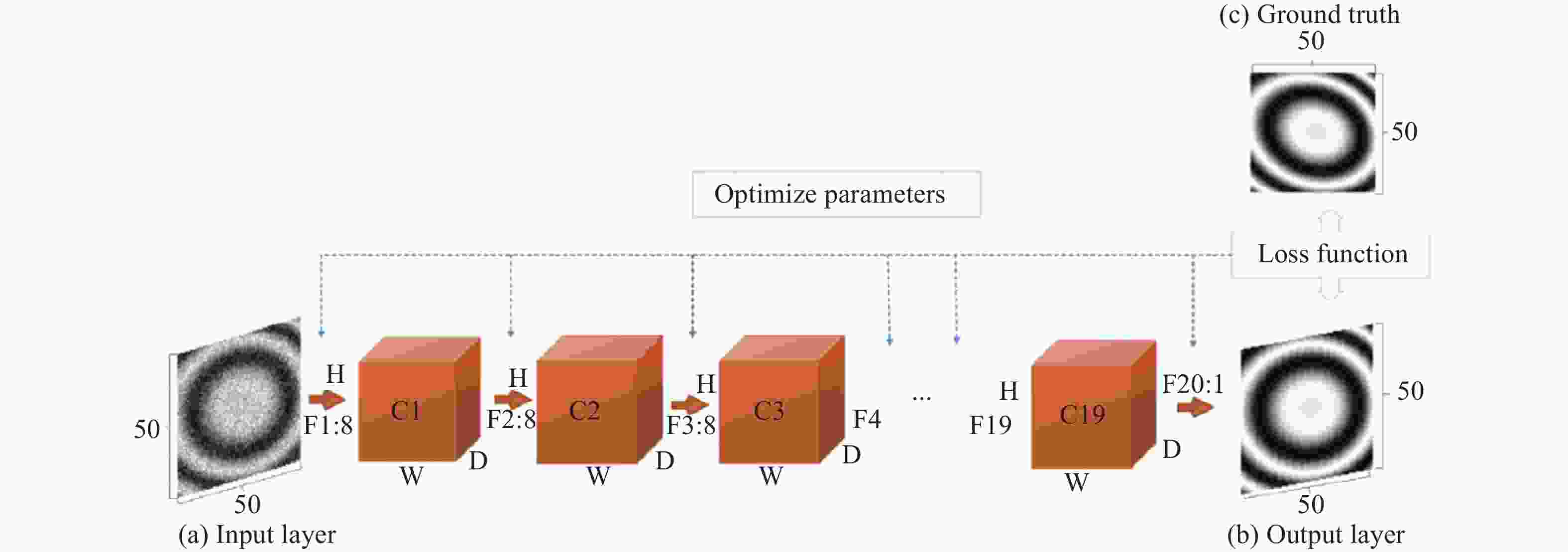
为了克服这些问题，Feng等人^[40]提出了一个基于深度学习框架的单帧光栅条纹分析法。该方法的思想在于仅采用一张条纹图像作为输入，利用深度神经网络来模拟时域相移法的相位解调过程。如图2所示，结合光栅图像的公式(1)，通过构建两个卷积神经网络（CNN1和CNN2），CNN1负责从输入条纹图像（I）中提取背景信息（A）。随后CNN2利用提取的背景图像（A）和原始输入图像（I）生成所需相位的正弦部分（M）与余弦部分（D）。最后，将该输出的正余弦结果带入反正切函数计算得到最终的相位分布。为了给深度神经网络树立一个“优秀”的学习对象，该文作者以标准12步相移算法作为学习目标，通过对各类不同的大量样本进行训练，两个卷积神经网络学习各类型条纹图像中相位相关特征的提取。经过适当的训练之后，它们就可以被用于对单幅条纹图像进行全自动分析并且输出对应的高精度相位分布。

图  2  利用深度神经网络解调单幅条纹图像中的相位信息流程图^[40]

Figure 2.  Flowchart of phase calculation from a single fringe image using deep neural network^[40]

实验结果表明，对于复杂表面，基于深度学习的条纹分析技术能够达到传统傅立叶变换法和加窗傅立叶变换法难以实现的相位解调精度（相位误差降低50%以上），且能够有效保持物体边界与轮廓的细节，总体测量效果接近于12步相移法（如图3所示）。由此可见，该方法为实现“高精度、高效率、全自动”的条纹投影或相位恢复提供了一条切实可行的方案。仅采用单一条纹图像作为输入，深度神经网络即可快速生成对应的高精度相位分布。整个过程全自动、无需人工干预。

图  3  三维重建结果对比^[40]。（a）傅立叶变换法^[30]，（b）加窗傅立叶变换法^[38]，（c）基于深度学习的条纹分析法，（d）12步相移法

Figure 3.  Comparison of 3D reconstruction results^[40]. (a) Fourier transform profilometry, (b) windowed Fourier transform profilometry, (c) fringe analysis based on deep learning, and (d) 12-step phase-shifting profilometry

同样为了实现针对单幅光栅图像的包裹相位恢复，Shi等人^[41]提出了一种基于标签增强与区域分块的深度学习条纹分析技术。Shi等人建议将原始大小（如512×512分辨率）的图片，划分成更小且具有邻域交叠（如40×40分辨率）的小图片作为神经网络的输入数据进行相位恢复的训练。由于图片更小，神经网络的训练对于设备的硬件要求可有所降低。相位恢复方面，该方法同样利用深度学习模型进行相位计算的中间变量（光栅条纹的余弦信息）提取。随后，该方法对得到的中间变量进行Hilbert变换与反正切函数计算，获取最终的包裹相位信息。作为一种监督式的神经网络学习，为了使神经网络能更好地学习与模仿正确的包裹相位解调，研究人员需要尽可能地制作高精度的标签数据。为达到这一目的，Shi等人提出首先通过四步相移法得到所需的标签数据，然后采用Shearlet变换法对得到标签数据进行滤波，实现光栅中噪声信号的抑制。图4展示了该方法的流程图。

为了证明该方法的有效性，Shi等人对运动的手掌进行了三维测量。他们选取了运动过程中的六个不同时刻，然后利用神经网络重建相位信息。作为对照，还采用了传统的傅立叶轮廓术（FT）进行相位提取。相位重建结果如图5所示。实验表明相比于传统的傅立叶变换轮廓术，该方法（DNN）可更为准确的提取运动手掌的相位信息。

图  4  基于标签增强与区域分块的深度学习条纹分析的相位反演流程图^[41]

Figure 4.  Flowchart of label enhanced and patch based deep learning fringe analysis for phase retrieval^[41]

图  5  用FT法和DNN法对六个不同时刻的运动手掌进行了相位测量^[41]

Figure 5.  Phase measurement of hand movement at six different moments by FT and DNN methods^[41]

对于基于条纹图像分析的相位恢复方法，如条纹投影、干涉测量、全息术等，噪声的存在会降低图像的条纹信号信噪比，进而影响相位恢复的准确性。Yan等人^[42]提出了利用深度学习算法来降低条纹图的噪声。图6显示了该方法的流程图。该方法的核心在于构建一个层数为20的深度卷积神经网络。图6（a）为具有噪声的光栅图，它是整个神经网络的输入数据。该输入随后经过一系列的串联卷积神经网络，最后输出噪声得到抑制的光栅图（图6（b）所示）。该网络的训练方式为监督式训练，使用的训练标签为不含任何噪声的仿真光栅图（图6（c）所示）。

为验证该方法的有效性，Yan等人利用训练好的神经网络预测了六组不同的含噪声条纹图。结果如图7所示。图7（a）显示了含有噪声的原始条纹图，图7（b）显示了不含噪声的标准条纹图，图7（c）为利用深度学习法计算得到的去噪后条纹图。与标准结果相比，不难发现深度学习算法成功地学习了如何去除噪声。此外，基于深度学习向前计算的优势，整个去噪算法的执行速度相比传统方法更快。作为训练数据的生成，该方法采用了计算机仿真的方式进行生成。尽管效率高，但是可节省操作人员的大量时间。但是实际的光栅图与仿真的光栅图存在差异，此差异将对算法的性能提出更高的要求。

图  6  基于深度学习的条纹图像去噪方法原理图^[42]

Figure 6.  Diagram of fringe image denoising using deep learning^[42]

图  7  神经网络的测试结果^[42]。（a1）、（a2）带有噪声的仿真条纹图；（b1）、（b2）不含噪声的条纹图；（c1）、（c2）用深度学习去噪后的结果

Figure 7.  Test results^[42]. (a1), (a2) Simulation fringe pattern with noise; (b1), (b2) fringe pattern without noise; (c1), (c2) denoised results with deep learning

如1.2节所述的基本原理，相位展开法大体上分为空域相位展开和时域相位展开两类。按照这一方法分类，基于深度学习的相位展开方法也可同样划分为空域法和时域法。

Spoorthi G.E.等人^[43]提出了一个基于相位神经网络（PhaseNet）用于实现二维的空域相位展开。该方法的原理如图8所示。该网络的输入为包裹相位，通过构建的神经网络DCNN，使其输出条纹级次（即包裹计数）。该网络由一个编码器、一个对应的解码器和一个像素级分类层组成。研究人员发现由于深度神经网络预测的条纹级次在包裹相位跳变周围区域和存在相位陡变的区域容易发生错误，他们继续提出了一个基于聚类的条纹级次后处理方法。该方法通过合并互补的方式来增强相位空间分布的平滑度。最后，原始的包裹相位结合优化后的条纹级次，可计算最终的展开相位。

图  8  基于PhaseNet的相位展开原理图^[43]

Figure 8.  Schematic of phase unwrapping using PhaseNet^[43]

为了验证该方法，研究人员首先利用展开后相位与条纹级次之间的关系，仿真生成了大量的训练数据。然后利用这些数据训练构建神经网络。神经网络训练结束后，研究人员又采用一组额外的仿真数据来测试该网络的表现。图9（a）显示了神经网络输入的包裹相位，图9（b）和图9（c）分别为利用神经网络计算和条纹级次优化后得到展开相位和条纹级次。此外，Spoorthi G.E.等人还发现该方法对于包裹相位中的噪声具有很好地抑制作用。相比于MATLAB自带的相位展开函数以及基于质量导向的相位展开法，该方法的展开相位误差更小。最后，得益于深度学习方法的一个先天优势，即训练结束后，神经网络的执行是无迭代、无搜索的向前传播计算，该方法的计算速度也比传统的基于质量导向方法更快。但是值得注意的是，在训练和测试过程中，该方法使用的数据同样来自仿真。由于实际的包裹相位情况通常比仿真的相位更加复杂，采用该方法在处理实际的或者更为复杂的包裹相位时还需要更为深入地调试与优化。

图  9  利用PhaseNet展开不同形状包裹相位得到的结果^[43]。（a）包裹相位；（b）展开相位；（c）PhaseNet输出的条纹级次

Figure 9.  Results of different wrapped shapes using PhaseNet^[43]. (a) Wrapped phase; (b) unwrapped phase; (c) fringe order with PhaseNet

为了解决相位展开过程中的噪声问题与采样不足引起的混叠问题，Wang等人^[44]也利用深度学习技术构建了相位展开神经网络。与PhaseNet不同，该方法采用的是具有U-Net结构的神经网络，该结构适用于训练数据样本较小的神经网络。图10展示了该方法的训练和测试过程。与PhaseNet相比，PhaseNet是利用神经网络预测条纹级次，再结合包裹相位计算展开后的相位。而该方法省去了计算条纹级次的这个中间步骤，直接预测包裹相位对应的去包裹相位。

图  10  神经网络的训练与测试^[44]。（a）训练；（b）测试

Figure 10.  Schematics of the training and testing of the neural network^[44]. (a) training; (b) testing

实验中研究人员对动态的蜡烛火焰进行了相位恢复，结果如图11所示。在实验过程中，火焰受到风扇的干扰，产生不同的相位分布。该图显示了动态蜡烛火焰的包裹相位、该方法（CNN）和LS方法在不同帧中重建的展开相位以及它们在20 s内在不同帧中的相位展开差异。实验表明该方法可成功地重建神经网络在训练阶段中未见过对象的包裹相位。

图  11  动态蜡烛火焰的包裹相位展开结果对比^[44]。Wrap表示包裹相位；CNN表示该方法获得的展开相位；LS表示最小二乘法获得的展开相位；Diff为CNN法与LS法计算结果之间的差异

Figure 11.  Comparison of results of phase unwrapping of dynamic candle flame^[44]. Wrap represents the wrapped phase; CNN represents the phase unwrapped by this method; LS represents the phase unwrapped by the least square method; Diff represents the difference between the results of CNN and LS methods

时域相位展开较空域相位展开相比具有恢复不连续或孤立物体表面包裹相位的优势。为了实现这一优势，通常需要采集不同频率光栅对应的多幅包裹相位。时域相位展开有三种代表性的方法^[36]：多频相位展开方法、多波长（外差）相位展开方法和数论相位展开方法。研究人员发现多频相位展开方法具有最高的展开可靠性和最佳的鲁棒性^[36]。

通常为了提高测量的效率，笔者需要使用尽量少的光栅图案。所以一种常见的做法是获取具有两个不同频率光栅的包裹相位。将它们简单地称为低频相位和高频相位。对于多频相位展开方法，通常低频光栅的频率为1，即投影光栅只包含一个正弦分布。由于三维重建模型最终来自于高频光栅，为了获得高精度的三维数据，需要尽可能地提升高频光栅的空间频率。但由于噪声等因素的影响，低频光栅相位的展开（辅助）能力有限，它难以正确展开频率大幅提升后的高频光栅包裹相位。

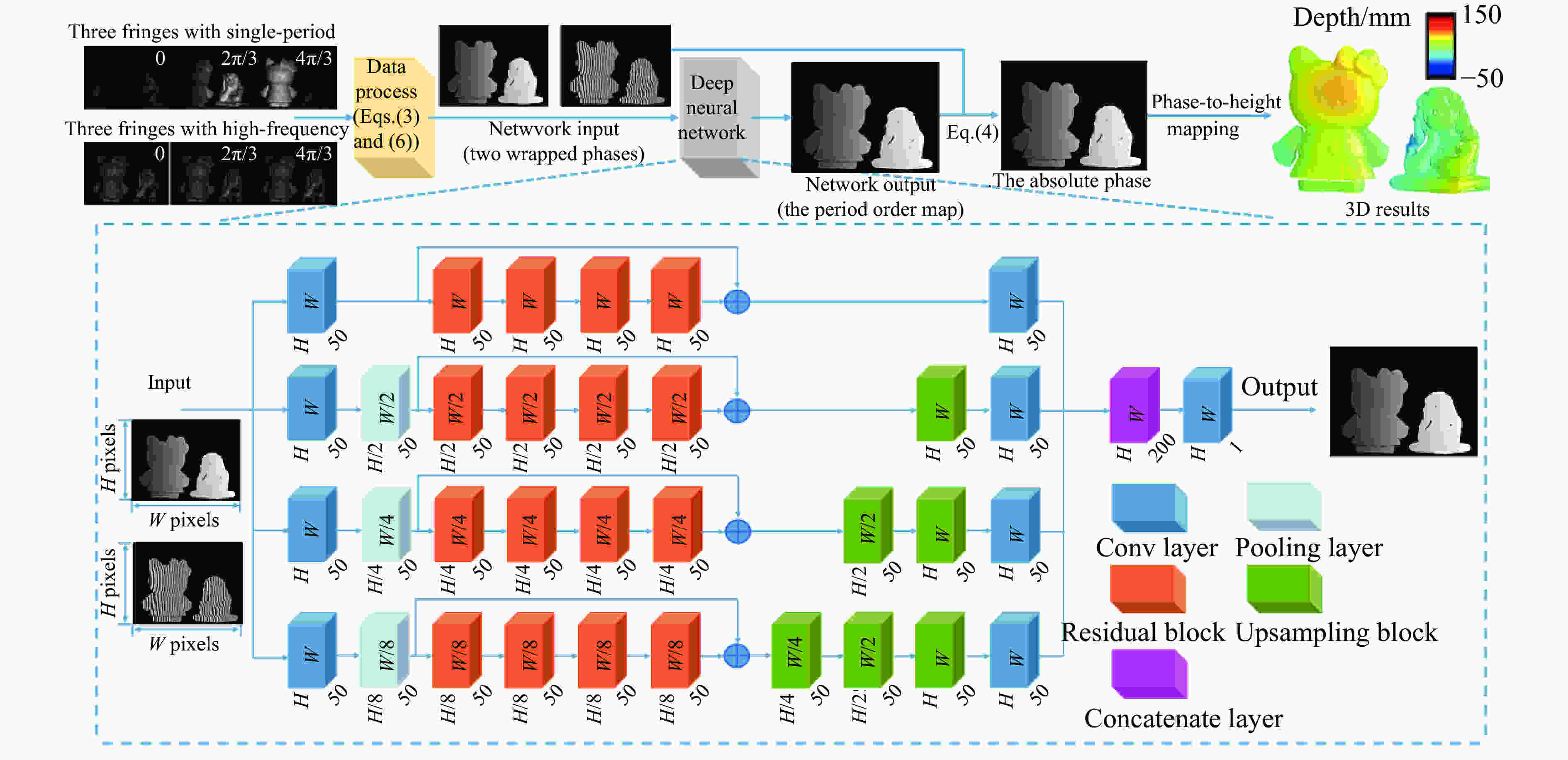
在不改变低频光栅的前提下，为了尽可能地提高可展开的高频光栅空间频率，Yin等人^[45]提出了基于深度学习的时域相位展开方法。如图12所示，首先利用三步相移法得到两个不同频率光栅对应的包裹相位。然后，将它们作为输入，送入构建的一个四路径的卷积神经网络。该网络经过训练后，可输出高频光栅包裹相位对应的条纹级次。最后结合高频包裹相位，进行相位展开，进而获得被测物体的三维数据。

图  12  基于深度学习的时域相位展开方法的示意图^[45]

Figure 12.  Schematic of temporal phase unwrapping using deep learning^[45]

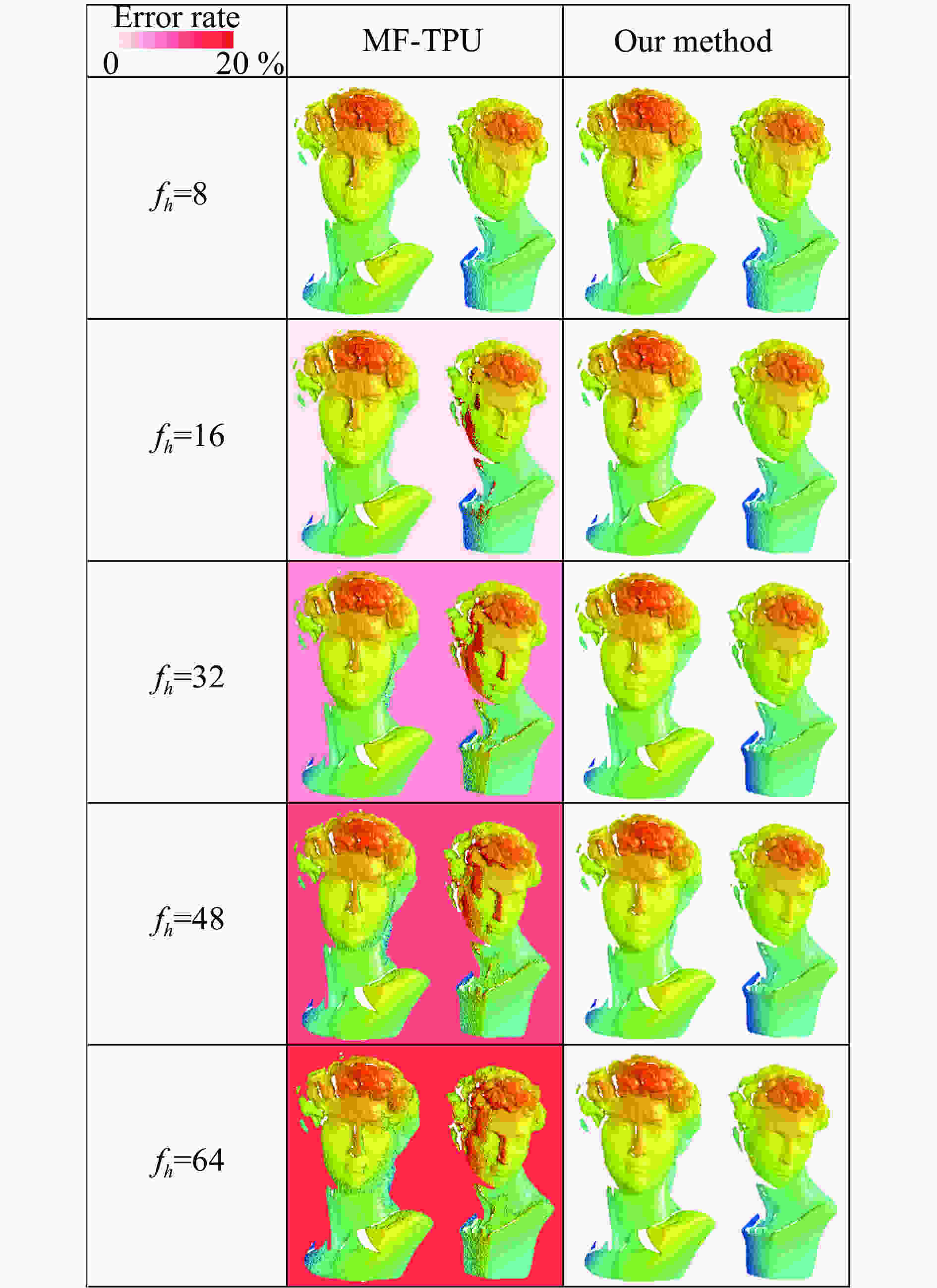
Yin等人比较了传统多频相位展开法（MF-TPU）与基于深度学习的时域相位展开法。图13显示了一组被测物体的相位展开后的3D重建结果，背景颜色的深浅显示了相位展开误差率的大小。当投影的高频光栅频率为16时，传统多频相位展开法开始表现出较为明显的去包裹错误。当频率持续增加时，相位展开错误率也随之明显增加。但对于基于深度学习的时域相位展开法，相位展开的错误率并未随光栅频率增加而显著增加。根据该实验结果，即使当高频光栅频率达到64，该方法的相位展开的正确率仍高于传统方法在频率为16时的正确率。由此可见，采用深度学习技术辅助后，时域多频相位展开的正确率可得到大幅提升。

图  13  针对不同的高频光栅包裹相位（例如频率分别为8、16、32、48和64），比较多频相位展开方法（图中MF-TPU）和基于深度学习的时域相位展开方法（图中Our method）的相位展开结果^[45]

Figure 13.  Comparison between traditional MF-TPU and the deep learning based method for high-frequency phase unwrapping (for example, the frequencies are 8, 16, 32, 48 and 64 respectively) ^[45]

在光学三维成像中，基于单幅图像的测量方法在测量速度和对运动伪影的鲁棒性等方面均优于基于多幅图像的结构光测量技术。Sam Vam Der Jeught等人^[46]提出了一种完全基于深度学习的单帧光栅解调方法，该方法可直接从一幅变形的光栅中解调处被测表面的高度（或深度）信息。该方法首先通过计算机仿真的方式，随机生成对应不同高度分布的扭曲光栅条纹。然后将这些的仿真数据输入构建的卷积神经网络，其结构如图14所示。输入的光栅图顺次经过10个卷积神经网络，最后输出对应的高度分布图。

为了训练该神经网络，Sam Vam Der Jeught等人随机生成了12 500幅高度分布图和与它们对应的扭曲光栅图。其中的10 000组数据用来训练网络，剩余的2 500组数据用来验证。在Titan X的GPU平台上，整个训练耗时接近12 h。图15给出了一组实验结果。该实验一共测试了三个对象：球面、三角斜面和人脸头像。从第四列的误差分析来看，对于球面和三角斜面这类变化较为简单的对象，均方根误差（RMSE）误差较小，而对于轮廓较为复杂的人脸模型，RMSE误差较大且超过了1%。

对于基于条纹投影的三维成像而言，该方法提出的是一个端对端的深度学习训练模型。对于“端对端”的训练策略，其优势在于将中间结果的计算过程（如包裹相位计算和相位展开）与最后的深度计算融合在了一起，使得轮廓计算一步到位。尽管高效，但由于部分中间结果，比如包裹相位，其存在固有的空间不连续性，使得神经网络往往难以直接对齐进行准确的拟合。尽管这一过程隐藏在了这个“端对端”的大框架下，但是从最后恢复的高度图来看，该方法的测量精度仍有很大的提升空间。此外，由于该方法同样是基于仿真数据进行的神经网络训练和验证，当其处理真实拍摄的光栅图像时，处理过程也许需要更为深入的优化。

图  14  从单幅条纹图解调高度信息的神经网络结构图^[46]

Figure 14.  Neural network structure diagram of height estimation from a single fringe image^[46]

图  15  针对球面、三角斜面和人脸头像光栅图的实验结果图^[46]。第一列为输入神经网络的条纹图；第二列为真实的高度分布；第三列为神经网络输出的高度分布；最后一列为根据第二列与第三列得出的误差分布图

Figure 15.  Experimental results of spherical, triangular bevel and face image grating^[46]. The first column is the fringe image of the input neural network; the second column is the true simulated height distribution; the third column is the height distribution of the output of the neural network; the last column is the error distribution map based on the second column and the third column

系统标定作为条纹投影中重要的一环一直都是本领域的研究重点。条纹投影系统将双目视觉系统的一个相机替换成投影仪，构建了一种主动式的“双目”视觉三维成像系统。为了重构三维坐标，将投影仪当做“反相机”来处理，然后运用现有双目成像的原理。然而，投影仪的镜头与相机的镜头在设计与功能上存在一定差异。因此严格地说起来，有时投影仪的标定并非能够简单地套用相机标定的模型。这种套用带来的其中一个问题是投影仪镜头畸变矫正问题，即相机的畸变模型难以准确标定投影仪的畸变，致使重建的三维轮廓出现失真。

为了解决这一问题，LV等人^[47]提出了一种基于深度学习的投影仪镜头畸变影响矫正方法。如图16所示，该方法首先采用传统标定方法，对投影仪和相机的畸变进行矫正，随后利用深度学习矫正剩余的投影仪畸变对三维轮廓造成的影响。

图  16  基于深度学习的投影仪畸变矫正流程图^[47]

Figure 16.  Flowchart for projector distortion correction with deep learning^[47]

LV等人提出了一个全连接神经网络，其输入为存在畸变残差的三维空间坐标$ {\left[ {x,y,z} \right]^{\rm{T}}}$，输出为该空间位置处的深度方向误差$ \Delta z$。通过该方法来补偿剩余畸变对三维重构造成的影响。研究人员利用训练好的模型对平板测量进行的验证，结果如图17所示。可以看出，经过矫正后，峰谷误差（PV）得到了较大幅度的下降。但是需要指出的是，该方法获取训练的标签数据依赖于对存在残余误差的平面三维数据进行平面拟合，来获得理想的平面三维数据。如果需要更加准确地确定畸变造成的深度误差，也许需要一种精度更高的方式来确定不同姿态下平板表面的真实三维数据。

图  17  测试数据结果^[47]。（a）原始数据的三维形状；（b）原始数据的误差分布；（c）校正后的数据三维形状；（d）校正后数据的误差分布

Figure 17.  Test results^[47]. (a) 3D shape of the original data; (b) error distribution of the original data; (c) 3D shape of the corrected data; (d) error distribution of the corrected data

高速摄影技术作为图像获取技术的一个重要分支，能够对各种瞬态过程进行记录，广泛应用于军工、航空航天等领域^[48]。尽管高速CMOS器件目前已能实现每秒万帧，甚至百万帧的拍摄，但仅能够获取二维平面图像数据。针对瞬态场景，如何从二维平面图像中获取三维深度图像，依旧是一个极具挑战性的世界性难题。为此Feng等人^[49]提出了微频移深度学习轮廓术，研制了基于数字光栅投影的瞬态三维轮廓测量系统，测量速度可达每秒20,000帧三维数据。

为了满足超快测量中相位信息的高效提取，高速三维成像中使用数量更少的光栅条纹对运动物体进行编码，可以减小物体运动对三维重建造成的干扰。同时为了确保三维重建的精度，该方法最终使用了三种不同的高频率光栅。该方法的原理如图18所示，首先利用深度学习算法计算这三幅光栅图中的相位信息，其中一幅用于重构三维轮廓，另外两幅用来辅助相位的绝对展开。最后根据标定的系统参数，重构光栅图像中蕴含的三维轮廓数据。

图  18  微频移深度学习轮廓术原理图^[49]

Figure 18.  Diagram of micro deep learning profilometry^[49]

为了测试该方法的有效性，Feng等人设置了一个瞬态场景。该场景由一个静态的石膏像和一个下落的乒乓球组成。相机拍摄速度为20 000 帧/s，记录了乒乓球落地与反弹的全过程。这两个物体均未在神经网络的训练过程中出现。图19的第一行显示了在不同时刻下拍摄的光栅图像。图19的第二行显示了该时刻对应的重构三维模型。可以看出整个乒乓球的下落过程不到0.1 s，根据三维重建的结果可知，针对不同的时刻，该方法成功地恢复了具有不同运动状态的物体轮廓。相比于传统超快三维成像方法，该方法表明得益于深度学习算法的强大运算能力，可在光栅图像数量减少的前提下，依然精确恢复物体的轮廓信息。因此基于人工智能的辅助，基于条纹投影的超快三维成像可朝着更高的时间与空间分辨率方向发展。

图  19  针对下落的乒乓球和静态石膏像进行的高速三维成像，速度为20 000 帧/s^[49]

Figure 19.  High speed 3D imaging of a falling table tennis and static plaster at speed of 20 000 frame/s^[49]

如第一章基本原理所介绍，条纹投影技术的三维成像部分主要包括条纹分析、相位展开、相位深度映射这几个方面。通过第二章至第五章的介绍，笔者发现当前研究人员正尝试着用深度学习技术替代传统方法以实现上述几个方面中的某一项内容，或者全部内容（端对端的策略）。然而对于大多数研究人员而言，深度学习方法预测最终结果的过程仍是一个“黑箱子”——只能通过最终的测试结果来判断神经网络的优劣。由于难以把握神经网络的推演机理，使得优化和提升神经网络性能的目标沦为了大量的试错。尤其是对于大规模的神经网络，巨量的参数使得完成一次训练通常需要数个昼夜甚至更久。多次且无明确方向的试错易造成时间的大量浪费。

近年来越来越多的研究人员意识这个问题的重要性，为了解神经网络的学习过程，Zeiler等^[50]提出了一种针对卷积神经网络的可视化方法。该方法通过对神经网络学习的特征进行可视化，为优化网络结构、提升预测的准确性提供了思路。

针对具体的条纹投影应用（如计算包裹相位、相位展开、高动态范围成像等），到底什么样的神经网络合适？尽管从前人相似工作中能找到网络结构设计的灵感，但是在神经网络后期的调试与优化过程中，如何调整超参数（如神经网络的类型，卷积神经网络中滤波器的尺寸，抽取特征的数量等）使得能够在自己的应用上表现出色仍是一个难以回答的问题。通过试错法进行超参的调整尽管有一定效果，但时间成本过高。此外，当神经网络的规模足够大时，想要快速地输出结果对计算平台的硬件也是一种考验。对于固定的服务器而言，这种影响相对较小。但是对于移动终端或者穿戴设备，如手机、平板、智能手表等，通常难以将规模过大的神经网络部署到这些设备上，而这时需要考虑对网络结构进行压缩。

令人欣喜的是，近年来自动化机器学习（AutoML）成为深度学习技术领域的一个研究热点。自动机器学习的目标就是使计算机自动地做出上述的决策。自动机器学习采用：超参数优化^[51]（Hyper-parameter Optimization）、元学习^[52]（Meta Learning）、神经网络架构搜索^[53]（Neural Architecture Search）等方式自动搜索理想网络结构与超参数。使用者只需提供训练数据，自动机器学习系统就能自动地决定最佳的训练方案。让不同领域的研究人员不必苦恼于学习各种机器学习的算法。

神经网络并非一个新概念，它实际上已具有几十年的历史。但是由于它是一种数据驱动的计算方法，几十年前的数据规模并未像今天一样地井喷式增长。因此当前迅速发展的互联网时代积累下的数据与算力释放了深度学习神经网络的潜力。

但就当前而言，对于条纹投影技术领域，训练数据的大规模获取与正确标注仍需要耗费大量的人力和物力成本。加之公开的数据集稀少，这都增加了深度学习技术的实施难度。尽管采用仿真的方式获取数据集可在一定程度上降低训练数据采集过程中的成本。但是仿真数据受制于有限的预设参数，它并不能完全等于真实数据。而深度学习的强大能力就在于学习与发掘输入数据与输出数据之间的潜在联系。因此，如何快速获得准确可靠的训练数据是提高深度学习技术在条纹投影技术领域应用效率的一个重要问题。值得注意的是迁移学习将是解决这一问题的一个潜在方案。迁移学习^[54]的初衷是节省人工标注样本的时间，让模型可以通过已有的标记数据向未标记数据迁移，从而训练出适用于未标记数据的运算模型。

泛化能力评价的是一个神经网络在完成训练后，在处理“从未遇见过”的输入数据时的表现。对于传统的条纹投影方法而已，得益于构建的数学模型普适通用，对于满足朗伯体假设条件的所有测量对象，均可获得较为理想的三维成像。但是如前所述，深度学习技术是以数据为导向的算法，它依赖于大量的训练数据为其良好的表现提供基础。因此当训练数据的类型较少时，深度神经网络往往难以抽取以及学习有效的图像特征映射。为了提升神经网络在处理全新场景的能力，大规模的训练数据通常是必不可少的。

但是，笔者认为关于神经网络的泛化能力应该能够一分为二的看待。这就像是“通才”与“专才”。“通才”掌握知识全面，但深度有所不足，且往往需要大量的时间累积以获得丰富的知识储备。而“专才”尽管只专注于部分领域，但能够做到精益求精。其实“通才”与“专才”都是社会发展或不可或缺的。

因此，对于条纹投影的应用而言，如果拟研制系统设计的潜在对象类型本身就较为单一，通过单方面地增加相同类型的训练数据就应该能对其性能提高发挥积极的效用。同时还能节省设备的开发周期，有利于专用系统的快速研发。笔者认为一切从实际出发，具体问题具体分析，才能最大限度地发挥深度学习技术的特长。

深度学习的强大能力源于大量的训练数据支撑与驱动。因此本质上来说，这样的人工智能只能机械式的学习而缺乏推理能力。图灵奖得主、贝叶斯网络之父Judea Pearl曾指出当前的深度学习“不过只是曲线拟合”。以条纹投影中的条纹分析为例，根据第二节中所述方法，目前基本的策略是两步走：先利用深度学习技术学习求解某项中间变量（比如条纹的实部信息与虚部信息），然后再将中间变量代入反正切函数计算最终的包裹相位。由于缺乏推理能力，神经网络不知道包裹相位具有不连续空间跳变性质的先验知识，难以训练神经网络直接计算包裹相位。

基于物理模型的算法仍是当今世界科技的核心。尽管在许多任务中，数据驱动模型算法表现已优于物理驱动模型算法，但“数据驱动”的可解释性仍是个挑战。对于条纹投影的应用，我们认为需要向当前以“数据驱动”的神经网络引入“物理模型”。只有把数据和物理结合起来，综合运用数据与物理两个世界的优势，才能更全面地揭示出问题的本质。

文中回顾并讨论了近年来基于深度学习的条纹投影三维成像技术的研究现状。尽管这一研究方向才刚起步，但对于已经经历了几十年发展历程的条纹投影技术而言，这无疑是一个具有强大潜力的新增长点。总的来说，在深度学习技术的辅助下，将条纹投影技术放在以“数据驱动”的神经网络模型中重新考虑后，笔者发现的优势包括：

（1）相位测量效率的提升 当前面向运动物体的快速三维成像是条纹投影技术的一个热点研究方向。尽管通过补偿的方式可有效去除由物体运动引起的运动误差，但当物体运动过快时，这类补偿算法仍难以发挥期待的效果。而深度学习技术仅采用单幅光栅图像即可准确恢复物体的相位信息，从而减少了三维图像重建所需的条纹图像数量，提高了成像的效率。结合多视角几何理论，该方法有望成为快速三维成像的一种理想手段。

（2）相位测量精度的提高 作为条纹投影技术而言，三维成像质量的优劣直接取决于相位质量的好坏。对于用于求解相位信息的神经网络，当其经过适当的训练，其计算得到的包裹相位比传统的单幅条纹分析方法获得的相位信息更加准确，有效降低相位误差，相位解调精度已接近相移法。

（3）成像稳定性的提升 将深度学习应用于相位展开，无论是空域展开还是时域展开，经过深度神经网络的处理，原始包裹相位中的噪声均得到了较好的抑制。这使得即使在信噪比不理想的情况下，依然能获得准确的去包裹相位。此外，将深度学习技术直接应用于条纹图像的去噪，也能较好地去除图像中的噪声。

尽管在深度学习的辅助下，条纹投影三维成像取得新的研究进展。但是人们依然需要意识到，深度学习技术目前还无法做到真正的人工智能，这其中还有很长的路要走。为了能够更好地将深度学习技术应用于条纹投影三维成像技术的研究之中，首先需要明白“深度学习到底学到了什么？”。由于难以把握神经网络的推演机理，为了提升神经网络的性能，大部分人能做的只有试错。因此急需理解神经网络到底是如何思考我们为其布置的任务，进而找到优化神经网络的有效线索，避免无明确方向的试错造成的时间浪费。

在不久的将来，借助于自动机器学习，人们完全可以期待深度神经网络根据自己部署的需求，通过自身的迭代优化，自动地给出最佳的网络架构设计与优化。自动的机器学习将进一步降低深度技术应用的门槛，为条纹投影技术研究与应用的深度定制提供高效可靠的方案。

对于基于深度学习的条纹投影技术研究而言，目前的训练数据基本都需要实地采集与标注，这需要耗费大量的人力和物力成本。在仿真数据尚不能完全代替实拍数据的前提下，基于少量样本的迁移学习将是提高研究效率的一个有效手段。同时，为了保障训练的神经网络能够处理各种不同类型的物体，需要在训练过程中尽可能多的让神经网络接触不同的物体，以提升其泛化能力。但是对于某些专用设备的研制，我们也许能够反向运用这种泛化能力，利用少量的同类样本训练研究针对特定样本的专用算法。最后，为进一步提升神经网络的性能，可在神经网络模型的构建或者迭代过程中加入“物理驱动”的引擎，这样有利于神经网络更为全面地认识问题的本质。

综上所述，条纹投影三维成像技术是一个极具发展前景的三维图像获取技术。在人工智能的辅助下，基于深度学习的条纹投影三维成像在相位测量效率、相位测量精度与三维成像稳定性等方面得到显著提升。这将推动条纹投影技术的进一步快速发展，以及带动该技术在更多领域的深入应用。