-
利用各种方法实现极性气体分子的取向和定向,不但可以实现相干操控分子转动和振动的运动状态、揭示原子与分子运动的基本量子规律,而且可以提升激光高次谐波产生效率、提高原子离化率、控制化学反应产物和速率[1-2]。因此,实现和优化分子取向和定向的研究是国际上原子分子光学领域一个极为活跃的研究课题。使用超短激光脉冲和太赫兹 (terahertz) 脉冲对气体分子进行取向和定向[3-5],不但打破了原有绝热过程的限制,实现分子非绝热过程的取向和定向,并且实现了分子在无外场(field-free)下的取向和定向,拓展了量子操控原子分子状态的技术途径,从而能够便于利用量子状态可控的分子介质,大大推动了分子超快动力学过程的基础研究和应用研究。
极性气体分子在无任何外电场作用下,其系综的分布为随机分布,即大量分子的轴向空间分布各向均匀,气体介质表现为各向同性。利用外加静电场[3]、超短激光脉冲[5]或者强场太赫兹脉冲[6]等技术产生分子取向或定向后,气体分子轴向具有一定规律的空间分布,以分子轴向与外电场方向之间的夹角为θ,引入描述分子转动状态的取向度物理参数《cos2θ》和定向度物理参数《cosθ》来表征分子系综取向和定向效果的强弱[1,7]。二者均为气体分子系综对单个分子量子状态的统计效果,能够很好地连接单个气体分子量子状态和气体介质整体的宏观性质。
为了更好地获得分子取向或者定向的信息,需要准确地测量取向度和定向度。目前分子取向的测量方法主要有两种,一种是库伦爆炸技术[8-9],一种是弱场偏振探测技术[10]。前者用较强的探测光电离取向后的气体分子,利用静电场对带电粒子进行加速使得不同荷质比的带电粒子飞行固定距离的时间存在差异,从时间上得到不同带电粒子的分布。这种方法的弊端是强探测光把取向后的分子电离,难以对其进行后续应用。弱场偏振探测技术利用取向后的分子表现出的双折射性使微弱探测光的偏振态发生改变,由探测光的偏振改变量得到气体分子的取向度。这种测量不是直接测量出分子取向的结果,在测量中不会改变分子量子状态和分子系综的宏观性质,有利于取向后的分子进一步开展其他应用。特别是无外场分子取向和定向的成功实现,更需要一种不改变分子状态的探测技术,以便观测分子状态无外场的时间演化。因此,弱场偏振探测技术在分子取向和定向中的应用显得愈发重要。
随着对弱场偏振探测技术的广泛使用和深入发展,以其为基础逐步进行了一定的改善措施。文中主要介绍弱场偏振探测技术和以其为基础的改善技术——平衡弱场偏振探测技术的物理机制、探测原理和具体实验方案,利用泰勒级数近似方法系统分析、比较了这两种技术的灵敏度,讨论了其测量过程中的噪声来源和影响,并详细比较了二者的特点,从而能够为搭建分子取向的探测系统提供定性参考。
-
对于极性分子,可视为能转动的条状长棒,其在常态下的分子轴向为随机分布,分子轴向的指向为各向同向,从而使得气体介质的折射率也是各向同向。当极化张量为α的分子处于电场E中,该分子具有偶极势能:
$$ {{U}} = - \frac{1}{2}{{E}} \cdot {{\alpha }} \cdot {{E}} = - \frac{1}{2}{{{\alpha }}_\parallel }{{E}}_\parallel ^2 - \frac{1}{2}{{{\alpha }}_ \bot }{{E}}_ \bot ^2 $$ (1) 这里
${{\rm{\alpha }}_\parallel }$ 和${{{\alpha }}_ \bot }$ 分别为极化率沿分子主轴方向和垂直分子主轴方向上的分量,${{{E}}_\parallel }$ 和${{{E}}_ \bot }$ 分别为电场在这两个方向的分量。令分子主轴方向与电场的夹角为θ,上式可简化为:$$ {{U}}\left( {\rm{\theta }} \right)\!=\!- \frac{1}{2}{{{\alpha }}_\parallel }{{{E}}^2}{\rm{co}}{{\rm{s}}^2}{\rm{\theta }} - \frac{1}{2}{{{\alpha }}_ \bot }{{{E}}^2}{\rm{si}}{{\rm{n}}^2}{\rm{\theta }}\!=\!- \frac{1}{2}{{{E}}^2}\left( {{{{\alpha }}_ \bot }\!+\!\Delta {\rm{\alpha co}}{{\rm{s}}^2}{\rm{\theta }}} \right) $$ (2) 引入参量
$\Delta {\rm{\alpha }} = {{\rm{\alpha }}_\parallel } - {{\rm{\alpha }}_ \bot }$ ,即分子极化率在分子主轴方向和垂直分子主轴方向的差值。参量$\Delta {\rm{\alpha }}$ 为表征气体分子光学性质各向异性的重要参数,不同的分子,该参量有所不同。公式(2)表明,在外电场作用下,极性分子产生一个作用势,由于分子极化率在外电场平行方向和垂直方向的两个分量不同,该作用势对分子将产生这两个方向的力矩${{{M}}_\parallel } = \dfrac{1}{2}{{{\alpha }}_\parallel }{{{E}}^2}{\rm{sin}}2{{\theta }}$ 和${{{M}}_ \bot } = $ $\dfrac{1}{2}{{\rm{\alpha }}_ \bot }{{{E}}^2}{\rm{sin}}2{\rm{\theta }} $ ,并且由于分子极化率α的各向异性,分子的净力矩不为零。从而使得分子在净力矩${{{M}}_{{\rm{net}}}} = {{{M}}_\parallel } - {{{M}}_ \bot }$ 作用下朝着势能U(θ)变小的方向转动。由公式(2)可以看出,当分子主轴与外电场夹角为0或者π时,势能达到最小值,此时分子主轴与电场方向保持一致,分子主轴便有了确定的取向方向。由于气体分子系综的宏观物理量是各个分子的微观状态的加权统计平均值,即加权统计平均值
$ \ll {\rm{co}}{{\rm{s}}^2}{\rm{\theta }} \gg $ 反应了作为介质的气体的取向问题,其值大小的改变导致了气体介质相关物理参数的改变,而这些物理参数的改变导致了基于分子取向的气体分子整体的物理效应和应用。在热平衡状态下,气体系综的统计平均值
$ {\ll\rm{co}}{{\rm{s}}^2}{\rm{\theta }} \gg$ 可表示为:$$ \ll {\rm{co}}{{\rm{s}}^2}{\rm{\theta }} \gg = \frac{{ \smallint {\rm{d{\varOmega} co}}{{\rm{s}}^2}{\rm{\theta exp}}\left[ { - {{U}}\left( {\rm{\theta }} \right)/{{kT}}} \right]}}{{ \smallint {\rm{d\varOmega exp}}\left[ { - {{U}}\left( {\rm{\theta }} \right)/{{kT}}} \right]}} $$ (3) 式中:
${\rm{d\varOmega }} = 2{\rm{\pi sin\theta d\theta }}$ 为对立体角Ω的积分。无外加电场作用下,${{U}}\left( {\rm{\theta }} \right) = 0$ ,上式可得到积分值:$$ \ll {\rm{co}}{{\rm{s}}^2}{\rm{\theta}} \gg = \frac{{\mathop \smallint \nolimits_0^{\text{π}}} {\rm{co}}{{\rm{s}}^2}{\rm{\theta sin\theta d\theta }}}{{\mathop \smallint \nolimits_0^{\text{π}}} {\rm{sin\theta d\theta }}} = \frac{1}{3}$$ (4) 当使用某种技术手段使得分子主轴方向和入射电场方向平行时,气体系综的统计平均值
$ \ll {\rm{co}}{{\rm{s}}^2}{\rm{\theta }} \gg > \dfrac{1}{3}$ ,此时称为平行取向,${\rm{}} \ll {\rm{co}}{{\rm{s}}^2}{\rm{\theta }} \gg = 1$ 为完全平行取向;当分子主轴垂直电场方向时,$ \ll {\rm{co}}{{\rm{s}}^2}{\rm{\theta }} \gg < \dfrac{1}{3}$ ,一般称为垂直取向,$ \ll {\rm{co}}{{\rm{s}}^2}{\rm{\theta }} \gg = 0$ 为完全垂直取向。简言之,气体分子取向即大量无序极性气体分子的主轴方向平行或者垂直某一方向。如果分子“头-尾”方向固定朝向某一方向,则称为分子定向。目前,已有一些基于超短激光脉冲技术[3-5,11]和太赫兹脉冲技术的方法使得分子由绝热过程完成无外场取向和定向[6, 12-14],气体分子系综与超短激光脉冲或者太赫兹脉冲作用后,分子转动状态成为有周期性的、有统一规律的运动,从而达到无外场的效果。无外场分子取向和定向的实现,为其进一步应用提供了便利。
当大量气体分子的轴向由随机方向变成有规律的方向,气体分子微观性质进而会改变气体系综的宏观性质,并产生可观测的物理量的变化。气体介质的折射率与宏观极化率的关系可以表示为
$n = \sqrt {1 + {\rm{\chi }}} $ ,由单分子极化率${\bf{\alpha }}$ 可知气体介质的折射率为:$$ n = \sqrt {1 + N\alpha } = \sqrt {1 + N \left[ {{{\rm{\alpha }}_ \bot } + \left( {{{\rm{\alpha }}_\parallel } - {{\rm{\alpha }}_ \bot }} \right){\rm{co}}{{\rm{s}}^2}{\rm{\theta }}} \right]} $$ (5) 式中:N为气体分子数密度。利用级数展开取一级近似,上式可近似为:
$$ n \approx 1 + \frac{N}{2}\left( {{{\rm{\alpha }}_ \bot } + \Delta {\rm{\alpha co}}{{\rm{s}}^2}{\rm{\theta }}} \right) $$ (6) 当分子状态为随机取向时,
$ \ll {\rm{co}}{{\rm{s}}^2}{\rm{\theta }} \gg = \dfrac{1}{3}$ ,则折射率为${n_0} \approx 1 + \dfrac{N}{2}\left( {{{\rm{\alpha }}_ \bot } + \dfrac{1}{3}\Delta {\rm{\alpha }}} \right)$ 。因此,对于有一定取向分布的气体分子介质,其折射率变化为:$$ \Delta n = n - {n_0} = \frac{{N \Delta {\rm{\alpha }}}}{2}\left( { \ll {\rm{co}}{{\rm{s}}^2}{\rm{\theta }} \gg - \frac{1}{3}} \right) $$ (7) 公式(7)说明当分子取向后,随后而来的探测激光,其偏振方向与泵浦激光脉冲偏振方向平行时,探测光的折射率与分子随机分布状况下的相比,折射率增大了Δn。当探测光的偏振与泵浦光的偏振垂直时,此时分子主轴与探测光偏振方向为
${{\rm{\theta }}_ \bot }$ ,有$\ll {\rm{co}}{{\rm{s}}^2}{{\rm{\theta }}_ \bot } \gg = $ $ \dfrac{1}{2}\left( {1 - \ll {\rm{co}}{{\rm{s}}^2}{\rm{\theta }} \gg } \right)$ ,此时探测光的折射率变化为:$$ \Delta n' = n' - {n_0} = \frac{{N\Delta {\rm{\alpha }}}}{2}\left( { \ll {{\cos }^2}{{\rm{\theta }}_ \bot } \gg - \frac{1}{3}} \right) = - \frac{{\Delta {{n}}}}{2} $$ (8) 公式(8)表明探测光与泵浦光偏振垂直时,探测光的折射率改变是探测光与泵浦光偏振平行时的一半;分子取向引起的气体介质的双折射效应,与
$\left( { \ll {\rm{co}}{{\rm{s}}^2}{\rm{\theta }} \gg - \dfrac{1}{3}} \right)$ 成正比。因此,通过光学手段测出气体介质的折射率变化量,即可间接获得气体分子的取向度。 -
弱场偏振技术即利用微弱的探测光结合光学偏振元件和光电器件来探测气体分子的取向度。下面对其探测原理和光学系统构成进行详细介绍和讨论。
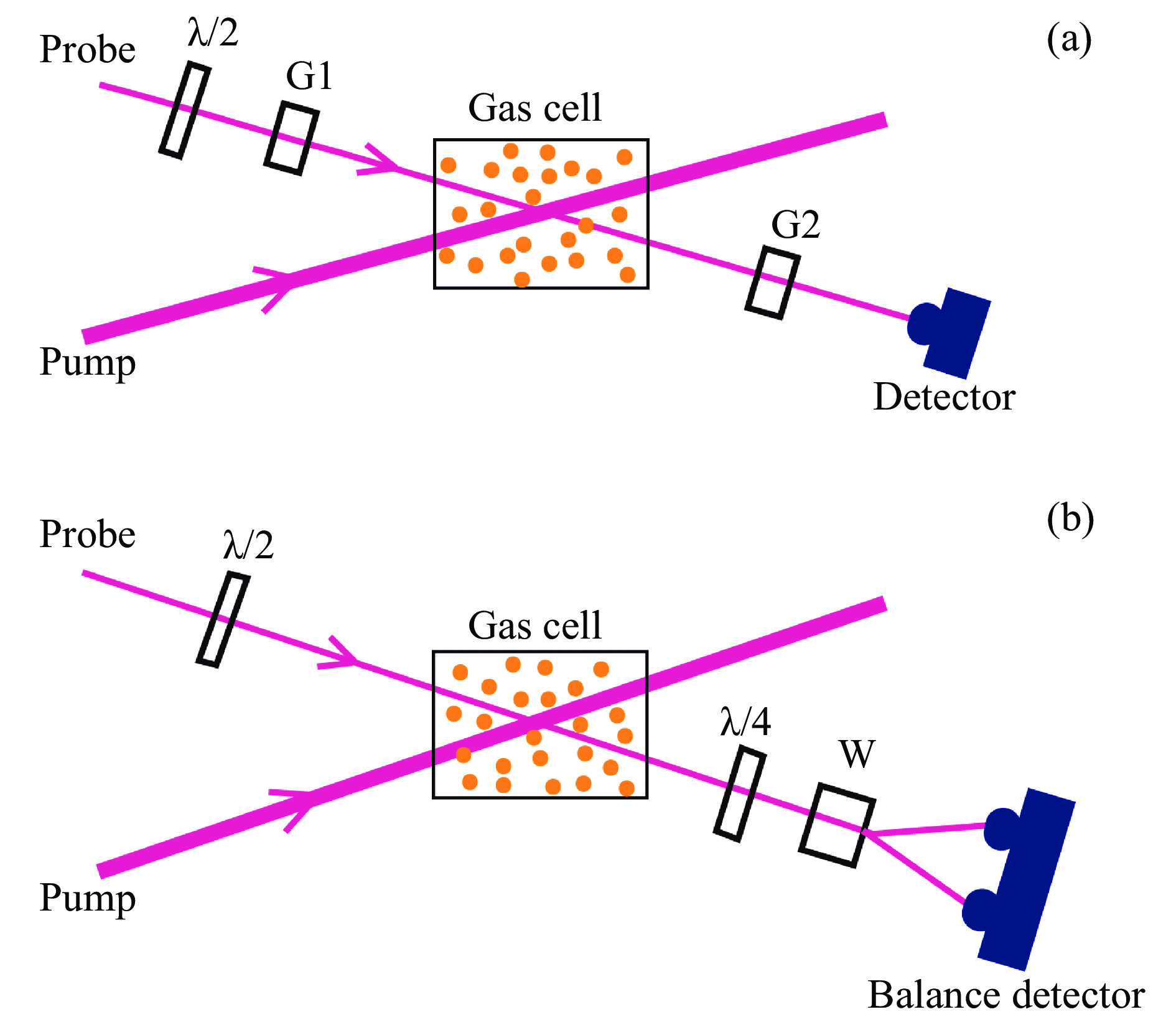
利用光学技术控制气体分子的转动态,从而实现分子取向,此时分子主轴有一个固定方向。使得较弱的探测光透射该气体分子系综,则可以利用测量探测光的偏振态的改变获得分子取向度。此即弱场偏振的含义。图1(a)为传统的弱场偏振探测技术的光路示意图,该技术中用一个二分之一波片改变探测光的偏振方向,使其偏振方向和泵浦光的偏振方向成45°,而后依次穿过第一个格兰棱镜G1、待测的气体介质和第二个格兰棱镜G2,并使探测光入射到光电探测器。两个格兰棱镜的消光方向为正交。当气体分子无取向时,即气体介质表现为各向同性,探测光不能穿过两个正交的格兰棱镜,因而光电探测器的信号为零。当气体分子获得一定取向从而获得双折射性质时,穿过第一个格兰棱镜的探测光偏振态发生改变,从而有部分光透射过第二个格兰棱镜,并被光电探测器探测到。探测光足够弱从而不会改变待测的气体分子状态,所以光电探测器所探测到的信号大小与
$\left( { \ll {\rm{co}}{{\rm{s}}^2}{\rm{\theta }} \gg - \dfrac{1}{3}} \right)$ 成正比[9]。对于利用超短激光脉冲和太赫兹脉冲无外场技术实现的取向分子,即泵浦激光脉冲和太赫兹脉冲完成对分子状态的激励后传播离开,分子状态依然能保持取向度周期性重现,改变探测光和泵浦光之间的延迟,这种分子取向的周期性重现能够完全探测出来。
图 1 (a)弱场偏振探测技术及(b)平衡弱场偏振探测技术实验原理图
Figure 1. Experimental setup schematics of (a) weak field polarization detection technique and (b) balanced weak field polarization detection technique
平衡弱场偏振技术是对上述探测技术的改进,其光路示意图如图1(b)所示[15]。即仍用一个二分之一波片对探测光的偏振方向进行控制,使探测和泵浦光的偏振成45°,而后探测光依次穿过气体介质、四分之一波片和沃拉斯顿棱镜,探测光经过沃拉斯顿棱镜分光后入射到光电平衡探测器。当气体分子无取向时,气体介质表现为各向同性,调节四分之一波片使得穿过沃拉斯顿棱镜的两束光的光强相同,因此光电平衡探测器的信号为零。当气体分子获得一定的取向度,气体介质获得双折射特性时,由沃拉斯顿棱镜分出的两束光的光强发生变化,二者产生的光电信号之差不再是零,而是与分子取向引起的折射率变化成正比,即与分子取向度
$\left( { \ll {\rm{co}}{{\rm{s}}^2}{\rm{\theta }} \gg - \dfrac{1}{3}} \right)$ 成正比[16-17]。上述两种探测技术均采用较弱的探测光。改变探测光与泵浦光的时间延迟,既可获得气体分子取向度的时间演化信号。由于这两种探测技术光路略有不同,二者各自的噪声和探测灵敏度略有不同。
-
下面对这两种探测技术的灵敏度和噪声进行分析和讨论。对于弱场偏振探测技术,气体分子无取向分布时表现为各向同性,因而其折射率为圆分布;当分子有一定的取向分布时,其折射率为椭圆分布,这里定义椭圆的长轴方向为分子取向的方向,探测光偏振方向和第一个偏振片G1透射方向相同,第二个偏振片G2偏振方向与G1垂直。图2为折射率变化分布和探测光偏振示意图。设探测光电场为E0,则其在x、y两个方向的分量为:

图 2 气体取向分布引起的折射率的变化和入射的探测光电场偏振示意图
Figure 2. Schematic of the change of refractive index, the polarization of laser field and the directions of the polarizers
$$ \left\{ {\begin{split} & {{E_x} = {E_0}{\rm{cos}}\left[ {{\rm{\theta }} + {{\varGamma }}\left( {\Delta {{t}}} \right)} \right]}\\ & {{E_y} = {E_0}{\rm{sin}}\theta } \end{split}} \right. $$ (9) 式中:θ为入射激光电场和折射率椭圆长轴的夹角;
$\varGamma \left( {\Delta {{t}}} \right)$ 为取向后分子折射率的改变对激光引入的相位差;$\Delta {{t}}$ 表示Γ是泵浦脉冲和探测光脉冲之间时间延迟量的函数。实际操作中,Δt一般通过改变泵浦光和探测光的量程来实现二者之间的时间延迟。当气体状态分布为随机分布,即Γ为零,此时在弱场偏振探测中,由于两个偏振片的偏振方向垂直(图2中G1和G2),因此光电探测器信号为零。当使用一定技术手段使得气体分子获得一定的取向分布,气体介质对探测光表现出双折射性,此时折射率为椭圆分布,并且对入射的探测光引入额外的相位Γ,使得x和y方向的探测光分量发生变化。从而使得二者的矢量和与原来的方向发生偏差,有少许探测光透过两个正交的偏振片,并被光电探测器探测到。取
$\theta= {45^ \circ }$ ,令能够透射出偏振片G2的探测光电场为${E_{\rm{G2}}}$ 。由于气体介质折射率改变量为小量,使得Γ为小量。根据三角函数基础知识,代入公式(9)并采用泰勒级数展开,取一级近似得到:$$ {E_{\rm{G2}}} = {E_x}{\rm{sin\theta }} - {E_y}\cos\theta \approx - \frac{1}{2}{E_0}\varGamma $$ (10) 因此光电探测器的光电信号大小为:
$$ {I_{{\rm{singal}}}} \propto {\left( {{E_{\rm{G2}}}} \right)^2} \approx \frac{1}{4}E_0^2{\varGamma ^2} $$ (11) 公式(11)表明,在较弱的探测光和气体分子具有较小的取向度时,光电探测器获得的信号与气体介质折射率改变量引入的相位差平方成正比。
平衡弱场偏振探测方法采用四分之一波片、沃拉斯顿棱镜和一个光电平衡探测器对分子取向引起的气体介质折射率的改变进行测量。其探测激光的偏振方向在前端用一个二分之一波片进行控制,而后探测激光入射到待测气体,并通过四分之一波片引入固定相差。气体介质的折射率分布和探测光偏振与图2相同。探测激光经过沃拉斯顿棱镜分光后,两个偏振方向的电场分别为:
$$ \left\{ {\begin{split} & {{{{E}}_{{x}}} = {{{E}}_0}{\rm{cos}}\left[ {{\rm{\theta }} + {{\rm{\varGamma }}_0} + {\rm{\varGamma }}\left( {\Delta {{t}}} \right)} \right]}\\ & {{{{E}}_{{y}}} = {{{E}}_0}{\rm{sin}}\left[ {{\rm{\theta }} + {{\rm{\varGamma }}_0}} \right]} \end{split}} \right. $$ (12) 式中:
${{\rm{\varGamma }}_0}$ 为四分之一波片引入的相位;$\varGamma \left( {\Delta t} \right)$ 为气体分子取向后双折射效应引入的相位。光电平衡探测器测到的信号为两个偏振方向的光电信号之差,即$I_{{\rm{singal}}}^{{p}} \propto {{E}}_{{x}}^2 - {{E}}_{{y}}^2$ 。注意到该技术中的二分之一波片是用来调整探测激光的偏振方向,并结合四分之一波片调整探测光的偏振分布,使其能够在通过沃拉斯顿棱镜后获得偏振平衡分光。二者之和引入的相位差为${\rm{\theta }} + {{{\varGamma }}_0} = {45^ \circ }$ 。若气体介质为各向同性,即Γ=0,经过沃拉斯顿分光后,x和y方向二者光强相同,即${{{E}}_{{x}}} = {{{E}}_{{y}}}$ ,光电平衡探测器信号为零。当气体分子获得一定取向,气体介质表现出双折射性时,${\rm{\varGamma }} \ne 0$ ,所以${{{E}}_{{x}}} \ne {{{E}}_{{y}}}$ 。此时,由三角函数基础知识和Γ的泰勒级数近似方法,取Γ的一级近似,由公式(12)可得到光电平衡探测器的光电信号为:$$ I_{{\rm{singal}}}^{p} \propto {E}_{x}^2 - {E}_{y}^2 \approx - {E}_0^2{\rm{\varGamma }} $$ (13) 该式表明光电平衡探测器的光电信号与分子取向后形成的双折射性带入的相位差成正比,比例系数由探测光的光强决定。
由公式(11)与(13)的差别,即可获得在相同的外界情况下,传统的弱场偏振探测技术和平衡弱场偏振探测技术的灵敏度差别。公式(11)表明光电探测信号为相位差的二次函数,而公式(13)表明平衡光电探测信号为相位差的正比例函数,二者的系数均与探测光强相关。对于分子取向度较小时且探测光强相同情况下,作为光电信号函数变量的相位差Γ也较小,此时相位差的正比例函数大于其二次函数,因此平衡光电探测器的光电信号强于单个的光电探测器的信号。所以,在不考虑实验成本且获得的分子取向度较小的前提下,平衡弱场偏振探测技术比传统的弱场偏振探测技术更为灵敏。平衡弱场偏振探测技术应用了光学差分探测的原理,对弱信号的探测较为灵敏,与原子陀螺微弱光信号的检测方法有一定类似[18]。
在弱场偏振探测技术和平衡弱场偏振探测技术中,探测的噪声主要有激光系统的涨落使得探测光脉冲能量涨落引入的噪声Nlaser、偏振棱镜消光比引入的噪声NP、探测器引入的噪声ND。由于泵浦激光脉冲能量和气体分子量子态的改变不是线性关系,这里忽略泵浦光能量涨落使得气体分子量子态改变的涨落引起的噪声,从而可以分析由于探测光路不同而导致的探测噪声的不同。因此,弱场偏振探测技术和平衡弱场偏振探测技术总的噪声可分别表示为:
$$ {N_{w}} = \sqrt {{N}_{{\rm{laser}}}^2 + 2{N}_{P}^2 + {N}_{D}^2} $$ (14) $$ N_{BW} = \sqrt {N_{{\rm{laser}}}^2 + {N}_{{P}}^2 + {N}_{D}^2} $$ (15) 在平衡弱场偏振探测技术中,采用平衡探测器对沃拉斯顿棱镜分光后的两束不同偏振方向的光进行探测并得到这两束光能量差的改变值,激光脉冲能量的涨落使得这两束光同时进行涨落,因而二者能量差的改变值消除了激光能量的涨落,因此能够把激光脉冲能量涨落引入的噪声消除。因此公式(15)可简化为:
$$ N_{BW} = \sqrt {{N_P^2} + {N}_{D}^2} $$ (16) 比较公式(14)和(16)可知,平衡弱场偏振探测技术的噪声来源比传统的弱场偏振探测技术噪声来源少了激光脉冲能量涨落引起的噪声。在实际使用中,若激光能量涨落较大(即脉冲能量不稳定或者激光平均功率不稳定),其引入探测技术的噪声远大于激光偏振片和探测器引入的噪声,则平衡弱场偏振探测技术远远优于传统的弱场平衡探测技术;若激光能量稳定性很好,其能量涨落较小,探测的噪声主要由于激光偏振片和探测器引入的噪声,则这两种探测技术的信噪比相接近,平衡弱场偏振探测技术略优于弱场偏振探测技术。
上述关于两种探测技术的灵敏度比较和噪声来源虽然仅是简单的定性讨论,但是本文给出的两种方法的物理图像较为清晰,该结果对于搭建实验系统、分析具体的实验结果具有较好的定性参考。后续工作将结合具体实验和数值计算定量分析、比较两种方法的灵敏度和噪声,从而验证文中定性分析的结果。
-
文中详细介绍了分子取向常用的探测方法−弱场偏振探测技术和平衡弱场偏振探测技术的探测原理和探测光路结构,详细比较了二者的异同,并对这两种探测方法的灵敏度和噪声来源进行了定性分析和比较。利用泰勒级数展开和一级近似发现,在取向度较小时前者的光电探测器的光电信号由气体分子取向后形成的双折射率对探测激光引入的相位差的平方决定,后者的光电信号由相位差决定。因此,对于取向度较小的气体介质和不考虑实验仪器代价的前提下,平衡弱场偏振探测技术更为灵敏。由于在该技术中用了两个光电探测器对探测激光两束偏振正交的分量进行差分探测,使得该技术可以消除激光脉冲能量涨落引起的探测噪声。因此,在激光脉冲能量涨落明显的情况下,平衡弱场探测技术有很好的优点。若激光脉冲能量涨落比较小,则二者引入的噪声比较接近。后续,将通过实验和数值计算对文中的定性分析进行更深一步的分析。总之,本项研究对于搭建用于探测分子取向的弱场偏振探测实验系统、理解该探测技术的灵敏度和噪声来源有很好的参考意义。
Qualitative analysis of the sensitivity and the noise of weak field polarization detection technique
-
摘要: 弱场偏振探测技术是分子取向探测技术的一种。该探测技术不会破坏无外场取向分子的量子状态从而便于取向后的分子进行各种实际应用,因此这种技术在分子取向的研究中运用较为广泛。详细介绍了弱场偏振探测技术和其改进技术——平衡弱场偏振探测技术的探测原理和实验系统组成,以泰勒级数为基础采用近似方法分析、比较了两种探测技术的灵敏度,探讨了二者的噪声来源和影响。研究发现,在分子取向度较小时,后者的灵敏度比前者较强;探测激光能量涨落较大时,后者的噪声明显低于前者;探测激光能量涨落可以忽略时,二者的噪声大小比较接近。Abstract: Weak field polarization detection technique is one of detection techniques of the molecular alignment. This method does not damage the quantum state of the field-free aligned molecules, thus it is convenient for the further applications of these aligned molecules. The principles and the experimental schematics of the weak field polarization technique, and its improvement-balanced weak field polarization detection technique were introduced in detail. Based on the Taylor series approximation, the sensitivity of these two techniques were analyzed and compared. The original noises of these two techniques were investigated as well. The study found that the sensitivity of the latter is higher than the former when the alignment degree of the molecules is lower. The noise of the latter is lower than the former when the fluctuation of the laser pulse energy is obvious. The noises of the two techniques are close when the fluctuation of the laser pulse energy can be ignored.
-
Key words:
- molecular alignment /
- weak field polarization /
- sensitivity /
- noise
-
-
[1] Stapelfeldt H, Seideman T. Colloquium: Aligning molecules with strong laser pulses [J]. Reviews of Modern Physics, 2003, 75(2): 543−557. doi: 10.1103/RevModPhys.75.543 [2] 罗嗣佐, 刘福春, 丁大军. 从随机到转向—分子转动动力学的超快调控[J]. 物理, 2015, 44(1): 9−15. doi: 10.7693/wl20150102 Luo Sizuo, Liu Fuchun, Ding Dajun. From random to oriented—ultrafast control of molecular rotation dynamics [J]. Physics, 2015, 44(1): 9−15. (in Chinese) doi: 10.7693/wl20150102 [3] Goban A, Minemoto S, Sakai H. Laser-field-free molecular orientation [J]. Physical Review Letters, 2008, 101(1): 013001. doi: 10.1103/PhysRevLett.101.013001 [4] Ghafur O, Rouzee A, Gijsbertsen A, et al. Impulsive orientation and alignment of quantum-state-selected NO molecules [J]. Nature Physics, 2009, 5: 289−293. doi: 10.1038/nphys1225 [5] Wu J, Zeng H P. Field-free molecular orientation control by two ultrashort dual-color laser pulses [J]. Physical Review A, 2010, 81(5): 053401. doi: 10.1103/PhysRevA.81.053401 [6] Fleischer S, Zhou Y, Field R W, et al. Molecular orientation and alignment by intense single-cycle THz pulses [J]. Physical Review Letters, 2011, 107(16): 163603. doi: 10.1103/PhysRevLett.107.163603 [7] Tehini R, Sugny D. Field-free molecular orientation by nonresonant and quasiresonant two-color laser pulses [J]. Physical Review A, 2008, 77(2): 023407. doi: 10.1103/PhysRevA.77.023407 [8] Rosca-Pruna F, Vrakking M J. Experimental observation of revival structures in picoseconds laser-induced alignment of I2 [J]. Physical Review Letters, 2001, 87(15): 153902. doi: 10.1103/PhysRevLett.87.153902 [9] Dooley P W, Litvinyuk I V, Lee K F, et al. Direct imaging of rotational wave-packet dynamics of diatomic molecules [J]. Physical Review A, 2003, 68(2): 023406. doi: 10.1103/PhysRevA.68.023406 [10] Renard V, Renard M, Guerin S, et al. Postpulse molecular alignment measured by a weak field polarization technique [J]. Physical Review Letters, 2003, 90(15): 153601. doi: 10.1103/PhysRevLett.90.153601 [11] De S, Znakovskaya I, Ray D, et al. Field-free orientation of CO molecules by femtosecond two-color laser fields [J]. Physical Review Letters, 2009, 103(15): 153002. doi: 10.1103/PhysRevLett.103.153002 [12] Kitano K, Ishii N, Kanai T, et al. Selecting rotational two-level coherence in polar molecules by double terahertz pulses [J]. Physical Review A, 2014, 90(4): 041402(R). doi: 10.1103/PhysRevA.90.041402 [13] Liu Y, Li J, Yu J, et al. Field-free molecular orientation by two-color shaped laser pulse together with time-delayed THz laser pulse [J]. Laser Physics Letters, 2013, 10(7): 076001. doi: 10.1088/1612-2011/10/7/076001 [14] 杨明惠, 金琪, 刘劲松, 等. 飞秒激光结合啁啾太赫兹脉冲控制CO分子取向[J]. 激光技术, 2015, 39(6): 735−740. doi: 10.7510/jgjs.issn.1001-3806.2015.06.001 Yang Minghui, Jin Qi, Liu Jinsong, et al. CO molecular orientation controlled by combination of chirped THz pulse and femtosecond laser pulse [J]. Laser Technology, 2015, 39(6): 735−740. (in Chinese) doi: 10.7510/jgjs.issn.1001-3806.2015.06.001 [15] Peng P, Bai Y, Li N, et al. Measurement of field-free molecular alignment by balanced weak field polarization technique [J]. AIP Advances, 2015, 5(12): 127205. doi: 10.1063/1.4937476 [16] Lavorel B, Babilotte P, Karras G, et al. Measurement of dichroism in aligned molecules [J]. Physical Review A, 2016, 94(4): 043422. doi: 10.1103/PhysRevA.94.043422 [17] Xu N, Wu C, Gao Y, et al. Measurement of the field-free alignment of diatomic molecules [J]. Journal of Physical Chemistry A, 2008, 112(4): 612−617. doi: 10.1021/jp075728h [18] 王婧, 周斌权, 吴文峰, 等. 基于自动消偏的原子陀螺微弱光信号检测方法[J]. 红外与激光工程, 2018, 47(8): 0817004. doi: 10.3788/IRLA201847.0817004 Wang Jing, Zhou Binquan, Wu Wenfeng, et al. Weak light signal detection method for atomic gyroscope based on automatic zeroing of the bias [J]. Infrared and Laser Engineering, 2018, 47(8): 0817004. (in Chinese) doi: 10.3788/IRLA201847.0817004 -






 下载:
下载: