-
在最近的科研研究和工业应用中,单点激光测距仪[1-3]和成像相机的集成运用,成为工业机器人等领域的研究焦点[4-5]。单点激光测距仪尺寸小巧、成本低廉,以其高精度深度提取能力,非常适合手持设备和轻便机器人平台兼容应用。但是传统基于单目相机的深度提取,其在光轴方向的精度不高,只能借助外部传感器的融合来改进其深度提取精度不高的缺点,因此,利用这两者的融合能够很好取长补短,发挥各自的优势。但是对于这两者的融合,标定其外部参数就显得很有意义,这有利于两者之间信息的融合,能够使这两种组合在工业应用领域发挥更大的优势。
对于激光测距仪与相机外参标定研究,已有很多学者进行研究。但是绝大多数都是基于二维或者三维激光测距仪的标定,因为二维或者三维激光测距仪能够提供的信息更多,不仅包括距离信息,还包括角度信息,能够为建立标定方程提供更多的参数和有用信息。
二维或三维激光测距仪可同时测量多个点,并已广泛应用于机器人[6-8]和巡航。然而,这些多点激光测距仪非常昂贵且笨重,从而限制了它们在手持或小型设备中的广泛应用。因此,一些研究人员研究了人们更可接受的单点激光测距仪。而且近年来,单点激光测距仪经常被组装在一些测量装置上,从而给这些装置测量物体参数时带来了很多便利。比如Patel[4]和Wither[5]等人提出利用单点激光测距仪在他们的增强现实系统中。近些年,单点激光测距仪进一步的微型化,移动设备中可以很容易地发现装备单点激光测距仪的模型[6],这些设备为将来广泛的应用推广开辟了新的机会,因此需要一个由单点激光测距仪和相机组成的系统的简单而且准确的标定过程。
文献中可以查阅到很多关于多点激光测距仪和相机的标定方法。Zhang和Pless[9]的一种广为人知的标定方法是在射影线商标定相机的固有参数和激光测距仪相对相机的位姿参数。另外Hebert[10]开发了一个快速简单的软件,可以校准三维激光测距仪与相机的外部参数和相机的内参。Vasconcelos[6]等人介绍了一种新的标定方法,该方法需要至少三个捕获的平面姿态用于约束方程的建立,但是他们只专注于相机和激光测距仪外部参数的标定,对于相机的内参则认为是事先标定好的。
与二维或者三维激光测距仪外参标定不同,由于激光在图像中被限制在单个点上,无法建立激光测距仪坐标系与相机坐标系之间的转换关系,因此对单点激光测距仪和相机相对姿态的标定需要一种完全不同的方法。目前能够查询到的单点激光测距仪与相机外参的标定研究只有浙江大学的熊蓉,他的做法是先提取激光测距仪点云数据边缘轮廓和相机图像的边缘轮廓,建立点云数据边缘的概率分布,然后最小化两个分布的KL距离,求得激光测距仪和相机的相对位姿参数。虽然该方法能够标定得到位姿参数,但是时间消耗较多,原理较为复杂。因此,文中提出了两种方法来解决标定单点激光测距仪和相机的外部参数这一问题。最终的实验结果表明我们的方法是有效和准确的。
-
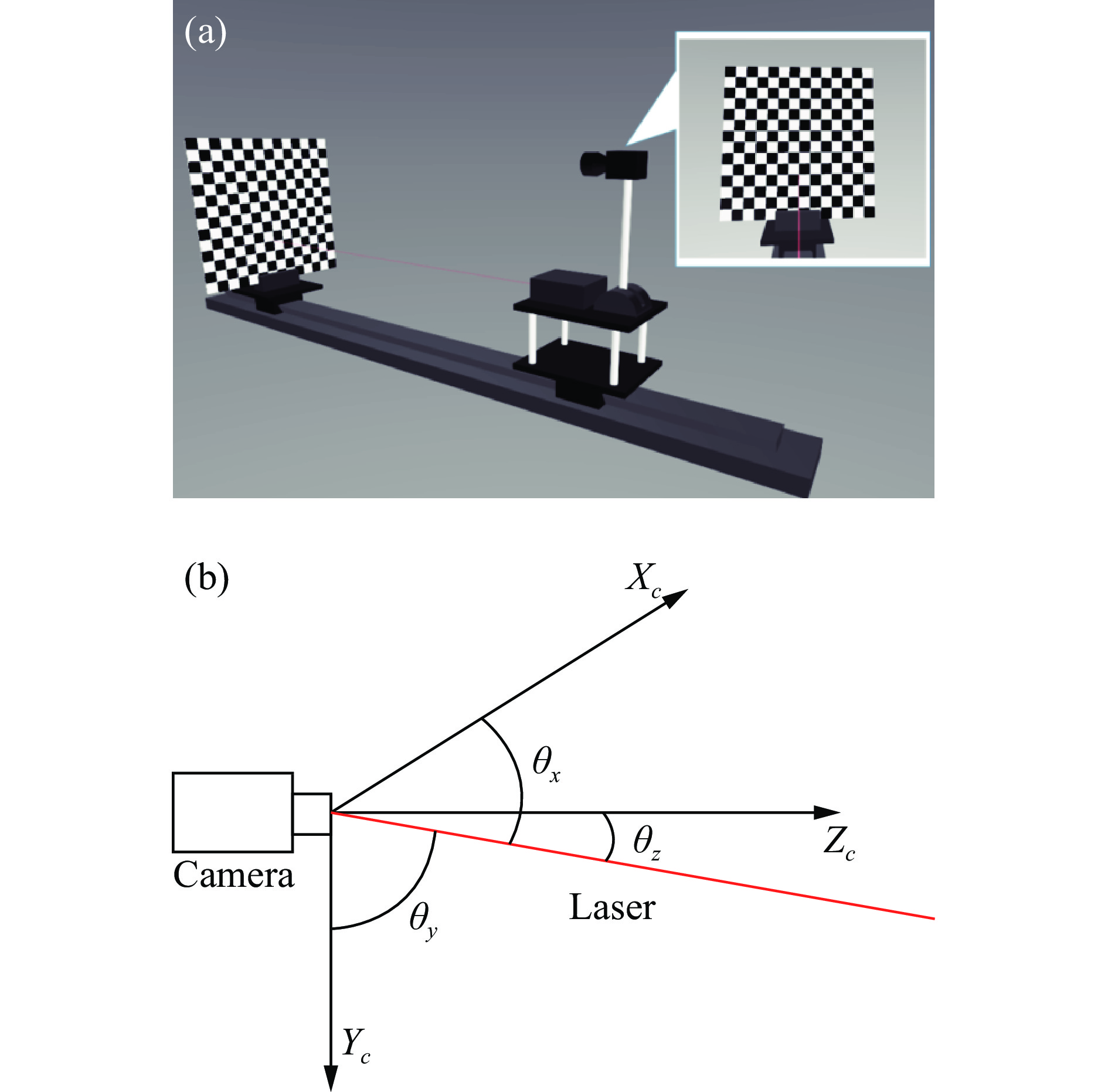
与二维或三维激光测距仪的标定相比,单点激光测距仪的标定是完全不同的。具体的标定图如图1(a)所示。在该示意图中,激光光斑位于棋盘上,并且其在相机坐标系中的3D坐标可以用6个变量表示。假设激光测距仪的返回距离值为L,然后光点的相机坐标可写为:

图 1 (a) 激光测距仪和相机标定示意图 ,(b) 激光与相机坐标轴之间的角度
Figure 1. (a) Laser range finder and camera calibration diagram, (b) Angle between laser and camera axes
$$ \left[ {\begin{array}{*{20}{c}} {{X_c}}\\ {{Y_c}}\\ {{Z_c}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {L\cos {\theta _x} + {t_x}}\\ {L\cos {\theta _y} + {t_y}}\\ {L\cos {\theta _z} + {t_z}} \end{array}} \right] $$ (1) 式中:
${X_c},{Y_c},{Z_c}$ 是相机坐标系中的坐标;L代表激光测距仪返回的距离值。如图1(b)所示,$\left( {{\theta _x},{\theta _y},{\theta _z}} \right)$ 是光线和相机坐标轴之间的角度,平移矢量$\left( {{t_x},{t_y},{t_z}} \right)$ 相机中心和激光测距仪之间的偏移。然而图1(b)中,光线与相机坐标轴之间的角度$\left( {{\theta _x},{\theta _y},{\theta _z}} \right)$ 满足以下方程:$${\rm co{s}^2}{\theta _x} + {\rm co{s}^2}{\theta _y} + {\rm co{s}^2}{\theta _z} = 1$$ (2) 这样,相机坐标系中的光点只需要5个变量:
$$\left[ {\begin{array}{*{20}{c}} {L{\rm cos}{\theta _x} + {t_x}}\\ {L{\rm cos}{\theta _y} + {t_y}}\\ {L\sqrt {1 - {\rm co{s}^2}{\theta _x} - {\rm co{s}^2}{\theta _y}} + {t_z}} \end{array}} \right]$$ (3) 而对于外参标定就是要求解这5个变量,传统的二维或三维激光测距仪标定,因为能够提供激光光斑的距离和角度,而且有若干个光斑点,可以建立的约束方程个数也多,而对于单点激光测距仪只有距离值可以应用,因此像之前的二维或者三维激光测距仪那样建立校正参数矩阵是很困难的。文中从光斑点的约束条件出发提出了两种标定单点激光测距仪和相机的方法。
-
第一种方法是在相机图像中有效地使用激光测距仪光斑点的成像,并利用激光光斑的像素坐标来建立约束方程。对于具体方法,可以参考图2。L1和L2表示当光斑落在不同平面上时激光测距仪的不同测量值。π1和π2代表不同的棋盘平面。
$\left( {u1,v1} \right)$ 和(u2,v2)是图像平面上不同平面上的斑点的像素坐标。由于文中使用的是光学波长在可见光范围内的激光测距仪,肉眼可以观察到相机中存在激光光斑。按照一般的模型,相机可以用针孔模型来描述。从相机坐标
$P = {\left( {X,Y,Z} \right)^{\rm{T}}}$ 到图像坐标$p = {\left( {u,v} \right)^{\rm{T}}}$ 的投影可以表示为[9]:$$p\sim KP$$ (4) 式中:K是相机内参矩阵;“~”表示点p的实际坐标与右手方程相差一个比例因子。在文中,假设矩阵K已经预先标定,并且激光光斑的图像坐标为
${\left( {u,v} \right)^{\rm{T}}}$ ,根据相机成像模型,结合激光光斑的相机坐标,可以得到如下方程:$$\frac{{{f_x}\left( {Lcos{\theta _x} + {t_x}} \right)}}{{L\sqrt {1 - co{s^2}{\theta _x} - co{s^2}{\theta _y}} + {t_z}}} + {u_0} = u$$ (5) $$\frac{{{f_y}\left( {Lcos{\theta _y} + {t_y}} \right)}}{{L\sqrt {1 - co{s^2}{\theta _x} - co{s^2}{\theta _y}} + {t_z}}} + {v_0} = v$$ (6) 式中:
$\left( {{f_x},{f_y}} \right)$ 是图像轴上的有效焦距;${\left( {{u_0},{v_0}} \right)^{\rm{T}}}$ 是投影的中心;L是激光测距仪返回的距离。给定3个或更多图像,通过观察标定棋盘上的激光光斑,联立方程(5)和(6),并用最小二乘法求解未知向量$\left( {{\theta _x},{\theta _y},{t_x},{t_y},{t_z}} \right)$ 。 -
实际的工业应用中,激光测距仪的光斑不是总是可见的,因此第一种标定方法有其限制范围,并且一些应用要求激光测距仪测量相机视场外的点,因此需要建立光斑不可见情况下的外参标定约束方程。图3为光斑不可见的标定模型。L1和L2表示当光斑落在不同平面上时激光测距仪的不同测量值。π1和π2代表不同的棋盘平面。
$\left( {R1,T1} \right)$ 和$\left( {R2,T2} \right)$ 表示不同棋盘平面上世界坐标系与的相机坐标系之间的位置关系。在图3的标定方法中,激光光斑是不可见的并且仅能知道观测距离信息。受Zhang和Pless[9]工作的启发,文中使用棋盘作为参考平面,并将激光光斑落在已知相对于相机位置的参考平面。根据Zhang的方法,可以在相机标定后得到棋盘平面的法向量,从而得到相机坐标系中的平面方程。因此当激光光斑落在棋盘上时,激光光斑的相机坐标应满足相机坐标系中棋盘平面的方程。
同样地,相机通过针孔模型来描述,从世界坐标P=
$ {\left( {X,Y,Z} \right)^{\rm{T}}}$ 投影到图像坐标$p = {\left( {u,v} \right)^{\rm{T}}}$ 可以表示为[9-11]:$$p\sim K\left( {RP + t} \right)$$ (7) 式中:K是相机内参矩阵;R是表示相机方向的3×3正交矩阵;t是表示其位置的3×1向量。
方法2是在笔者的系统前面放置一个平面图形,例如棋盘格,它对相机和激光测距仪都是可见的,如图3所示。为了简单起见,下面所说的标定平面,指的就是棋盘定义的平面。
在不失一般性的情况下,假设标定平面是世界坐标系中的平面Z=0。在相机坐标系中,标定平面可由3个矢量N参数化,使N与标定平面的法向量平行。通过相机的成像模型,可以得出:
$$N = - {R_3}\left( {R_3^{\rm{T}} \cdot t} \right)$$ (8) 式中:R3是旋转矩阵R的第3列;t是世界坐标中相机的中心。已知棋盘格平面的法向量,就可以得到棋盘格的平面方程。
假设棋盘平面
$\pi = {\left( {a,b,c,d} \right)^{\rm{T}}}$ ,激光光斑落在棋盘上。那么公式(3)给出的激光光斑X的相机坐标应满足平面π方程。这样可以得到以下线性方程:$$ \begin{array}{l} \pi \cdot X = \\ \left( {a,\;b,\;c,\;d} \right) \cdot \left( {\begin{array}{*{20}{c}} {L{\rm cos}{\theta _x} + {t_x}}\\ {L{\rm cos}{\theta _y} + {t_y}}\\ {\begin{array}{*{20}{c}} {L\sqrt {1 -{\rm co{s}^2}{\theta _x} - {\rm co{s}^2}{\theta _y}} + {t_z}}\\ 1 \end{array}} \end{array}} \right) = 0 \end{array} $$ (9) 再定义一个向量
$$A = {\left( {{\rm cos}{\theta _x},{\rm cos}{\theta _y},\sqrt {1 -{\rm co{s}^2}{\theta _x} - {\rm co{s}^2}{\theta _y}} } \right)^{\rm{T}}}$$ (10) 和一个向量
$$B = {\left( {{t_x},{t_y},{t_z}} \right)^{\rm{T}}}$$ (11) 然后上面的方程可以调整获得一个线性约束:
$$ \left( {\left( {a,\;b,\;c} \right)L \cdot \left( {a,\;b,\;c} \right)} \right)\left( {\begin{aligned} B\\ A \end{aligned}} \right) = - d $$ (12) 上述方程有5个未知变量,要使用至少5个输入图像,得到5组约束进行标定参量的求解。
方程解的存在性:方程要得到一个数值解,约束矩阵必须满秩。因此对于前3列,满秩意味着实验的所有平面的法向量张成一个秩为 3 的空间,也就表明实验中的平面不可能都是平行的,或者在空间中与一个方向平行。此外,后 3 列是相同的法向量的集合,只不过是按照不同的比例进行缩放的。同样地,为了保证满秩,对于单独一个姿态的棋盘格平面,其距离值应该不一样。综上所述,如果移动棋盘格平面到不同的距离,并且沿着空间三维不同的方向,那么这样的约束矩阵是满秩的。
-
在Zhang和Pless[9]的文章中证明了,对相机内参、平面位姿和激光测距机的相对位姿进行全局优化可以提高整体的标定精度。按照同样的方法,分别建立对于上面两种标定方法的优化方法。
按照Zhang的观点,相机的内参也要参与整体的优化,对此一个单一的优化方程:
$$F = \mathop \sum \nolimits_{i,j} \left( {\begin{array}{*{20}{c}} {{u_j}}\\ {{v_j}} \end{array}} \right) - proj{\left( {po{s_i} \cdot {W_j}} \right)^2}$$ (13) 可以用来表征对相机内参的优化。其中
${W_j} = {\left( {{X_j},{Y_j},{Z_j}} \right)^{\rm{T}}}$ 是已知三维点的坐标,${\left( {{u_j},{v_j}} \right)^{\rm{T}}}$ 是三维点的二维像素坐标,proj(·)函数是将相机坐标中的三维点映射到图像平面,i是实验次数,即棋盘平面上不同位置的个数,j是在实验中选择的不同点的个数。至于proj(·)函数,可以用相机的成像方程[12]来描述。对于一个完整的全局优化的目标函数可以表示为两项,一项是上面讨论的相机内参和平面姿态的目标函数,一项是优化激光测距机相对位姿的,所以一个完整的全局优化目标函数可以表述为:
$${{E}} = \mathop \sum \nolimits_{i,j} \left( {\begin{array}{*{20}{c}} {{u_j}}\\ {{v_j}} \end{array}} \right) - proj{\left( {po{s_i} \cdot {W_j}} \right)^2} + Q$$ (14) 对于两种不同的方法,函数Q是不同的。对于方法1,由于该方法直接使用激光光斑的可见性来建立模型,方法1的主要误差是像素偏差,因此函数Q可以写成如下:
$$ Q = \mathop \sum \nolimits_{i,j} \left( {\begin{array}{*{20}{c}} {{u_{0j}}}\\ {{v_{0j}}} \end{array}} \right) - cal{\left( {{L_i};\left( {{\theta _x},{\theta _y},{t_x},{t_y},{t_z}} \right)} \right)^2}$$ (15) 式中:
${\left( {{u_{0j}},{v_{0j}}} \right)^{\rm{T}}}$ 为激光光斑的二维像素坐标;cal(·)函数是利用标定结果计算激光光斑的像素坐标。但是,对于方法2,函数Q也不能被忽略,其定义如下:
$$ Q = \mathop \sum \nolimits_i \left( {{\text{π} _i}{L_i} \cdot {\pi _i}} \right)\left( {\begin{array}{*{20}{c}} B\\ A \end{array}} \right) + {d_i}^2 $$ (16) 在这种情况下,文中通过将函数E最小化来优化提出的标定方法。
-
基于以上描述,文中分别按照上述的两种方法进行实验。实验硬件平台包括计算机和通过互联网接入连接到计算机的单目相机。计算机的操作系统是Windows XP。两个激光测距仪,其中一个激光光斑可见,另一个不可见。具有不可见光斑的激光测距仪的波长为905 nm,可见光斑的激光测距仪为普通红波段,使用的相机为MV-EM系列的工业相机,最高分辨率为1 280×960。
对于方法1,具体操作为使用相机直接观察棋盘,并检测激光光斑。详细的原理图如图2所示。为了追求高精度,在随机位置捕获30个平面姿态,并检测每个图像中激光光斑的像素坐标。通过求解公式(5)和(6)得到未知变量
$\left( {{\theta _x},{\theta _y},{t_x},{t_y},{t_z}} \right)$ 。变量${\theta _x}$ 和${\theta _y}$ 表征激光的方向,$\left( {{t_x},{t_y},{t_z}} \right)$ 表示激光位置。在实际实验中,只有位置变量$\left( {{t_x},{t_y},{t_z}} \right)$ 可以通过实际测量轻松获得,因此文中后续将实际位置与作为方程解的变量进行比较,并将比较结果作为评估方法。如图2所示,在不同位置拍摄6张棋盘图片,图片如图4所示,并且通过最小二乘法求解公式(5)和(6)得到校准参数。
可以看到,方法1的主要误差源是光斑像素坐标的测量误差和相机的内部参数误差,其中像素坐标的测量误差是主要误差源,因为相机的内部参数误差可以通过多次标定来校正。
对于方法1的主要误差源,在检测点的像素坐标时,通常通过选择多个点并计算重心来计算点的像素坐标,以尽量减小像素坐标对参数精度的影响。
对于方法2,由于激光光斑不可见,文中使用激光光斑位于棋盘平面上的约束条件来建立约束方程(12)。根据Zhang和Pless[12]的标定方法,可以得到每个位置的棋盘平面方程。在这种方法中,在随机位置捕获10个平面姿态,并利用张氏方法得到每个图像中的平面方程。通过求解方程(12),得到未知变量
$\left( {{\theta _x},{\theta _y},{t_x},{t_y},{t_z}} \right)$ 。由于存在误差,为了获得高精度,将优化等式(16)最小化以获得更准确的标定结果。具体的标定图像如图5所示。根据笔者拍摄的图片,计算了每个棋盘平面的具体参数
$\pi = {\left( {a,b,c,d} \right)^{\rm{T}}}$ 。具体数据如表1所示。得到每个棋盘平面的参数后,通过求解方程(12)得到未知变量$\left( {{\theta _x},{\theta _y},{t_x},{t_y},{t_z}} \right)$ 。表 1 棋盘平面的计算参数
Table 1. Calculation parameters of the chessboard plane
Image\parameter Parameter a Parameter b Parameter c Parameter d 1 79.481 9 −92.458 2 −3 716.7 −1.382 9e07 2 −117.033 3 137.264 9 −3 671.3 −1.351 1e07 3 413.226 3 −1 092 −3 180 −1.147 5e07 4 1 145.8 −686.871 5 −3 032.5 −1.09 8e07 5 99.424 9 −1 394 −2 943.6 −1.06 18e07 6 −1 331.8 292.370 5 −3 152.1 −1.179 5e07 类似地,很明显方法2的主要误差源是棋盘平面参数的求解,并且平面参数的求解涉及相机的内部参数,外部参数和其他因素,这些因素总是具有或多或少的误差。通过人工方法很难减少这种误差。只能收集尽可能多的图像来标定相机的内部和外部参数,以使相机的参数接近真实值。
在得到标定参数后,文中提出几种方法来评估标定结果。对于方法1和方法2,可以使用误差函数公式(15)来评估。通过比较参考图像中激光光斑的两个像素坐标,并根据标定参数计算,如图6所示。从图中可以清晰地看到,取自不同的棋盘姿态的同样数量的图片,方法1的表现明显优于方法2。
上图显示了收集相同数量图像的两种方法的比较结果,显然,方法1取得了良好的效果,因为图像数目相同的条件下,方法1的唯一影响因素是激光光斑的像素坐标。这与收集到的图像数量无关,更重要的是,当使用多个点计算重心时,像素坐标的影响已降至最小。方法2的影响因素包括相机外部参数,外部参数的精度与所收集的图像数量有关。收集的图像越多,外部参数就越准确。因此,在采集图像数量相同的条件下,方法1的表现明显优于方法2。而且文中最后的实际实验结果证实了笔者的推理。
另外,由于位置变量
$\left( {{t_x},{t_y},{t_z}} \right)$ 可以通过实际测量获得,文中定义了另一种评估方法:$$d = {\left\| {\left( {\begin{array}{*{20}{c}} {{t_{0x}}}\\ {{t_{0y}}}\\ {{t_{0z}}} \end{array}} \right) - \left( {\begin{array}{*{20}{c}} {{t_x}}\\ {{t_y}}\\ {{t_z}} \end{array}} \right)} \right\|^2}$$ (17) 式中:
$\left( {{t_{0x}},{t_{0y}},{t_{0z}}} \right)$ 为实际激光位置。通过绘制了方法1和方法2在不同棋盘姿态下实际激光位置与计算位置之间的误差d,来评价标定参数的精确性。这两种方法在超过15次测量中都有显著改善。具体比较结果如下:从图7可以看出,这两种方法对位移参数
$\left( {{t_x},{t_y},{t_z}} \right)$ 影响不大,两种方法都可以获得精确的位移参数。
图 6 激光光斑的实际位置和计算位置的比较。 (a)红色矩形是通过方法1计算的位置; (b)蓝色矩形是通过方法2计算的位置
Figure 6. Comparison of the actual position and calculated position of the laser spot. (a) Red rectangle is the position calculated by method 1; (b) Blue rectangle is the position calculated by method 2

图 7 方法1和方法2中不同数量的棋盘姿态的位置误差
Figure 7. Position error of different number of checkerboard postures in methods 1 and 2
更重要的是,文中特别比较了进行全局优化的方法与没有全局优化的标定结果。结果如图8所示,原始误差用绿色表示,包括相机内参误差在内的完全优化用红色表示,由此可以看出,全局优化后标定结果的误差明显较小,因为它综合考虑了影响标定过程中标定精度的各种因素,并进行了全面优化。

图 8 方法1(上)和方法2(下)的位置误差分布
Figure 8. Position error distribution for method 1 (top) and method 2 (bottom)
图8是优化和无优化的比较结果。优化后,将方法1或方法2的所有可能影响因素整合到表达式中以优化结果。优化的优点是利用更多图像来获得更准确的参数。显然,优化后的误差小于没有优化的误差。
对于目前存在的标定算法,将文中算法与其做了对比,对比结果如表2所示。
表 2 三种标定算法对比
Table 2. Comparison of three calibration algorithms
Existing algorithm Method 1 Method 2 $\left( {{\theta _x},{\theta _y}} \right)$ (1.556,1.588) (1.557,1.586) (1.561,1.590) $\left( {{t_x},{t_y},{t_z}} \right)$ (0.04,−0.08,0.03) (0.04,−0.07,0.04) (0.06,−0.10,0.05) Time/s 0.153 0.063 0.106 很明显可以看出,在实际的标定结果上,文中算法与现存算法的结果相差不多,但是时间上确是消耗较少,而且方法一比方法二所需时间更少。由于所选样本太少,导致方法二的结果与其他两种方法存在一点偏差。
最后,文中将实际光斑与根据标定参数计算出的像素位置进行了比较。这两种方法都比最小测量集有显著的改进。可以看到,通过14次或更多的测量,方法1达到了可接受的水平。相反,方法2需要18次或更多次才能达到可比的精度。
从图9中可以明显看出,只要有足够的数据图像,参数值就可以收敛到真值,但显然方法1所需的图像数量较少,方法1更容易接近实际值。
-
文中提出了在信息融合过程中的单点激光测距仪和相机标定的两种方法。两种方法的使用条件不同,方法1需要对图像中的激光光斑进行距离收集和二维观测,而方法2只需要激光光斑落在棋盘格平面上,与激光光斑的可见度无关。实验部分的结果数据表明,这两种方法都可以用来标定单点激光测距仪关于相机的相对姿态,最后的各种评价方法的数据也证实了文中提出的方法是可靠和正确的。实验过程中对于给定棋盘格相同姿态数目,方法1的表现明显优于方法2,因为方法1的误差来源主要是像素坐标的提取,但是方法2只使用激光测距的距离观测信息,误差来源平面向量的求取,这与相机内参等参数关系较大,影响因素也较多,因此难以减小。因此,接下来的工作将研究获得更高精度的、适用性更高的位姿标定方法。
在获取了激光测距仪与相机的外部参数之后,利用激光测距仪的返回距离值,可以为单目相机的深度提取提供参考,大大提高单目相机的深度提取能力,在有图像信息的基础上能够拥有更精确的深度信息,这将有利于扩展相机与激光测距仪组合在工业应用中的范围和前景。
Calibration method of laser range finder and camera in information fusion process
-
摘要: 激光测距仪与视觉图像的融合研究在最近的工业机器人等应用领域中受到越来越多的关注,其中对这两种仪器的位姿标定有利于对二者信息的有效融合。以单点激光测距仪和相机的位姿融合为主要研究内容,提出两种确定两者相对位置和方向的标定方法,在建立光斑相机坐标的基础上分别以可见光斑和不可见光斑为研究内容,分别通过光斑的坐标和平面约束对两种情况建立标定方程,并结合实验验证两种标定方法的有效性和可靠性,实验结果表明:在有限次测量次数的情况下标定结果能够使重投影误差达到3个像素以内,而且运算时间大大减小。Abstract: The fusion of laser range finder (LRF) and visual image has received more and more attention in recent applications such as industrial robots. The calibration of the poses of these two instruments was conducive to the effective fusion of the two information. The single-point laser range finder and the camera's pose fusion were the main research contents. Two calibration methods for determining the relative position and direction of the two were proposed. Based on the coordinates of the spot camera, the spot was visible and the spot was invisible as the research content. The research content establishes the calibration equations for the two cases by the coordinates of the spot and the plane constraint respectively, and the validity and reliability of the two calibration methods were verified by experiments. The experimental results show that the calibration results can be made in the case of a limited number of measurements. The re-projection error is within 3 pixels, and the computation time is greatly reduced.
-
Key words:
- single-point /
- laser range finder /
- calibration /
- high reliability
-
表 1 棋盘平面的计算参数
Table 1. Calculation parameters of the chessboard plane
Image\parameter Parameter a Parameter b Parameter c Parameter d 1 79.481 9 −92.458 2 −3 716.7 −1.382 9e07 2 −117.033 3 137.264 9 −3 671.3 −1.351 1e07 3 413.226 3 −1 092 −3 180 −1.147 5e07 4 1 145.8 −686.871 5 −3 032.5 −1.09 8e07 5 99.424 9 −1 394 −2 943.6 −1.06 18e07 6 −1 331.8 292.370 5 −3 152.1 −1.179 5e07 表 2 三种标定算法对比
Table 2. Comparison of three calibration algorithms
Existing algorithm Method 1 Method 2 $\left( {{\theta _x},{\theta _y}} \right)$ (1.556,1.588) (1.557,1.586) (1.561,1.590) $\left( {{t_x},{t_y},{t_z}} \right)$ (0.04,−0.08,0.03) (0.04,−0.07,0.04) (0.06,−0.10,0.05) Time/s 0.153 0.063 0.106 -
[1] Cui Wei, Xiang Qian. Design and study of high precision laser rangefinder [J]. Laser Journal, 2018(7): 46−49. (in Chinese) [2] Song Hong, Zhang Yunfei, Wu Chaopeng. Calibration method of underwater phase laser ranging [J]. Infrared and Laser Engineering, 2019,48(4): 0406008. (in Chinese) doi: 10.3788/IRLA202049.0203004 [3] Zhang Xinlu, Zhang Su, Huang jinjer. Theoretical and experimental investigation of polarization coexistence and switching in an optical bistability Tm, Ho:LLF laser [J]. Optics Express, 2018, 26(14): 18783. doi: 10.1364/OE.26.018783 [4] Shwetak N P, Jun Rekimoto, Gregory D A. iCam: Precise at-a-Distance interaction in the physical environment[C]//International Conference on Pervasive Computing, 2006. [5] Wither J, Coffin C, Ventura J, et al. Fast annotation and modeling with a single-point laser range finder[C]//7th IEEE and ACM International Symposium on Mixed and Augmented Reality, 2008. [6] Vasconcelos F, Barreto J P, Nunes U. A minimal solution for the extrinsic calibration of a camera and a laser-rangefinder [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(11): 2097−2107. doi: 10.1109/TPAMI.2012.18 [7] Wenbo Dong, Volkan Isler. A novel method for the extrinsic calibration of a 2D laser rangefinder and a camera [J]. IEEE Sensors Journal, 2018(99): 1. [8] Aishwarya A P, Sam Shue, James M C. A survey of methods for mobile robot localization and mapping in dynamic indoor environments[C]//2018 Conference on Signal Processing And Communication Engineering Systems (SPACES). IEEE, 2018. [9] Zhang Q, Pless R. Extrinsic calibration of a camera and laser range finder (improves camera calibration)[C]//IEEE/RSJ International Conference on Intelligent Robots & Systems, 2005. [10] Scaramuzza, Davide, Harati, et al. Extrinsic self calibration of a camera and a 3D laser range finder from natural scenes[C]//2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2007. [11] Zhang Yuhai. Research on multi-camera coordinate measurement technology[D]. Hefei: University of Science and Technology of China, 2017.(in Chinese) [12] Vasconcelos Francisco, Barreto João P, Nunes Urbano. A minimal solution for the extrinsic calibration of a camera and a laser-rangefinder [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(11): 97−107. -






 下载:
下载: