-
随着光电稳定平台性能要求的进一步提高,系统稳态精度要求已达到微弧级别,以经典PID为代表的被动抗扰技术已难以满足光电稳定平台逐渐提高的抗扰性能需求[1-2],急需一种新的更高性能的控制策略。基于干扰估计的主动抗扰技术成为一个新的研究热点[3-4],由中国科学院韩京清研究员提出的自抗扰控制算法为其中的典型代表,由于其原理简单、控制效果优异取得了丰富的成果[4-5],随着高志强教授等对自抗扰算法的线性化及基于带宽的参数配置研究,大大促进了其在工程上的应用,自抗扰控制在光电稳定平台上的应用也是一个重要的研究方向:参考文献[6-7]将线性自抗扰控制引入光电稳定平台控制,并仿真证明了其相对于现有经典控制算法,如PID、PI等抗干扰能力有明显增强;
然而自抗扰控制算法存在着以下几个缺点:(1)由于观测器阶数的提高不可避免的造成大延迟,参考文献[8]给出了降阶自抗扰控制的设计及参数整定方法,通过降阶虽然降低了系统的延迟,但其需要相关传感器数据可信度高、信号微分效果好,而微分器的设计加剧了系统的延迟;(2)浪费了已知的模型及控制器信息。当前工程实际中,对于被控对象的模型信息一般是部分可知的,自抗扰控制算法假设模型为积分串联型,虽降低了控制器及观测器的设计难度,但造成了被控对象信息的浪费,参考文献[9]使用模型辅助的降阶自抗扰控制,在控制器设计中加入了模型信息,降低了扰动观测的负荷,仿真验证了该方法可以提高系统的带宽及抗扰能力,但未能跳出积分串联型的束缚,同时,直接采用PD控制,又导致了原控制器的信息浪费;(3)虽然自抗扰控制算法的设计符合分离定律,但对于一个已有控制系统,观测器及控制器均需重新设计,即摒弃了原有控制器信息,又增加了设计工作量。
针对以上缺点,文中提出一种扰动分离自抗扰控制算法,充分利用已知相关模型信息,实现原控制器复用,减少设计工作量的同时,提高系统控制精度。以某型两轴四框光电稳定平台的内框稳定环为研究对象,首先,对光电稳定平台稳定环数学模型及稳态精度影响因素进行分析;然后,对扰动分离自抗扰控制算法设计过程进行阐述;之后,对扰动分离自抗扰算法的优越性进行了理论证明;最后,通过系统仿真及实物验证,证明了文中提出方法的有效性。
-
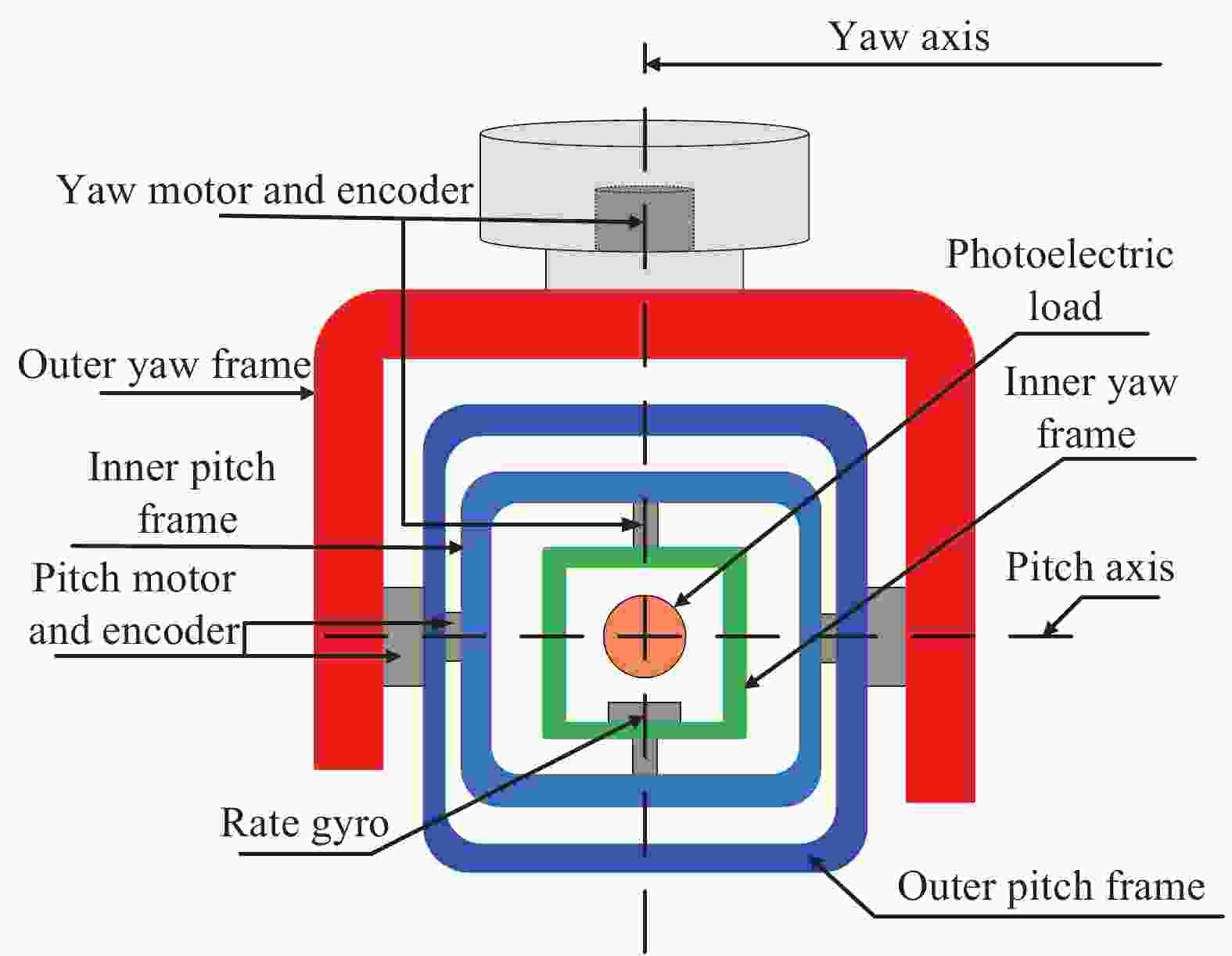
某型两轴四框架机载稳定平台框架结构如图1所示,系统的内框稳定环执行元件为某型力矩电机,被控对象为平台内方位或内俯仰框架及光电载荷,两轴光纤陀螺仪及两套光电码盘分别作为惯性速度及框架位置的反馈元件。
-
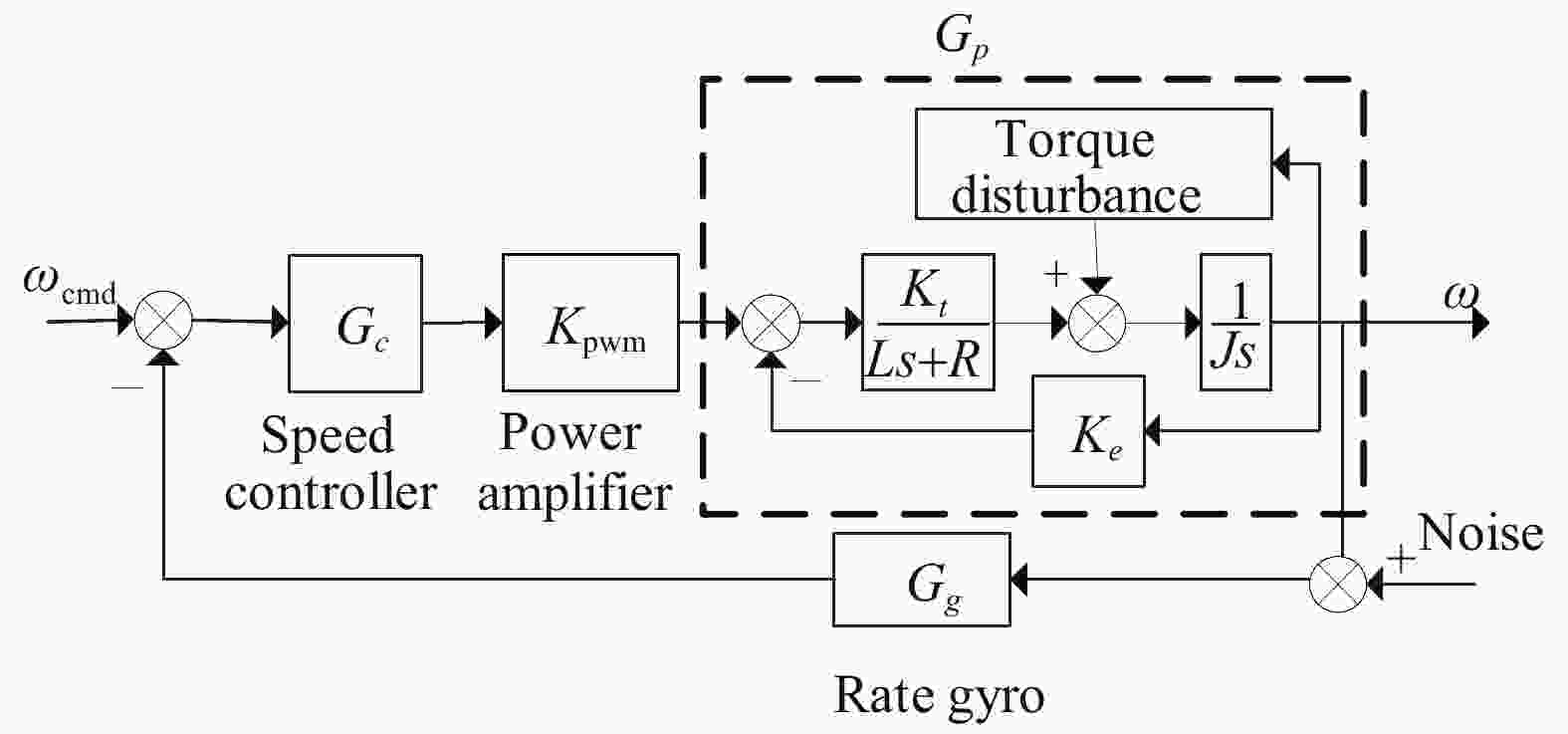
由于光电稳定平台各轴向的正交性,且控制方式基本类似[10-11],由直流电机原理,光电稳定平台某一轴向稳定环模型框图如图2所示。
图中,L、R分别为电机的电枢电感、电枢电阻,Kt为电机转矩系数,Ke
为反电动势系数,J为光电稳定平台框架转动惯量,ωcmd、ω分别为瞄准线角速度指令和输出值,在不考虑扰动的情况下,可建立被控对象Gp动态方程如公式(1)所示: $$ \left\{ \begin{aligned} & T = J\dot \omega \\& T = {K_t}i \\& u - {u_e} = L\frac{{{\rm d}i}}{{{\rm d}t}} + Ri \\& {u_e} = {K_e}\omega \end{aligned} \right. $$ (1) 消去中间变量得被控对象动态方程如下式所示:
$$ \ddot \omega = - \left(\frac{R}{L}\right)\dot \omega - \frac{{{K_t}{K_e}}}{{JL}}\omega + \frac{{{K_t}}}{{JL}}u $$ (2) R、L、Kt、Ke均可通过电机手册获得其理论值,由公式(2)通过拉氏变换可得系统理想的传递函数为:
$$ \phi (s) = \frac{\omega}{u} = \frac{1}{{{K_e}}}\frac{1}{{({T_m}s + 1)({T_{ e}}s + 1)}} $$ (3) 式中:
${T_m} = JR/{K_{ e}}{K_t}、{T_{ e}} = L/R$ ,分别为电机机电时间常数和电磁时间常数。 -
光电稳定平台所受到的扰动主要可分为两类:一类为影响系统动态的内部参数摄动及未建模动态;另一类为不影响系统稳定性的外部扰动。前者主要包括由环境引起的参数摄动及未建模的非线性部分或建模忽略的部分,后者主要包括系统的轴系摩擦、载机扰动、外界力矩扰动以及陀螺输出噪声等。易知,第一类扰动可等效为被控对象输入端的扰动量。对于被控对象而言第二类扰动的作用点如图3所示。
图中,Td表示系统的力矩扰动,包括了轴系摩擦及外部力矩干扰,ωb表示载机耦合到稳定环上的扰动,M1(s)=
$\dfrac{{{K_t}}}{{Ls + R}}$ 表示电机的力矩输出特性。陀螺测量噪声主要靠滤波器进行处理。由图3可知,在干扰力矩作用下系统的运动方程如公式(4)所示:$$ {T_m} = {M_1}(u - {u_e}) = {T_d} + Js{\omega} $$ (4) 同时易得:
$$ {u_e} = {K_e}({\omega} - {\omega_b}) $$ (5) 联合公式(4)和公式(5)可得:
$$ {\omega}(s) = \frac{{{M_1}}}{{Js + {K_e}{M_1}}}\left(u + {K_e}{\omega_b} - \frac{1}{{{M_1}}}{T_d}\right) $$ (6) 取:
$$ {u_d} = {K_e}{\omega_b} - \frac{1}{{{M_1}}}{T_d} $$ (7) 由公式(6)和公式(7)可知,无论是系统的力矩扰动,还是载机扰动均可等效到被控对象输入端的一个等效电压扰动
${u_d}$ 上,其中力矩扰动可通过系统前馈通道等效,而载机扰动可通过系统反馈通道等效。取
${x_1} = \omega$ 及${x_2} = \dot \omega$ 为状态变量,考虑等效扰动${u_d}$ ,光电稳定平台某一轴向被控对象的状态空间数学模型如公式(8)所示:$$ \left\{ \begin{aligned} & {{\dot x}_1} = {x_2} \\& {{\dot x}_2} = - \frac{{{K_t}{K_e}}}{{JL}}{x_{^1}} - \left(\frac{R}{L}\right){x_{^2}} + \frac{{{K_t}}}{{JL}}(u + {u_d}) \\& y = Cx \end{aligned} \right. $$ (8) 即只要通过某种方式将系统模型中的等效电压扰动
${u_d}$ 消除就可以实现被控对象中扰动的抑制。这符合自抗扰控制的“总扰动思想”,自抗扰控制将异于标准积分串联型的部分全部作为系统扰动,通过对该扰动的补偿,使系统模型等效为标准积分串联型,如此将导致问题:系统理论模型发生改变,原控制器失效,需重新设计系统控制器;浪费已知的模型信息,增加了观测器的负荷,降低了观测器的精度。而文中提出的扰动分离自抗扰算法可以解决上述问题。 -
文中提出的扰动分离自抗扰控制算法,能够通过将被控对象实际模型补偿为传统算法设计时所使用的理论模型,从而实现对传统控制器设计信息的复用。即:文中提出算法可实现在不改变原控制系统的基础上对控制系统算法进行升级。
在机载光电稳定平台速度环设计中,期望频率法(EF)是一种常用的控制系统校正方法,仿真条件下其稳态精度约为几十微弧,具有算法实现简单,性能稳定的优点,但其对控制系统提升有限,已逐渐无法适应当前复杂的扰动环境。DSADRC能够在保留原控制器优点的同时提高系统扰动隔离度及系统稳态精度,将期望频率特性法设计的控制器作为原系统及扰动分离自抗扰系统的控制器。
-
以典型二阶开环特性作为系统的期望开环特性设计控制器,期望开环特性如公式(9)所示:
$$ {\phi _{\rm expect}} = 2{\text{π}} {\text{π}} {f_c}{f_c}\dfrac{{\left(\dfrac{1}{{{\text{π}} {f_c}}}s + 1\right)}}{{{s^2}\left(\dfrac{1}{{6{\text{π}} {f_c}}}s + 1\right)}} $$ (9) 式中:
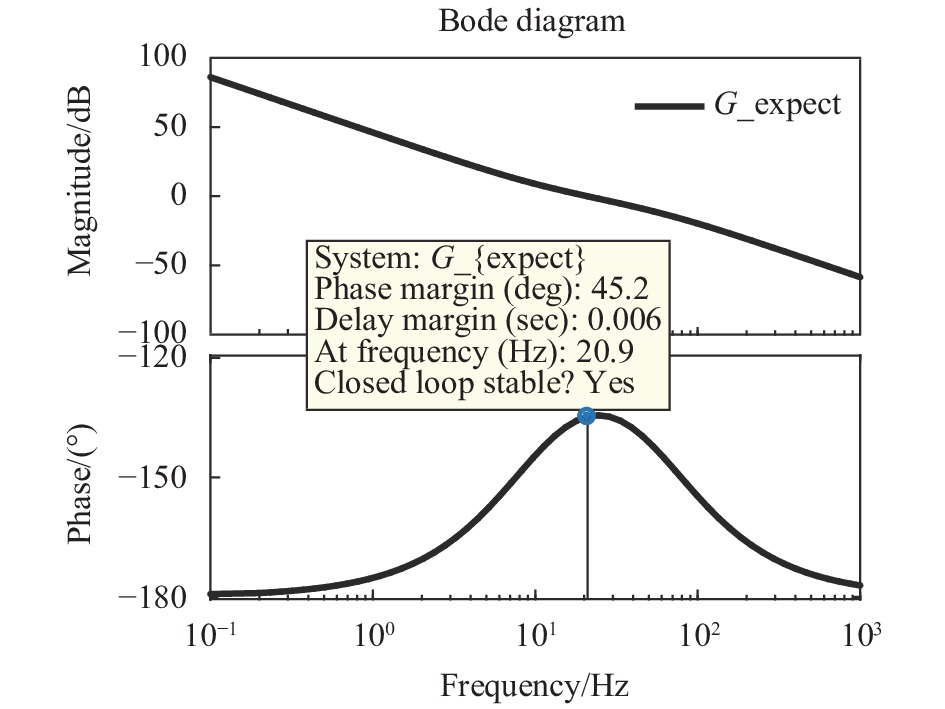
${f_c}$ 为期望截止频率,Hz。根据光电稳定平台指标要求,设计期望特性带宽为20 Hz,其幅相特性曲线如图4所示。由公式(3)和公式(9)可得系统控制器如公式(10)所示:
$$ \begin{split} & {G_c} = \dfrac{{{\phi _{\rm expect}}}}{\phi } = \\&2{{\text{π}} ^2}{f_c}^2{K_e}\dfrac{{\left( {\dfrac{1}{{{\text{π}} {f_c}}}s + 1} \right)\left( {{T_m}s + 1} \right)\left( {{T_e}s + 1} \right)}}{{{s^2}\left(\dfrac{1}{{6{\text{π}} {f_c}}}s + 1\right)}} \end{split} $$ (10) 公式(10)上下多项式阶数相同,易知期望频域法本质上仍为超前滞后矫正,也即PID控制,只是通过期望频率来设计相关的控制器系数。
-
由公式(10)系统控制器可分为三个部分:
(1)增益控制部分
$$ {G_{c1}} = 2{{\text{π}} ^2}{f_c}^2{T_m}{T_e}{K_e} $$ (11) (2)超前矫正网络
$$ {G_{c2}} = \frac{{\dfrac{1}{{{\text{π}} {f_c}}}s + 1}}{{\dfrac{1}{{6{\text{π}} {f_c}}}s + 1}} $$ (12) (3)两个滞后校正网络(PI控制器)
$$ {G_{c3}} = 1 + \frac{1}{{{T_m}s}} $$ (13) $$ {G_{c4}} = 1 + \frac{1}{{{T_e}s}} $$ (14) 即使用期望频率特性设计的超前滞后控制器有一个超前网络,两个滞后网络,由于均为经典的校正网络,所以在工程实际中,无论使用硬件电路还是数字控制器均十分容易实现。
-
经典线性自抗扰控制下,原系统控制器无法复用的原因在于:经典自抗扰控制算法将积分串联型作为标准模型,而将异于该标准模型的其他部分均作为扰动并进行观测和补偿,即补偿后系统模型发生了变化,原控制器不在适用。而MLADRC虽加入了模型的信息,减少了观测负担,但其依然将系统作为标准的积分串联型进行补偿。
文中提出的扰动分离自抗扰算法,将已知的被控对象理论模型从总扰动中分离出来,以减少ESO的观测负担,提高观测精度,同时跳出标准的积分串联型,将系统按系统实际理论模型进行补偿,从而复用原控制器,减少系统设计复杂度。
为将系统扰动项分离出来,并充分利用已知系统理论模型,将系统异于理论模型的部分作为扰动等效至被控对象输入处,仅将等效扰动项作为系统扩张状态,即:
$$ {x_3} = f = \frac{{{K_t}}}{{JL}}{u_d} $$ (15) 则被控对象状态空间模型可重写为公式(16):
$$ \left\{ \begin{aligned} & {{\dot x}_1} = {x_2} \\& {{\dot x}_2} = - \frac{{{K_t}{K_e}}}{{JL}}{x_1} - \frac{R}{L}{x_2} + {x_3} + \frac{{{K_t}}}{{JL}}u \\& {{\dot x}_3} = h \end{aligned} \right. $$ (16) 其中
$$ h = \dot f $$ (17) 对上述系统设计基于扰动分离的扩张状态观测器如公式(18)所示:
$$ \left\{ \begin{aligned} & {{\dot {\textit{z}}}_1} = {{\textit{z}}_2} + {g_1}e \\& {{\dot {\textit{z}}}_2} = - \frac{{{K_t}{K_e}}}{{JL}}{{\textit{z}}_{1}} - \frac{R}{L}{{\textit{z}}_{^2}} + {{\textit{z}}_3} + \frac{{{K_t}}}{{JL}}u + {g_2}e \\& {{\dot {\textit{z}}}_3} = {g_3}e \\& e = y - {{\textit{z}}_1} \end{aligned}\right. $$ (18) 式中:
${{\textit{z}}_1},{{\textit{z}}_2},{{\textit{z}}_3}$ 为原系统状态变量${x_1},{x_2},{x_3}$ 的估计值;${g_1},{g_2},{g_3}$ 为待设计的误差反馈增益。则系统观测误差为:$$ \left\{ \begin{aligned} & {{\dot e}_1} = {e_2} - {g_1}{e_1} \\& {{\dot e}_2} = - \frac{{{K_t}{K_e}}}{{JL}}{e_1} - \frac{R}{L}{e_2} + {e_3} - {g_2}{e_1} \\& {{\dot e}_3} = h - {g_3}{e_1} \end{aligned} \right. $$ (19) 由公式(19)可得误差系统的特征多项式为:
$$ \lambda (s) = {s^3} + ({g_1} + {a_1}){s^2} + ({g_1}{a_1} + {g_2} + {a_0})s + {g_3} $$ (20) 根据观测器带宽配置法,将观测器特征方程根配置到
$- {\omega_{\rm o}}$ 处,令:$$ \lambda (s) = {(s + {\omega_{\rm o}})^3} $$ (21) 可知,只需取误差增益系数如公式(22)所示,即可使扩张状态观测器特征多项式满足Hurwitz条件,则可保证扩张状态观测器的收敛。
$$ \left\{ \begin{aligned} & {g_1} = 3{\omega_{\rm o}} - \frac{R}{L} \\& {g_2} = {\left(\frac{R}{L}\right)^2} - \frac{{3R}}{L}{\omega_{\rm o}} + 3{\omega_{\rm o}}^2 - \frac{{{K_t}{K_e}}}{{JL}} \\& {g_3} = {\omega_{\rm o}}^3 \\& {\omega_{\rm o}} > 0 \end{aligned} \right. $$ (22) 式中:
${\omega_{\rm o}}$ 为大于0的设计参数。选取适当的${\omega_{\rm o}}$ 则可保证:$$ \left\{ \begin{aligned} & \mathop {\lim }\limits_{t \to \infty } {{\textit{z}}_1}{\rm{ = }}{x_{\rm{1}}} \\& \mathop {\lim }\limits_{t \to \infty } {{\textit{z}}_2}{\rm{ = }}{x_2} \\& \mathop {\lim }\limits_{t \to \infty } {{\textit{z}}_3}{\rm{ = }}f \end{aligned} \right. $$ (23) 该设计的主要优点有:
(1)最小化待观测扰动量,将已知信息充分利用,并将已知扰动从扩张状态观测器中分离;
(2)可复用经典控制系统控制器,实现自抗扰控制方法与传统方法的结合,同时通过扰动补偿提高控制精度。
其整体结构如图5所示。
-
扰动分离的原理,即将异于系统理论模型的部分通过观测器及补偿器的设计消除掉,通过补偿的作用使对于控制器而言,补偿后的系统模型同理论模型一致。
在公式(23)的条件下,使用如下补偿器进行控制率设计:
$$ u = {u_c} - \frac{{{{\textit{z}}_3}}}{{{b_c}}} $$ (24) 式中:uc为控制器的输出;u为被控对象输入。取控制增益bc为:
$$ {b_c} = \frac{{{K_t}}}{{JL}} $$ (25) 将公式(23)、(24)代入公式(8)得:
$$ \left\{ \begin{aligned} & {{\dot x}_1} = {x_2} \\& {{\dot x}_2} = - \frac{{{K_t}{K_e}}}{{JL}}{x_{^1}} - \frac{R}{L}{x_{^2}} + \frac{{{K_t}}}{{JL}}{u_c} \\& y = Cx \end{aligned} \right. $$ (26) 由公式(26)可知,由扰动分离自抗扰补偿后的系统与原系统理论模型一致,故可以实现原系统控制器的复用,从而降低设计复杂度。
-
由第2节可知,自抗扰控制方式的稳态精度的决定因素为扩张状态观测器的估计精度,估计精度越高,则补偿效果越好,进而控制性能越好。该节通过证明基于扰动分离的扩张状态观测器的性能来说明基于扰动分离自抗扰的优越性。
-
由第2节的阐述,根据现代控制理论可得相对于输入
$y$ 三个估计状态的传递函数分别为:$$ \begin{split} & \frac{{{{\textit{z}}_{1\_y}}}}{y} = \frac{{(3\omega - {a_1}){s^2} + (3{\omega^2} - {a_0})s}}{{{{(s + \omega)}^3}}} + \frac{{{\omega^3}}}{{{{(s + \omega)}^3}}} \\ & \frac{{{{\textit{z}}_{2\_y}}}}{y} = \frac{{({a_1}^2 - 3{a_1}\omega + 3{\omega^2} - {a_0}){s^2}}}{{{{(s + \omega)}^3}}} + \\ &\qquad \frac{{({\omega^3} - 3{a_0}\omega + {a_0}{a_1})s}}{{{{(s + \omega)}^3}}} \\ & \frac{{{{\textit{z}}_{3\_y}}}}{y} = \frac{{{\omega^3}({s^2} + {a_1}s + {a_0})}}{{{{(s + \omega)}^3}}} \end{split} $$ (27) 同理可得:
$$ \begin{split} & \frac{{{{\textit{z}}_{1\_u}}}}{u} = \frac{{{b_0}s}}{{{{(s + \omega)}^3}}} \\& \frac{{{{\textit{z}}_{2\_u}}}}{u} = \frac{{{b_o}s(s + 3\omega - {a_1})}}{{{{(s + \omega)}^3}}} \\& \frac{{{{\textit{z}}_{3\_u}}}}{u} = - \frac{{{b_0}{\omega^3}}}{{{{(s + \omega)}^3}}} \end{split} $$ (28) 其中
$$ {a_1} = \frac{R}{L};\;\;{a_0} = \frac{{{K_t}{K_e}}}{{JL}} $$ (29) 分别为状态空间模型的理论参数,取基于扰动分离的扩张状态观测器估计误差为:
$$ {e_{ds}} = {{\textit{z}}_{3\_y}} + {{\textit{z}}_{3\_u}} - f $$ (30) -
将公式(27)、(28)代入公式(30),整理后可得:
$$ \begin{split} {e_{ds}} =& {F_3}\left[ {({a_1} - {A_1})s + ({a_0} - {A_0})} \right]y + \\ & {F_3}{\omega_{unknown}} + {F_3}\Delta bu \end{split} $$ (31) 式中:
${A_1}、{A_0}$ 分别表示系统模型的真实参数;$\Delta b$ 为系统实际控制增益与理论控制增益的差;${\omega_{unknown}}$ 为除参数不确定外的剩余未知扰动,其中比例系数$$ {F_3} = \frac{{{\omega^3}}}{{{{(s + \omega)}^3}}} $$ (32) 为转折频率约为
$\omega$ 的低通滤波器。为了进行对比同理可推导出传统线性扩张状态观测器的估计误差为:
$$ \begin{split} {e_{ladrc}} = &{F_3}( - {A_1}s - {A_0})y + \\ & {F_3}{f_{total}} + {F_3}\Delta b{u} \end{split} $$ (33) -
对比公式(31)与公式(33),易得到以下结论:
(1)扩张状态观测器的估计误差由三部分引起,其分别为:状态增益参数不确定性引起的误差;总扰动引起的误差;控制增益不确定性引起的误差,且每项前有相同的低通滤波器;
(2)对于状态增益引起的误差,在理论模型参数与系统实际参数差值小于一定范围:
$$ 0 < \left| {{a_i} - {A_i}} \right| < {A_i};{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 0,1 $$ (34) 该范围要求,设计扰动分离扩张状态观测器所用的理论参数,与系统实际参数误差小于100%,扰动分离的自抗扰的估计精度均高于传统扩张状态观测器,扰动观测精度提升率
${\eta _1}$ 为:$$ {\eta _1} = \left| {\frac{{\left| { - {A_1}s - {A_0}} \right| - \left| {\left[ {({a_1} - {A_1})s + ({a_0} - {A_0})} \right]} \right|}}{{\left| { - {A_1}s - {A_0}} \right|}}} \right| $$ (35) 式中:
$s = j\omega$ 。易知在公式(34)的条件下,扰动观测精度提升率$\eta $ 始终大于0,且在设计理论参数与实际参数相等${a_1} = {A_1},{a_0} = {A_0}$ 时,达到最大值100%。(3)对于总扰动引起的估计误差,由于扰动分离的作用,文中设计所使用的总扰动
$f$ 要小于传统自抗扰所定义的${f_{total}}$ ,故基于扰动分离扩张状态观测器估计精度第二项高于传统扩张状态观测器,即其提升比率取决于模型参数不确定性占总扰动的比例,其估计精度提升率为:$$ {\eta _2} = \frac{{{f_{total}} - f}}{{{f_{total}}}} $$ (1) (4)对于控制增益不确定性引起的误差,相同条件下,扰动估计残余误差相同。
-
根据第2节的阐述及扰动分离自抗扰控制原理,在Matlab/Simulink搭建扰动分离自抗扰控制算法仿真模型如图6所示,其中使用二阶环节表示陀螺,使用信号发生器仿真等效力矩扰动,被控对象中使用符号函数模拟系统摩擦扰动。对文中提出的算法进行阶跃响应及等效扰动抑制实验,并将实验结果与当前传统PID算法结果进行对比。
-
阶跃响应可以较好地反映系统的快速性、稳定性以及稳态误差,故设计阶跃响应仿真实验对文中所提算法进行验证。
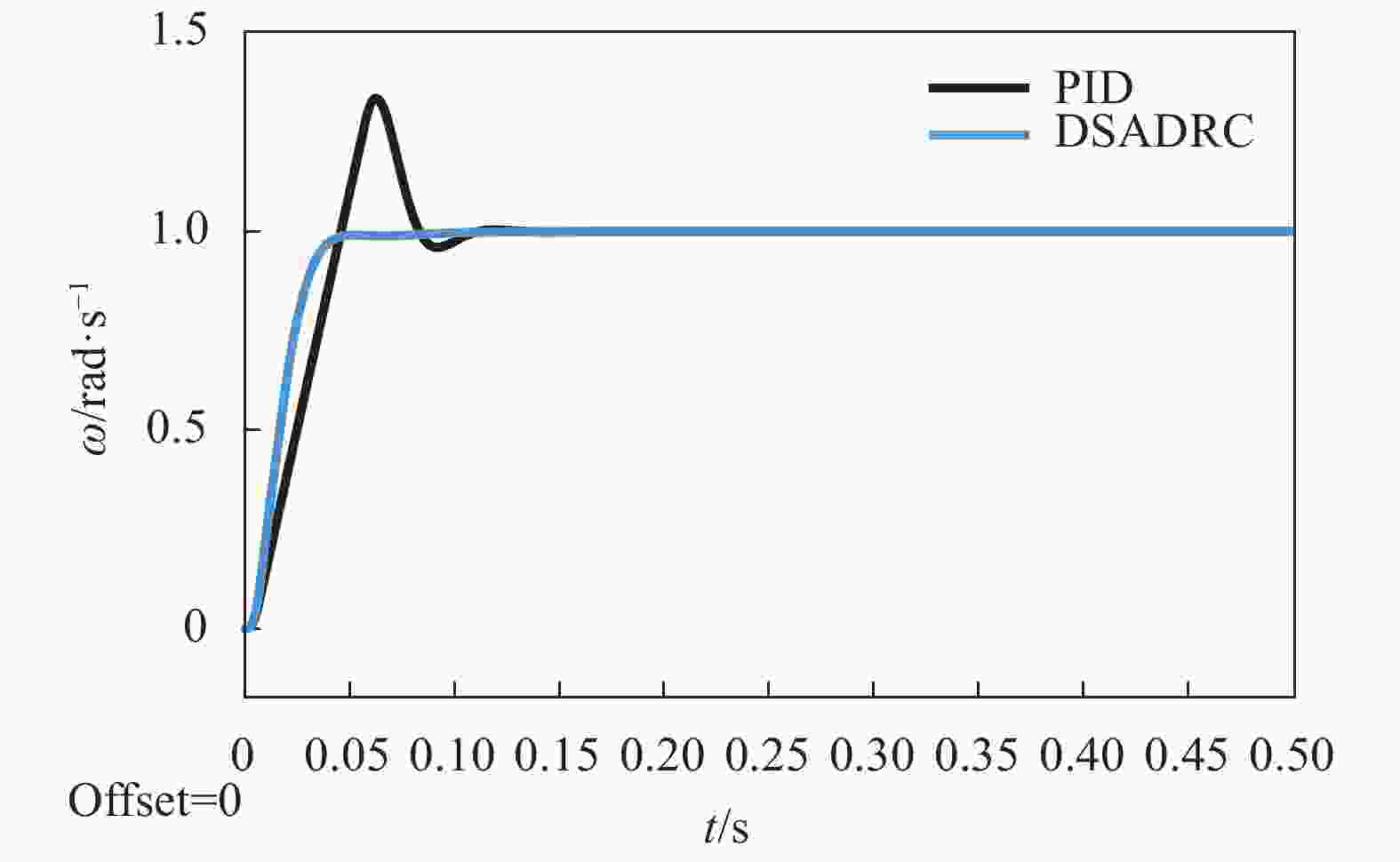
实验输入条件:系统控制器均为第2.1节设计的超前滞后网络,在不考虑等效扰动的情况下,给定幅值为1 rad/s的阶跃信号作为系统指令信号,为了解决超调量与快速性的矛盾,在阶跃指令信号后串联时间常数为0.02的惯性环节作为过渡过程安排,考察扰动分离自抗扰控制与传统控制方法的阶跃速度输出,通过调节时间(2%误差带)、上升时间(10%~90%)及超调量对算法性能进行考察。仿真实验结果如表1及图7所示。
表 1 阶跃响应指标对比
Table 1. Step response index comparison
Overshoot Rise time/s Settling time/s PID 35.2% 0.034 0.102 DSADRC 0% 0.025 0.042 由仿真结果可知,在相同扰动条件及相同,且控制器相同的条件下,使用了文中提出的扰动分离自抗扰控制算法的系统,在超调量、上升时间及调节时间上均优于传统的PID算法。
图中,相对于传统PID算法,DSADRC算法调节时间减少58.8%,上升时间减少26.5%,无超调量,在响应速度及动态性能上远优于传统PID算法。
-
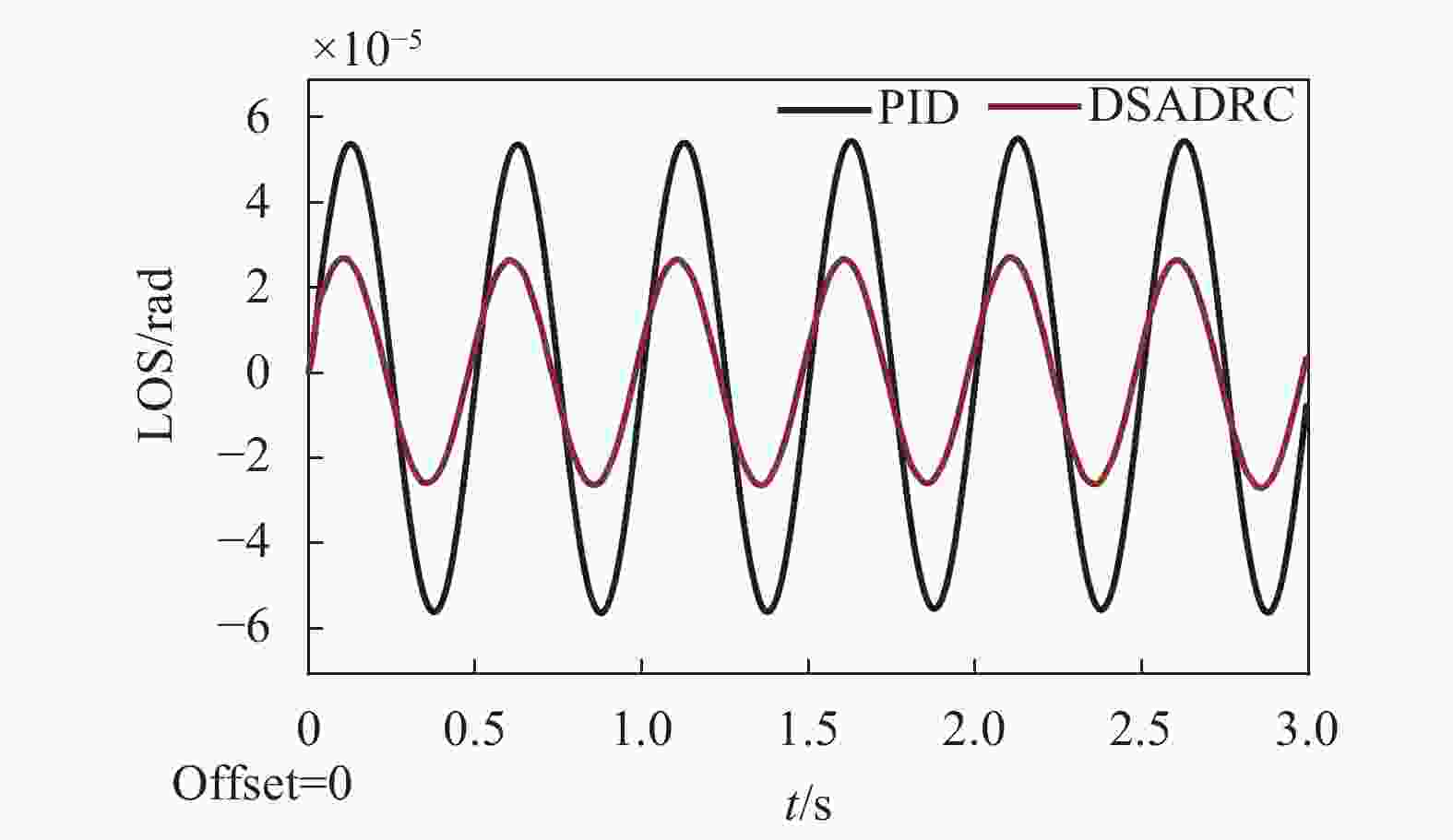
根据第1.2节的扰动分析,系统的扰动可等效至被控对象输入端,基于此,在图6的仿真模型Equivalent disturbance处添加1V2Hz的等效扰动,对比使用扰动分离方式及传统PID方式系统的瞄准线位置偏差,仿真结果如图8所示。
由图8可知,在相同控制器,相同扰动条件下,传统PID控制算法的瞄准线稳态精度约为38.91 μrad,而扰动分离自抗扰控制的系统,瞄准线稳态精度约为18.87 μrad,相对于PID算法,DSADRC在该条件下稳态精度提高了51.50%,极大地提高了光电稳定平台的稳态精度,从图中也可以看出,扰动分离自抗扰控制的系统延迟更小。
表2列出了在等效扰动幅值为1 V,不同频率的扰动下系统的稳态精度对比。
表 2 不同频率等效扰动下的稳定精度仿真结果
Table 2. Simulation results of stabilization accuracy under equivalent disturbances at different frequencies
Disturbance frequency/Hz LOS deviation of PID control system/μrad LOS deviation of DSADRC control system/μrad 0.5 36.71 16.49 1 38.69 17.66 3 38.87 20.33 5 39.10 24.86 从表2可以看出,对于5 Hz内不同频率的等效力扰动,在同等条件下,扰动分离自抗扰算法相对于传统PID算法瞄准线稳态精度均有明显提高。
-
为了证明所提算法的有效性,证明在相同扰动条件下所提算法的扰动抑制能力优于传统控制算法,采用某型光电稳定平台验证件对扰动分离自抗扰算法进行实物验证,设计控制系统扰动抑制实验,并与传统的PID控制器进行对比分析。实验设备包括:装载虚拟负载、陀螺、电机等的某型光电稳定平台验证件一套、系统控制板及驱动板一套、调试计算机一台。
-
实验条件:将系统内框架固定在减震工装中,使稳定平台工作在惯性态,在系统pwm输出端添加幅值为500(100%电压输出为5000),2 Hz的等效力矩干扰;控制器相关参数与仿真实验参数一致。
实验方法:分别在采用传统的超前滞后控制器和扰动分离自抗扰控制的条件下,对系统输出速度数据进行采集,通过速度数据分析在干扰条件下系统瞄准线的偏差。
实验结果如图9所示。
由图9可知,在相同的等效扰动下,传统PID瞄准线稳态精度约为54.831 μrad,而基于扰动隔离的自抗扰控制器面准线稳态精度约为18.839 μrad,扰动隔离度相比传统PID方式提高了65.64%,提升效果明显。
令等效扰动幅值不变,改变其扰动频率,重复以上扰动抑制实验,实验结果如表3所示。
表 3 不同频率等效扰动下的稳定精度实验结果
Table 3. Experimental results of stabilization accuracy under equivalent disturbances at different frequencies
Disturbance frequency/Hz LOS deviation of DSADRC control system/μrad LOS deviation of PID control system/μrad 0.5 9.360 56.741 1 13.293 56.222 1.5 22.071 54.102 2 18.839 54.831 2.5 27.180 57.470 5 19.307 54.534 -
实验结果表明,扰动分离自抗扰控制技术扰动抑制能力远高于传统PID控制器,在5 Hz内扰动抑制能力相比于传统PID控制器提高了50%以上,与仿真结果相当。故扰动分离自抗扰控制能够更好的隔离可等效到被控对象输入处的扰动。
同时对于DSADRC算法实物验证稳定精度结并没有仿真实验稳定精度稳定的现象,经分析主要是由于以下几点原因造成的:
(1)虽然扰动分离算法不需要非常精确地模型信息,但是模型信息的准确度也是影响扰动观测精度的一个重要因素,实物验证时的DSADRC算法所用模型信息的准确度远不如仿真实验。
(2)仿真实验使用符号函数表示系统摩擦力,其仅能表示出摩擦力的大小和方向,而无法表示出实物系统中摩擦力随运动速度的非线性变化。
(3)仿真实验中,除摩擦扰动使用符号函数表示外,其余部分均为线性模型,而实际被控对象中存在的大量的非线性模态。
-
文中分析了当前光电稳定平台的系统模型及扰动作用原理,并提出一种可复用传统控制器的新型自抗扰控制算法—扰动分离自抗扰控制。该算法通过将可得到的系统模型信息引入自抗扰的设计中,将已知信息从系统扰动中分离出来,降低扰动观测器的负荷,同时以系统理论模型为最终的补偿目标,实现原控制器的复用,提高系统的动态性能及抗扰能力。以某型光电稳定平台为对象,设计了仿真及实物验证实验,详细的阐述了实验过程并与传统的PID算法进行对比分析。
实验结果表明,文中提出的扰动分离自抗扰控制算法,在快速性上相比于传统PID算法调节时间减少58.8%,上升时间减少26.5%且无超调量,在扰动抑制能力上,相比于传统在PID算法提升50%以上。
综上所述,文中提出的扰动分离自抗扰控制,具有运算量小、设计简单的优点,同时能够有效提高光电稳定平台的响应能力和抗扰能力,具有一定的理论价值及工程应用价值。
Application of a disturbance separation active disturbance rejection control in photoelectric stabilized platform
-
摘要: 针对当前光电稳定平台伺服系统中扰动抑制能力不足的问题,提出一种扰动分离自抗扰控制(DSADRC)算法。扰动分离自抗扰控制充分利用工程实际中可获取到的部分已知的光电稳定平台模型信息及经典控制中的控制器信息,并将其加入到自抗扰控制的设计中。该算法通过减少光电稳定平台系统中的总扰动量,增加系统的扰动观测精度及扰动抑制能力。同时,通过算法设计实现了经典控制器的复用,减少了设计工作量。仿真实验结果表明:在控制器相同、扰动条件相同的情况下,扰动分离自抗扰控制阶跃响应调节时间减少58.8%,上升时间减少26.5%,且无超调量;在1V2Hz等效扰动下,系统稳态精度提高51.5%,系统性能提升效果明显。在实物验证实验中,对于不同频率的等效扰动,相比PID控制,扰动分离自抗扰控制稳态精度提升50%以上,有效地提高了光电稳定平台的稳态精度。Abstract: Aiming at the problem of insufficient disturbance suppression capability in the current photoelectric stabilized platform servo system, a disturbance separation active disturbance rejection control (DSADRC) algorithm was proposed. The active disturbance rejection control method based on disturbance separation took full use of part of the known photoelectric stabilized platform model information and controller information in classical control that could be obtained in engineering practice, and added it to the design of active disturbance rejection control. This algorithm increased the disturbance observation accuracy and disturbance suppression of the system ability by reducing the total disturbance in the photoelectric stabilized platform system. At the same time, through proposed algorithm design, the reuse of classic controllers was realized and the design workload was reduced. The simulation results show that under the same controller and the same disturbance conditions, the step response settling time of the DSADRC is reduced by 58.8%, the rise time is reduced by 26.5%, and there is no overshoot; under the 1V2Hz equivalent disturbance, the system steady accuracy is increased by 51.5%, and the system performance is improved obviously. In the physical verification experiment, for equivalent disturbances of different frequencies, compared with PID control, the steady accuracy of the DSADRC is improved by more than 50%, which effectively improves the steady accuracy of the photoelectric stabilized platform.
-
表 1 阶跃响应指标对比
Table 1. Step response index comparison
Overshoot Rise time/s Settling time/s PID 35.2% 0.034 0.102 DSADRC 0% 0.025 0.042 表 2 不同频率等效扰动下的稳定精度仿真结果
Table 2. Simulation results of stabilization accuracy under equivalent disturbances at different frequencies
Disturbance frequency/Hz LOS deviation of PID control system/μrad LOS deviation of DSADRC control system/μrad 0.5 36.71 16.49 1 38.69 17.66 3 38.87 20.33 5 39.10 24.86 表 3 不同频率等效扰动下的稳定精度实验结果
Table 3. Experimental results of stabilization accuracy under equivalent disturbances at different frequencies
Disturbance frequency/Hz LOS deviation of DSADRC control system/μrad LOS deviation of PID control system/μrad 0.5 9.360 56.741 1 13.293 56.222 1.5 22.071 54.102 2 18.839 54.831 2.5 27.180 57.470 5 19.307 54.534 -
[1] Qi C, Fan S X, Xie X, et al. Research on control method for improving low speed performance and stable precision of electro-optic servo system [J]. Acta Armamentarii, 2018, 39(10): 1873-1882. (in Chinese) doi: 10.3969/j.issn.1000-1093.2018.10.001 [2] Li X T, Zhang B, Shen H H. Improvement of isolation degree of aerial photoelectrical stabilized platform based on ADRC [J]. Optics and Precision Engineering, 2014, 22(8): 2223-2231. (in Chinese) doi: 10.3788/OPE.20142208.2223 [3] Wei Z Y, Xu W Q, Zhang G L, et al. Active disturbance rejection control of aerospace electromechanical servo system [J]. Control Theory & Applications, 2021, 38(1): 73-80. (in Chinese) doi: 10.7641/CTA.2020.00059 [4] Li Z P, Na S D, Chang Z F. Research on the return-to-center control of a vehicle′s electric power steering system based on active disturbance rejection control [J]. Journal of Harbin Engineering University, 2020, 41(7): 1066-1072. (in Chinese) [5] Wang W T, Guo J, Jiang Z H, et al. Study on photoelectric tracking system based on ADRC [J]. Infrared and Laser Engineering, 2017, 46(2): 0217003. (in Chinese) doi: 10.3788/IRLA201746.0217003 [6] Zheng C Y, Zhang H G. ADRC based on disturbance rejection of airborne electro-optical stabilized platform[C]//2016 First IEEE International Conference on Computer Communication and the Internet (ICCCI), IEEE, 2016: 169-172. [7] Wei W, Dai M, Li J Q, et al. ADRC control system for airborne opto-electronic platform [J]. Optics and Precision Engineering, 2015, 23(8): 2296-2305. (in Chinese) doi: 10.3788/OPE.20152308.2296 [8] Huang P, Yang X L, Xiu J H, et al. Reduced-order active disturbance rejection control of fast steering mirror driven by VCA [J]. Optics and Precision Engineering, 2020, 28(6): 1365-1374. (in Chinese) doi: 10.3788/OPE.20202806.1365 [9] Wang C Y, Zhao S Q, Shi H W, et al. Linear active disturbance rejection control of airborne photoelectric stabilized platform [J]. Infrared and Laser Engineering, 2019, 48(12): 1213002. (in Chinese) doi: 10.3788/IRLA201948.1213002 [10] Zhang Y, Yang T, Li C, et al. Fuzzy-PID control for the position loop of aerial inertially stabilized platform [J]. Aerospace Science & Technology, 2014, 36: 21-26. doi: 10.1016/j.ast.2014.03.010 [11] Zhou X, Jia Y, Zhao Q, et al. Dual-rate-loop control based on disturbance observer of angular acceleration for a three-axis aerial inertially stabilized platform [J]. Isa Transactions, 2016, 63: 288-298. doi: 10.1016/j.isatra.2016.02.021 -






 下载:
下载: