-
合成孔径雷达（Synthetic Aperture Radar，SAR）可实现二维高分辨率成像从而为关注区域的对地观测提供了重要手段。高分辨率SAR图像的情报侦察具有十分重要的军事价值，对SAR图像进行分析，并对其中潜在的感兴趣目标进行分类识别是目前的研究热点[1-2]。对于一幅大场景SAR图像，目标识别系统先通过检测和鉴别操作剔除背景噪声以及自然杂波等因素的干扰，从而获得感兴趣目标的图像切片；再根据事先获取的训练样本，对这些待识别的目标进行判定，具体采用特征提取和分类决策算法等。特征提取对SAR图像进行统计分析、信号处理、层次分解获取其中包含目标特性的部分。常用的特征包括投影特征（如主成分分析（Principal Component Analysis，PCA））[3-5]、变换域特征（如单演信号）[6]、几何形状特征（如目标轮廓）[7-9]、电磁特征（如散射中心）[10-11]等。根据提取的特征，分类决策阶段采用适当的分类器进行测试样本的类别判决。常用的分类器包括K近邻（K-nearest neighbor，K-NN）[3]，支持向量机（Support Vector Machine，SVM）[12]，稀疏表示分类（Sparse Representation-based Classification，SRC）[4, 6, 12-13]、卷积神经网络（Convolutional Neural Network，CNN）[14-16]等。
近年来，随着压缩感知理论的发展和成熟，基于其开发的稀疏表示分类器在模式识别领域得到广泛运用。Wright等首次将稀疏表示引入人脸识别并验证了其有效性[17]。具体到SAR目标识别，稀疏表示分类的应用十分广泛并对多类特征具有良好的适应性。通过PCA进行特征提取并采用稀疏表示进行分类[12]。参考文献[13]结合随机投影和稀疏表示分类器。参考文献[6]采用稀疏表示分类器对分解得到的多个单演信号成分进行分类。然而，现有的基于稀疏表示分类的识别方法多采用基于最小重构误差的决策准则，即将测试样本判决为能够最优重构它的训练类别。尽管这一准则应用广泛且具有较强的稳健性，但在SAR目标识别中这种单一准则的决策思路存在一定的风险，具体原因如下：（一）重构误差准则中考虑当前类别所有样本对于测试样本的整体重构误差，缺乏对于该类别中最相似的单个或局部样本的考察；（二）由于SAR目标识别中场景的复杂性，存在诸如噪声干扰、部分遮挡等一系列扩展操作条件（Extended Operating Condition，EOC），这种情况下单一准则的稳定性往往不够。为此，文中提出结合多种决策重则的稀疏表示分类方法并在SAR目标识别中进行应用。文中方法在求解得到的稀疏表示系数的基础上设计了三种决策准则，分别是最小重构误差准则、最大系数能量准则和局部最小重构误差准则。最小重构误差原则即传统稀疏表示分类中采用的方法。最大系数能量准则分别计算各个类别的表示系数的能量，认为测试样本属于具有最高能量的类别。局部最小重构误差准则是选取各个类别中若干较大的系数进行测试样本的重构，然而根据局部样本的最小重构误差进行类别判断。根据三种准则下计算得到的决策变量，文中采用线性加权的方法对它们进行融合，进而根据融合后的决策变量进行目标识别。通过结合不同决策准则的优势，文中方法有利于提高最终决策的稳健性，提高识别算法对于扩展操作条件的适应性。为对提出方法进行测试，基于MSTAR数据集设置若干实验条件对多类典型地面车辆目标进行分类。实验结果表明，所提方法可有效提高稀疏表示分类的综合性能，提高识别的有效性及稳健性。
-
在压缩感知相关理解基础上，稀疏表示利用字典表示的方式对新样本进行描述和分析，后续根据重构结果对样本特性进行分析。假定全局字典为
$D = $ $ [{D^1},{D^2}, \cdots ,{D^C}] \in {{{R}}^{d \times N}}$ ，其中${D^i} \in {R^{d \times {N_i}}}(i = 1,2, \cdots ,C)$ 代表第$i$ 类的${N_i}$ 个原子（即训练样本）。对于未知样本$y$ ，稀疏表示过程如下：$$ \begin{array}{l} \hat x = \mathop {\arg \min }\limits_x {\left\| x \right\|_0}\\ {\rm{s}}{\rm{.t}}{\rm{. }}\left\| {y{\rm{ - }}Dx} \right\|_2^2 \leqslant \varepsilon \end{array} $$ (1) 式中：
$x$ 为系数矢量，具有稀疏性（即，其中只有少量的非零元素）；$\varepsilon $ 表示最终的重构误差。公式（1）作为NP-hard问题，难以直接求解。为此，人们通过
${\ell _{\rm{1}}}$ 范数替换${\ell _0}$ 范数，将其转换为便于快速求解的凸优化问题[16]。此外，还可以采用效率更高的正交匹配追踪算法（Orthogonal Matching Pursuit，OMP）[13]等贪婪算法获得公式（1）中问题的近似解。求解得到系数矢量实际反映了被表征样本与各类别训练样本之间的相关性。因此，通过对求解结果的分析可获得当前测试样本与各类别之间的相关性，从而对其类别进行判断。 -
在获得最优估计结果
$\hat x$ 的基础上，可设计适当准则对测试样本的所述类别进行判定。传统的SRC多是基于重构误差进行分类。文中在此基础上，额外设计了两种新的决策准则。 -
根据
$\hat x$ ，分类别对测试样本进行重构，计算对应的误差，如公式（2）所示：$$ {r_{{G}}}(i) = \left\| {y{\rm{ - }}{D_i}{{\hat x}_i}} \right\|_2^2(i = 1,2, \cdots ,C) $$ (2) 式中：
${\hat x_i}$ 为全局稀系数矢量中对应第$i$ 类别的部分。然后，根据最小重构误差进行决策，如公式（3）所示：$$ {\rm{identity }}(y){\rm{ = }}\mathop {\arg \min }\limits_i ({r_{{G}}}(i)) $$ (3) 最小重构误差准则通过稀疏表示的逆向思路考察不同训练类别对于测试样本的表示能力，具有较强的可靠性，是现有文献中大量采用的思路。然而，该准则难以充分考察每个类别对于测试样本的描述能力。此外，若测试样本来自扩展操作条件，与训练样本差异较大时，单一依靠全局最小重构误差的容错率较低。为此，文中设计其他两类判决准则对其进行补充。
-
在稀疏表示的框架下，求解的非零系数一般分布在测试样本真实对应的类别。因此，正确类别的系数能量相对更高。文中按照公式（4）分别计算各个训练类别的系数能量：
$$E(i) = \left\| {{{\hat x}_i}} \right\|_{}^2(i = 1,2, \cdots ,C)$$ (4) 然后，根据最大系数能量的原则判定目标类别如公式（5）所示：
$${\rm{identity }}(y){\rm{ = }}\mathop {\arg \max }\limits_i (E(i))$$ (5) 在最大系数能量准则下，测试样本需要与某一训练类别中的部分样本保持较高的相关性才能获得较大的系数能量。若某一错误类别中包含与当前测试样本高度相关的极少数样本时，其系数总体能量也不会很高。这一点在最小重构误差准则中往往难以体现。
-
由于SAR图像具有较强的方位角敏感性，与测试样本高度相关的训练样本实际集中在全局字典的局部原子上（与测试样本具有相近方位角）。因此，在各类别上的重构应当考虑在局部字典上进行。在文中设计的局部最小重构误差原则中，分别在各个训练类别上选取
$M$ 个最大系数，然而利用它们对应的原子进行重构：$${r_{\rm{L}}}(i) = \left\| {y{\rm{ - }}D_i^M\hat x_i^M} \right\|_2^2(i = 1,2, \cdots ,C)$$ (6) 式中：
$\hat x_i^M$ 代表第$i$ 类上$M$ 个最大的系数；$D_i^M$ 则为对应的原子。一般而言，根据SAR图像的方位角敏感性，其相关性在真实方位角邻近的[−5°，5°]区间内可以得到有效保持。为此，文中设置$M{\rm{ = }}10$ 。根据各个类别的局部重构误差，按照公式（3）相同的思路进行目标类别的决策。 -
如前文所述，各个决策准则均可以根据求解的系数矢量进行独立决策。若各个准则的决策一致，则它们相互印证，因而决策的可靠性很高。然而，若三个准则的判决结果不一致，则需要对它们的结果进行科学融合，获得更为可靠的结果。文中基于线性加权方式对三个准则的决策变量进行融合，首先将重构误差和系数能量转换为统一的形式。
重构误差采用公式（7）进行转换：
$${p_{\rm{r}}} = 1 - \dfrac{{r(i)}}{{\displaystyle\sum\limits_{j = 1}^C {r(j)} }}$$ (7) 式中：
$r(i)$ 代表第$i$ 类的重构误差，可分别对应最小重构误差中的${r_{\rm{G}}}(i)$ 或局部最小重构误差中的${r_{\rm{L}}}(i)$ 。能量系数采用公式（8）进行转换：
$${p_{\rm{E}}}{\rm{ = }}\frac{{E(i)}}{{\displaystyle\sum\limits_{j = 1}^C {E(i)} }}$$ (8) 经过转换，重构误差和系数能量均转换为0~1之间的“概率”形式。重构误差越小、系数能量越大，则测试样本属于该类别的概率越大。采用公式（9）所示的线性加权策略对三者转换后的决策变量进行融合：
$$P = {w_1}{p_1} + {w_2}{p_3} + {w_3}{p_3}$$ (9) 式中：
${p_1}$ ，${p_2}$ ，${p_3}$ 分别对应三个准则经过转换后的决策变量；${w_1}$ ，${w_2}$ ，${w_3}$ 为对应权值，满足和为1的约束。一般地，在缺乏有效先验的情况下，可经验性设置${w_1}$ ，${w_2}$ ，${w_3}$ 均为1/3。根据公式（9）输出的融合决策值，可按照最大概率的原则进行最终决策。 -
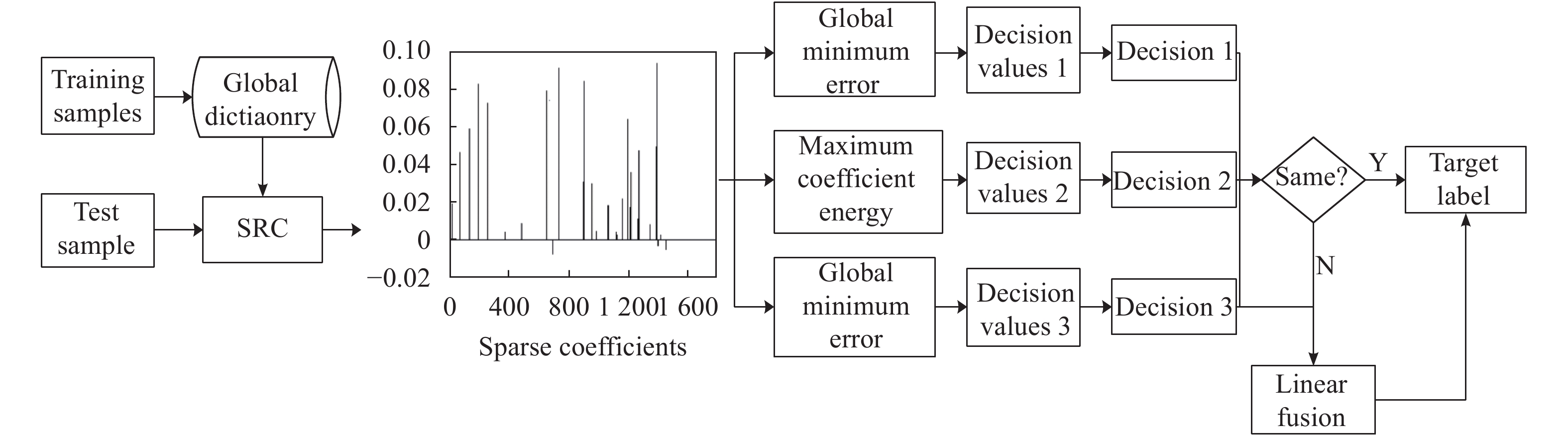
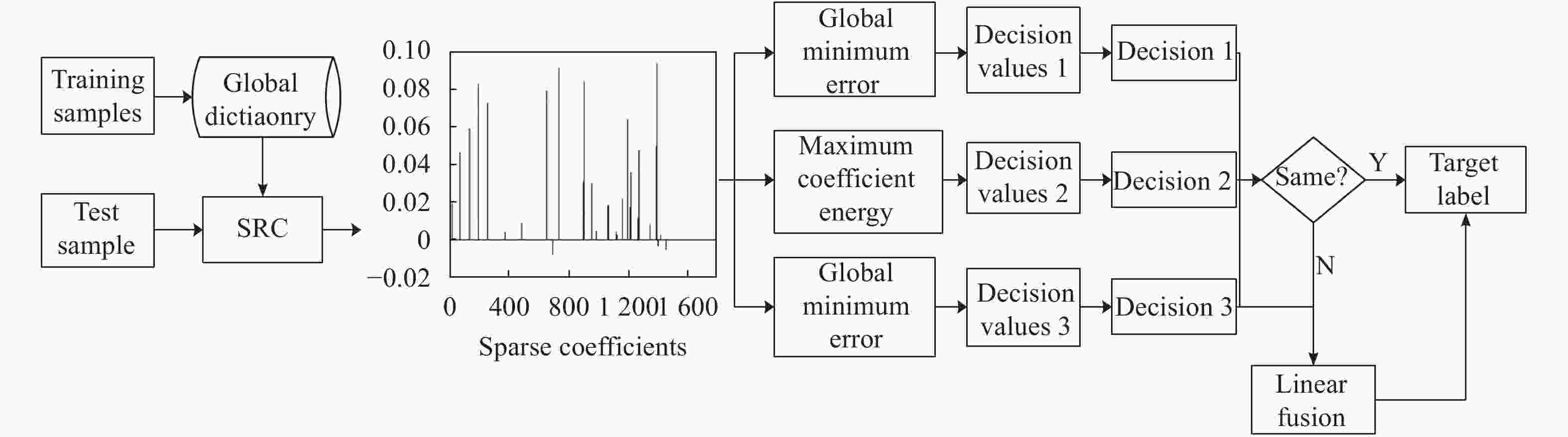
文中基于组合多决策准则的稀疏表示分类的SAR目标识别流程如图1所示。对于测试样本，首先在全局字典上对其进行稀疏表示。根据求解的系数矢量，分别在三个决策准则下计算决策变量并作出相应的决策。若三者的决策一直，则直接判定目标类别，识别流程结束。反之，若三者的决策结果不一致，则按照下文描述的具体算法那对三个决策变量进行融合，并根据融合结果判定目标类别。因此，文中通过在稀疏表示的框架下组合三种不同的决策准则有利于起到相互印证、相互补充的目的，从而提高最终决策精度。具体实施中，文中采用PCA对测试和训练样本进行特征提取；采用OMP算法求解稀疏系数。
图 1 所提方法的实施流程图
Figure 1. Flowchart of the proposed method
-
基于MSTAR数据集设置实验条件进行多类目标的分类实验。MSTAR数据作为当前广泛使用的SAR目标图像数据集，包含了多种条件下获取的10类车辆目标（光学及SAR图像示例见图2）。这些图像中，目标方位角覆盖0°~360°，部分目标存在若干子型号（如BMP2，T72）；原始图像分辨率达到0.3 m。表1给出了依托10类目标SAR图像设置的典型实验条件之一。其中，训练和测试集分别使用17°和15°俯仰角下的样本；BMP2和T72的测试集相对训练集包含更多子型号。当前设置条件下，训练和测试样本的差距相对较小，一般近似为标准操作条件（SOC）。
图 2 待识别目标图像
Figure 2. Imagery of targets to be recognized
表 1 基于MSTAR数据集的典型实验条件示例
Table 1. Typical experimental setup based on the MSTAR dataset
Class Training Test Configuration Number of images Configuration Number of images BMP2 9 563 233 9 563 195 9 566 196 c21 196 BTR70 c71 233 c71 196 T72 132 232 132 196 812 195 s7 191 T62 A51 299 A51 273 BRDM2 E-71 298 E-71 274 BTR60 7 532 256 7 532 195 ZSU23/4 d08 299 d08 274 D7 13 015 299 13 015 274 ZIL131 E12 299 E12 274 2S1 B01 299 B01 274 为验证组合多判决准则的有效性，将提出方法分别与不同准则下的SRC分类结果进行对比。为便于记录，后续将“最小重构误差准则”、“最大系数能量准则”以及“局部最小重构误差准则”下的SRC方法分别记为“SRC+准则1”（SRC+Principle 1）、“SRC+准则2”（SRC+Principle 2）和“SRC+准则3”（SRC+Principle 3）。此外，还选用性能优越的CNN方法进行同步对比[14]。
-
按照表1中的实验设置测试文中方法在标准操作条件下的分类性能。10类目标的识别结果展示如图3所示。其中，对角线元素反映了不同目标的正确识别率，均高于97.5%。采用4类对比方法在同样条件下进行分类实验，获得所有方法的平均识别率如表2所示。文中方法具有最高的平均识别率，表明其在标准操作条件下针对多类目标识别问题具有更强有效性。根据表1中的实验设置，BMP2和T72的测试样本与训练样本存在子型号差异，这一定程度增加了识别问题的难度，导致两者识别率相对较低。对于CNN方法，其分类性能十分依赖训练集的完备性，这导致训练的网络对于子型号差异的适应性较差。与其他单一决策准则下的SRC相比，文中通过多决策准则的联合显著提升了最终的识别性能。三种决策准则的分类结果可以相互印证和补充，通过决策变量的融合获得更为可靠的识别结果。因此，文中方法有利于提高当前标准操作条件下的识别性能。
图 3 标准操作条件下的混淆矩阵
Figure 3. Confusion matrix under SOC
表 2 标准操作条件下的结果对比
Table 2. Results comparison under SOC
Method type Average recognition rate Proposed 98.52% SRC+Principle 1 96.54% SRC+Principle 2 95.88% SRC+Principle 3 97.06% CNN 98.14% -
在标准操作条件的实验设置中，测试样本和训练样本的俯仰角接近（仅2°差异）。实际中，测试样本很可能与训练集来自较大差距的不同俯仰角。此时，由于俯仰角差异带来的图像差异增加了识别难度。表3给出了存在较大俯仰角差异的实验条件，采用17°俯仰角目标图像分别对30°和45°下的测试集进行分类。图4综合显示了各方法在两个俯仰角下的平均识别率。可以明显看出，在俯仰角45°时，各方法性能都出现显著下降。在两个测试条件下对比分析，文中方法均获得了最佳性能，表明其对于俯仰角变化的稳健性。在俯仰角差异下的情况下，SRC下的单一准则往往不能够获得可靠判决。通过三种准则的有机结合能够有效提升分类的稳健性。
表 3 俯仰角变化的实验条件
Table 3. Experimental setup under depression angle differences
Class Configuration Depression angle Training Test 17° 30° 45° 2S1 B01 299 288 303 BRDM2 E-71 298 287 303 ZSU23/4 d08 299 288 303 
图 4 不同俯仰角的结果对比
Figure 4. Result comparison at different depression angles
-
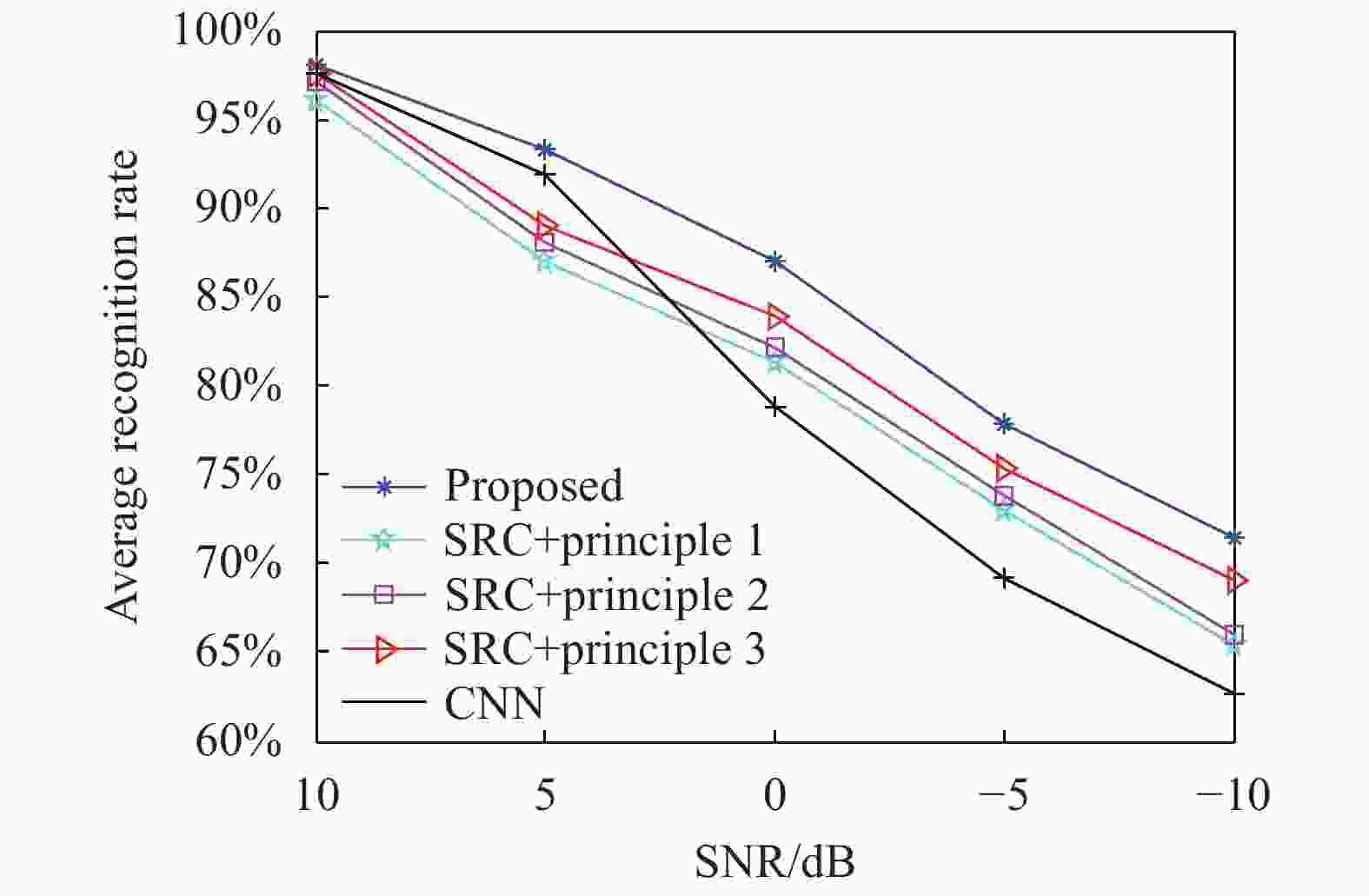
噪声存在于SAR数据获取和成像的全过程，因此是SAR图像目标识别中必须考虑的因素。随着噪声的不断加剧，原始目标特性不断被干扰甚至淹没。原始MSTAR数据集中的图像均采集自合作条件，受到噪声干扰的影响较小，信噪比（signal-to-noise ratio，SNR）较高。为此，该实验按照参考文献[10]中思路对表1中的测试样本实施噪声添加，然后利用各方法对噪声样本进行分类。图5给出不同方法的性能曲线。通过多判决准则的决策融合，文中的SRC分类结果明显优于其它三类基于单一决策准则的SRC算法，表明提出方法的有效性。综合对比所有方法，文中方法具有最强的噪声稳健性。
图 5 噪声干扰下的平均识别率
Figure 5. Avarage recognition rates under noises
-
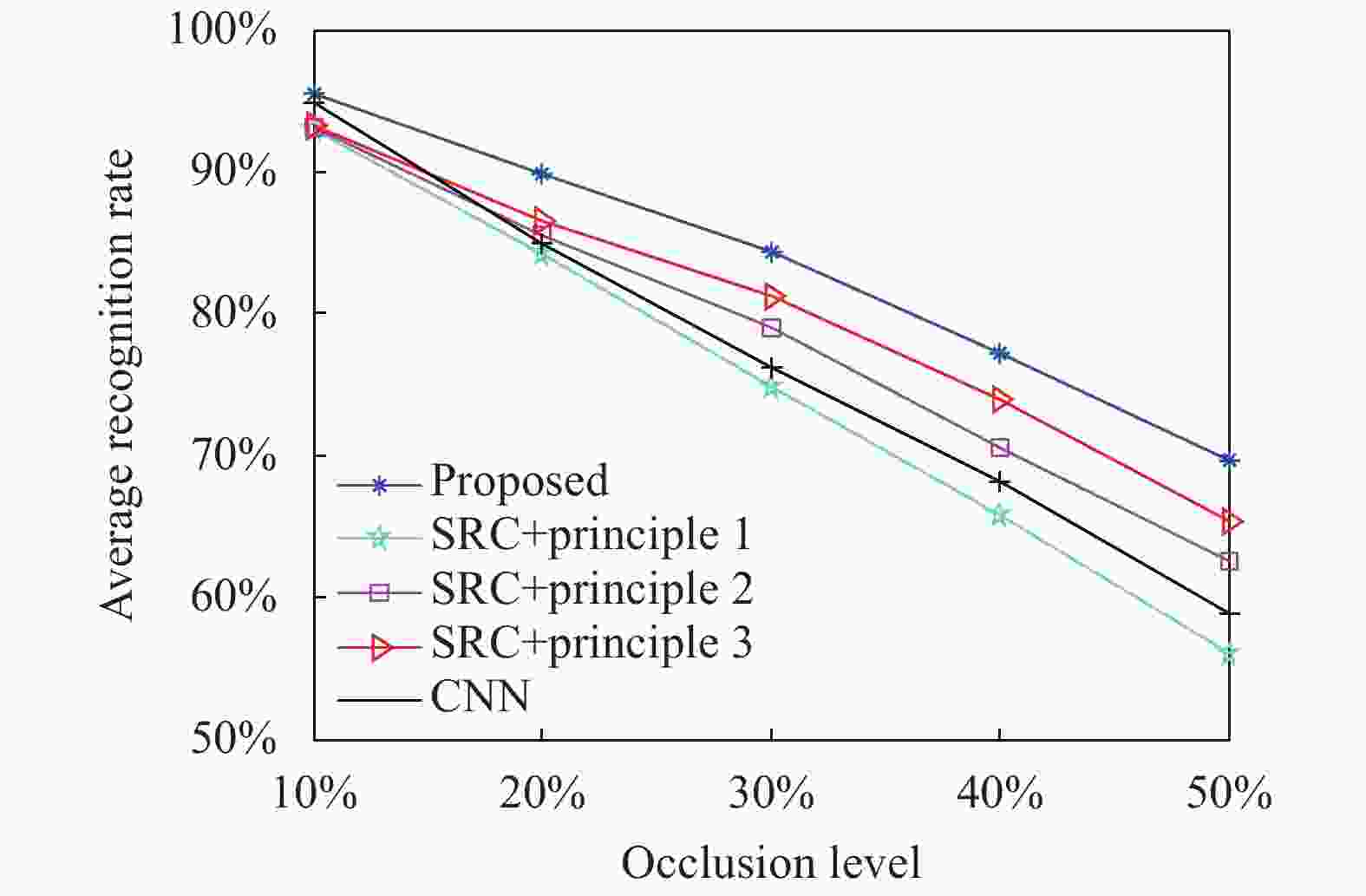
实际场景中，目标存在被障碍物遮挡的可能。因此，最终采集的SAR图像会缺失部分目标。参考文献[10, 18-19]中均对部分遮挡条件下的SAR目标识别问题展开研究。为构造部分遮挡的SAR图像测试样本，上述文献提出了SAR目标遮挡模型。文中按照相同的思路对表1中的测试样本进行不同程度的目标遮挡，然后对各类方法进行测试，得到如图6所示的性能曲线。各方法的识别率均随着遮挡比例的增大而不断减小。对比而言，文中方法对于遮挡的稳健性更强。通过结合三种决策准则，有利于提高最终决策对于目标遮挡的适应性。与CNN方法相比，基于SRC的几类方法在遮挡比例较大的情况下性能更优，也体现了稀疏表示对于目标遮挡的稳健性[16]。
图 6 目标遮挡下的平均识别率
Figure 6. Avarage recognition rates under target occlusions
-
文中提出结合多决策准则的稀疏表示分类并在SAR目标识别中进行了验证。考虑到传统SRC最小重构误差决策准则的稳健性不足，文中针对性设计了最大系数能量准则和局部最小重构误差原则。三种准则相互补充，能够更好地反映系数表示系数体现出的类别差异。为了综合三者优势，采用线性加权对它们的决策变量进行融合，获得更为可靠的识别结果。基于MSTAR数据集开展了广泛实验，通过与单一准则下的SRC分类结果对比，文中方法通过多准则的联合使用显著提高了识别的精度和稳健性；与当前流行的CNN方法相比，文中方法仍然具有性能优势。
Combination of multiple decision principles based on sparse representation-based classification for target recognition of SAR image
-
摘要: 提出组合多决策准则的稀疏表示分类（Sparse Representation-based Classification，SRC）并在合成孔径雷达（Synthetic Aperture Radar，SAR）目标识别中进行应用。传统SRC通常在全局字典上对测试样本进行重构，分别计算不同训练类别对于测试样本的重构误差，最终根据最小重构误差的原则进行分类决策。然而，由于SAR目标识别问题的复杂性，单一决策准则往往对扩展操作条件的适应性不强，导致整体性能下降。为此，文中基于稀疏表示求解的系数矢量，分别采用最小重构误差原则、最大系数能量原则以及局部最小重构误差原则分别进行分类。最小重构误差准则直接采用传统算法。最大系数能量准则分别计算不同训练类别系数能量，按照能量最大的原则进行判决。局部最小重构误差原则在局部字典上对测试样本进行表征和分析，充分体现SAR图像的视角敏感性。对于三个准则获取的决策变量，通过适当转换统一采用概率分布形式进行表达。最终，基于线性加权融合对三个准则的结果进行分析，判决测试样本所属目标类别。基于MSTAR数据集对方法进行测试，分别验证了提出方法在标准操作条件、俯仰角差异、噪声干扰及目标遮挡等情形的性能。实验结果表明：所提方法通过结合多决策准则能够有效提升SAR目标识别性能。Abstract: A synthetic aperture radar (SAR) target recognition method using multiple decision principles in sparse representation-based classification (SRC) was proposed. The traditional SRC generally reconstructed the test sample on the global dictionary and calculated the reconstruction errors of individual training classes. And the decision was reached based on the minimum reconstruction error. However, because of the complexity of SAR target recognition, a single decision principle probably had low adaptivity to the extended operating conditions (EOC). Therefore, this paper employed the global minimum reconstruction, maximum coefficient energy, and local minimum reconstruction error principles to make decisions based on the solved coefficient vector from sparse representation. The global minimum reconstruction error principle directly adopted the traditional one. The maximum coefficient energy principle calculated the coefficient energies of different classes and made decision based on the maximum one. The local minimum reconstruction error principle represented and analyzed the test sample on the local dictionary so the azimuthal sensitivity of SAR imaging could be exploited. For the decision values from the three principles, they were transformed to the same type of probability vectors. Finally, the linear fusion was performed to combine their decisions. Experiments were conducted on the MSTAR dataset under situations including the standard operating condition (SOC), depression angle variance, noise corruption, and target occlusion. The results validate that the combination of multiple decision principles could effectively improve SAR target recognition performance.
-
表 1 基于MSTAR数据集的典型实验条件示例
Table 1. Typical experimental setup based on the MSTAR dataset
Class Training Test Configuration Number of images Configuration Number of images BMP2 9 563 233 9 563 195 9 566 196 c21 196 BTR70 c71 233 c71 196 T72 132 232 132 196 812 195 s7 191 T62 A51 299 A51 273 BRDM2 E-71 298 E-71 274 BTR60 7 532 256 7 532 195 ZSU23/4 d08 299 d08 274 D7 13 015 299 13 015 274 ZIL131 E12 299 E12 274 2S1 B01 299 B01 274 
下载: 导出CSV
表 2 标准操作条件下的结果对比
Table 2. Results comparison under SOC
Method type Average recognition rate Proposed 98.52% SRC+Principle 1 96.54% SRC+Principle 2 95.88% SRC+Principle 3 97.06% CNN 98.14%
下载: 导出CSV
表 3 俯仰角变化的实验条件
Table 3. Experimental setup under depression angle differences
Class Configuration Depression angle Training Test 17° 30° 45° 2S1 B01 299 288 303 BRDM2 E-71 298 287 303 ZSU23/4 d08 299 288 303
下载: 导出CSV
-
[1] EL-darymli K, Gill E W, Mcguire P, et al. Automatic target recognition in synthetic aperture radar imagery: a state-of-the-art review [J]. IEEE Access, 2016, 4: 6014-6058. doi: 10.1109/ACCESS.2016.2611492 [2] Wen Gongjian, Zhu Guoqiang, Yin Hongcheng, et al. SAR ATR based on 3D parametric electromagnetic scattering model [J]. Journal of Radar, 2017, 6(2): 115-135. (in Chinese) [3] Mishra K. Validation of PCA and LDA for SAR ATR[C]//IEEE Tencon, 2008: 1–6. [4] Han Ping, Wang Huan. Research on the synthetic aperture radar target recognition based on KPCA and sparse representation [J]. Journal of Signal Processing, 2013, 29(13): 1696-1701. (in Chinese) [5] Cui Z Y, Cao Z J, Yang J Y, et al. Target recognition in synthetic aperture radar via non-negative matrix factorization [J]. IET Radar, Sonar and Navigation, 2015, 9(9): 1376-1385. doi: 10.1049/iet-rsn.2014.0407 [6] Dong G G, Kuang G Y, Wang N, et al. SAR target recognition via joint sparse representation of monogenic signal [J]. IEEE Journal of Selected Topics Applied Earth Observation and Remote Sensing, 2015, 8(7): 3316-3328. doi: 10.1109/JSTARS.2015.2436694 [7] Anagnostopoulos G C. SVM-based target recognition from synthetic aperture radar images using target region outline descriptors [J]. Nonlinear Analysis, 2009, 71(2): 2934-2939. [8] Zhao Pengju, Gan Kai. SAR target recognition based on hierarchical decision fusion of complementary features [J]. Electronics Optics & Control, 2018, 25(10): 28-32. (in Chinese) doi: 10.3969/j.issn.1671-637X.2018.10.006 [9] Xie Qing, Zhang Hong. Multi-level SAR image enhancement based on regularization with application to target recognition [J]. Journal of Electronic Measurement and Instrumentation, 2018, 32(9): 157-162. (in Chinese) [10] Ding Boyuan, Wen Gongjian, Yu Liansheng, et al. Matching of attributed scattering center and its application to synthetic aperture radar automatic target recognition [J]. Journal of Radar, 2017, 6(2): 157-166. (in Chinese) [11] Ding B Y, Wen G J, Zhong J R, et al. A robust similarity measure for attributed scattering center sets with application to SAR ATR [J]. Neurocomputing, 2017, 219: 130-143. doi: 10.1016/j.neucom.2016.09.007 [12] Liu H C, Li S T. Decision fusion of sparse representation and support vector machine for SAR image target recognition [J]. Neurocomputing, 2013, 113: 97-104. doi: 10.1016/j.neucom.2013.01.033 [13] Thiagaraianm J, Ramamurthy K, KneeP P, et al. Sparse representations for automatic target classification in SAR images[C]//4th Communications, Control and Signal Processing, 2010: 1–4. [14] Chen S Z, Wang H P, Xu F, et al. Target classification using the deep convolutional networks for SAR images [J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(8): 4806-4817. doi: 10.1109/TGRS.2016.2551720 [15] Zhang Panpan, Luo Haibo, Ju Moran, et al. An improved capsule and its application in target recognition of SAR images [J]. Infrared and Laser Engineering, 2020, 49(5): 20201010. (in Chinese) doi: 10.3788/irla.26_invited-zhangpanpan [16] Xu Ying, Gu Yu, Peng Dongliang, et al. SAR ATR based on disentangled representation learning generative adversarial networks and support vector machine [J]. Optics and Precision Engineering, 2020, 28(3): 727-735. (in Chinese) doi: 10.3788/OPE.20202803.0727 [17] Wright J, Yang A Y, Ganesh A, et al. Robust face recognition via sparse representation [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(2): 210-227. doi: 10.1109/TPAMI.2008.79 [18] Ding B Y, Wen G J. Exploiting multi-view SAR images for robust target recognition [J]. Remote Sensing, 2017, 9(11): 1150. doi: 10.3390/rs9111150 [19] Cai Derao, Song Yuzhen. Joint decision of multi-view SAR images with discrimination analysis with application to SAR ATR [J]. Journal of CAEIT, 2019, 14(1): 37-41. (in Chinese) doi: 10.3969/j.issn.1673-5692.2019.01.007 -
点击查看大图
图(6) / 表(3)
计量
- 文章访问数: 242
- HTML全文浏览量: 78
- PDF下载量: 22
- 被引次数: 0
