-
在大数据技术不断成熟的背景下,高速光纤传输网络成为服务器之间主要的连接方式,其高带宽、低损耗等特性非常适用于海量数据的传输[1]。但伴随着通信数据规模的激增,网络中心的带宽资源仍旧面临挑战。光纤网络的普及使越来越多的光纤跨段加入到了通信主网络中,如何实现数据流在网络中合理分配,提高网络传输利用率成为了一个重要研究议题[2-3]。因为受成本限制,无法单纯地通过增加服务器数量实现数据流量的扩容,故优化数据流路径[4]、提高通信效率[5]成为一个重要的研究方向。为了在现有光纤网络的基础上实现网络资源的最优配置,各种新型架构设计也应运而生,如拓扑结构[6]、全无线通信结构[7]、开放数据结构[8]等。
BENNER A等人研究了针对多计算机的光互联网络,并采用数据优化算法提高了数据间的流通效率,对数据流路径优化具有一定的指导意义[9]。FERNÁNDEZN等人在光网络中通过虚拟拓扑的方式完成了对网络数据资源分配的仿真分析,降低了传输数据阻塞的概率[10]。BALANICI M等人在分析混合数据传输效果的基础上,对不同数据格式数据流对传输路径的影响进行分析,为混合格式数据优化提供了新的思路[11]。陈凯等人提出了一种用于光交换网络中的数据分配算法,实现了针对数据属性的分类计算[12]。总之,目前对网络通信路径的优化研究主要集中在数据流控制、格式匹配等方面,而网络传输效率是综合作用实现的,所以,文中提出了一种基于机器学习的改进型聚类算法,首先完成数据特征获取与数据流分类的数据预处理,再将数据特征参数导入聚类算法的核函数,最终实现网络中数据传输的路径优化。
-
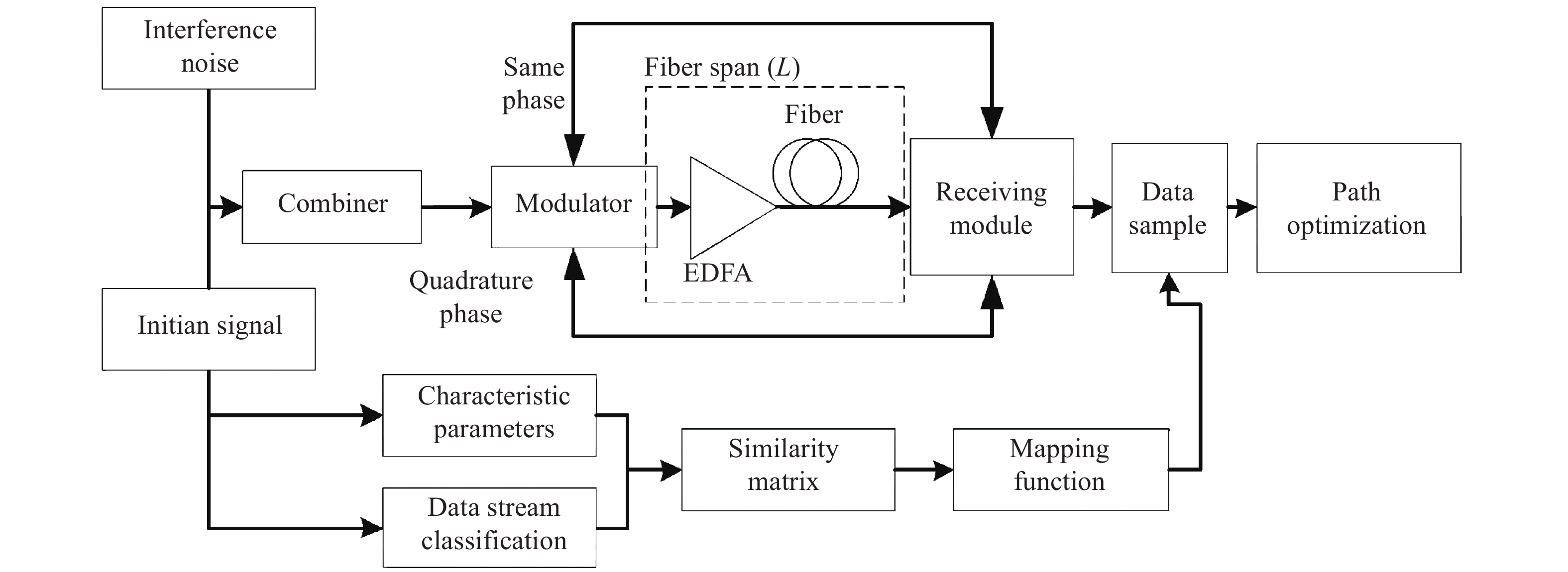
为了测试光纤网络传输效率与传输质量,搭建了包含三种主要数据流的初始信号和干扰噪声,基于机器学习的网络路径优化系统构如图1所示。由图1可以看出,为了量化干扰信号对监测信号的影响程度,采用将已知强度的干扰信号与监测信号合波进入解调器,在通过掺饵光纤放大器[13](Erbium Doped Fiber Amplifier,EDFA)和光纤跨段达到接收模块,最终通过一个移位操作运算(BV计算单元)完成数据导出。
-
在机器学习中分类器是数据分类的核心结构,而分类器中数据特征的选取直接决定了分类效果和运算的侧重。网络路径优化问题是在同一网络中能够遍历到所有网络节点,用时最少、信号能量损失最小的最优解问题。所以为了准确表示问题,采用信道发射功率(PT)表征信号能量,采用比特率(RB)和调制类型(TM)表征损耗方式,采用跨段数和跨段长度表征用时量。最终,由以上参量作为机器学习的数据特征参数。
-
为了提高网络路径优化效果,对光纤传输数据进行分类,在分析光纤跨段内数据流量的基础上构建聚类群,从而使网络可以根据当前数据流量分布调节数据路径,实现网络资源的充分利用。
对初始光纤网络数据进行K-means聚类分析[14],在基于迭代计算的方法下获得多个对象的聚类中心,再计算每个对象与聚类中心的距离,实现分段区域中距离最短数据的集合。在该网络数据中,聚类后结果可主要分为三种数据类型:(1)普通web流量(Fweb
),特点是一般访问操作,流量较少,实时性要求低,其可以作为主要的网络路径调配类型,用于与数据流量大的类型进行路径互补;(2)点对点通信流量(FP2P),特点是流量大,资源占有率大,容易造成带宽被占用而导致的网络拥堵,需要对其传输路径进行优化分配;(3)Tor流量(The Onion Router,FTor),特点是匿名传输,保证用户活动隐蔽性,其传输数据路径要求具有一定的变化性,从而保证其安全性。 由此可见,在完成路径优化过程中不但需要对数据特征参数进行选择,还需要根据数据类型的特点进行传输路径的调整,该节中的分类作为数据类型参量引入路径优化算法,从而构成边界条件的一项判断阈值。
-
依据数据特征参数建立关于数据流类型的相似度矩阵,从而将表征传输数据状态的特征参数与拟规划通信路径的数据流类型之间建立函数映射关系。则其相似度矩阵T'ij可表示为:
$$\left\{ \begin{array}{l} {T'_{ij}} = \displaystyle\sum\limits_{i = 1}^n {{P_i} \times {T_{ij}}} \\ {P_i} = k\left[ {\begin{array}{*{20}{c}} {{F_{\rm web}}}&{{F_{\rm P2P}}}&{{F_{\rm Tor}}} \end{array}} \right] \cdot\\ \;\;\;\;\;\;\;{\left[ {\begin{array}{*{20}{c}} {{P_{\rm T}}}&{{R_{\rm B}}}&{{T_{\rm M}}} \end{array}} \right]^{\rm T}} \end{array} \right.$$ (1) 式中:i, j表示数据地址序号(i=1,2,···,n; j=1,2,···,m);Pi表示包含数据特征参数及数据流类型的权重项;Ti表示地址i中的数据矩阵;k表示调节因子。
通过非线性主成分分析[15]求解该矩阵中的相似度测度(Ms),从而依据测度分布完成数据分段聚类。设拟传输的数据流样本为X(t),X(t)=x1(t), x2(t), ···, xN(t),映射函数为ω(xi(t)),将样本数据从输入空间RN映射到特征空间SN,有:
$$\omega ({x_i}(t)):{R^N} \to {S^N}$$ (2) 式中:t为某时刻值;N代表数据容量。通过映射函数可实现数据降维,结合相似性测度的分布模型对传输路径进行分段聚类。由映射函数投影后得到的样本协方差矩阵C有:
$$C = \frac{1}{n}\sum\limits_{i = 1}^N {\omega ({x_i}(t)){\omega ^{\rm T}}({x_i}(t))} $$ (3) 在此基础上,确定核函数Ki,j可表示为:
$${K_{i,j}} = C \cdot {T'_{ij}}$$ (4) 最终,利用调整核函数的反馈与迭代参数使类间距(传输路径)达到最小值,实现网络传输路径的优化。相比传统K-means聚类分析而言,改进算法将数据特征和数据流类型作为参数,克服了传统参数预设依靠经验自适应差的问题。
-
基于以上系统模型构建和核心算法调整函数推导,基于数据特征的改进聚类算法步骤如下:
(1) 对初始数据的特征参数进行提取,得到发射功率PT、比特率RB和调制类型TM的具体数值;
(2) 对不同光纤跨段的传输数据进行数据流分类,得到web流量Fweb、点对点通信流量FP2P和Tor流量FTor,从而确定传输过程中不同类型数据流在各个光纤跨段中的权重比例;
(3) 计算相似度矩阵T'ij,和相似度测度Ms;
(4) 计算映射函数ω(xi(t))和协方差矩阵C;
(5) 确定核函数Ki,j的具体函数形式;
(6) 将核函数代入所有光纤跨段数据中完成聚类运算,运算结果的每一项与判定阈值进行比较,当小于阈值时输出至同一路径优化数据集中,当大于阈值时返回聚类运算重新对比,直至所有数据均实现小于判定阈值的路径距离最优解,迭代终止,其算法流程如图2所示。
-
为了验证文中算法的网络数据传输优化性能,对包含多个光纤跨段的网络进行传输路径优化,并与不采用基于特征数据改进的传统K-means聚类算法对同一组数据进行对比。在测试过程中,分别设置了6种不同数据流占比情况。不同的分类方法的依据主要是数据流量类型的差异,将三种数据流量的占比分别以一种多而另外两种少、三种差不多以及随机分配的方式进行设置。故分别是:情况1为Fweb10%、FP2P10%和FTor80%;情况2为Fweb10%、FP2P80%和FTor10%;情况3为Fweb80%、FP2P10%和FTor10%;情况4为Fweb33%、FP2P33%和FTor34%;情况5为Fweb24%、FP2P63%和FTor13%;情况6为Fweb15%、FP2P24%和FTor61%。则对不同数据流的聚类结果进行统计,分类结果如表1所示,表中,分类正确率为Pc,假正率为Pf。
表 1 不同数据流占比条件下的数据准确率与假正率
Table 1. Data accuracy and false positive rate under the conditions of different data streams
Data flow percentage type Proposed algorithm K-means algorithm Pc Pf Pc Pf Case 1 91.6% 1.14% 80.2% 6.21% Case 2 93.4% 1.23% 83.5% 4.56% Case 3 98.2% 0.54% 98.1% 0.68% Case 4 95.4% 0.83% 89.2% 2.45% Case 5 94.7% 0.92% 85.7% 4.13% Case 6 94.1% 0.97% 84.6% 5.31% Mean 94.6% 0.94% 84.6% 3.89% 表1中分类准确率为分类正确的数据与总数据量的比,假正率为预测正确但实际错误的数据与总数据量的比(采用假正率是因为预测认为正确的值就会参加路径优化计算,而假负率虽然也是错误数据但不参与计算,故未进行统计)。由表中数据分布可知,当传输数据类型以Fweb为主时,分类准确率最差,假正率最高;当传输数据类型以FTor为主时,分类准确率最好,其对应的假正率也最低,即情况1和3所示。当FP2P和FTor占比增加时,使数据流量增大且路径变化要求提高,故导致数据聚类准确度下降,假正率增大,即情况1和2所示。当采用均匀或随机分布数据流类型时,两种算法的测试结果仍旧符合之前的变化规律,即情况4、5和6所示。综上所述,在以上6种具有一定代表性数据流分布的情况下,所提算法的分类准确率和假正率均优于传统聚类算法。
-
随着光纤跨段数量的增加,需要分析算法对数据总量的敏感程度,从而验证其在光纤网络高数据通量中的可行性。采用相同网络的数据分析时间对比了两种算法的执行时间,结果如图3所示。
由图3(a)可知,当数据包的数量不断增多时,算法完成数据分类及路径优化的执行时间会随之增加,相比而言,所提算法随着数据量增大而增加的执行时间相对缓慢,平均时间为12.8 s,优于传统K-means聚类算法的平均执行时间20.8 s。在传输数据总量固定的条件下,执行时间就是对应该传输数据量时算法的收敛时间,由此可见,随着数据量的增大所提算法的时效性更好。在对传输总量为200个数据包的聚类过程进行分析时,随执行时间的聚类变化度如图3(b)所示,该算法在超过10 s以后的变化度基本平稳,均值为31.3%,而K-means聚类算法约在14 s后趋于平稳,均值为46.2%。从聚类变化度可以验证所提算法的聚类稳定性要优于前者,同时聚类结果的平滑度也略优于前者。
-
文中为了提高光纤网络传输能效,提出了一种数据传输路径优化算法。该算法在基于机器学习数据预处理的基础上,将数据特征与数据流类型作为聚类的优化项,实现了提高传输数据分类准确率,降低平均执行时间以及增强算法稳定性的目的。与未改进的传统聚类分析算法相比,该算法在分类准确率、假正率、收敛速度以及聚类变化度方面均有一定优势,验证了其具有一定的实用意义。
An improved machine learning algorithm for optical fiber network path optimization
-
摘要: 针对光纤网络通信中数据流传输路径质量影响网络资源利用率的问题,提出了一种改进的数据传输路径优化机器学习算法。首先,利用机器学习完成对初始数据的预处理,获取数据特征信息,完成数据流分类。基于对光纤跨度内数据流的分析,构建集群组完成数据路径的调整,实现网络资源的充分利用。其次,以包含特征参数的相似矩阵为约束条件,完成聚类分析的优化。根据数据特征参数建立相似矩阵,并在特征参数与通信路径的数据流类型之间建立函数映射关系。最后利用核函数对传输路径进行优化,实现网络传输路径的优化。实验针对包含多个光纤跨度的网络进行路径优化,并与传统的K-means聚类算法对比。测试中6种不同数据流的比例可以充分反映不同条件下的数据通信状态。实验结果表明:该算法的分类准确率为94.6%,平均执行时间为12.8 s,平均聚类变化度为31.3%。传统的K-means聚类算法分类准确率为84.6%,平均执行时间为20.8 s,平均聚类变化为46.2%。该算法的收敛时间也优于传统算法,其在网络数据传输中具有更高的准确性和实时性。Abstract: Aiming at the problem that the quality of the data stream transmission path in optical fiber network communication affected the utilization of network resources, an improved data transmission path optimization machine learning algorithm was proposed. Firstly, the machine learning was used to complete the preprocessing of the initial data, the data feature information was obtained, and the data stream classification was completed. Based on the analysis of the data flow within the optical fiber span, a cluster group was constructed to complete the adjustment of the data path and realize the full use of network resources. Secondly, the optimization of the cluster analysis was completed by taking the similarity matrix containing the characteristic parameters as the constraint condition. The similarity matrix was established according to the data characteristic parameters, and the function mapping relationship was established between the characteristic parameters and the data flow type of the communication path. Finally, the kernel function was used to optimize the transmission path to realize the optimization of the network transmission path. The experiment optimized the path for a network containing multiple fiber spans, and compared it with the traditional K-means clustering algorithm. The ratio of the 6 different data streams in the test can fully reflect the data communication status under different conditions. The experimental results show that the classification accuracy of the algorithm is 94.6%, the average execution time is 12.8 s, and the average cluster change degree is 31.3%. The classification accuracy of the traditional K-means clustering algorithm is 84.6%, the average execution time is 20.8 s, and the average clustering change is 46.2%. The convergence time of this algorithm is also better than that of traditional algorithms, and it has higher accuracy and real-time performance in network data transmission.
-
表 1 不同数据流占比条件下的数据准确率与假正率
Table 1. Data accuracy and false positive rate under the conditions of different data streams
Data flow percentage type Proposed algorithm K-means algorithm Pc Pf Pc Pf Case 1 91.6% 1.14% 80.2% 6.21% Case 2 93.4% 1.23% 83.5% 4.56% Case 3 98.2% 0.54% 98.1% 0.68% Case 4 95.4% 0.83% 89.2% 2.45% Case 5 94.7% 0.92% 85.7% 4.13% Case 6 94.1% 0.97% 84.6% 5.31% Mean 94.6% 0.94% 84.6% 3.89% -
[1] Girolami M. Mecer kernel based clustering in feature space [J]. IEEE Trans on Neural Networks, 2002, 13(3): 780-784. doi: 10.1109/TNN.2002.1000150 [2] Zhang Li, Zhou Weida, Jiao Licheng. Kernel clustering algorithm [J]. Chinese Journal of Computers, 2002, 25(6): 587-590. (in Chinese) doi: 10.3321/j.issn:0254-4164.2002.06.005 [3] Ding Suijuan. Energy saving optimization simulation of mass data transmission under large data cloud storage [J]. Computer Simulation, 2018, 35(5): 160-163. (in Chinese) doi: 10.3969/j.issn.1006-9348.2018.05.033 [4] Liu Yan, Wang Cunrui. An improved big data clustering method based on sampling fusion [J]. Microelectronics & Computer, 2017, 34(4): 17-21. (in Chinese) [5] Li Jianxun, Shen Jingjing, Li Weiqian, et al. Cluster method for spatial data based on trend function [J]. Computer Engineering and Applications, 2017, 53(6): 22-28. (in Chinese) doi: 10.3778/j.issn.1002-8331.1609-0072 [6] Gu Xiaoqing, Jiang Yizhang, Wang Shitong, et al. Zero-order TSK-type fuzzy system for imbalanced data classification [J]. Acta Automatica Sinica, 2017, 43(10): 1773-1788. (in Chinese) doi: 10.16383/j.aas.2017.c160200 [7] Lu Huijuan, Liu Yaqing, Meng Yaqiong, et al. Classifier algorithm of genetic data based on kernel principal component analysis and rotation forest [J]. Journal of Frontiers of Computer Science & Technology, 2017, 11(10): 1570-1578. (in Chinese) doi: 10.3778/j.issn.1673-9418.1608046 [8] Pang Renming, Wang Bo, Ye Hao, et al. Clustering of blast furnace historical data based on PCA similarity factor and spectral clustering [J]. Journal of Shandong University(Engineering Science), 2017, 47(5): 143-149. (in Chinese) doi: 10.6040/j.issn.1672-3961.0.2017.172 [9] Benner A. Optical interconnect opportunities in supercomputers and high end computing[C]//Optical Fiber Communication Conference, Optical Society of America, 2012: OTu2B.4. [10] Fernández N, Barroso R J D, Siracusa D, et al. Virtual topology reconfiguration in optical networks by means of cognition: Evaluation and experimental validation [J]. IEEE/OSA Journal of Optical Communications and Networking, 2015, 7(1): 162-173. doi: 10.1364/JOCN.7.00A162 [11] Balanici M, Pachnicke S. Hybrid electro-optical intra-data center networks tailored for different traffic classes [J]. IEEE/OSA Journal of Optical Communications and Networking, 2018, 10(11): 889-901. doi: 10.1364/JOCN.10.000889 [12] Chen Kai, Singla Ankit, Singh Atul, et al. An optical switching architecture for data center networks with unprecedented flexibility [J]. IEEE/ACM Transactions on Networking, 2014, 22(2): 498-511. doi: 10.1109/TNET.2013.2253120 [13] Liu Nian, Zhang Qingxin, Li Xiaofang. Distributed photovoltaic short-term power output forecasting based on extreme learning machine with kernel [J]. Transactions of the Chinese Society of Agricultural Engineering, 2014, 30(4): 152-159. (in Chinese) doi: 10.3969/j.issn.1002-6819.2014.04.019 [14] Fan Geng, Ma Dengwu, Deng Li, et al. Fault prognostic model based on grey relevance vector machine [J]. Systems Engineering and Electronics, 2012, 34(2): 424-428. (in Chinese) doi: 10.3969/j.issn.1001-506X.2012.02.39 [15] Roberto Perdisci, Giorgio Giacinto, Fabio Roli. Alarmclustering for intrusion detection systems in computer networks [J]. Engineering Applications of Artificial Intelligence, 2006, 19(4): 429-438. doi: 10.1016/j.engappai.2006.01.003 -







 下载:
下载: