-
众所周知光是一种横波,具有偏振特性。偏振现象最早可以追溯到1669年Bartholinus首次发现的晶体双折射。然而,人们真正认识到偏振则归功于 Fresnel,他从横波观点出发,说明光的偏振并据此解释了旋光现象。1864年,Maxwell建立著名的电磁场方程组并预言了电磁波的存在,理论诠释了光的偏振。对于传统光束而言,其偏振态为空间均匀分布,例如线偏振、圆偏振、椭圆偏振等。20世纪60年代,科学家们从理论上提出了两种偏振态非均匀分布的矢量光场——径向偏振场光场和旋向偏振光场[1]。然而实验上产生这两种光场却在激光发明之后的20世纪70年代。Mushiake等[2]在激光谐振腔内设计了一种特殊的光学振荡器,实验输出径向偏振光场;Pohl等[3]利用谐振腔中的偏振模式选择器产生了旋向偏振光场。最初,矢量光场大多在激光器内部产生[2-3],后来逐渐发展出通过全息图[4]、干涉仪[5]和液晶器件[6]等产生矢量光场的技术。
早期矢量光的研究多集中在产生和制备,直到2000年,Rochester大学Brown研究组[7]对径向和旋向矢量光紧聚焦特性的研究使人们对矢量光场有了全新的认识。他们指出径向矢量光经过紧聚焦得到很强的纵向电场分布,这在标量光场中无法实现。Dorn等[8]实验上得到了最小尺度达0.161λ2的聚焦光斑,远小于相同条件下线偏振聚焦光斑。2002年,詹其文团队[9]将紧聚焦特性推广到任意形式的柱矢量,给出了对聚焦场调控的方法。聚焦矢量场研究的不断进步也促进着矢量光场应用领域的不断扩展,尤其是在光操控和激光加工领域。Sato等[10]验证了径向矢量偏振光在轴向捕获的优势,旋向矢量光在横向捕获上效率更高。Meier等[11]发现在切割金属时,径向偏振光的切割效率比线偏振光和圆偏振光高1.5~2倍。2009年,詹其文[12]对柱对称矢量光的概念及应用做了全面的综述,矢量光场的研究进入快速发展时期。由于其独特的偏振特性,矢量光场在微纳粒子操控[10]、材料科学[13]、高分辨成像[14]、光通信[15]、激光加工[11]和粒子加速[16]等领域都有着重要作用。
Stokes参量是描述矢量光场偏振最重要的方法,利用Stokes参量绘制的Poincaré球面可以直观地展示矢量光场的偏振状态。Poincaré球面上的点代表不同的偏振状态,对于空间均匀的偏振光,其偏振态为球面上某一点;对于早期发现的柱矢量光场,其偏振态为球面上的赤道。若能创建一种偏振状态可以覆盖整个Poincaré球的矢量光束,便可大大提高光场偏振调控的灵活性,增强光子器件和光学系统的功能和能力。2010年,王慧田课题组[17]和Brown研究组[18]分别独立构建了满足该条件的奇异光束——杂化矢量光或全庞加莱光(FP光)。从某种意义上讲,FP光束属于杂化矢量光的子集。杂化矢量光场横截面的偏振分布随角向和径向多维度变化,在单光束中遍历所有的偏振状态,无法用Poincaré球上的单一点描述。文双春和罗海陆课题组[19]于2015年推广了普通Poincaré球的概念,提出杂化Poincaré球(HyOPS)。HyOPS上每一点都可代表一种杂化矢量光,可用于分析杂化矢量光的奇异性和Pancharatnam–Berry(PB)几何相位[20-22]。由于杂化矢量光具有丰富的偏振信息,所以在传播、聚焦、非线性光学等方面表现出不同的光学效应[23-26]。目前,杂化矢量光在三维微纳粒子捕获[27]及大气湍流光束传播[28]中都表现出潜在的应用前景。因此,研究杂化矢量光具有重要的物理意义,文中将从理论、制备、特性及相关应用等方面综述近年来杂化矢量光的研究进展。
-
理论上,杂化矢量光通常由两种携带不同轨道角动量的正交偏振光叠加构成。普遍意义的杂化矢量光可以表示为:
$$\vec E(\rho ,\varphi ) = A{E_{{l_1}}}(\rho ,\varphi ){\hat e_1} + B{E_{{l_2}}}(\rho ,\varphi ){\hat e_2}$$ (1) 式中:ρ, φ, z分别代表柱坐标系的坐标;
${\hat e_1}$ 和${\hat e_2}$ 分别代表两个正交偏振的单位矢量;A和B为光场轮廓参数;${E_{{l_1}}}(\rho ,\varphi )$ 和${E_{{l_2}}}(\rho ,\varphi )$ 分别代表携带轨道角动量为l1和l2的光束,其形式取决于具体实现方式。2010年,王慧田课题组[17]采用两束携带±1的轨道角动量涡旋光场实现杂化矢量光场,公式(1)写为:
$$\vec E(\rho ,\varphi ) = \exp (i\varphi ){\hat e_1} + \exp ( - i\varphi ){\hat e_2}$$ (2) 式中:
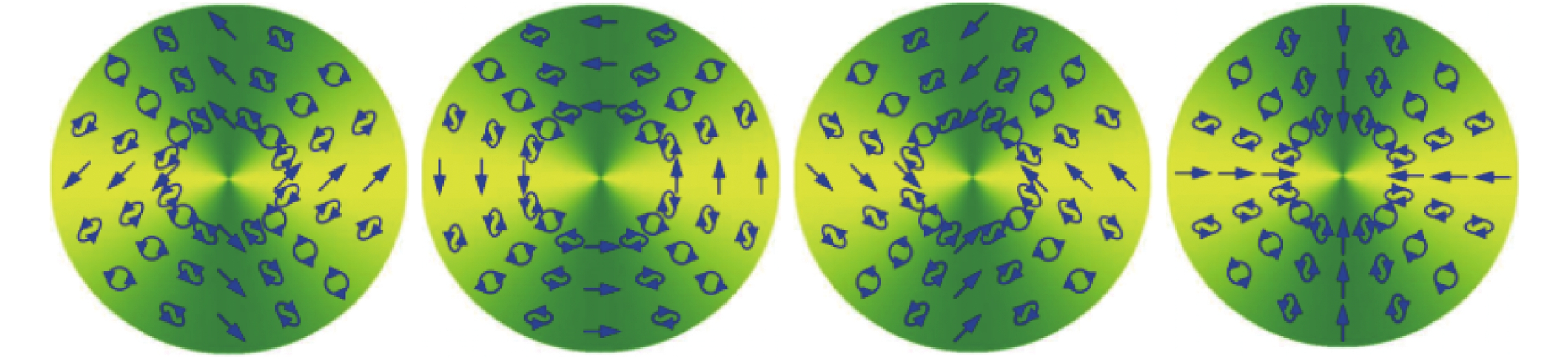
${\hat e_1} = (\cos \phi ,\sin \phi )$ 与${\hat e_2} = ( - \sin \phi ,\cos \phi )$ 由水平和垂直基矢旋转得到,$\phi $ 为其旋转角度。不同$\phi $ 对应的偏振分布如图1所示。同一年,Brown课题组[18]采用高阶Laguerre-Gauss(LG)光束与基模高斯光叠加实现另一种杂化矢量光——FP光,相应地,公式(1)可以写为:$$\vec E(\rho ,\varphi ) = {{LG}}_0^0(\rho ,\varphi ){\hat e_1} + {{LG}}_0^l(\rho ,\varphi ){\hat e_2}$$ (3) 其中,LG光束可以描述为:
$$LG_0^l(r,\varphi ) = {E_0}{r^l}L_0^l\left(\frac{{2r}}{{{w^2}}}\right)\exp \left( - \frac{{{r^2}}}{{{w^2}}}\right)\exp (il\varphi )$$ (4) 式中:φ为方位角;w为束腰;
$ L{G}_{0}^{l}(·)$ 为相关的拉盖尔多项式。不同${\hat e_1}$ 和${\hat e_2}$ 组合下全庞加莱光的偏振分布如图2所示。
图 2 (a)
${\hat e_1} = (1,i)$ 和${\hat e_2} = (1, - i)$ 、(b)${\hat e_1} = (1, - i)$ 和${\hat e_2} = (1,i)$ 、(c)${\hat e_1} = (1,0)$ 和${\hat e_2} = (0,1)$ 时,FP光束的偏振分布[18]Figure 2. Distribution of polarization for FP beams where
${\hat e_1}$ and${\hat e_2}$ are, respectively, (a)${\hat e_1} = (1,i)$ ,${\hat e_2} = (1, - i)$ ; (b)${\hat e_1} = (1, - i)$ ,${\hat e_2} = (1,i)$ ; (c)${\hat e_1} = (1,0)$ ,${\hat e_2} = (0,1)$ [18]除了LG光束,其他携带轨道角动量的光束叠加也可以实现杂化矢量光,例如2013年,Cardano等[29]通过超几何高斯光产生的杂化矢量光场可以表示为:
$$\vec E\left( {\rho ,\varphi } \right) = HyG{G_{ - |l|,l}}\left( \rho \right)[A{\hat e_{{L}}} + B\exp \left( {2il\varphi } \right){\hat e_R}]$$ (5) 这里,HyGGpm为超几何高斯光束:
$$HyG{G_{pm}} = {C_{pm}}\frac{{\varGamma (1 + |m| + p/2)}}{{\varGamma (|m| + 1)}}{i^{|m| + 1}}{\left(\frac{{\textit{z}}}{{{{\textit{z}}_R}}}\right)^{p/2}}{\left(\frac{{\textit{z}}}{{{{\textit{z}}_R}}} + i\right)^{ - [1 + |m| + p/2]}}{\rho ^{|m|}}{{\rm{e}}^{ - i{r^2}/{w^2}(\zeta + i)}}{{\rm{e}}^{im\varphi }}{}_1{F_1}\left( - \frac{p}{2},|m| + 1;\dfrac{{{\textit{z}}_R^2{r^2}}}{{{w^2}{\textit{z}}({\textit{z}} + i{{\textit{z}}_R})}}\right)$$ (6) 式中:
$\varGamma ()$ 为伽马函数;$_1{F_1}()$ 为合流超几何函数;w为束腰;${{\textit{z}}_R}$ 为瑞利范围。2015年,Shvedov等[30]基于Bessel光束产生杂化矢量光场:$$\vec E\left( {\rho ,\varphi } \right) = A{J_{|{l_1}|}}\left( {{k_\rho }\rho } \right)\exp \left( {i{l_1}\varphi } \right){\hat e_{\rm{L}}} + B{J_{|{l_2}|}}\left( {{k_\rho }\rho } \right)\exp \left( {i{l_2}\varphi } \right){\hat e_R}$$ (7) 式中:
$ {J}_{\left|l\right|}(·)$ 为一类Bessel函数。2016年,Garcia-Gracia等[31]通过Mathieu光束产生杂化矢量光:$$\vec E\left( {\rho ,\varphi } \right) = {\rm{MB}}{}_0^e\left( {\rho ,\varphi } \right){\hat e_L} + {\rm{HMB}}_l^ \pm \left( {\rho ,\varphi } \right){\hat e_R}$$ (8) 式中:MB和HM代表不同的Mathieu光束。
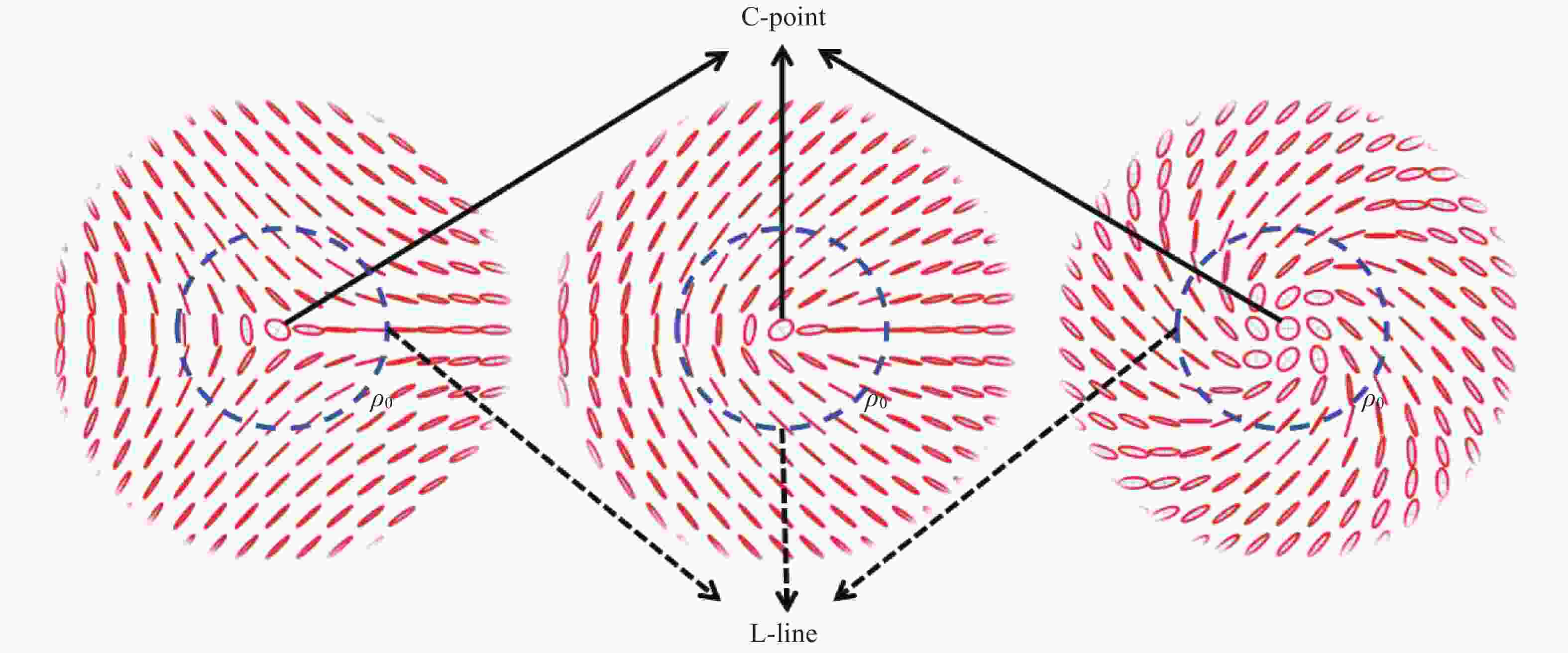
尽管杂化矢量光可以通过不同形式的光束实现,但是其偏振存在一定的相似性。这种相似性反应在偏振奇异性上。Nye[32]在1983年提出偏振奇异性的概念,Dennis[33]在2002年对光场的奇异性做了详细的综述。偏振奇异性包括偏振取向的不确定性——C点和偏振旋向的不确定性——L线。C点偏振奇异性一般用C点指数IC描述。IC定义为线积分[29]:
$${I_{\rm{C}}} = \frac{1}{{2\pi }}\oint_L {{\rm{d}}R \cdot \nabla {\gamma _0}} $$ (9) 式中:γ0
为相位分布;L为绕C点的闭合曲线。杂化矢量光比柱矢量光场具有更为丰富的C点奇异性。一般柱矢量光场C点指数的大小为±1/2,而杂化矢量光为1/2的整数倍。杂化矢量光的C点附近偏振态椭圆半长轴构成一簇围绕C点的流线。不同的C点指数对应不同形状流线:对于IC=1/2的C点,构成星形流线;对于IC=−1/2的C点,构成分柠檬形或变种星形流线;对于IC =1的C点,构成螺旋形流线,如图3所示[29]。杂化矢量光的IC 只取决于基矢光携带的轨道角动量,与具体光束类型无关。从某种意义上讲,这是因为携带相同角动量的杂化矢量光的Stokes参数在统计上是不变的,与具体光束形式无关[34]。 与C点丰富的拓扑结构相比,L线的拓扑性比较单一,没有复杂的类型划分。如图3所示[29],通常杂化矢量光的L线是闭合同心圆环,其半径与光场轮廓参数A、B有关,与携带轨道角动量和具体光束类型无关。
-
杂化矢量光的实验产生方法主要有两种:一种是双光束叠加法,对两束正交偏振光分别进行相位调制和幅度调制,然后采用干涉叠加的方法合成杂化矢量光;一种是单光束调制法,利用光场调制器件,如空间光调制器(Spatial Light Modulator, SLM)、Q板(Q-plate)、电介超表面结构、电介光栅等,对单光束的偏振和相位同时调制。
-
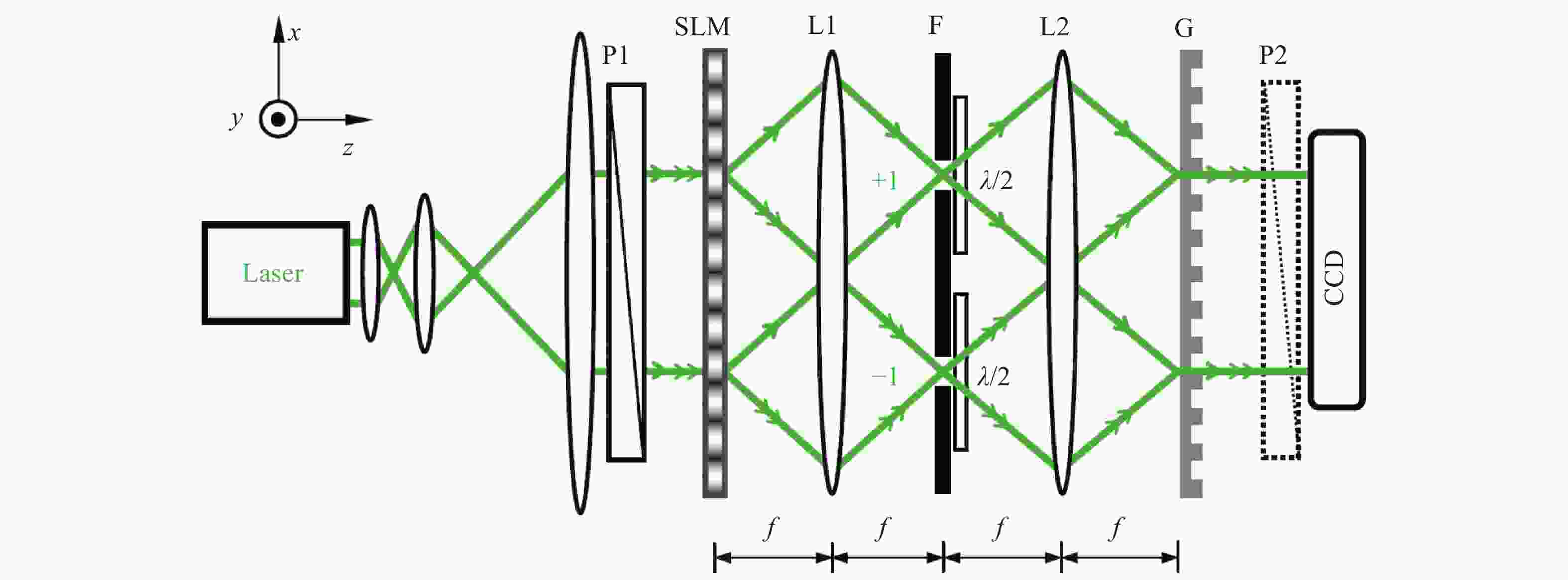
双光束干涉叠加法包括共轴干涉和离轴干涉。如图4所示,2010年王慧田课题组[17]在4f系统中利用SLM设计共轴相干光路,借助SLM在其+1和−1级衍射场获得具有相反拓扑荷的轨道角动量光,分别经过不同λ/2波片调制为正交线偏涡旋光,最后通过Ronchi相位光栅(G)实现两模式的合束叠加,首次获得偏振非均匀分布的杂化矢量光场。2017年,高春清课题组[35]调整此方案,利用反射型SLM输出两束具有不同拓扑荷的水平偏振涡旋光,半波片HWP将其中一束调制为垂直偏振,并用沃拉斯顿棱镜WP代替Ronchi相位光栅实现两正交模式的合束叠加,装置图如图5所示。2020年,赵建林课题组[36]巧妙地设计了一种共路径干涉法,对正交基矢量进行角幅度调制,得到具有方位极化梯度的杂化矢量光。
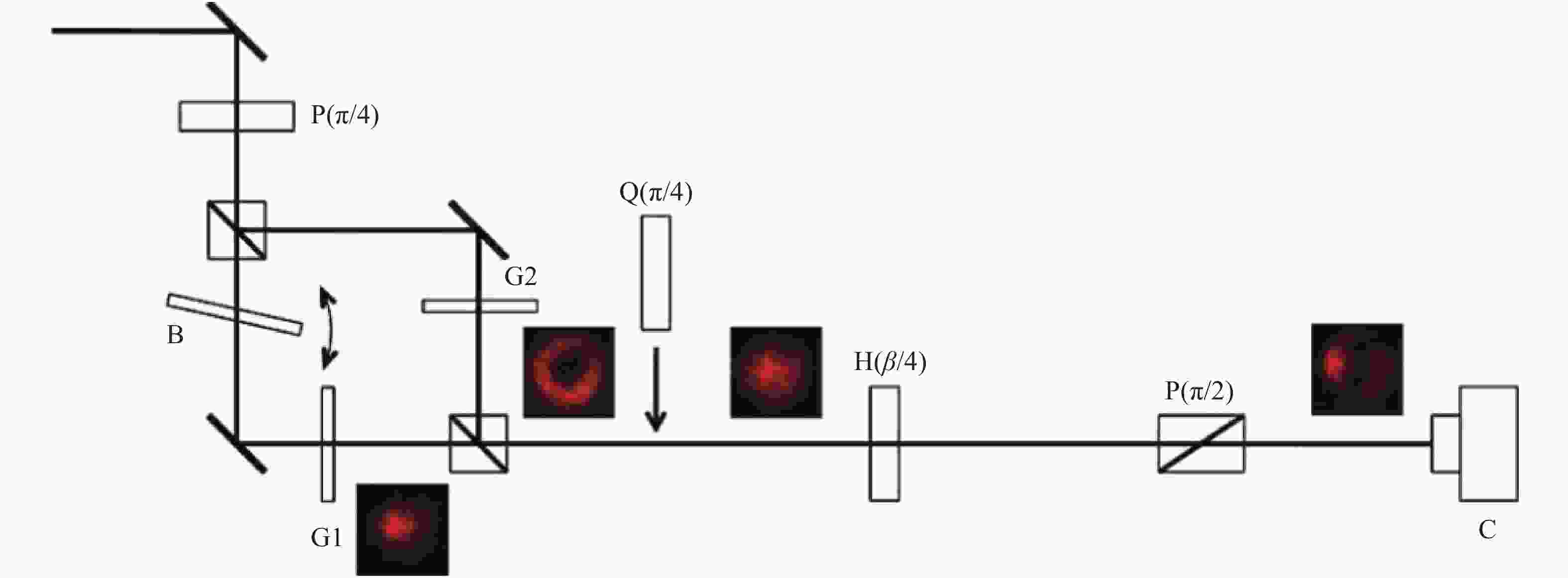
由于共轴干涉对光路要求较高,因而一部分研究人员受干涉仪的启发设计了离轴干涉方案。2012年,Galvez等[37]利用双臂中均带有叉形光栅的Mach-Zehnder干涉装置制备了Poincaré光束。如图6所示,偏振分束器分开的两束正交线偏振光分别进入干涉的两臂,经过两臂中的叉形光栅形成正交线偏振涡旋光,在第二个偏振分束器叠加形成杂化矢量光。基于该方案,2016年,Lu等 [38]用Dove棱镜代替叉形光栅,产生的杂化矢量光光强分布呈现花瓣状;2017年,Wang等[39]利用SLM代替叉形光栅,使正交偏振的高斯光与任意轨道角动量的涡旋光叠加,得到任意阶FP光束。除了Mach-Zehnder干涉装置,Sagnac干涉装置也常用于杂化矢量光的制备。2016年,Ling等 [40]利用SLM、偏振分束器PBS和反射镜M组合形成Sagnac干涉装置,如图7所示。经过半波片HWP1、格兰棱镜GLP和四分之一波片QWP1共同调制后得到的任意单一偏振光,被偏振分束器PBS分为水平偏振透射光和垂直偏振反射光。其中,水平偏振光通过SLM加载螺旋相位,经过反射镜M反射后与垂直偏振高斯光叠加,得到FP光束。2019年,袁操今小组[41-42]在SLM上加载两种不同涡旋光,采用Sagnac装置获得完美同心庞加莱光束。
-
伴随着双光束叠加法,对单一光束进行调制并产生混合矢量光的工作也逐一涌现。早期,单光束调制法主要是利用具有特殊折射率分布的热应力玻璃实现相位和强度调制,从而得到杂化矢量光。例如Brown研究组产生FP光束[18]和部分FP光束[43]均基于热应力玻璃。目前,利用液晶器件对单光束进行调制成为制备杂化矢量光的热门方法。液晶器件分为透射式和反射式两种,透射式以Q板(Q-plate)为代表,反射式以SLM为代表。
Q板是由液晶分子构成的一种特殊的各向异性双折射相位板[44]。2013年,Cardano等人[29]利用Q板将左/右旋圆偏振光调制为偏振可覆盖庞加莱球的奇异光束,该光束由携带不同轨道角动量的正交偏振分量组成。装置图如图8所示,插图显示了由q = 1/2, −1/2, 1的Q板产生的柠檬形光束、星形光束和螺旋形光束的强度分布和偏振分布。2017年,湖南大学文双春课题组[45] 对该装置进行改进,利用Q板和螺旋相位板组合,将椭圆基模高斯光调制为基模高斯光和高阶拉盖尔高斯光的叠加态,在HyOPS上实现了任意FP光束的产生。装置如图9所示,线偏振高斯光束依次通过格兰棱镜GLP1、四分之一波片QWP1和Q板(QP)产生普通矢量光束,然后再通过螺旋相位板(SPP)加载轨道角动量将普通矢量光束转化为杂化矢量光场。2019年,他们改变实验装置,利用电控Q板获得任意阶杂化矢量光束[46]。2020年,陆延青课题组[47]采用Dammann涡旋Q板多通道产生了杂化矢量光。通过调节入射偏振,最多可以在HyOPS上同时获得24个不同模式的杂化矢量光。
SLM是一种像素化的液晶显示器,每个像素都能独立调控反射光场的相位或振幅。2015年,Khajavi等[48]利用半波片调制光束的偏振,使其既有水平分量又有垂直分量,两个SLM则分别对水平和垂直分量进行相位调制,使其成为具有不同轨道角动量的涡旋光,最终产生任意Poincaré光束。Alpmann等[49]简化该装置,仅用一个SLM加载两种不同涡旋相位全息图,利用波片和反射镜控制光束的偏振和角度,使得具有正交线偏分量的光先后入射到SLM上不同位置,加载不同轨道角动量,最终获得杂化矢量光。除此以外,Otte等[50]利用SLM研究矢量光场偏振奇异性的同时,发现高阶庞加莱球矢量光在空间传输过程中也可以产生杂化矢量光,其偏振分布取决于传播距离。
除了液晶器件,近年来也有一些研究人员开始利用特殊结构器件调制单光束制备杂化矢量光。Lerman等[51]利用空间变换的亚波长电介光栅和可旋转四分之一波片组合得到杂化矢量光。文双春课题组[52]将具有可调谐性的液晶与介电超表面结合,通过控制加载在液晶相位延迟器上的电压实现任意杂化矢量光。最近,Lin等[53]讨论了基于微腔的生成方案,利用光在硅微环腔中传播时自旋自由度和轨道自由度之间的耦合形成FP光。此外,陆延青课题组[54]基于全介电超表面宽带生成完美庞加莱光,装置图如图10所示。经过声光可调谐滤波器(AOTF)系统过滤后的超连续激光通过线性偏振器(LP)和四分之一波片(QWP)转换成所需的偏振光并入射到超表面形成完美庞加莱光,透射光经过线性偏振器(LP)过滤后被捕获。
-
矢量光的聚焦特性可以用Richards-Wolf矢量衍射方法进行数值分析。对于沿着z轴传播的光束而言,焦平面附近的光场可以表示为[9]:
$$ {\vec E(r,\phi ,{\textit{z}}) = \dfrac{{ikf{{\rm{e}}^{ - ikf}}}}{{2\pi }}\displaystyle\int\limits_0^{{\theta _{\max }}} {{\rm{d}}\theta \displaystyle\int\limits_0^{2\pi } {{\rm{d}}\varphi [} } ({E_\varphi }{{\overset{\frown} {\rm{e}}} _\varphi } + {E_\rho }{{\overset{\frown} {\rm{e}}} _\rho }){ {\rm e}^{i\overrightarrow k \cdot \overrightarrow r }}\sin \theta \sqrt {\cos \theta }]} $$ (10) 式中:Eφ和Eρ为入瞳处矢量光的角向和径向分量;θmax是由透镜数值孔径决定的最大角度;k是波矢。
Brown研究组[7]发现相对于均匀偏振分布的光束,径向偏振的柱矢量在紧聚焦过程中产生更强的纵向电场,而角向偏振的柱矢量光在紧聚焦区域则不存在纵向电场。Wang等[55]利用二元环状光学器件对径向柱矢量光进行紧聚焦,产生一个超长“光针”聚焦分布,经过参数优化后获得超衍射极限的光针。除此之外,利用紧聚焦柱矢量光束还可以激发纳米天线中等离激元,在定制等离子纳米天线的光散射方面具有巨大的应用潜力[56]。
杂化矢量光的紧聚焦场比柱矢量光场的行为更为丰富。在聚焦场中心附近,偏振椭圆的取向不再局限于x-y平面,大部分沿z轴方向,场强存在较强z分量,如图11所示[24]。沿z轴方向的偏振椭圆导致其自旋方向垂直于z轴,即横向自旋[57-58]。横向自旋是自旋—轨道角动量守恒的结论,它的大小取决于入瞳处偏振椭圆的椭圆率和椭圆取向。
此外,聚焦杂化矢量光场的纵向光强分布也十分有趣。2017年,满忠胜课题组[59]对任意偏振态的光束聚焦特性进行分析,提出了通过控制正交线偏振基模实现聚焦整形的方法。2018年,詹其文团队[60]指出低数值孔径聚焦的杂化矢量光场可以在焦平面上形成一个柱对称的阶跃光强分布,通过对杂化矢量光参数的控制可以实现阶跃光场定制化。同年,李艳秋课题组[61]分析了FP光束在紧聚焦条件下的光强与纵向电场相位分布,证明了纵向电场具有轨道角动量分布。2019年,笔者与陈理想课题组[27]分析了紧聚焦下杂化矢量纵向光强对称性与其阶次之间的关系,给出光强分布图样具有m−n+2重轴对称性,m和n代表轨道角动量,具体如图12所示。
杂化矢量光场独特的聚焦特性使其在光学捕获方面更具优势。2012年,Wang[62]发现在光束截面,FP光对瑞利粒子表现为指向光束中心的力场,能将微粒束缚在光束中心。2018年,Xue等[63]指出,聚焦的杂化矢量光在束腰处的光力更为稳定,而且可以克服热运动的影响。2019年,笔者与陈理想课题组[27]研究了强聚焦情况下杂化矢量光的光力行为,发现微粒可在多个位置被捕获,捕获位置的数量取决于携带轨道角动量的值,这恰好与聚焦光场光强分布对应。除此之外,聚焦杂化矢量光场还可以将微粒限制在焦平面附近,有效地实现三维捕获。
-
在实际大气中传播时,由于大气不均匀分布、气流、湍流等对激光光强产生负面影响,引起光强闪烁。2015年,Wei等[28]通过调节杂化矢量光光场轮廓参数的比值大幅降低了光束经过湍流时的闪烁现象。相比于高斯光束或LG光束,杂化矢量光在减弱湍流引起的闪烁具有明显优势,为大气激光通讯、激光武器、激光遥感等应用奠定基础。
实际上,杂化矢量光在自由空间传输时,偏振模式和Gouy相位相关。对于正交圆偏振LG光产生的杂化矢量光而言,Gouy相位为φ=(lR-lL)arctanz/ZR,其中,lR和lL分别为右旋LG光和左旋LG的轨道角动量。随着传输距离z的增加,Gouy相位发生改变,导致偏振产生一个正比于Gouy相位的旋转[64]。旋转方向取决于(lR-lL)的正负,若为正值时,旋转方向是逆时针;若为负值时,旋转方向为顺时针。因此,Arora等[20]提出可以通过杂化矢量光传输时的旋转方向判断轨道角动量的正负。
-
杂化矢量光的非线性光学效应亦是一个非常有意义的课题。早期关于非线性光学效应的工作不涉及频率转换。例如2014年,陈理想课题组[65]报道了杂化矢量光的电光效应。经过电光效应的杂化矢量光在自由空间传播过程中,其C点和L线会产生分裂,分裂行为与细胞核和细胞质的分裂相似。直到2018年,涉及频率转换的非线性光学效应研究出现。笔者与陈理想课题组[26]利用相位匹配导致倍频光束输出单一偏振这一特性,通过倍频将杂化矢量光不可见的偏振拓扑结构可视化。由于大多数非线性过程具有偏振敏感性,因此杂化矢量光的非线性频率转换具有挑战性。2019年,笔者[25]从相位匹配输出单一线偏振光出发,提出利用正交级连晶体装置对FP光进行倍频,不仅在频率加倍的同时保留了光束的偏振特性,而且实现了拓扑荷的加倍,使其呈现出新的流线形状,图13给出了星形流线的FP光在倍频后转化为螺旋形流线。同年,Yang等[66]引入Sagnac干涉仪实现正交偏振倍频矢量光叠加,从而得到倍频的杂化矢量光。接着,基于Yang等人的装置,朱智涵课题组[67]提出自锁干涉仪,得到倍频后的杂化矢量光,同时发现倍频矢量光的C点在衍射传播中具有旋转效应。2020年,基于同样装置,他们[68]在II类相位匹配的长周期极化晶体PPKTP中实现了参量上转换,在频率转换的同时,保证杂化矢量光的偏振模式不变性。他们的结果为基于矢量模式的高维量子或高容量经典信道接口奠定了基础。2021年,Silva等[69]基于正交级连晶体的装置研究了杂化矢量光的参量下转换。泵浦光和信号光中有一束为杂化矢量光而另外一束为线偏振光时,可以输出与输入偏振一致的杂化矢量光。
除了频率转换,另一个有趣的非线性光场效应是偏振旋转。由于Gouy相位的影响,杂化矢量光在自由空间传播时存在一定的偏振旋转,但是这个旋转角度有限。2020年,东南大学顾兵课题组[70]发现FP光束经过各向同性的Kerr介质会出现整体偏振旋转。对于各向异性的Kerr介质,FP光束在传播过程中,光强图样由中心亮斑围绕的衍射环变成椭圆结构并伴随着两段衍射环。这主要是由于各向异性介质导致柠檬形FP光具有空间结构的非线性相移,这种相移来自于两个幅度不相等的左旋和右旋分量,最终引起光强图样和偏振分布出现了对称性破缺。除了Kerr介质,西安交通大学李福利课题组[71-72]发现杂化矢量光在铷原子蒸汽中也会发生偏振旋转。由于原子蒸汽对光子的吸收和激发,在原子蒸汽中传播时,杂化矢量光偏振旋转角则可以突破Gouy相位导致偏振旋转的极限。通过调节原子的相关参数可以实现任意偏振旋转角的控制,这对于偏振控制具有潜在的应用价值。
-
杂化矢量光作为一种特殊的矢量光场具有独特的偏振特性,自2010年被提出以来引起研究人员的广泛关注。文中简要回顾了杂化矢量光场的重要研究进展,包括理论模型、制备、以及其在聚焦、传播、非线性光学效应等方面的特性和应用。目前,杂化矢量光的产生方法已经成熟,然而其特性仍在研究阶段,诸如杂化矢量光和频、差频、参量转换等非线性光学效应、杂化矢量光传播过程中偏振奇异性的拓扑结构等都是十分有趣的研究方向,因此在这个领域会出现许多新现象、新想法。新特性的出现必然会伴随新应用的诞生,未来杂化矢量光的研究将逐渐从理论转向应用,这与学术兴趣和技术发展导向直接相关,在今后一段时间内都将是一个值得关注的课题。
Research progress of hybrid vector beams (Invited)
-
摘要: 偏振是光场的一个重要矢量属性。依据空间偏振分布的不同,可以将光场分为标量光场和矢量光场。其中,非均匀偏振分布的矢量光场在光场传播、聚焦、非线性效应等方面表现出一系列有趣的行为,对其进行深入研究具有重要的科学意义和应用价值。一种在同一波阵面上包含不同偏振态的杂化矢量光场,因其比普通矢量光场具有更丰富的偏振特性,自2010年被发现以来,在光通信、光学操控、量子通信等领域中展现诸多诱人的前景,目前已成为光学领域的一个研究热点。综述着重介绍了杂化矢量光的制备以及其在聚焦、传播和非线性光学等方面中的特性和应用。Abstract: Polarization is an important property of light field. According to the spatial polarization distribution, optical field can be divided into the scalar field and the vector field. Since the vector field with inhomogeneous polarization distribution performs some interesting behaviors in light propagation, studying the vector beam is of either scientific significance or engineering applied importance. The hybrid vector beams, which contains all kinds of polarization state in the same wave front, has attracted a lot of interests since 2010. Due to the richer polarization states than the normal vector beam, the hybrid vector beam shows attractive prospect on the optical communication, optical manipulation and quantum communication fields. Here, the generation, focusing, propagating and nonlinear optics of the hybrid vector beam were summarized.
-
Key words:
- hybrid vector beams /
- polarization singularity /
- full Poincaré beams /
- Poincaré sphere
-
图 2 (a)
${\hat e_1} = (1,i)$ 和${\hat e_2} = (1, - i)$ 、(b)${\hat e_1} = (1, - i)$ 和${\hat e_2} = (1,i)$ 、(c)${\hat e_1} = (1,0)$ 和${\hat e_2} = (0,1)$ 时,FP光束的偏振分布[18]Figure 2. Distribution of polarization for FP beams where
${\hat e_1}$ and${\hat e_2}$ are, respectively, (a)${\hat e_1} = (1,i)$ ,${\hat e_2} = (1, - i)$ ; (b)${\hat e_1} = (1, - i)$ ,${\hat e_2} = (1,i)$ ; (c)${\hat e_1} = (1,0)$ ,${\hat e_2} = (0,1)$ [18] -
[1] Snitzer E. Cylindrical dielectric waveguide modes [J]. Journal of the Optical Society of America A, 1961, 51(5): 491-498. doi: 10.1364/JOSA.51.000491 [2] Mushiake Y, Matsumura K, Nakajima N. Generation of radially polarized optical beam mode by laser oscillation [J]. Proceedings of the IEEE, 1972, 60(9): 1107-1109. doi: 10.1109/PROC.1972.8865 [3] Pohl D. Operation of a ruby laser in the purely transverse electric mode TE01 [J]. Applied Physics Letters, 1972, 20(7): 266-267. doi: 10.1063/1.1654142 [4] Churin E G, Hobfeld J, Tschudi T. Polarization configuration with singular point formed by computer generated holograms [J]. Optics Communications, 1993, 99(1): 13-17. [5] Tidwell S C, Kim G H, Kimura W D. Efficient radially polarized laser beam generation with a double interferometer [J]. Applied Optics, 1993, 32(27): 5222-5229. doi: 10.1364/AO.32.005222 [6] Stalder M, Schadt M. Linearly polarized light with axial symmetry generated by liquid-crystal polarization converters [J]. Optics Letters, 1996, 21(23): 1948-1950. doi: 10.1364/OL.21.001948 [7] Youngworth K S, Brown T G. Focusing of high numerical aperture cylindrical-vector beams [J]. Optics Express, 2000, 7(2): 77-87. doi: 10.1364/OE.7.000077 [8] Dorn R, Quabis S, Leuchs G. Sharper focus for a radially polarized light beam [J]. Physical Review Letters, 2003, 91(23): 233901. doi: 10.1103/PhysRevLett.91.233901 [9] Zhan Q, Leger J. Focus shaping using cylindrical vector beams [J]. Optics Express, 2002, 10(7): 324-331. doi: 10.1364/OE.10.000324 [10] Kozawa Y, Sato S. Optical trapping of micrometer-sized dielectric particles by cylindrical vector beams [J]. Optics Express, 2010, 18(10): 10828-10833. doi: 10.1364/OE.18.010828 [11] Meier M, Romano V, Feurer T. Material processing with pulsed radially and azimuthally polarized laser radiation [J]. Applied Physics A, 2007, 86(3): 329-334. doi: 10.1007/s00339-006-3784-9 [12] Zhan Q. Cylindrical vector beams: from mathematical concepts to applications [J]. Advances in Optics and Photonics, 2009, 1(1): 1-57. doi: 10.1364/AOP.1.000001 [13] Liu Z, Liu Y, Ke Y, et al. Geometric phase Doppler effect: when struct light meets rotating structured materials [J]. Optics Express, 2017, 25(10): 111564-11573. [14] Wang H, Shi L, Yuan G, et al. Subwavelength and super-resolution nondiffraction beam [J]. Applied Physics Letters, 2006, 89(17): 171102. doi: 10.1063/1.2364693 [15] Zhang X, Xia T, Cheng S, et al. Free-space information transfer using the elliptic vortex beam with fractional topological charge [J]. Optics Communications, 2019, 431(1): 238-244. [16] Vieira J, Mendoca J T. Nonlinear laser drivendonutwakefields for positron and electron acceleration [J]. Physical Review Letters, 2014, 112(21): 215001. doi: 10.1103/PhysRevLett.112.215001 [17] Wang X, Li Y, Chen J, et al. A new type of vector fields with hybrid states of polarization [J]. Optics Express, 2010, 18(10): 10786-10795. doi: 10.1364/OE.18.010786 [18] Beckley A M, Brown T G, Alonso M A. Full Poincaré beams [J]. Optics Express, 2010, 18(10): 10777-10785. doi: 10.1364/OE.18.010777 [19] Yi X, Liu Y, Ling X, et al. Hybrid-order Poincare sphere [J]. Physical Review A, 2015, 91(2): 023801. doi: 10.1103/PhysRevA.91.023801 [20] Arora G, Rajput R, Senthilkumaran P. Full Poincaré beam with all the Stokes vortices [J]. Optics Letters, 2019, 44(22): 5638-5641. doi: 10.1364/OL.44.005638 [21] Ruchi A G, Senthilkumaran P. Hybrid order Poincaré spheres for Stokes singularities [J]. Optics Letters, 2020, 45(18): 5136-5139. doi: 10.1364/OL.400946 [22] Liu Y, Liu Z, Zhou J, et al. Measurements of Pancharatnam–Berry phase in mode transformations on hybrid-order Poincaré sphere [J]. Optics Letters, 2017, 42(17): 3447-3450. doi: 10.1364/OL.42.003447 [23] Wang H, Rui G, Zhan Q. Dynamic propagation of optical vortices embedded in full Poincaré beams with rotationally polarization symmetry [J]. Optics Communications, 2015, 351(1): 15-25. [24] Lerman G M, Stern L, Levy U. Generation and tight focusing of hybridly polarized vector beams [J]. Optics Express, 2010, 18(26): 27650-27657. doi: 10.1364/OE.18.027650 [25] Zhang L, Lin F, Qiu X, et al. Full vectorial feature of second-harmonic generation with full Poincaré beams [J]. Chinese Optics Letters, 2019, 17(9): 091901. [26] Zhang L, Qiu X, Li F, et al. Second harmonic generation with full Poincaré beams [J]. Optics Express, 2018, 26(9): 11678-11684. doi: 10.1364/OE.26.011678 [27] Zhang L, Qiu X, Zeng L, et al. Multiple trapping using a focused hybrid vector beam [J]. Chinese Physics B, 2019, 28(9): 094202. doi: 10.1088/1674-1056/ab33ef [28] Wei C, Wu D, Liang C, et al. Experimental verification of significant reduction of turbulence-induced scintillation in a full Poincaré beam [J]. Optics Express, 2015, 23(19): 24331-24341. doi: 10.1364/OE.23.024331 [29] Cardano F, Karimi E, Marrucci L, et al. Generation and dynamics of optical beams with polarization singularities [J]. Optics Express, 2013, 21(7): 8815-8820. doi: 10.1364/OE.21.008815 [30] Shvedov V, Karpinski P, Sheng Y, et al. Visualizing polarization singularities in Bessel Poincaré beams [J]. Optics Express, 2015, 23(9): 12444-12453. doi: 10.1364/OE.23.012444 [31] Garcia-Gracia H, Gutiérrez-Vega J C. Polarization singularities in nondiffracting Mathieu-Poincaré beams [J]. Journal of Optics, 2016, 18(1): 014006. doi: 10.1088/2040-8978/18/1/014006 [32] Nye G F. Polarization effects in the diffraction of electromagnetic waves: the role of disclinations [J]. Proceedings of the Royal Society of London Series A, 1983, 387(1792): 105-132. [33] Dennis M R. Polarization singularities in paraxial vector fields: morphology and statistics [J]. Optics Communications, 2002, 213(4-6): 201-221. doi: 10.1016/S0030-4018(02)02088-6 [34] Lopez-Mago D. On the overall polarisation properties of Poincaré beams [J]. Journal of Optics, 2019, 21(11): 115605. doi: 10.1088/2040-8986/ab4c25 [35] Fu S, Zhai Y, Wang T, et al. Tailoring arbitrary hybrid Poincaré beams through a single hologram [J]. Applied Physics Letters, 2017, 111(21): 211101. doi: 10.1063/1.5008954 [36] Han L, Qi S, Liu S, et al. Hybrid vector beams with non-uniform orbital angular momentum density induced by designed azimuthal polarization gradient [J]. Chinese Physics B, 2020, 29(9): 094203. doi: 10.1088/1674-1056/aba09d [37] Galvez E, Khadka S, Schubert W H, et al. Poincaré-beam patterns produced by nonseparable superpositions of Laguerre-Gauss and polarization modes of light [J]. Applied Optics, 2012, 51(15): 2925-2934. doi: 10.1364/AO.51.002925 [38] Lu T, Huang T, Wang J, et al. Generation of flower high-order Poincaré sphere laser beams from a spatial light modulator [J]. Scientific Reports, 2016, 6(1): 39657. doi: 10.1038/srep39657 [39] Wang Y, Wang L, Xin Y. Generation of full Poincaré beams on arbitrary order Poincaré sphere [J]. Current Optics and Photonics, 2017, 1(6): 631-636. [40] Ling X, Yi X, Dai Z, et al. Characterization and manipulation of full Poincaré beams on the hybrid Poincaré sphere [J]. Journal of the Optical Society of America B, 2016, 33(11): 2172-2176. doi: 10.1364/JOSAB.33.002172 [41] Li D, Feng S, Nie S, et al. Generation of arbitrary perfect Poincaré beams [J]. Journal of Applied Physics, 2019, 125(7): 073105. doi: 10.1063/1.5079850 [42] Gu Z, Yin D, Gu F, et al. Generation of concentric perfect Poincaré beams [J]. Scientific Reports, 2019, 9(1): 15301. doi: 10.1038/s41598-019-50705-z [43] Beckley A M, Brown T G, Alonso M A. Full Poincaré beams II: partial polarization [J]. Optics Express, 2012, 20(9): 9357-9362. doi: 10.1364/OE.20.009357 [44] Marrucci L, Manzo C, Paparo D. Pancharatnam-Berry phase optical elements for wave front shaping in the visible domain: switchable helical mode generation [J]. Applied Physics Letters, 2006, 88(22): 221102. doi: 10.1063/1.2207993 [45] Liu Z X, Liu Y Y, Ke Y G, et al. Generation of arbitrary vector vortex beams on hybrid-order Poincaré sphere [J]. Photonics Research, 2017, 5(1): 15-21. doi: 10.1364/PRJ.5.000015 [46] Lou S, Zhou Y, Yuan Y, et al. Generation of arbitrary vector vortex beams on hybrid-order Poincaré sphere based on liquid crystal device [J]. Optics Express, 2019, 27(6): 8596-8604. doi: 10.1364/OE.27.008596 [47] Zhang Y, Chen P, Ge S, et al. Spin-controlled massive channels of hybrid-order Poincare sphere beams [J]. Applied Physics Letters, 2020, 117(8): 081101. doi: 10.1063/5.0020398 [48] Khajavi B, Galvez E J. Preparation of Poincaré beams with a same-path polarization/spatial-mode interferometer [J]. Optical Engineering, 2015, 54(11): 111305. doi: 10.1117/1.OE.54.11.111305 [49] Alpmann C, Schlickriede C, Otte E, et al. Dynamic modulation of Poincaré beams [J]. Scientific Reports, 2017, 7(1): 8076. doi: 10.1038/s41598-017-07437-9 [50] Otte E, Alpmann C, Denz C. Polarization singularity explosions in tailored light fields [J]. Laser Photonics Reviews, 2018, 12(6): 1700200. doi: 10.1002/lpor.201700200 [51] Lerman G M, Levy U. Generation of a radially polarized light beam using space-variant subwavelength gratings at 1064 nm [J]. Optics Letters, 2008, 33(23): 2782-2784. doi: 10.1364/OL.33.002782 [52] Wang R, He S, Chen S, et al. Electrically driven generation of arbitrary vector vortex beams on the hybrid-order Poincaré sphere [J]. Optics Letters, 2018, 43(15): 3570-3573. doi: 10.1364/OL.43.003570 [53] Lin W B, Ota Y, Arakawa Y, et al. Microcavity-based generation of full Poincaré beams with arbitrary skyrmion numbers [J]. Physical Review Research, 2021, 3(2): 023055. doi: 10.1103/PhysRevResearch.3.023055 [54] Liu M Z, Huo P C, Zhu W Q, et al. Broadband generation of perfect Poincaré beams via dielectric spin-multiplexed metasurface [J]. Nature Communications, 2021, 12: 2230. doi: 10.1038/s41467-021-22462-z [55] Wang H, Shi L, Lukyanchuk B, et al. Creation of a needle of longitudinally polarized light in vacuum using binary optics [J]. Nature Photonics, 2008, 2(8): 501-505. doi: 10.1038/nphoton.2008.127 [56] Zang X, Bautista G, Turquet L, et al. Efficient hybrid-mode excitation in plasmonic nanoantennas by tightly focused higher-order vector beams [J]. Journal of the Optical Society of America B, 2021, 38(2): 521-529. doi: 10.1364/JOSAB.412195 [57] Zhu W, Shvedov V, She W, et al. Transverse spin angular momentum of tightly focused full Poincaré beams [J]. Optics Express, 2015, 23(26): 34029-34041. doi: 10.1364/OE.23.034029 [58] Man Z, Dou X, Urbach H P. The evolutions of spin density and energy flux of strongly focused standard full Poincaré beams [J]. Optics Communications, 2002, 458(1): 124790. [59] Man Z, Bai Z, Li J, et al. Focus shaping by tailoring arbitrary hybrid polarization states that have a combination of orthogonal linear polarization bases [J]. Applied Optics, 2018, 57(12): 3047-3055. doi: 10.1364/AO.57.003047 [60] Han W, Cheng W, Zhan Q W. Flattop focusing with full Poincaré beams under low numerical aperture illumination [J]. Optics Letters, 2011, 36(9): 1605-1607. doi: 10.1364/OL.36.001605 [61] Dai X, Li Y, Liu L. Tight focusing properties of hybrid-order Poincaré sphere beams [J]. Optics Communications, 2018, 426(1): 46-53. [62] Wang L G. Optical forces on submicron particles induced by full Poincaré beams [J]. Optics Express, 2012, 20(19): 20814-20826. doi: 10.1364/OE.20.020814 [63] Xue Y, Wang Y, Zhou S, et al. Focus shaping and optical manipulation using highly focused second-order full Poincaré beam [J]. Journal of the Optical Society of America A, 2018, 35(6): 953-958. doi: 10.1364/JOSAA.35.000953 [64] Sanchez M M, Davis J A, Moreno I, et al. Gouy phase effects on propagation of pure and hybrid vector beams [J]. Optics Express, 2019, 27(3): 2374-2386. doi: 10.1364/OE.27.002374 [65] Lu X, Wu Z, Zhang W, et al. Polarization singularities and orbital angular momentum sidebands from rotational symmetry broken by the Pockels effect [J]. Scientific Reports, 2014, 4(1): 4865. [66] Yang C, Zhou Z, Li Y, et al. Nonlinear frequency conversion and manipulation of vector beams in a Sagnac loop [J]. Optics Letters, 2019, 44(2): 219-222. doi: 10.1364/OL.44.000219 [67] Wu H, Zhou Z, Gao W, et al. Dynamic tomography of the spin-orbit coupling in nonlinear optics [J]. Physical Review A, 2019, 99(2): 023830. doi: 10.1103/PhysRevA.99.023830 [68] Wu H, Zhao B, Rosles-Guzmán, et al. Spatial-polarization-independent parametric up-conversion of vectorially structured light [J]. Physical Review Applied, 2020, 13(6): 064041. doi: 10.1103/PhysRevApplied.13.064041 [69] Silva N R, Oliveira A G, Arruda M F Z, et al. Stimulated parametric down-conversion with vector vortex beams [J]. Physical Review Applied, 2021, 15(2): 024039. doi: 10.1103/PhysRevApplied.15.024039 [70] Wen B, Rui G, He J, et al. Polarization rotation and singularity evolution of fundamental Poincaré beams through anisotropic Kerr nonlinearities [J]. Journal of Optics, 2020, 22(8): 08550. [71] Yang X, Chen Y, Wang J, et al. Observing quantum coherence induced transparency of hybrid vector beams in atomic vapor [J]. Optics Letters, 2019, 44(11): 2911-2914. doi: 10.1364/OL.44.002911 [72] Luo D, Hu H, Pan C, et al. Nonlinear control of polarization rotation of hybrid-order vector vortex beams [J]. Journal of Optics, 2020, 22(11): 115612. doi: 10.1088/2040-8986/abbecb -









 下载:
下载: