下载:
-
光学频率梳[1]（简称光频梳）是一种具有梳状离散的、等间隔的频率成分构成的相干光源。光频梳在频域上具有THz量级带宽，并兼具MHz量级频率精度，提供了连接光频段与微波段的有效途径[2]。凭借超高精度的频率标准，光频梳已被广泛应用于精密光谱、激光雷达、时间基准和地外行星探寻等众多领域，在科学研究、产业应用和国防军事上都具有重要意义。传统的光频梳主要基于锁模激光器产生，由于体积较大、功耗高、价格昂贵，并且对工作环境敏感[3-4]，大大限制了光频梳的应用。
近年来，通过克尔非线性效应产生的新型微腔光频梳[5-6]受到了广泛关注。对比锁模激光器的光频梳，首先，微腔光频梳在体积和功耗上有着极大的优势，有望实现单片集成的光频梳光源[7]；其次，微腔具有独特的回音壁模式[8]，具有极高的品质因子（Q值），显著增强了场效应，极大地降低了光频梳的工作阈值；最后，随着微加工技术逐渐成熟，微腔光频梳频率间隔可以轻松覆盖从GHz~THz区间范围[6]。2004年，T. Kippenberg等利用二氧化硅微芯圆环腔实现了四波混频效应[9]。2007年，P. Del’Haye等通过将连续光泵浦石英微芯圆环腔，首次实现了微腔光频梳[10]并观察到了超过500 nm宽光频梳输出，验证了微腔光频梳的可行性。但是，产生微腔光频梳通常处于调制不稳定状态，相干性不高、稳定性不好，时域波形无法形成稳定的锁模超短脉冲。2014年，Herr等在氟化镁(MgF2)晶体材料微腔中观察到了大带宽、高相干性、强稳定性孤子光频梳[11]，完美解决了这一问题。MgF2晶体对周围环境湿度不敏感，相比二氧化硅材料具有非线性系数大、吸收常数小、缺陷少和纯度高的优势，是产生克尔光频梳的理想材料。另外，MgF2透明波段较宽，从紫外波段覆盖至中红外波段，2015年，OEwaves公司的研究人员采用量子级联激光器作为泵浦源，在MgF2微腔中产生了中心波长位于4.5 μm的光频梳，是目前已知波长最长的中红外微腔光频梳[12]。2019年，Shun F等通过调控MgF2晶体微腔色散，满足了四波混频分立的相位匹配条件，得到频移量高达140 THz的边带[13]。至今，MgF2微腔光频梳已在中红外光谱[12]、太赫兹信号产生[13]、超低相位噪声微波信号[14]、空间复用[15]等应用中显现重要价值。
文中首先通过超精密加工的方法制备了氟化镁晶体微腔，采用光纤锥波导的方式实现了高效耦合。得到的谐振模式不仅具有高Q值，且频谱干净，为产生克尔光频梳提供了有力保证。其次，在实验结果的基础上结合Lugiato-Lefever方程，推演了氟化镁微腔中产生过程，分析了泵浦功率、失谐量对光频梳的影响。最后，通过调控几何色散来改变构成的微腔色散得到了多孤子态的光频梳，实现了光频梳的光谱范围拓宽，为产生具有光滑包络的孤子光频梳奠定了基础。
-
开发了超精密加工装置制备氟化镁微腔。首先，将氟化镁晶体样品固定在主轴上，主轴带动晶体高速旋转，通过精密抛光工艺得到具有超光滑表面的氟化镁微腔。然后，在得到回转椭球体墙体的基础上再通过刀具切削成V型。由于腔体侧壁的形状对微腔谐振特性具有决定性作用，则需要在侧壁及其对称性方向的有效厚度尽量薄。因此，文中制备了具有V型结构的氟化镁微盘腔，直径约为7 mm，实物图如图1(a)所示。通过白光干涉仪表征了腔体侧壁的形状，如图1(b)所示，轮廓基本呈现V型，并且表面非常洁净。
图 1 (a) MgF2晶体腔实物图；(b)腔体侧壁轮廓表征结果
Figure 1. (a) Picture of MgF2 crystalline resonator; (b) Characterization results of cavity sidewall profile
-
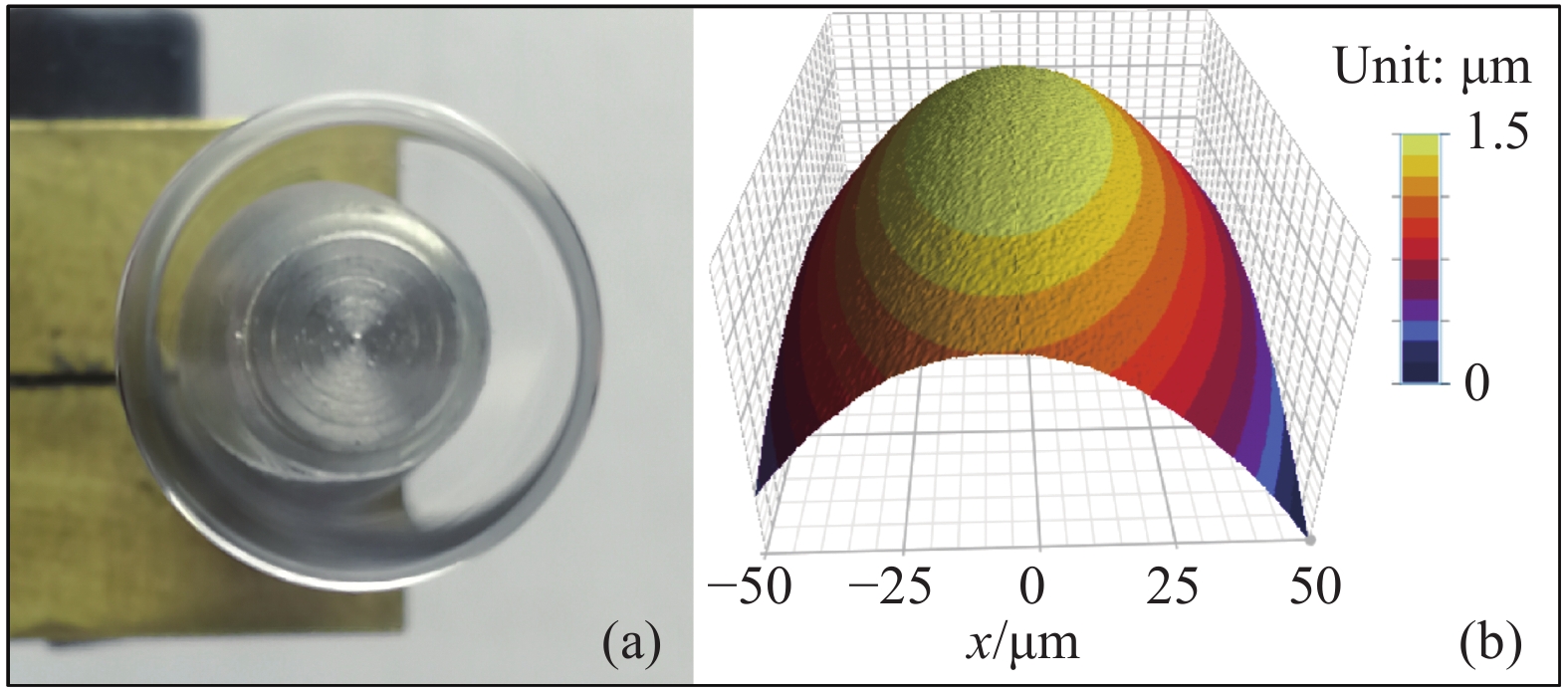
氟化镁晶体微腔在毫米量级，激发的回音壁谐振模式过多，不易分辨，V型结构的两条楔边可以显著抑制极性角方向的模式，且V型结构角度越小，抑制能力越强。不同于规则的球形或柱形微腔[16]，直接求解V型结构微腔的解析解是非常困难的。图2为使用有限元软件COMSOL对V型结构微盘腔的模式场分布的结果，每个模式用(n，l，m) 3个量子数来表示，其中，n为径向模式数，描述了光场的径向分布在腔内的波节数；l为角向模式数，描述了光场在赤道面的波节数；m为方位角模式数，描述了光场在子午面的波节数。n=1、l=m的模式为基模，具有最小的模式体积。n越大其模式的电场分布越靠腔内，模式体积越大；l-m越大，则模式分布越趋向两极，模式体积越大且能量分布越分散。
图 2 MgF2微腔结构的模式电场分布
Figure 2. Mode electric field distribution of MgF2 microresonator structure
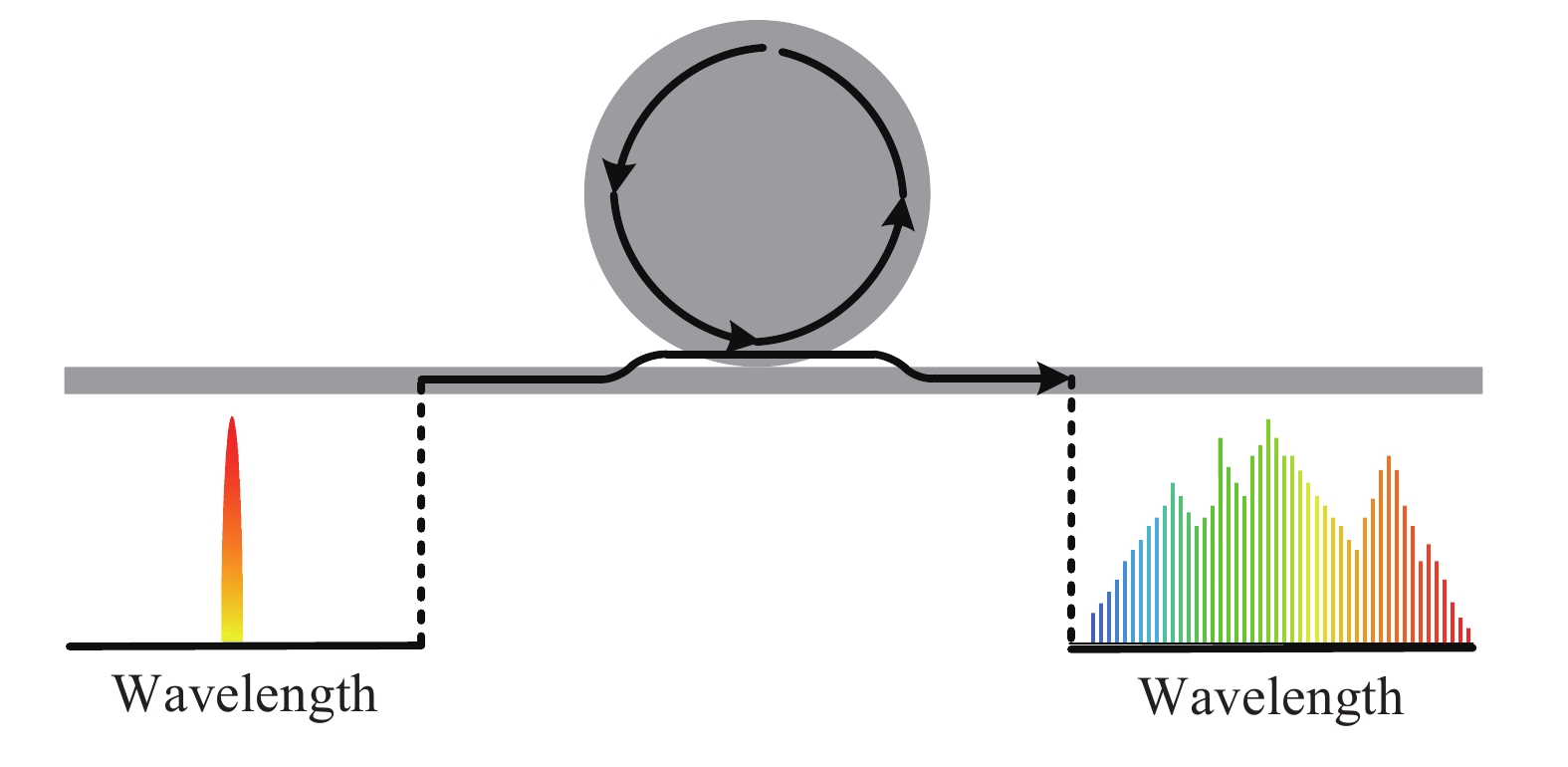
利用微腔克尔效应产生光频梳的结构如图3所示。微腔光频梳产生依赖于非线性参量过程[5]，当泵浦激光耦合进入克尔微腔，腔内先通过简并 FWM 产生较优邻近模式的频率成分，新频率成分进而与泵浦频率成分发生非简并FWM以拓宽光谱。由于高Q值微腔极强的场增强因子和天然的滤波结构，新的频率成分获得参量增益并形成参量振荡，产生一系列等间隔的光谱梳齿线，即克尔微腔光频梳。
图 3 基于微腔结构的光频梳示意图
Figure 3. Schematic of optical frequency comb based on microresonator structure
外部光场通过波导耦合进微腔的动力学模型可以通过Lugiato-Lefever方程[17] (LLE)描述：
$$ \begin{split} {\tau _r}\dfrac{{\partial \psi }}{{\partial t}} =& ({\alpha _i}L/2 + {T_c}/2 + i{\delta _0})A(t,T)+ i\displaystyle\sum\limits_{k \geqslant 2} {\frac{{{i^k}L}}{{{\beta _k}}}} \frac{{\partial A(\tau ,T)}}{{\partial {T^k}}} +\\ &i\gamma L{\left| {A(\tau ,T)} \right|^2}A(\tau ,T)+\sqrt {{T_c}} {A_{in}}\\[-10pt] \end{split} $$ (1) 式中：A(τ, T)描述慢变光场下的复振幅；τr对应光场沿微腔传输一周的时间，与自由光谱范围FSR呈倒数关系既有τr=1/FSR；αi表示线性损耗系数；δ0表示了泵浦激光与谐振频率间失谐系数；L表示微腔的腔长；Tc描述了泵浦光与微腔的功率耦合系数；βk描述了微腔的k阶色散；γ为非线性系数；Ain表示泵浦光的振幅。公式(1)对于腔内光场的演化有一定局限性，其在数值仿真中需要实际的微腔参数作为依据，不具有普遍性，因此对公式(1)进行归一化处理，在仅仅考虑二阶色散的情况下，归一化LLE方程式为：
$$\dfrac{{\partial \psi }}{{\partial t}} = \left[ { - (1 + i\delta ) - i\beta \dfrac{\partial }{{\partial {t^2}}} + i{{\left| \varPsi \right|}^2}} \right]\varPsi + f{}_0$$ (2) 式中：δ表示归一化失谐系数δ=δ0/α；β为归一化色散系数β=β2(2π/τr)2/2α；f0表示归一化泵浦光功率
${f_0} = $ $ \sqrt {\gamma L{T_c}/{\alpha ^3}} {A_{in}}$ ；α表示损耗系数；β2为群色散速度。归一化LLE方程中光场围绕腔体一周的时间τr变为了2π。能够看出，微腔内光场的演变过程主要受制于色散系数β、失谐系数δ、以及耦合进入微腔的泵浦光功率f0。此外，损耗系数α与Q值息息相关，Q值愈大，激发光频梳所需的激光振幅的阈值愈小。 -
微腔中的模式是被束缚在腔体内部的，需用波导器件通过倏逝场与微腔进行耦合。图4(a)为采用锥腰直径为3 μm的锥形光纤波导耦合MgF2微腔在1 550 nm波长附近得到的透射谱。由图可以看出，稳定激发出的模式频谱只有3~4个谐振模式，表现的非常干净，相比之前制备的回转椭球体微腔[18]的模式频谱更加干净规律，并且排列规则，为产生光滑包络的孤子光频梳提供良好的模式谱条件。
图 4 (a) MgF2微腔透射谱; (b) 洛伦兹拟合谱线
Figure 4. (a) Transmission spectrum of MgF2 microresonator; (b) Lorentz fitted spectral line
通过透射谱计算得到FSR为9.73 GHz，与理论结果相比较：FSR=c/(πD·n1)，代入光速c=3×108 m/s，直径D=7 mm，折射率n1=1.37，得到理论值FSR=9.8 GHz基本一致。另外，ΔFSR为0.37 GHz。实验谱线符合Lorentz线型描述，选取典型谐振模式(38.4 MHz处)进行拟合，其结果如图2(b)所示，计算得到该谐振腔的Q值达到了4.8×107。相比采用化学机械抛光法制备的V型氟化物微腔的模式频谱[19]得到的Q值要高一个数量级。如此高Q值的微腔，可大大降低产生光频梳的泵浦功率阈值，仅需很低的阈值便可激发微腔内的克尔效应。
得到频谱特性后，对MgF2微腔系统的光频梳产生过程进行研究。对于特定几何形状构成的腔体，材料一旦确立，在泵浦光波长扫描下，其二阶色散的变化范围非常窄可认为其基本保持不变。理论分析得到氟化镁群色散速度为β2=−0.925×10−26 s2/m，在仅考虑二阶色散的情况下，结合LLE方程以及谐振腔参数进行归一化处理。设定泵浦激光脉冲服从高斯分布，ψ0=2exp[(−1)×(t/0.3)2]，MgF2微腔有效参数归一化频率失谐系数δ=0.1，归一化色散系数β=−0.002 3，归一化泵浦功率量f02=0.1，结合Q值与损耗系数α的关系，因此，应用归一化低阈值泵浦光振幅Ain即可得到对应激发频谱。
图5(a)泵浦功率值f02=2.0较低，光频梳特征表现为单个主梳，此时耦合进微腔的光能量并不能激发光频梳。在图5(b)随着泵浦功率增大至f02=2.1耦合进微腔的能量提高，激发光频梳的泵浦功率达到一定的阈值光梳由单梳逐步变为多梳，并且以等间隔FSR出现主梳。图5(c)、(d)，在激发光频梳后，继续增大泵浦功率至f02=3.0及5.0时，腔体内束缚的能量越大其边带转换效率越大，边带效应持续加强，能够产生更多的谱线，主梳旁边次梳不断拓展，此时在时域主要表现为稳定波形。如图5(e)、(f)所示，随着功率持续加大f02=8.0和11.0，主梳之间次梳继续增加，变得杂乱无章。腔内原本稳定的图灵环状态逐渐被破坏，在剧烈的非线性效应逐渐失去了稳定性，此时在该状态下被称之为混沌态[20]。
图 5 (a)~(f) 恒定失谐下泵浦功率变化下光频梳演化过程
Figure 5. (a)-(f) Evolution process of optical frequency comb under constant detuning with varying pump power
为进一步研究频率失谐系数对光频梳演化过程的影响，在保持色散量，光脉冲形式等有效参数不变，泵浦功率系数f02=3.0，改变归一化频率失谐量观察对光频梳特性的影响。图6(a)中，在初始归一化失谐系数δ=0.0状态下，此时激发出光频梳，并且谱线周围出现零散的对称谱线，该阶段中频域主要表现为多倍的FSR的初始谱线构成，在时域中则表现为稳定的规则的图灵环曲线，此阶段也称之为稳定的调制不稳定阶段(SMI)。继续改变失谐系数（δ=1.5，见图6(b)），上一个稳定的阶段被打破，此时主梳之间具有了强烈的边带效应并且激发出有规律并且逐渐变得密集起来的次梳，时域中稳定的图灵环开始变得不稳定。继续改变失谐系数时(δ=2.0，见图6(c)），打破了上一个不稳定阶段，光梳变得杂乱无章，时域中出现不稳定的杂波，对应于不稳定的调制不稳定阶段(UMI) [20]。当失谐系数继续增大(δ=2.6，见图6(d))，边带能效再次加大出现，光梳经过上一个不稳定的阶段进入孤子状态即稳定的腔孤子状态(SCM)。与SMI态光频梳相比，孤子态光频梳有着更好的相干性和稳定性，更具有应用价值。
图 6 (a)~(d) 恒定功率下失谐变化光频梳演化过程
Figure 6. (a)-(d) Evolution process of an optical frequency comb with detuning changes under constant power
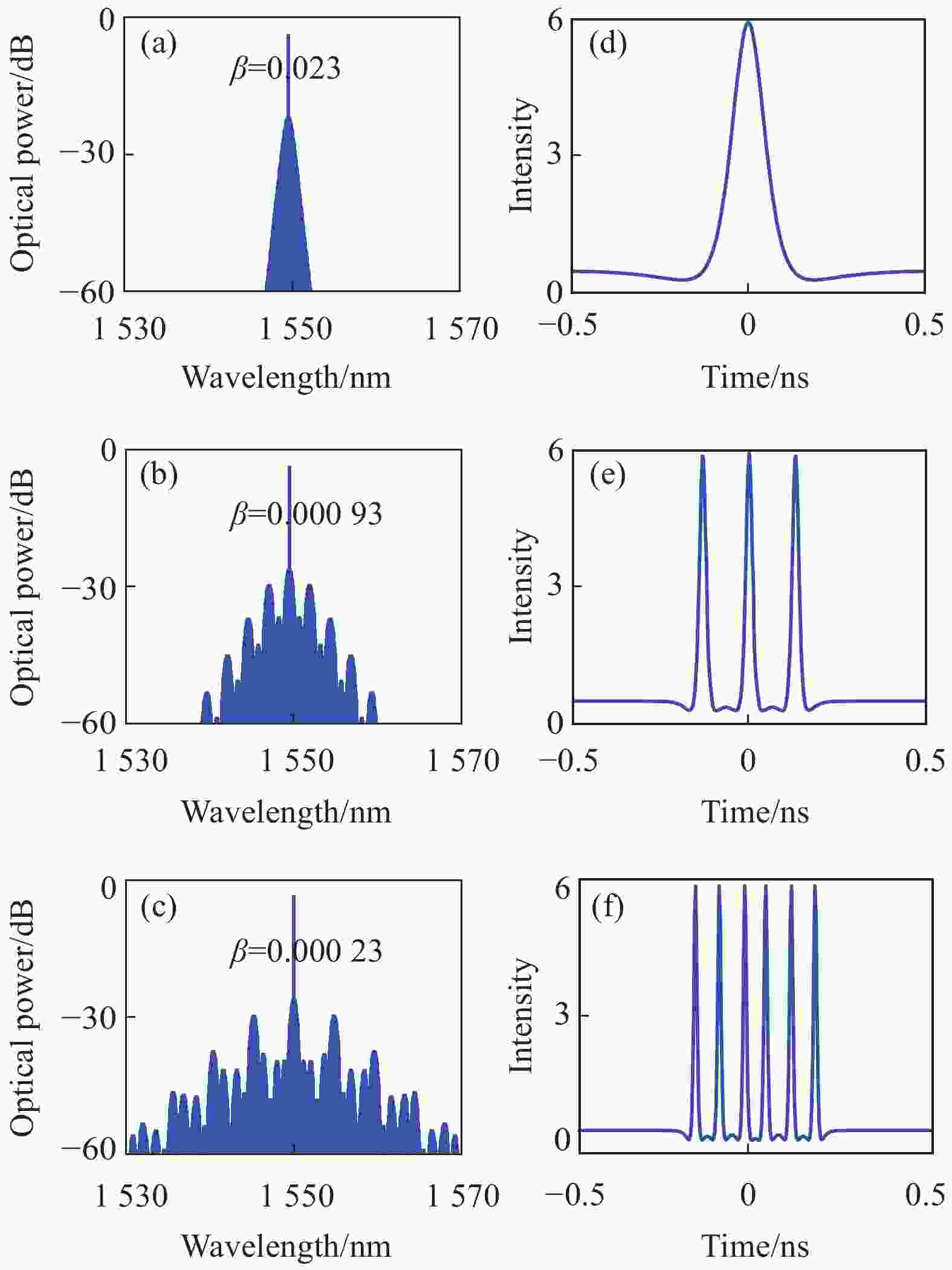
最后研究了色散变化对光频梳演化过程的影响。色散包含材料色散和几何色散，材料色散由材料本身决定，而在不同的结构下几何色散性质不同，可以通过改变V型结构角度的大小调控微腔的几何色散，达到调控总的色散的目的。图7(a)~(c)展示了通过调控几何色散情况下，孤子态光频梳频谱的演变过程。当失谐系数δ=2.6、泵浦功率f02=2.6不变时，当归一化色散逐渐减小(β分别为0.023、0.000 93、0.000 23)时，可以看出，光频梳的频谱展宽范围从8 nm增加到40 nm，大大增加了光频梳频谱的波段，证明了在优化色散的过程中达到了提升微腔光频梳性能的目的。此外，通过对应的时域谱图，如图7(d)~(e)所示，观察到光频梳孤子态的变化。可以看出，图7(a)~(c)分别对应单孤子、三孤子和六孤子，逐渐往多孤子态转移，在实际实验中还需考虑拉曼效应[21]、热效应[22]等因素对频谱的影响。
图 7 (a)~(c) 色散变化对光频梳演化过程的影响；(d)~(f) 对应不同孤子态的时域谱图
Figure 7. (a)-(c) Influence of dispersion variation on the evolution of optical frequency comb; (d)-(f) Time-domain spectra of different soliton states
-
文中分析了MgF2微腔克尔光频梳产生过程，通过超精密加工方法制备了Q值达到4.8×107的MgF2微腔，并且得到了干净规律、排列规则的频谱，为产生低重复频率光频梳提供了条件。结合归一化LLE方程研究了泵浦功率、失谐系数、色散变化对光频梳的影响，当泵浦功率达到光频梳的泵浦功率后，随着光功率的增加，光频梳在调制不稳定状态中逐步进入图灵环进而演化到混沌态。在特定光功率下，通过改变失谐系数，光频梳由调制不稳定状态进入孤子状态。通过改变色散拓展了微腔光频梳频谱，提升了光频梳性能，为氟化镁微腔光频梳的应用提供了可靠的理论基础。
Research on Kerr optical frequency comb generation based on MgF2 crystalline microresonator with ultra-high-Q factor
-
摘要: 克尔光频梳具有等距分布的梳状光谱结构，在精密测量、光钟、相干光通信、微波和光学任意波产生、光谱学及天文光谱仪校准等方面有着重要的应用。首先，微腔光频梳与其他光频梳系统相比，具有集成性高、体积小、功耗低的优势，大大扩展了光频梳的应用；其次，通过超精密加工方法制备了品质因子Q值达到了4.8×107的氟化镁微腔，并且得到了干净规律、排列规则的谐振谱，自由频率范围为9.73 GHz，为产生低重复频率光频梳提供了条件；最后，根据实验结果结合Lugiato-Lefever方程分析了氟化镁微腔光频梳的产生过程，研究了泵浦功率对光频梳的影响，通过调整失谐参数得到了孤子态光频梳。并且通过色散调控优化了微腔的光场模式，为产生具有超光滑光谱的孤子光频梳创造了先决条件，提升了光频梳性能。Abstract: Kerr optical frequency comb has an equidistantly distributed comb-like spectral structure and has important applications in precision measurement, optical clocks, coherent optical communications, microwave and optical arbitrary wave generation, spectroscopy, and calibration of astronomical spectrometers. Firstly, compared with other optical frequency comb systems, the microresonator optical frequency comb has the advantages of strong integration, small size and good flexibility, which greatly expands the application of optical frequency combs. Secondly, a MgF2 microresonator with a quality factor up to 4.8×107 was prepared by an ultra-precision machining method, and a clean, regular and regularly arranged spectrum was obtained. The free frequency range was 9.73 GHz, which provides conditions for generating low repetition rate optical frequency combs. Finally, according to the experimental results and the Lugiato-Lefever equation, the generation process of the MgF2 microresonator optical frequency comb was analyzed, and the influence of the pump power on the optical frequency comb was studied. The soliton state optical frequency comb was obtained by adjusting the detuning parameters. In addition, the optical field mode of the microresonator was optimized through dispersion control, which creates a condition for generating a soliton optical frequency comb with an ultra-smooth spectrum and improves the performance of the optical frequency comb.
-
Key words:
- optical microresonator /
- MgF2 /
- quality factor /
- optical frequency comb /
- soliton
-
图 1 (a) MgF2晶体腔实物图；(b)腔体侧壁轮廓表征结果
Figure 1. (a) Picture of MgF2 crystalline resonator; (b) Characterization results of cavity sidewall profile
图 2 MgF2微腔结构的模式电场分布
Figure 2. Mode electric field distribution of MgF2 microresonator structure
图 3 基于微腔结构的光频梳示意图
Figure 3. Schematic of optical frequency comb based on microresonator structure
图 4 (a) MgF2微腔透射谱; (b) 洛伦兹拟合谱线
Figure 4. (a) Transmission spectrum of MgF2 microresonator; (b) Lorentz fitted spectral line
图 5 (a)~(f) 恒定失谐下泵浦功率变化下光频梳演化过程
Figure 5. (a)-(f) Evolution process of optical frequency comb under constant detuning with varying pump power
图 6 (a)~(d) 恒定功率下失谐变化光频梳演化过程
Figure 6. (a)-(d) Evolution process of an optical frequency comb with detuning changes under constant power
-
[1] Teets R, Eckstein J, Hänsch T W. Coherent two-photon excitation by multiple light pulses [J]. Physical Review Letters, 1977, 38(14): 760-764. doi: 10.1103/PhysRevLett.38.760 [2] Diddams S A. The evolving optical frequency comb [J]. Journal of the Optical Society of America B, 2010, 27(11): B51-B62. doi: 10.1364/JOSAB.27.000B51 [3] Spence D E, Kean P N, Sibbett W. 60-fsec pulse generation from a self-mode-locked Ti sapphire laser [J]. Optics Letters, 1991, 16(1): 42-44. doi: 10.1364/OL.16.000042 [4] Tamura K, Ippen E P, Haus H A, et al. 77-fs pulse generationfrom astretched-pulse mode-locked all-fiber ring laser [J]. Optics Letters, 1993, 18(13): 1080-1082. doi: 10.1364/OL.18.001080 [5] Kippenberg T J, Holzwarth R, Diddams S A. Microresonator-based optical frequency combs [J]. Science, 2011, 332(6029): 555-559. doi: 10.1126/science.1193968 [6] Kippenberg T J, Gaeta A L, Lipson M, et al. Dissipative Kerr solitons in optical microresonators [J]. Science, 2018, 361(6402): 8083. doi: 10.1126/science.aan8083 [7] Shen B, Chang L, Liu J, et al. Integrated turnkey soliton microcombs [J]. Nature, 2020, 582(18): 365-369. [8] Vahala K J. Optical microcavities [J]. Nature, 2003, 424(6950): 839-646. doi: 10.1038/nature01939 [9] Kippenberg T J, Spillane S M, Vahala K J. Kerr-nonlinearity optical parametric oscillation in an ultrahigh-Q toroid microcavity [J]. Physical Review Letters, 2004, 93(8): 083904. doi: 10.1103/PhysRevLett.93.083904 [10] Del'Haye P, Schliesser A, Arcizet O, et al. Optical frequency comb generation from a monolithic microresonator [J]. Nature, 2007, 450(7173): 1214-1217. doi: 10.1038/nature06401 [11] Herr T, Brasch V, Jost J D, et al. Temporal solitons in optical microresonators [J]. Nature Photonics, 2014, 8: 145-152. doi: 10.1038/nphoton.2013.343 [12] Savchenkov A A, Ilchenko V S, Teodoro F D, et al. Generation of Kerr combs centered at 4.5 μm in crystalline microresonators pumped with quantum-cascade lasers [J]. Optics Letters, 2015, 40: 3468-3471. doi: 10.1364/OL.40.003468 [13] Fujii S, Tanaka S, Fuchida M, et al. Octave-wide phase-matched four-wave mixing in dispersion engineered crystalline microresonators [J]. Optics Letters, 2019, 44: 3146-3149. doi: 10.1364/OL.44.003146 [14] Lucas E, Brochard P, Bouchand R, et al. Ultralow-noise photonic microwave synthesis using a soliton microcomb-based transfer oscillator [J]. Nature Communications, 2020, 11: 374. doi: 10.1038/s41467-019-14059-4 [15] Lucas E, Lihachev G, Bouchand R, et al. Spatial multiplexing of soliton microcombs [J]. Nature Photonics, 2018, 12: 699-705. doi: 10.1038/s41566-018-0256-7 [16] Chiasera A, Dumeige Y, Féron P, et al. Spherical whispering-gallery mode microresonators [J]. Laser & Photonics Review, 2010, 4(3): 457-482. [17] Coen S, Randle H G, Sylvestre T, et al. Modeling of octave-spanning Kerr frequency combs using a generalized mean-field Lugiato–Lefever model [J]. Optics Letters, 2013, 38(1): 37-39. doi: 10.1364/OL.38.000037 [18] Wang Mengyu, Yang Yu, Wu Tao, et al. Fabrication and resonance characteristic analysis of spheroid Calcium Fluoride millimeter crystalline microcavity [J]. Acta Optica Sinica, 2021, 41(8): 0823019. (in Chinese) doi: 10.3788/AOS202141.0823019 [19] Lu X, Xue C, Wang Y, et al. Fabrication and test of millimeter-size CaF2 disk resonator [J]. Infrared and Laser Engineering, 2015, 44(10): 3049-3054. (in Chinese) doi: 10.3969/j.issn.1007-2276.2015.10.031 [20] Herr T, Hartinger K, Riemensberger, et al. Universal formation dynamics and noise of Kerr-frequency combs in microresonators [J]. Nature Photonics, 2012, 6: 480-487. doi: 10.1038/nphoton.2012.127 [21] Yoshitomo O, Yu M, Vivek V. Competition between Raman and Kerr effects in microresonator comb generation [J]. Optics Letters, 2017, 42(14): 2786-2789. doi: 10.1364/OL.42.002786 [22] Jiang X, Yang L. Opto-thermal dynamics in whispering-gallery microresonators [J]. Light: Science & Applications, 2020, 9: 24. -
点击查看大图
计量
- 文章访问数: 401
- HTML全文浏览量: 112
- PDF下载量: 83
- 被引次数: 0
