-
捷联惯导系统被广泛应用于导航领域,惯性测量单元(IMU)是惯导系统中的核心部件,激光陀螺和石英挠性加速度计是目前在IMU中广泛采用的惯性器件,由于惯性器件存在标度因数误差、零偏等器件误差,且IMU在装配过程中会引入安装角误差等,因此需要对误差参数进行精确标定,IMU的标定精度是影响捷联惯导系统定位精度的重要因素之一[1]。
传统的误差参数标定方法主要包括分立式标定和系统级标定。分立式标定利用高精度的转台,提供精确的方位、位置和角速率基准。通过参考当地重力加速度和地球自转角速率,将IMU放置在不同位置,可以将激光陀螺和加速度计的误差项标定出来[2-3]。但是分立式标定的标定精度从根本上受限于转台精度[4],而高精度的转台设备成本过大,这使得分立式标定的精度很难大幅提升。
系统级标定方法通过观测导航解算误差对IMU的各项误差参数进行估计,可以从根本上摆脱转台精度对标定结果的影响。目前对于系统级标定的研究主要集中在标定路径的编排和卡尔曼滤波器的设计两大方面。标定路径编排的首要目的是误差传递解耦和提高误差参数的可观测性。参考文献[5]设计了一种18位置的标定方案,可以在20 min内达到导航级惯性导航系统的标定精度要求,目前被广泛采用。参考文献[6]设计了一种25位置转动编排方式,额外考虑了加速度计的二次项误差和内杆臂的误差,并验证了标定路径的可行性。卡尔曼滤波器的设计主要基于IMU误差模型的建立和捷联惯导系统误差传播方程。参考文献[7]利用经纬度误差作为观测量,对激光陀螺的漂移进行精确辨识。刘冰[8]等设计了一种基于高阶卡尔曼滤波算法的系统级标定方法。石文峰[1]等设计了十位置系统级标定路径,并建立了33维的卡尔曼滤波器对误差参数进行估计。张红良[9]设计了一种系统级标定卡尔曼滤波方法,额外考虑了系统的内杆臂效应。于海龙[10]设计了一种33维的卡尔曼滤波器,考虑了加速度计二次项误差系数,并通过仿真实验加以验证。
在传统的激光陀螺和加速度计误差建模的基础上,由于机械结构及安装原因,3个加速度计敏感质心和IMU质心不重合,从而造成因加速度计测量点不同而引起的导航误差,这种误差效应被称为内杆臂效应。同时,在大多数工作条件下,IMU的标定参数被认为是固定值。但在温度变化范围较大时,由于石英挠性加速度计的输出对工作温度敏感[11-14],其标定参数随之变化,因此需要对加速度计的标定参数进行补偿,以消除温度变化引起的标定参数热漂移误差。目前广泛采用的温度补偿方法主要为求解标定参数的温度误差系数,从而构建标定参数的温度模型[13]。
基于此,文中重点研究系统级标定法卡尔曼滤波器的设计,额外考虑了加速度计的内杆臂效应和标定参数的温度误差系数等复杂误差源。设计了一种基于45维卡尔曼滤波器的系统级标定方法,并通过温度控制试验箱控制标定过程中的温度变化。仿真及实验结果表明,该方法能够精确标定出激光陀螺和加速度计的零偏、标度因数误差、安装角误差以及加速度计的内杆臂参数和温度误差系数。导航实验结果证明,使用经过温度误差系数和内杆臂参数误差反馈后的标定参数进行导航解算,可以显著提升惯导系统导航精度。
-
文中定义的坐标系包括惯性参考系(i系)、地球参考系(e系)、导航坐标系(n系) (xyz轴分别指向北东地方向)以及IMU坐标系(b系) (xyz轴分别指向右前上方向)。
-
在IMU中,由于加速度计的安装质心与IMU的质心不重合,当载体存在角运动时,加速度计会敏感到额外的切向和向心加速度,此误差即为加速度计的内杆臂效应误差,其表达式为:
$$ \left\{ \begin{gathered} {\delta _{ax}} = \frac{{{\rm d}\omega _{ib}^b}}{{{\rm d}t}} \times {r_x} + \omega _{ib}^b \times \omega _{ib}^b \times {r_x} \\ {\delta _{ay}} = \frac{{{\rm d}\omega _{ib}^b}}{{{\rm d}t}} \times {r_y} + \omega _{ib}^b \times \omega _{ib}^b \times {r_y} \\ {\delta _{az}} = \frac{{{\rm d}\omega _{ib}^b}}{{{\rm d}t}} \times {r_{\textit{z}}} + \omega _{ib}^b \times \omega _{ib}^b \times {r_{\textit{z}}} \\ \end{gathered} \right. $$ (1) 式中:
${\delta _{ai}}(i = x,y,{\textit{z}})$ 为杆臂效应误差;$\omega _{ib}^b$ 为b系相对于i系的旋转角速度;${r_i}(i = x,y,{\textit{z}})$ 为载体质心到3个加速度计安装质心的矢量,即内杆臂参数[15]。在加速度计误差模型中,忽略角加速度的的影响,且加速度计的安装误差为小量,因此只考虑敏感轴方向上的杆臂效应。经过简化后的内杆臂误差方程为:$$ \left[ {\begin{array}{*{20}{c}} {{\delta _{ax}}} \\ {{\delta _{ay}}} \\ {{\delta _{a{\textit{z}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{({{\left[ {\omega _{ib}^b \times } \right]}^2})}_{11}}}&0&0 \\ 0&{{{({{\left[ {\omega _{ib}^b \times } \right]}^2})}_{22}}}&0 \\ 0&0&{{{({{\left[ {\omega _{ib}^b \times } \right]}^2})}_{33}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{r_x}} \\ {{r_y}} \\ {{r_{\textit{z}}}} \end{array}} \right] $$ (2) 对于中高精度的石英挠性加速度计而言,需要考虑由温度变化引起的标度因数误差、安装误差和零偏的热漂移误差。综上,加速度计的误差模型为:
$$ \begin{split}& \left[ {\begin{array}{*{20}{l}} {\delta f_x^b} \\ {\delta f_y^b} \\ {\delta f_{\textit{z}}^b} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{B_{ax}}} \\ {{B_{ay}}} \\ {{B_{a{\textit{z}}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{l}} {\Delta {T_{ax}} * T{B_{ax}}} \\ {\Delta {T_{ay}} * T{B_{ay}}} \\ {\Delta {T_{a{\textit{z}}}} * T{B_{a{\textit{z}}}}} \end{array}} \right]{\text{ + }}\left[ {\begin{array}{*{20}{l}} {{\delta _{ax}}} \\ {{\delta _{ay}}} \\ {{\delta _{a{\textit{z}}}}} \end{array}} \right] + \\& \left[ {\begin{array}{*{20}{l}} {\delta {K_{ax}}}&{\delta {M_{axy}}}&{\delta {M_{ax{\textit{z}}}}} \\ {\delta {M_{ayx}}}&{\delta {K_{ay}}}&{\delta {M_{ay{\textit{z}}}}} \\ {\delta {M_{a{\textit{z}}x}}}&{\delta {M_{a{\textit{z}}y}}}&{\delta {K_{a{\textit{z}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {f_x^b} \\ {f_y^b} \\ {f_{\textit{z}}^b} \end{array}} \right] + \\& \left[ {\begin{array}{*{20}{l}} {\Delta {T_{ax}} * T{K_{ax}}}&{\Delta {T_{ay}} * T{M_{axy}}}&{\Delta {T_{a{\textit{z}}}} * T{M_{ax{\textit{z}}}}} \\ {\Delta {T_{ax}} * T{M_{ayx}}}&{\Delta {T_{ay}} * T{K_{ay}}}&{\Delta {T_{a{\textit{z}}}} * T{M_{ay{\textit{z}}}}} \\ {\Delta {T_{ax}} * T{M_{a{\textit{z}}x}}}&{\Delta {T_{ay}} * T{M_{a{\textit{z}}y}}}&{\Delta {T_{a{\textit{z}}}} * T{K_{a{\textit{z}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {f_x^b} \\ {f_y^b} \\ {f_{\textit{z}}^b} \end{array}} \right] \\ \end{split} $$ (3) 式中:fib是在b系下沿i轴方向的不含误差因素的真实比力输出;δfb是比力的误差;Bai是i轴加速度计的零偏;TBai是加速度计零偏的一阶温度系数;δKai是i轴加速度计的标度因数误差;TKai是加速度计标度因数误差的一阶温度系数;δMaij(i=x,y,z, j=x,y,z, i≠j)是i轴加速度计与b系oij平面的安装误差角;TMaij是加速度计安装误差的一阶温度系数;∆Tai是i轴加速度计表面的温度变化率。
-
激光陀螺典型误差模型为:
$$ \left[ {\begin{array}{*{20}{c}} {\delta \omega _{ibx}^b} \\ {\delta \omega _{iby}^b} \\ {\delta \omega _{ib{\textit{z}}}^b} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{B_{gx}}} \\ {{B_{gy}}} \\ {{B_{g{\textit{z}}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\delta {K_{gx}}}&0&0 \\ {\delta {M_{gyx}}}&{\delta {K_{gy}}}&0 \\ {\delta {M_{g{\textit{z}}x}}}&{\delta {M_{g{\textit{z}}y}}}&{\delta {K_{g{\textit{z}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\omega _{ibx}^b} \\ {\omega _{iby}^b} \\ {\omega _{ib{\textit{z}}}^b} \end{array}} \right] $$ (4) 式中:
$\omega _{ibj}^b$ 为在b系下沿j轴方向的不含误差因素的真实角速率输出;$\delta \omega _{ib}^b$ 为角速率的误差;Bgi为i轴激光陀螺的零偏;δKgi为i轴激光陀螺的比例因子误差;δMgij(i=y,z,j=x,y,i≠j)为i轴激光陀螺与b系oij平面的安装误差角。 -
为了标定IMU误差模型中的所有误差参数,文中提出了一种基于45维卡尔曼滤波器的系统级标定方法。卡尔曼滤波器的主要功能是通过观测导航解算的速度和位置误差来估计IMU的误差参数。基于传统的捷联惯导系统误差传播方差[16],文中在考虑加速度计的内杆臂效应和温度误差系数的前提下对速度误差方程进行了扩展。
$$\begin{split}& {\dot \phi = \phi \times \omega _{in}^n + \delta \omega _{in}^n - C_b^n([\delta {K_g}] + [\delta {M_g}])\omega _{ib}^b - B_g^n}\\& {\delta {{\dot V}^n} = - {\phi ^n} \times {f^n} + C_b^n([\delta {K_a}] + T*[T{K_a}] + }\\& [\delta {M_a}] + T*[T{M_a}]){f^b} + \delta {V^n} \times (2\omega _{ie}^n + \omega _{en}^n) + \\& {V^n} \times (2\delta \omega _{ie}^n + \delta \omega _{en}^n) + B_a^n + T*TB_a^n{\rm{ + }}{\delta _a} \\& {\delta \dot L = \frac{{\delta {V_N}}}{{{R_N} + h}} - \delta h\frac{{{V_N}}}{{{{({R_N} + h)}^2}}}}\\& {\delta \dot \lambda = \frac{{\delta {V_E}}}{{{R_E} + h}}\sec L + \delta L\frac{{{V_E}}}{{{R_E} + h}}\tan L\sec L - \delta h\frac{{{V_E}\sec L}}{{{{({R_E} + h)}^2}}}}\\& {\delta \dot h = - \delta {V_D}}\\[-8pt] \end{split} $$ (5) 式中:
${V^n} = {\left[ {\begin{array}{*{20}{c}}{V_N^n}&{V_E^n}&{V_D^n} \end{array}} \right]^{\rm T}}$ 为IMU在n系下的速度;$L,\lambda ,h$ 分别表示纬度、经度和高度;${\phi ^n} = {\left[ {\begin{array}{*{20}{c}}{\phi _N^n}\;\;{\phi _E^n}\;\;{\phi _D^n} \end{array}} \right]^{\rm T}}$ 为IMU在n系下的姿态误差;$\omega _{ie}^n = {\left[ {\begin{array}{*{20}{c}}{{\omega _{ie}}\cos L}\;\;0\;\;{ - {\omega _{ie}}\sin L} \end{array}} \right]^{\rm T}}$ 为地球自转角速率在n系下的投影;$\omega _{en}^n = \Bigg[ {\dfrac{{{V_E}}}{{{R_E} + h}}}{ - \dfrac{{{V_N}}}{{{R_N} + h}}}\cdot {\dfrac{{{V_E}\tan L}}{{{R_E} + h}}} \Bigg]$ 为e系相对于n系的转动角速率;$ \delta [·] $ 表示为矢量$ [·] $ 的误差。将误差传播方差改写成矩阵形式,从而得到卡尔曼滤波器的状态方程如下:
$$ \dot X = FX + W(t) $$ (6) 其中,状态矢量
$ X $ 由45个分量组成:$$ \begin{array}{l} X = \left[ {\begin{array}{*{20}{c}} {{\phi _N}}&{{\phi _E}}&{{\phi _D}}&{\delta {V_N}}&{\delta {V_E}}&{\delta {V_D}}&{\delta L}&{\delta \lambda }&{\delta h} \end{array}} \right. \\ \begin{array}{*{20}{c}} {{B_{gx}}}&{{B_{gy}}}&{{B_{g{\textit{z}}}}}&{{B_{ax}}}&{{B_{ay}}}&{{B_{a{\textit{z}}}}}&{\delta {K_{gx}}}&{\delta {M_{gyx}}}&{\delta {M_{g{\textit{z}}x}}} \end{array} \\ \begin{array}{*{20}{c}} {\delta {K_{gy}}}&{\delta {M_{g{\textit{z}}y}}}&{\delta {K_{g{\textit{z}}}}}&{\delta {K_{ax}}}&{\delta {M_{ayx}}}&{\delta {M_{a{\textit{z}}x}}}&{\delta {M_{axy}}} \end{array} \\ \begin{array}{*{20}{c}} {\delta {K_{ay}}}&{\delta {M_{a{\textit{z}}y}}}&{\delta {M_{ax{\textit{z}}}}}&{\delta {M_{ay{\textit{z}}}}}&{\delta {K_{a{\textit{z}}}}}&{T{B_{ax}}} &{T{B_{ay}}} \end{array} \\ { {\begin{array}{*{20}{c}} {T{B_{a{\textit{z}}}}}&{T{K_{ax}}}&{T{K_{ay}}}&{T{K_{a{\textit{z}}}}}&{T{M_{ayx}}}&{T{M_{a{\textit{z}}x}}}&{T{M_{axy}}} \end{array}} } \\ \left.\begin{array}{*{20}{c}} {T{M_{a{\textit{z}}y}}}&{T{M_{ax{\textit{z}}}}}&{T{M_{ay{\textit{z}}}}}&{{r_x}}&{{r_y}}&{{r_{\textit{z}}}} \end{array}\right]^{\rm T}\\[-10pt] \end{array} $$ (7) 状态转移矩阵
$ F $ 由误差传播方差确定,$ W(t) $ 为激光陀螺和加速度计的输出白噪声。卡尔曼滤波器的观测方程表示为:
$$ Z = HX + v(t) $$ (8) 式中:
$\nu (t)$ 是量测噪声,可以被当作白噪声进行处理。文中选取速度误差和位置误差作为观测量,因此观测量
$ Z $ 和观测矩阵$ H $ 表示为:$$ Z = {\left[ {\begin{array}{*{20}{c}} {\delta {V_N}}&{\delta {V_E}}&{\delta {V_D}}&{\delta L}&{\delta \lambda }&{\delta h} \end{array}} \right]^{\rm {T}}} $$ (9) $$ H = {\left[ {\begin{array}{*{20}{c}} {{0_{3 \times 3}}}&{{I_{3 \times 3}}}&{{0_{3 \times 3}}}&{{0_{3 \times 36}}} \\ {{0_{3 \times 3}}}&{{0_{3 \times 3}}}&{{I_{3 \times 3}}}&{{0_{3 \times 36}}} \end{array}} \right]_{6 \times 45}} $$ (10) 式中:
$ {I_{3 \times 3}} $ 为三阶单位矩阵。 -
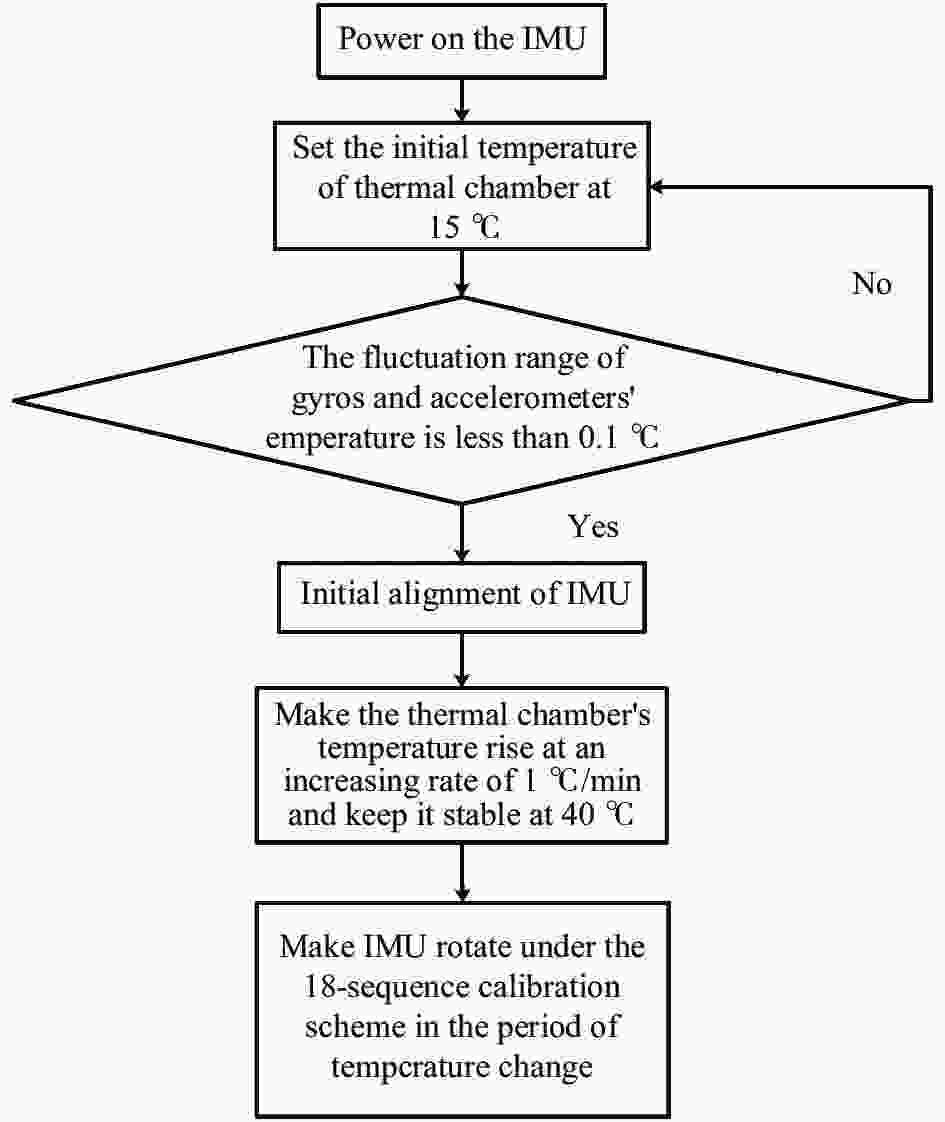
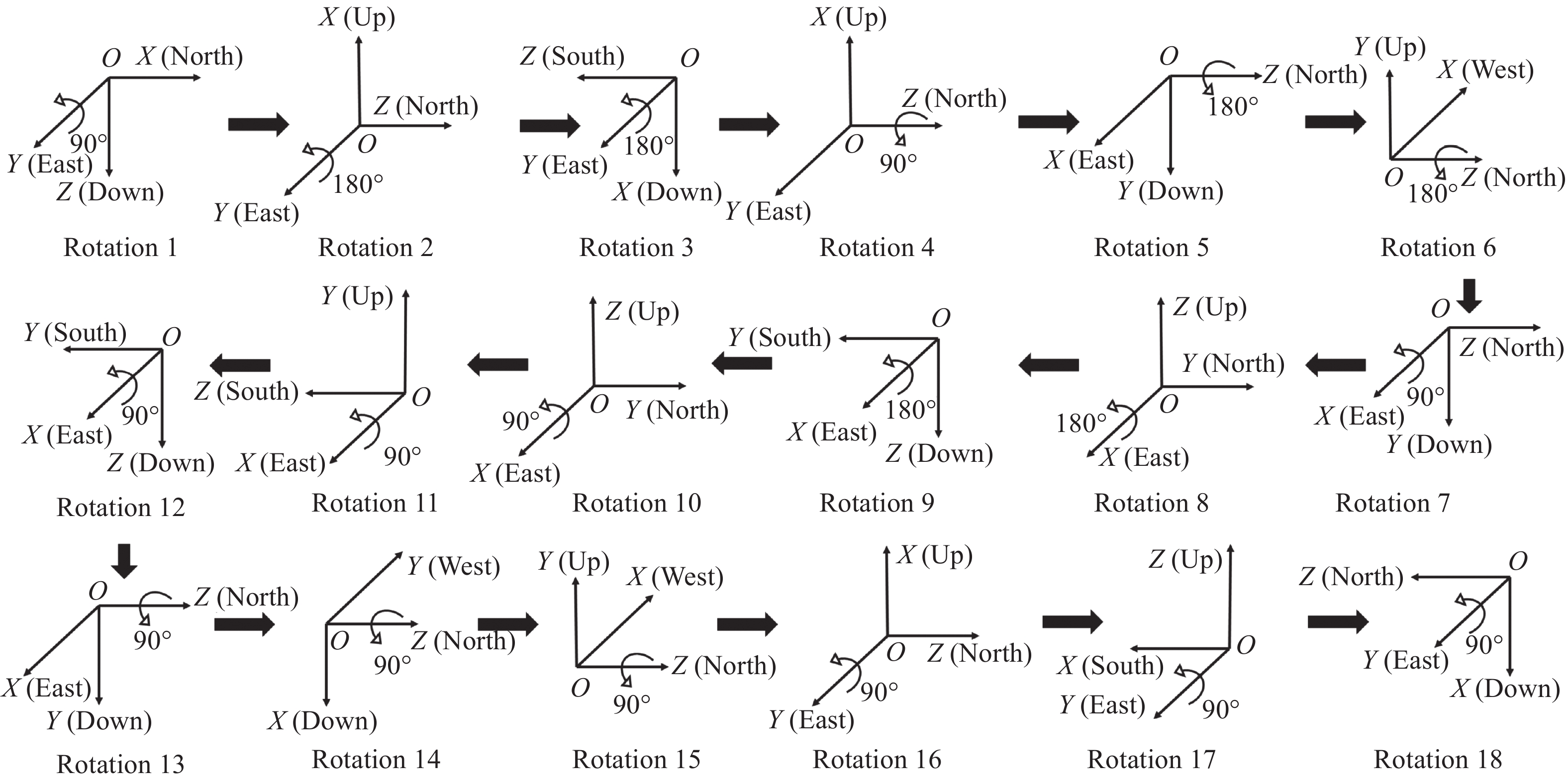
参考文献[5]设计了一种18次序标定路径,并且证明此路径可以有效标定出激光陀螺和加速度计的零偏、标度因数误差和安装误差。为了充分激励加速度计的温度误差系数,在此18次序标定路径的基础上,利用放置在转台上的温度控制试验箱控制标定过程的温度持续变化,标定路径的示意图如图1所示。
-
为了验证改进的18次序标定路径激励误差参数的有效性,基于分段线性定常系统(PWCS)对该标定路径进行可观测性分析[17-18]。对系统进行分段线性化,利用提取可观测性矩阵(SOM)代替总体可观测性矩阵(TOM),计算标定路径下各位置SOM的秩,结果如表1所示。
表 1 可观测性矩阵的秩
Table 1. Ranks of the SOM
Position Ranks of the SOM 0 12 1 18 2 23 3 26 4 32 5 35 6 38 7 41 8 42 9 44 10 44 11 45 … 45 18 45 由表1可以看出,经过11个次序的旋转后,SOM的秩达到45,等于滤波器的维数,证明系统在改进的18次序标定方案下完全可观,各项误差参数能够被有效地分离并辨识。
-
为了验证所提出的标定方法的可行性,该节进行仿真实验验证。仿真实验中IMU的初始速度设置为0,初始姿态角度设置为0,初始位置为(112.99°E,28.22°N),初始对准时间为20 min,仿真总时间设置为1.3 h,惯性器件的数据采样频率和Kalman滤波频率均为200 Hz。仿真初始设置加速度计表面温度为15 ℃,并以1 ℃/min的速率升温至40 ℃,后保持温度不变直至仿真实验结束。
表2展示了仿真实验中误差参数的预设值和估计值的对比。根据仿真结果,误差参数的估计残差均趋近于0,这表明文中提出的标定方法具有很高的估计精度。标定方法的可行性通过仿真实验得到了验证。仿真实验的卡尔曼滤波估计曲线如图2所示,可以看出:在标定结束时,所有误差参数收敛于一个特定取值范围内。

图 2 (a1)~(a4) 仿真实验温度误差系数和内杆臂参数的卡尔曼滤波估计曲线;(b1)~(b6) 仿真实验零偏、标度因数误差和安装误差的卡尔曼滤波估计曲线
Figure 2. (a1)-(a4) Kalman filtering estimation curves of temperature error coefficients and inner level arm parameters in simulation experiment; (b1)-(b6) Kalman filtering estimation curves of bias, scale factor error and installation error in simulation experiment
表 2 仿真实验误差参数的预设值和估计值
Table 2. Preset values and estimation values of error coefficients in simulation experiment
Error coefficients Preset Estimation Residual $\begin{gathered}{B_{gx} }/(^\circ) \cdot {\rm{h} }^{-1} \\{B_{gy} }/(^\circ)\cdot {\rm{h} }^{-1} \\{B_{gz} }/(^\circ) \cdot {\rm{h} }^{-1} \\ \end{gathered}$ 0.003
0.003
0.0030.0034
0.0031
0.00290.000 4
0.000 1
0.000 1Error coefficients Preset Estimation Residual $\begin{gathered}\delta {K_{gx} }/\rm ppm \\\delta {K_{gy} }/\rm ppm \\\delta {K_{gz} }/\rm ppm \end{gathered}$ 20
40
6020.17
40.02
60.010.17
0.02
0.01Error coefficients Preset Estimation Residual $\begin{array}{l}\delta {M}_{gyx}/('')\\ \delta {M}_{gzx}/('')\\ \delta {M}_{gzy}/('')\end{array}$ −61.88
41.25
−20.63−62.02
41.09
−20.540.14
0.16
0.09Error coefficients Preset Estimation Residual $\begin{gathered}{B_{ax} }/\text{μ} {\rm{g}} \\{B_{ay} }/\text{μ} {\rm{g}} \\{B_{az} }/\text{μ} {\rm{g}} \\ \end{gathered}$ 10
10
1010.02
10.01
-10.060.02
0.01
0.06Error coefficients Preset Estimation Residual $\begin{gathered}\delta {K_{ax}}/\rm ppm \\\delta {K_{ay}}/\rm ppm \\\delta {K_{az}}/\rm ppm \\ \end{gathered} $ 10
30
5010.06
30.08
50.060.06
0.08
0.06Error coefficients Preset Estimation Residual $\begin{array}{l}\delta {M}_{ayx}/('')\\ \delta {M}_{azx}/('')\\ \delta {M}_{axy}/('')\\ \delta {M}_{azy}/('')\\ \delta {M}_{axz}/('')\\ \delta {M}_{ayz}/('')\end{array}$ −41.25
20.62
61.88
−61.88
−20.62
41.25−41.20
20.59
61.79
−61.90
−20.69
41.280.05
0.03
0.09
0.02
0.07
0.03Error coefficients Preset Estimation Residual $\begin{gathered}T{B_{ax} }/ {\text{μ} {\rm{g} }\cdot^ {\circ} {\rm{C} } }^{-1} \\T{B_{ay} }/ {\text{μ} {\rm{g} }\cdot^ {\circ} {\rm{C} } } ^{-1}\\T{B_{az} }/ {\text{μ} {\rm{g} }\cdot^ {\circ} {\rm{C} } }^{-1} \\ \end{gathered}$ 0.2
1
20.198
0.999
1.9970.002
0.001
0.003Error coefficients Preset Estimation Residual $\begin{gathered}T{K_{ax} }/ { {\rm{ppm} }\cdot ^{\circ} {\rm{C} }^{-1} } \\T{K_{ay} }/ { {\rm{ppm} }\cdot ^{\circ} {\rm{C} }^{-1} } \\T{K_{az} }/ { {\rm{ppm} }\cdot ^{\circ} {\rm{C} }^{-1} } \\ \end{gathered}$ 1
2
31.001
2.002
2.9990.001
0.002
0.001Error coefficients Preset Estimation Residual $\begin{array}{l}T{M}_{ayx}/('')\cdot ^{\circ} {\rm{C} }^{-1}\\ T{M}_{azx}/('')\cdot ^{\circ} {\rm{C} }^{-1}\\T{M}_{axy}/('')\cdot ^{\circ} {\rm{C} }^{-1}\\ T{M}_{azy}/('')\cdot ^{\circ} {\rm{C} }^{-1}\\ T{M}_{axz}/('')\cdot ^{\circ} {\rm{C} }^{-1}\\ T{M}_{ayz}/('')\cdot ^{\circ} {\rm{C} }^{-1}\end{array}$ −0.1
0.2
0.3
0.4
0.5
−0.6−0.102
0.202
0.304
0.402
0.504
−0.6070.002
0.002
0.004
0.002
0.004
0.007Error coefficients Preset Estimation Residual $ \begin{gathered}{r_x}/\rm m \\{r_y}/\rm m \\{r_z}/\rm m \\ \end{gathered} $ 0.01
0.02
0.0050.0102
0.0199
0.00510.000 2
0.000 1
0.000 1 -
标定实验的实验系统如图3所示,包括高精度三轴转台、某型号IMU、温度控制试验箱、转台控制端和IMU数据采集装置。在IMU数据采集过程中,使用低通滤波器滤除激光陀螺原始信号中的高频抖动噪声。实验所用的三轴转台的角分辨率优于1″。标定实验所使用的IMU配备有三轴激光陀螺和三轴加速度计,IMU被放置在温度控制试验箱之中。激光陀螺和加速度计的零偏稳定性分别为0.005 (°)/h和20 μg。在每轴加速度计表面装配有一个铂电阻温度计来测量加速度计表面温度。
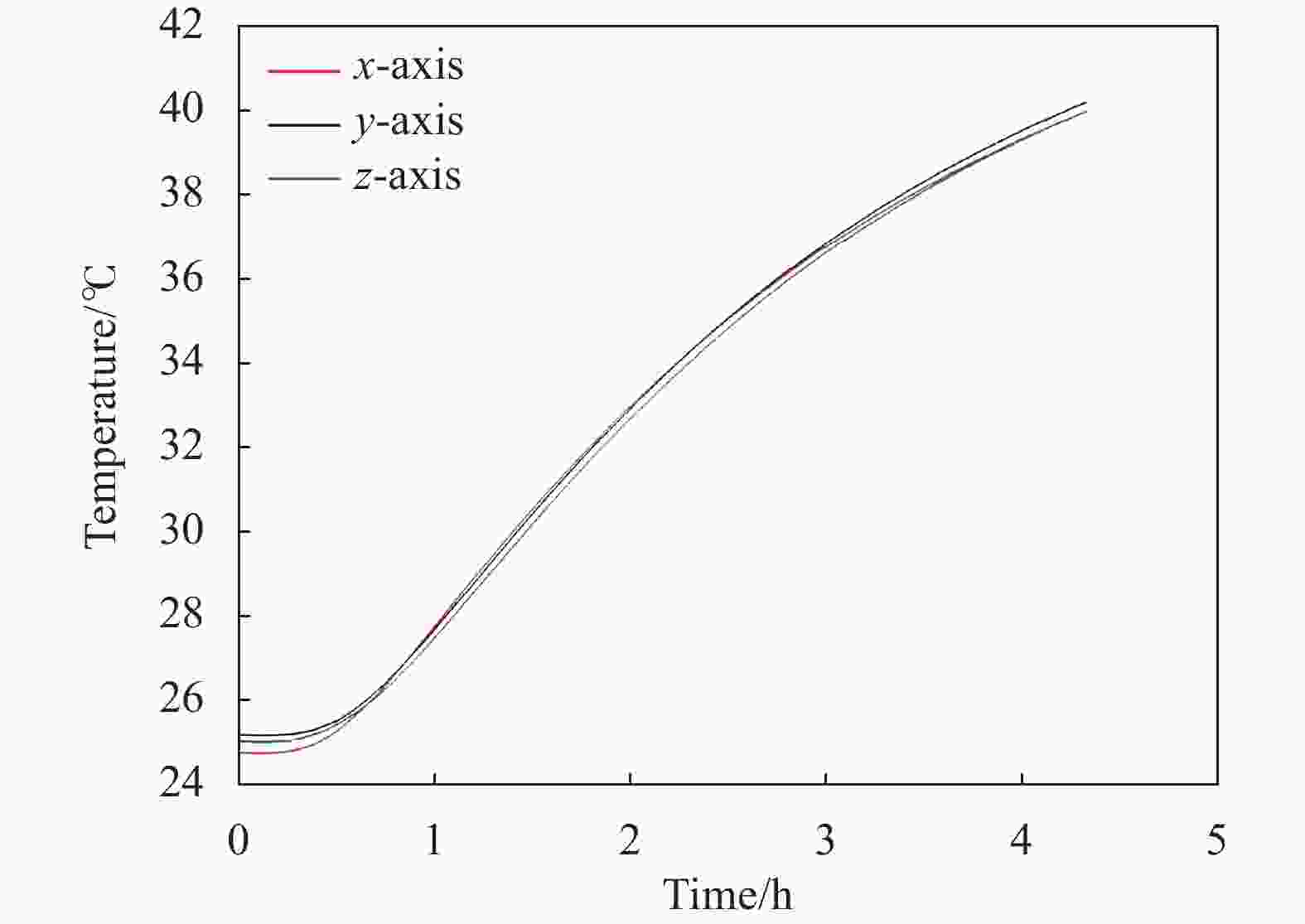
标定实验基于图4所示的流程来进行,加速度计表面温度的变化曲线如图5所示。考虑到在标定过程中温度误差系数需要相对较长的时间才能够收敛,因此将18次序标定路径循环4次。将温箱温度设置为自15 ℃开始以1 ℃/min的速率升温至40 ℃,之后温箱温度保持在40 ℃直至标定结束。由于温箱内热分布不均并且热传递会消耗一定时间,且IMU内部温度高于外界环境温度,加速度计表面温度升温过程会与温箱温度升温过程存在差异,因此在标定实验中通过铂电阻温度计实测温度对加速度计温度进行表征。
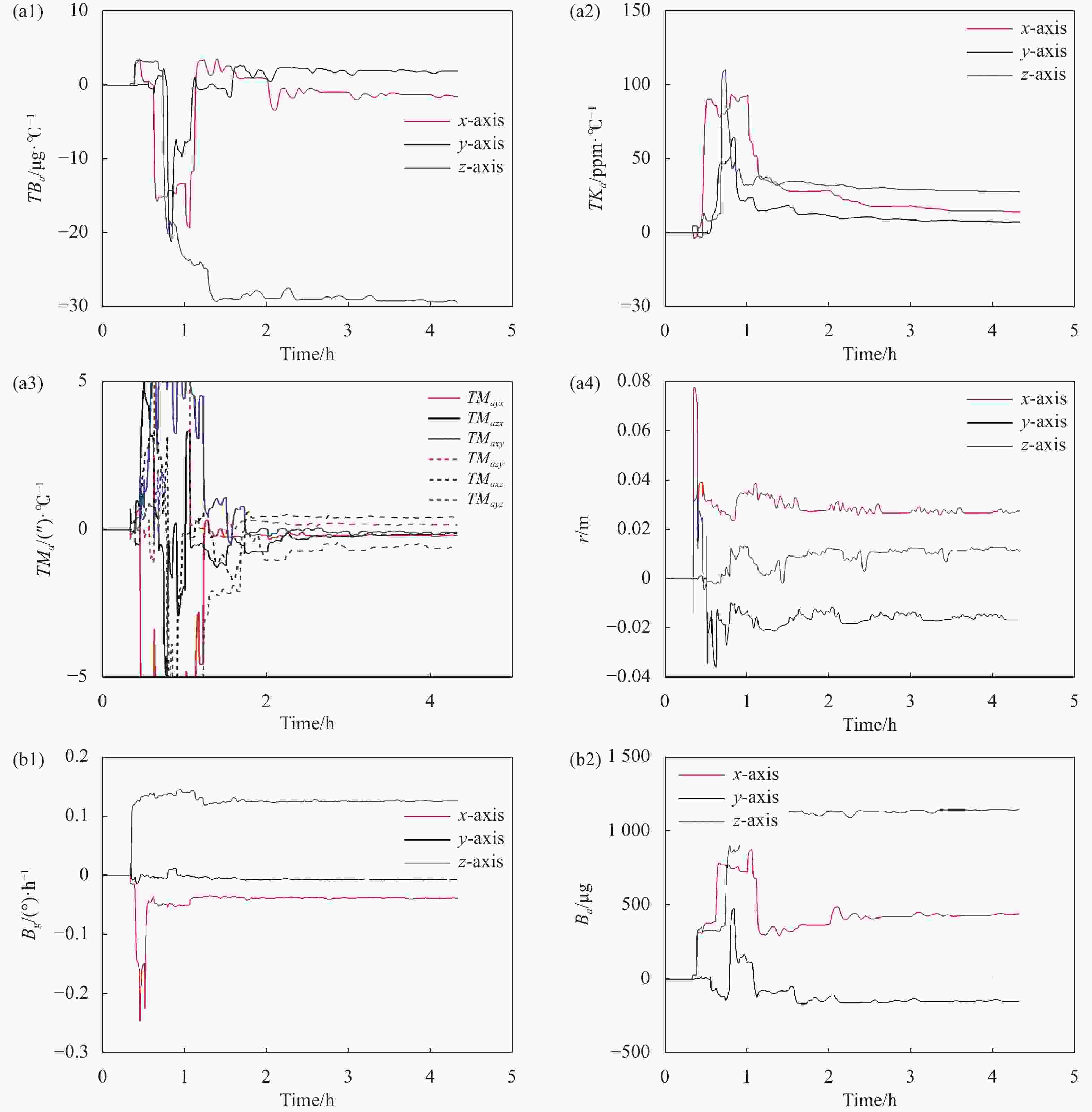
标定实验的卡尔曼滤波估计曲线如图6所示,所有的IMU误差参数在滤波结束阶段都能够收敛,表明文中提出的标定方法可以有效地标定出加速度计的温度误差系数与内杆臂参数,同时标定IMU标度因数误差、安装误差和零偏。各误差参数的标定值如表3所示。
表 3 误差参数的标定值
Table 3. Calibration value of error parameters
Error parameters Calibration value Gyro drifts/(°)·h−1 −0.098/−0.061/0.12 Gyro scale factor/rad·pulse−1 2.2609e-06/−2.2612e-06/−2.2611e-06 Gyro installation/(″) 842.70/−246.03/−1056.05/105.09/357.41/−309.24 Accelerometer biases/μg 368.6/−62.42/−126.5 Accelerometer scale factor/m·s−1·pulse−1 −2.8084e-04/2.7803e-04/2.7028e-04 Accelerometer installation/(″) 590.53/−244.94/−507.83/67.01/345.59/−148.38 Temperature coefficients of biases/μg·℃−1 −1.133/1.572/−31.68 Temperature coefficients of scale factor errors/ppm·℃−1 11.23/8.238/28.29 Temperature coefficients of installation/(″)·℃−1 −0.211/−0.089/−0141/0.121/0.325/−0.368 Inner level arm parameters/m 0.027/−0.017/0.011 
图 6 (a1)~(a4) 标定实验温度误差系数和内杆臂参数的滤波估计曲线; (b1)~(b6) 标定实验零偏,标度因数误差和安装误差的滤波估计曲线
Figure 6. (a1)-(a4) Kalman filtering estimation curves of temperature error coefficients and inner level arm parameters in calibration experiment; (b1)-(b6) Kalman filtering estimation curves of bias, scale factor error and installation error in calibration experiment
-
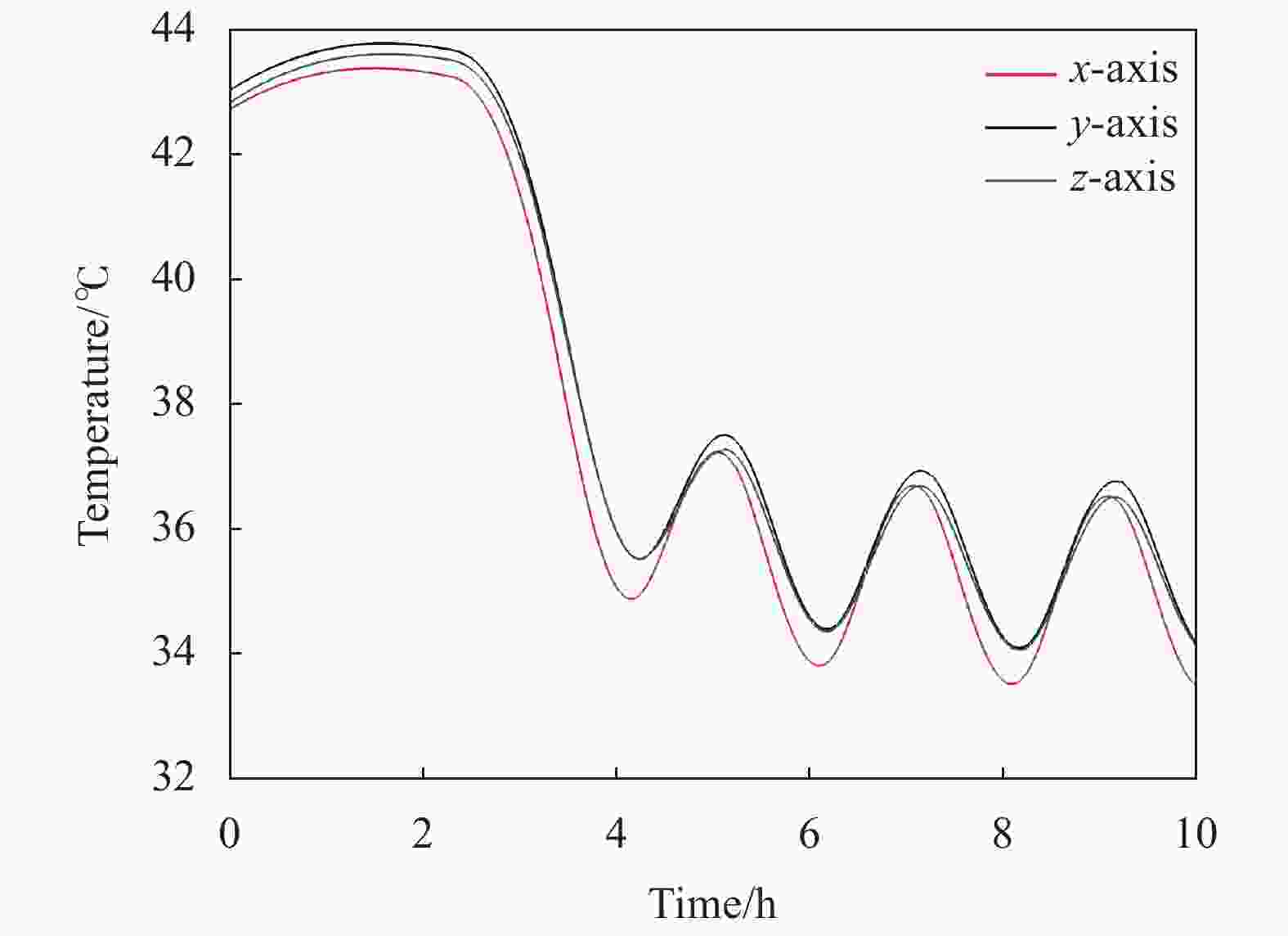
为了验证复杂误差参数的误差反馈效果,基于图3所示的三轴转台和温箱进行IMU变温摇摆导航实验。摇摆运动可以充分激励杆臂效应,用于验证内杆臂参数的反馈效果。转台摇摆方式如表4所示。温箱用于控制实验过程中加速度计表面温度的连续变化,用于验证温度误差系数的反馈效果。导航实验总时长为10 h。激光陀螺角增量和加速度计比力增量输出曲线如图7所示,加速度计表面温度变化曲线如图8所示。
表 4 摇摆运动方式
Table 4. Swing mode
Vibration axis (IMU) Amplitude/(°) Frequency/Hz Swing mode 1
(5-7.3 h)x-axis 2 0.3 y-axis 4 0.2 z-axis 6 0.1 Swing mode 2
(8.6-10 h)x-axis 6 0.15 y-axis 8 0.2 z-axis 10 0.1 
图 7 (a1)~(a4) 导航实验激光陀螺角增量输出曲线; (b1)~(b6) 导航实验加速度计比力增量输出曲线
Figure 7. (a1)-(a4) Output curves of angular increment of laser gyros in navigation experiment; (b1)-(b6) Output curves of specific force increment of accelerometers in navigation experiment
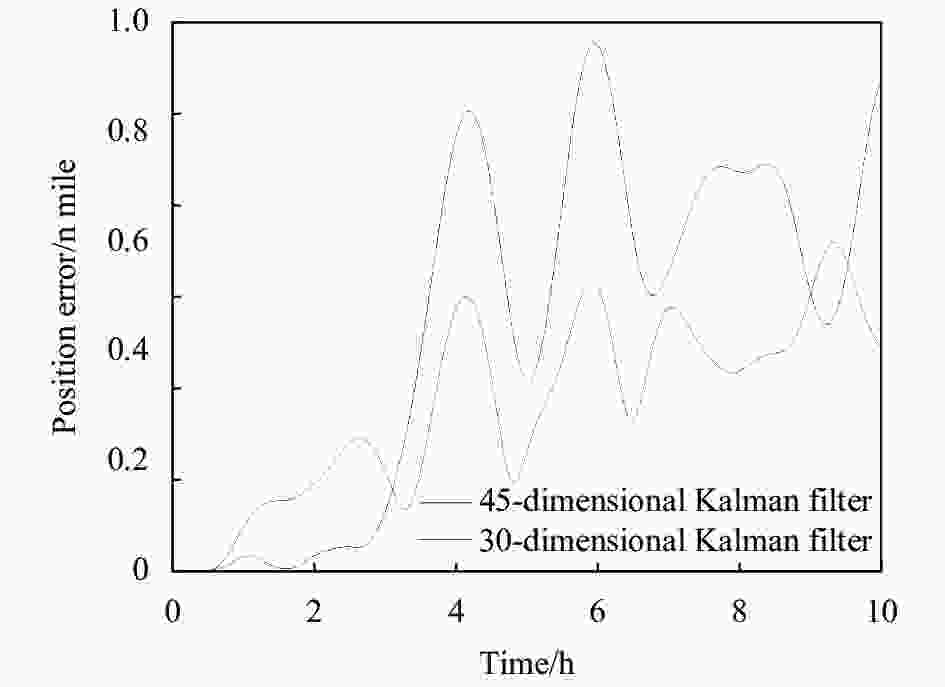
为了验证在导航实验中对温度误差系数和内杆臂参数的误差补偿效果,在相同的18次序标定路径下采用不考虑温度误差系数和内杆臂参数的30维滤波器进行系统级标定,并利用30维滤波器和45维滤波器分别得到一组标定结果,将两组标定结果同时进行导航解算,得出导航实验的水平定位误差如图9所示,基于30维滤波器标定的导航最大水平定位误差超过0.96 n mile,而基于45维滤波器标定的10 h导航最大水平定位误差优于0.60 n mile,导航精度提升了37.5%。由此可见,采用文中提出的复杂误差参数的系统级标定方法对IMU标定参数进行误差反馈,可以有效改善惯导系统的导航精度。
-
文中针对捷联惯导系统复杂误差参数的标定问题,提出了一种基于45维卡尔曼滤波器的系统级标定方法。算法分析与实验结果表明:
(1)文中所建立的IMU误差模型能够实现温度误差系数和内杆臂参数的标定与补偿,为研究更高阶温度模型的建立和复杂误差源的标定提供了新的方法。
(2)为了同时标定出温度误差系数和内杆臂参数,文中设计了一个45维的卡尔曼滤波器,并基于三轴转台与温箱,提出了一种控制温度变化的改进18次序标定路径。仿真实验表明,提出的标定方案具有可行性。
(3)为了验证文中提出的标定方案的误差补偿效果,开展了变温摇摆导航实验,实验结果表明,对标定参数进行多误差源补偿后,10 h导航水平最大定位误差为0.60 n mile,相比没有经过温度误差系数和内杆臂参数补偿的标定参数,导航精度提升了37.5%。
System-level calibration method for complex error coefficients of strapdown inertial navigation system
-
摘要: 重点研究捷联惯导系统复杂误差模型的建立,提出了一种新的包含加速度计内杆臂参数和温度误差系数的系统级标定方法。该方法基于45维卡尔曼滤波器对误差参数进行辨识估计,并通过温度控制试验箱控制标定过程中的温度变化。仿真实验表明该方法能够同时标定出激光陀螺和加速度计的零偏、标度因数误差、安装误差以及加速度计的内杆臂参数和温度误差系数。导航实验结果表明,对标定参数进行多误差源补偿之后,10 h导航实验水平最大定位误差为0.6 n mile (1 n mile=1.852 km),相较于不经过补偿,导航精度提升了37.5%。Abstract: The establishment of a complex error model of strapdown inertial navigation system is researched, and a new system-level calibration method isproposed, which includes the inner level arm parameters of the accelerometer and temperature error coefficients. The method is based on the 45-dimensional Kalman filter to identify and estimate the error parameters, and the temperature change in the calibration process is controlled by a temperature control test chamber. Simulation experiments show that this method can simultaneously calibrate the constant drift, scale factor error, installation error of the laser gyroscope and accelerometer, as well as the inner level arm parameters and temperature coefficients of the accelerometer. The results of the navigation experiment show that when using the calibration parameters compensated for multiple error sources, the maximum positioning error of the navigation for 10 h is 0.6 n miles. The navigation accuracy is improved by 37.5% compared to that without compensation.
-
图 2 (a1)~(a4) 仿真实验温度误差系数和内杆臂参数的卡尔曼滤波估计曲线;(b1)~(b6) 仿真实验零偏、标度因数误差和安装误差的卡尔曼滤波估计曲线
Figure 2. (a1)-(a4) Kalman filtering estimation curves of temperature error coefficients and inner level arm parameters in simulation experiment; (b1)-(b6) Kalman filtering estimation curves of bias, scale factor error and installation error in simulation experiment
图 6 (a1)~(a4) 标定实验温度误差系数和内杆臂参数的滤波估计曲线; (b1)~(b6) 标定实验零偏,标度因数误差和安装误差的滤波估计曲线
Figure 6. (a1)-(a4) Kalman filtering estimation curves of temperature error coefficients and inner level arm parameters in calibration experiment; (b1)-(b6) Kalman filtering estimation curves of bias, scale factor error and installation error in calibration experiment
表 1 可观测性矩阵的秩
Table 1. Ranks of the SOM
Position Ranks of the SOM 0 12 1 18 2 23 3 26 4 32 5 35 6 38 7 41 8 42 9 44 10 44 11 45 … 45 18 45 表 2 仿真实验误差参数的预设值和估计值
Table 2. Preset values and estimation values of error coefficients in simulation experiment
Error coefficients Preset Estimation Residual $\begin{gathered}{B_{gx} }/(^\circ) \cdot {\rm{h} }^{-1} \\{B_{gy} }/(^\circ)\cdot {\rm{h} }^{-1} \\{B_{gz} }/(^\circ) \cdot {\rm{h} }^{-1} \\ \end{gathered}$ 0.003
0.003
0.0030.0034
0.0031
0.00290.000 4
0.000 1
0.000 1Error coefficients Preset Estimation Residual $\begin{gathered}\delta {K_{gx} }/\rm ppm \\\delta {K_{gy} }/\rm ppm \\\delta {K_{gz} }/\rm ppm \end{gathered}$ 20
40
6020.17
40.02
60.010.17
0.02
0.01Error coefficients Preset Estimation Residual $\begin{array}{l}\delta {M}_{gyx}/('')\\ \delta {M}_{gzx}/('')\\ \delta {M}_{gzy}/('')\end{array}$ −61.88
41.25
−20.63−62.02
41.09
−20.540.14
0.16
0.09Error coefficients Preset Estimation Residual $\begin{gathered}{B_{ax} }/\text{μ} {\rm{g}} \\{B_{ay} }/\text{μ} {\rm{g}} \\{B_{az} }/\text{μ} {\rm{g}} \\ \end{gathered}$ 10
10
1010.02
10.01
-10.060.02
0.01
0.06Error coefficients Preset Estimation Residual $\begin{gathered}\delta {K_{ax}}/\rm ppm \\\delta {K_{ay}}/\rm ppm \\\delta {K_{az}}/\rm ppm \\ \end{gathered} $ 10
30
5010.06
30.08
50.060.06
0.08
0.06Error coefficients Preset Estimation Residual $\begin{array}{l}\delta {M}_{ayx}/('')\\ \delta {M}_{azx}/('')\\ \delta {M}_{axy}/('')\\ \delta {M}_{azy}/('')\\ \delta {M}_{axz}/('')\\ \delta {M}_{ayz}/('')\end{array}$ −41.25
20.62
61.88
−61.88
−20.62
41.25−41.20
20.59
61.79
−61.90
−20.69
41.280.05
0.03
0.09
0.02
0.07
0.03Error coefficients Preset Estimation Residual $\begin{gathered}T{B_{ax} }/ {\text{μ} {\rm{g} }\cdot^ {\circ} {\rm{C} } }^{-1} \\T{B_{ay} }/ {\text{μ} {\rm{g} }\cdot^ {\circ} {\rm{C} } } ^{-1}\\T{B_{az} }/ {\text{μ} {\rm{g} }\cdot^ {\circ} {\rm{C} } }^{-1} \\ \end{gathered}$ 0.2
1
20.198
0.999
1.9970.002
0.001
0.003Error coefficients Preset Estimation Residual $\begin{gathered}T{K_{ax} }/ { {\rm{ppm} }\cdot ^{\circ} {\rm{C} }^{-1} } \\T{K_{ay} }/ { {\rm{ppm} }\cdot ^{\circ} {\rm{C} }^{-1} } \\T{K_{az} }/ { {\rm{ppm} }\cdot ^{\circ} {\rm{C} }^{-1} } \\ \end{gathered}$ 1
2
31.001
2.002
2.9990.001
0.002
0.001Error coefficients Preset Estimation Residual $\begin{array}{l}T{M}_{ayx}/('')\cdot ^{\circ} {\rm{C} }^{-1}\\ T{M}_{azx}/('')\cdot ^{\circ} {\rm{C} }^{-1}\\T{M}_{axy}/('')\cdot ^{\circ} {\rm{C} }^{-1}\\ T{M}_{azy}/('')\cdot ^{\circ} {\rm{C} }^{-1}\\ T{M}_{axz}/('')\cdot ^{\circ} {\rm{C} }^{-1}\\ T{M}_{ayz}/('')\cdot ^{\circ} {\rm{C} }^{-1}\end{array}$ −0.1
0.2
0.3
0.4
0.5
−0.6−0.102
0.202
0.304
0.402
0.504
−0.6070.002
0.002
0.004
0.002
0.004
0.007Error coefficients Preset Estimation Residual $ \begin{gathered}{r_x}/\rm m \\{r_y}/\rm m \\{r_z}/\rm m \\ \end{gathered} $ 0.01
0.02
0.0050.0102
0.0199
0.00510.000 2
0.000 1
0.000 1表 3 误差参数的标定值
Table 3. Calibration value of error parameters
Error parameters Calibration value Gyro drifts/(°)·h−1 −0.098/−0.061/0.12 Gyro scale factor/rad·pulse−1 2.2609e-06/−2.2612e-06/−2.2611e-06 Gyro installation/(″) 842.70/−246.03/−1056.05/105.09/357.41/−309.24 Accelerometer biases/μg 368.6/−62.42/−126.5 Accelerometer scale factor/m·s−1·pulse−1 −2.8084e-04/2.7803e-04/2.7028e-04 Accelerometer installation/(″) 590.53/−244.94/−507.83/67.01/345.59/−148.38 Temperature coefficients of biases/μg·℃−1 −1.133/1.572/−31.68 Temperature coefficients of scale factor errors/ppm·℃−1 11.23/8.238/28.29 Temperature coefficients of installation/(″)·℃−1 −0.211/−0.089/−0141/0.121/0.325/−0.368 Inner level arm parameters/m 0.027/−0.017/0.011 表 4 摇摆运动方式
Table 4. Swing mode
Vibration axis (IMU) Amplitude/(°) Frequency/Hz Swing mode 1
(5-7.3 h)x-axis 2 0.3 y-axis 4 0.2 z-axis 6 0.1 Swing mode 2
(8.6-10 h)x-axis 6 0.15 y-axis 8 0.2 z-axis 10 0.1 -
[1] 石文峰, 王省书, 郑佳兴, 等. 激光陀螺捷联惯导系统多位置系统级标定方法[J]. 红外与激光工程, 2016, 45(11): 99-106. doi: 10.3788/IRLA201645.1106004 Shi Wenfeng, Wang Xingshu, Zheng Jiaxing, et al. Multi-position systematic calibration method for RLG-SINS [J]. Infrared and Laser Engineering, 2016, 45(11): 1106004. (in Chinese) doi: 10.3788/IRLA201645.1106004 [2] Ren Qian, Wang Bo, Deng Zhihong, et al. Amulti-position self-calibration method for dual-axis rotational inertial navigation system [J]. Sensors & Actuators A: Physical, 2014, 219: 24-31. [3] Tuukka Nieminen, Jari Kangas, Saku Suuriniemi, et al. An enhanced multi-position calibration method for consumer-grade inertial measurement units applied and tested [J]. Measurement Science and Technology, 2010, 21: 105204. doi: 10.1088/0957-0233/21/10/105204 [4] Zhang Hongliang, Wu Yuanxin, Wu Wenqi, et al. Improved multi-position calibration for inertial measurement units [J]. Measurement Science and Technology, 2010, 21: 015107. doi: 10.1088/0957-0233/21/1/015107 [5] Camberlein L, Mazzanti F. Calibration technique for laser gyro strapdowninertial navigation systems[C]//Symposium Gyro Technology, 1985. [6] 江奇渊, 汤建勋, 韩松来, 等. 36维Kalman滤波的激光陀螺捷联惯导系统级标定方法[J]. 红外与激光工程, 2015, 44(05): 1579-1586 doi: 10.3969/j.issn.1007-2276.2015.05.033 Jiang Qiyuan, Tang Jianxun, Han Songlai, et al. Systematic calibration method based on 36-dimension Kalman filter for laser gyro SINS [J]. Infrared and Laser Engineering, 2015, 44(5): 1579-1586. (in Chinese) doi: 10.3969/j.issn.1007-2276.2015.05.033 [7] 于旭东, 王宇, 张鹏飞, 等. 单轴旋转惯导系统中陀螺漂移的精确校准[J]. 光学精密工程, 2012, 20(06): 1201-1207. Yu Xudong, Wang Yu, Zhang Pengfei, et al. Calibration of RLG driftin single-axisrotation INS [J]. Optics and Precision Engineering, 2012, 20(6): 1201-1207. (in Chinese) [8] 刘冰, 任继山, 白焕旭, 等. 基于高阶卡尔曼滤波的激光捷联惯导系统级标定方法[J]. 导弹与航天运载技术, 2017(04): 90-94. Liu Bing, Ren Jishan, Bai Huanxu, et al. Systematic calibration method based on high-order Kalman filter for laser gyro SINS [J]. Missiles and Space Vehicles, 2017(4): 90-94. (in Chinese) [9] 张红良. 陆用高精度激光陀螺捷联惯导系统误差参数估计方法研究[D]. 长沙: 国防科学技术大学, 2010. Zhang Hongliang. Research on the methods for error parameter estimation of the land high-precision RLG strapdown inertial navigation system [D]. Changsha: National University of Defense Technology, 2010. (in Chinese) [10] 于海龙. 提高强振动环境下激光陀螺捷联惯导系统精度的方法研究[D]. 长沙: 国防科学技术大学, 2012. Yu Hailong. Research on the methods for improving the accuracy of Laser Gyro SINS in vibration environment [D]. Changsha: National University of Defense Technology, 2012. (in Chinese) [11] Gao Jingmin, Zhang Kebei, Chen Fubin, et al. Temperature characteristics and error compensation for quartz flexible accelerometer [J]. International Journal of Automation and Computing, 2015, 12(5): 540-550. doi: 10.1007/s11633-015-0899-5 [12] Pan Yingjun, Li Leilei, Ren Chunhua, et al. Study on the compensation for a quartz accelerometer based on a wavelet neural network [J]. Measurement Science and Technology, 2010, 21(10): 105202. doi: 10.1088/0957-0233/21/10/105202 [13] Ban Jingxuan, Wang Lei, Liu Zengjun, et al. Self-calibration method for temperature errors in multi-axis rotational inertial navigationsystem [J]. Optics Express, 2020, 28(6): 8909-8923. doi: 10.1364/OE.384905 [14] Weng Jun. Multi-position continuous rotate-stop fast temperature parameters estimation method of flexible pendulum accelerometer triads [J]. Measurement, 2020, 169: 108372. [15] 江奇渊, 汤建勋, 袁保伦, 等. 激光陀螺捷联惯导尺寸效应误差分析与补偿[J]. 红外与激光工程, 2015, 44(04): 1110-1114. doi: 10.3969/j.issn.1007-2276.2015.04.002 Jiang Qiyuan, Tang Jianxun, Yuan Baolun, et al. Analysis and compensation for size effect error of laser gyro Strapdown Inertial Navigation System [J]. Infraredand Laser Engineering, 2015, 44(4): 1110-1114. (in Chinese) doi: 10.3969/j.issn.1007-2276.2015.04.002 [16] 王子卉, 程向红, 范时秒. 基于双轴转台的捷联惯性导航系统8位置系统级标定方法[J]. 中国惯性技术学报, 2019, 27(01): 23-31. Wang Zihui, Cheng Xianghong, Fan Shimiao. Eight-position systematic calibration method for SINS based on two-axis turntable with temperature compensation [J]. Journal of Chinese Inertial Technology, 2019, 27(1): 23-31. (in Chinese) [17] Cao Yuan, Cai Hong, Zhang Shifeng, et al. A new continuous self-calibration scheme for a gimbaled inertial measurement unit [J]. Measurement Science and Technology, 2012, 23(1): 015103. doi: 10.1088/0957-0233/23/1/015103 [18] 程向红, 万德钧, 仲巡. 捷联惯导系统的可观测性和可观测度研究[J]. 东南大学学报, 1997, {4}(06): 8-13. Cheng Xianghong, Wan Dejun, Zhong Xun. Study on observability and its degree of strapdown inertial navigation system [J]. Journal of Southeast University, 1997, 4(6): 8-13. (in Chinese) -







 下载:
下载: