-
作为常用的非接触测温方法，红外热像仪在切削加工的温度测量中得到了越来越多的应用。红外热像仪能够远程测温，这一特点大大降低了测量环境对测温方法的制约，国内外众多学者采用红外热像仪进行切削温度的测量。
盛精等人[1]研究了硬质合金刀具加工沉淀硬化不锈钢的最佳切削温度，采用红外热成像法获得切削温度数据。葛英飞等人[2]采用红外测温仪测量切削温度，研究了重载荷铣削焊接铝薄壁空心结构的切削温度影响因素。Piotr等人[3]采用红外热像仪，研究了切削参数(切削速度和进给速度)对切削温度的影响，认为在刀具旋转时，红外测温法具有较好的效果。Kumar等人[4]采用红外测温装置，研究了无涂层和带PVD制备的AlTiN涂层Al2O3/TiCN混合陶瓷刀具硬切削AISI52100钢(62HRC)的切削温度。
在切削温度测量过程中，发射率设定对红外热像仪测量结果的准确性具有决定性的影响[5-6]，而发射率也受外界因素的影响。
国内外学者对影响物体发射率的因素进行了较多的研究。柯维娜等人[7]模拟并讨论了不同角度测量时，实际金属表面发射率的变化趋势，结果表明：表面光滑金属的法向发射率在入射角大于80°时变化剧烈。Shi等人[8-9]认为表面氧化环境下温度对DC01钢和黄铜的发射率有一定影响。Wang等人[10]对Q235钢和T2铜表面发射率的影响因素进行了研究。结果表明：温度和表面粗糙度的增加使得发射率随之增加。Jo等人[11]利用具有多重余弦函数的傅里叶级数随机生成表面轮廓，预测了粗糙氧化表面的发射率，并通过实验证实了表面粗糙度对SA508钢发射率的影响。Lan等人[12]建立了非稳态温度场模型来分析物体表面发射率的影响以提高红外热像仪测温精度，但该模型所针对的温度范围较低，不适合于切削加工这种高温工况。Hartsfield等人[13]认为材料表面发射率的增加取决于几何形状和角度，并通过特定金属的表面粗糙度数据进行了发射率的预测。赵晚梦等人[14]采用红外热像仪对Ti6Al4V的发射率进行研究，结果表明：测量角度、温度、波长和氧化程度等因素对材料发射率都有明显的影响。
为准确测量温度，必须在测温之前进行设定发射率的准确标定。国内外学者在发射率测量方面也有较多的成果发表。早期有学者[12-15]利用能量守恒定律间接测量发射率。也有学者[16-18]利用基尔霍夫定律通过比较黑体与实际物体的辐射能量来计算发射率。但这两种方法相对复杂，对环境要求苛刻。根据红外热像仪的测温原理，结合热电偶和红外热像仪能够较为快速准确的获取被测物体的发射率。白敬晨等人[19]结合热电偶和红外热像仪进行了发射率测量，并结合热像仪公式对测量误差进行了计算。王中任等人[20]采用结合热电偶与红外热像仪的方法对45钢棒料进行了发射率的测定。Zhang等人[21]从热像仪测量角场和背景温度两方面研究了测量距离对红外热像仪的测量精度的影响，并提出了相应的温度补偿方法。李文军[22]也采用结合热电偶和红外热像仪的方法在70~250 ℃内对绝缘胶带的发射率进行了测试。廖盼盼等人[23]研究了热像仪测温精度的影响因素，认为需要对红外热像仪进行距离补偿以减小测温误差。
从上述研究可以看出：目前对发射率的研究还没有统一的结论，研究的温度水平大多不高于500 ℃。在切削过程中，金属的塑性变形和刀具的摩擦使得切削温度处在很高的水平，有些温度甚至超过了1000 ℃。而在发射率测定方面，对高温条件下发射率的研究极少。
SiCp/Al复合材料作为典型的颗粒增强复合材料，以铝合金作为基体，SiC颗粒作为增强相与铝基体物理混合形成。颗粒的加入能够提高基体的物理性能如强度、硬度、耐磨性及高温性能等。但同时会使得切削热增加和刀具磨损加快，导致切削温度较高。目前大多采用红外热像仪进行SiCp/Al复合材料切削温度的测量。然而国内外对该材料发射率的研究较少。
因此，文中开展切削加工红外热像仪精确测温设定发射率确定的实验研究。以SiCp/Al复合材料为被测对象，首先进行温度标定实验，研究设定发射率对红外热像仪测温精度的影响。其次通过析因实验分析设定发射率的影响因素。最后通过正交实验研究各因素对设定发射率的影响程度，并进行经验公式拟合和实验验证。需要说明的是，文中所说的设定发射率是指采用红外热像仪进行温度测量时发射率的设定值，不同于物体本身的发射率，与被测物体本身的物理特性及热像仪的能量接收都有关系。
-
采用热电偶和红外热像仪同时测温的方式进行实验。加热装置采用最高可加热到1000 ℃的可调式电阻炉，热电偶为电阻炉内置的数显标准热电偶，其显示的温度即为实际温度。热像仪采用发射率可调的Fluke-Ti640热像仪。表1列出了红外热像仪的主要技术参数。以SiCp/Al颗粒增强复合材料为实验对象，体分比为45%，SiC颗粒平均尺寸为5 μm，基体为2024Al，表2给出了被测试件的基本热性能参数。试件为厚度h=1.5 mm的薄片，其表面粗糙度Ra=0.4 μm。实验装置如图1所示。
表 1 Fluke-Ti640红外热像仪的主要技术参数
Table 1. Main technical parameters of fluke-Ti640 infrared thermal imager
Project Content Wavelength/µm 7.5−14 Frame rate/Hz 60 Temperature range/℃ −40 − +1200 Accuracy/℃ ±0.1 
图 1 实验装置
Figure 1. Experimental device
表 2 SiCp/Al复合材料基本性能
Table 2. Basic properties of SiCp/Al composite
Parameter 2024Al SiC Thermal conductivity/(W·m−1·K−1） 180 81 Specific heat capacity/(J·kg−1·K−1） 880 427 Volume fraction 55% 45% Density/(kg·m−3) 2.7×103 3.13×103 Poisson ratio 0.34 0.14 Thermal expansion coefficient/K−1 23.6×10−6 4.9×10−6 实验温度范围为100~700 ℃，每隔100 ℃进行一次测量。实验时，首先将试件放入电阻炉中进行加热。用热电偶进行监测，达到测量点后保温15 min。由于热像仪不能直接测量炉内试件的温度，所以测量时需要将试件取出，为了减少试件取出时的热量损失，测量时试件尽量靠近炉口，且热像仪需要快速进行拍摄，每次测量过程不超过1 s，以确保试件试件温度基本不变。将试件取出，采用热像仪在试样的正上方进行垂直拍摄，观测距离设置为250 mm(该型号热像仪的最短聚焦距离)。对于SiCp/Al颗粒增强复合材料，通过红外测温仪使用手册查出其推荐发射率为0.24~0.36。首先按照通常的设定方法取推荐值的中间值，即将发射率设为0.3。然后按照±10%和±20%的比率对热像仪设置不同发射率进行温度测量。因此，对每个温度测量点，采用5组发射率（0.24、0.27、0.3、0.33、0.36）分别测温并记录结果。
-
图2为当发射率设为0.3时测量值与实际温度的差值。可以看出，当被测材料温度小于500 ℃时，热像仪的测温结果与实际温度差异很小，这说明按照推荐发射率中值进行发射率设定可行。但当温度高于500 ℃时，测量温度与实际温度产生了明显的差异，测量温度明显高于实际温度。
这是因为，金属材料的电阻随温度增大而增大。随着金属电阻的增大，金属的折射率和消光系数都随之下降，同时穿透深度也随之增大，辐射能量在金属表面的反射减少，从而增大了其表面发射率[24]。另一方面随着材料温度升高导致材料表面发生氧化，发射率随着氧化程度加剧而增加[25]。
从实验中也可以发现，当试件温度超过500 ℃时，试件的表面发生了氧化，使得试件的发射率发生变化，导致设定发射率下所测得的温度与实际温度产生较大差异。图3（a）、（b）所示分别为加热到500 ℃之后和500 ℃之前被测材料的实物图，可以看到明显的氧化现象。
图 2 发射率为0.3时测量温度与实际温度的差异
Figure 2. Difference between measured and actual temperature when the emissivity is 0.3
图 3 被测实物
Figure 3. Measured object
根据实验结果对热像仪测量结果进行修正：
$$ {T}_{实}={T}_{测}-{T}_{偏} $$ (1) 式中：T实为试件实际温度(℃)；T测为热像仪测量温度(℃)；T偏为温度偏差，对于文中的SiCp/Al颗粒增强复合材料T偏=218.5 ℃。
不同设定发射率时红外热像仪的测温曲线如图4所示。由曲线可以看出，设定发射率值越大，热像仪的测量温度越低，在温度小于500 ℃时，实际值与测量值的差异随着温度的升高有增大的趋势，但不明显，而当温度高于500 ℃时，差异明显增大。当实际温度达到700 ℃时，误差最大，达到52.4%。
图 4 不同发射率设定对测量温度的影响
Figure 4. Effect of different emissivities on the measured temperature
-
测温试验进一步表明，采用红外测温仪进行温度测量时，发射率设定直接影响测量结果，因此，文中进一步通过析因实验分析设定发射率的影响因素。
设定发射率除受温度影响外，还受表面粗糙度等其他因素的影响。
首先，对于粗糙表面，一方面，多次漫反射的发生增加了物体表面对红外辐射吸收的机会，从而增加了材料的吸收率；另一方面，粗糙表面在微观上呈现出的不规则表面使辐射体的相对辐射面积增大，从而增加了辐射能，相应的发射率也增大。所以材料的发射率一般会随着表面粗糙度的增大而增大[13-26]。
其次，在使用红外热像仪测量温度时，被测物体到热像仪物镜的距离d影响测量角场w。如图5所示，角场w随着距离的增大而减小。
图 5 角场w与测量距离d的几何关系[21]
Figure 5. Geometric relationship between angle field w and measurement distance d
根据热像仪的测量原理，角场w影响热像仪的输出电压为：
$$ V^{\prime}\left(T_{0}\right)=\varepsilon R_{\max } A_{d} c_{1} \sin ^{2} u_{m}^{\prime} \cos ^{4} w \int_{\lambda_{x}}^{\lambda_{1}} \frac{\tau(\lambda) s(\lambda)}{\lambda^{5}\left({\rm{e}}^{\frac{5_{x}}{x_{0}}}-1\right)} $$ (2) 式中：ε为发射率；Rmax为红外热像仪的最大灵敏度；Ad为探测面积；
$ {\mu '_m} $ 为物镜孔径角；λ1和λ2为热像仪的工作波段；c1为第一辐射常数；c2为第二辐射常数；τ(λ)为光学系统透过率；s(λ)为被测物体的绝对温度。输出电压与输出温度之间满足公式(3)：
$$ V'({T_0}) = \left( {\frac{1}{{{K_1}}}\sum\limits_{k = 0}^n {{a_k}{T_k}} } \right) - {K_2} $$ (3) 式中：K1为红外热像仪的系统增益常数；K2为红外热像仪的补偿增益常数。
对于设定发射率与输出温度之间的关系，红外热像仪测温采用了斯蒂芬-玻耳兹曼定律进行描述。根据该定律：
$$ T = \sqrt[n]{{\frac{E}{{\varepsilon \sigma }}}} $$ (4) 式中：E为单位面积的辐射能量；ε为发射率；σ=5.67×10−8 W/（m2·K4）为斯蒂芬-玻耳兹曼常数；T为表面温度；n值与热像仪使用的波段有关。实验所用红外热像仪采用7.5~14 μm波段进行测量，此时n≈4。
可见观测距离通过角场影响输出电压，进而影响输出温度，最终对设定发射率产生影响。
最后，在实际观测过程中，很难保证红外热像仪在测温时正好垂直于观测表面，从而引起观测距离的变化和由于漫反射引起的热像仪接收能量的变化[27]。
因此，在本次析因实验中，选取温度T、表面粗糙度Ra、观测距离l和观测角度α作为实验参数，每个参数取高低两个水平，列于表3中。实验装置、实验材料都与测温实验相同。实验中，采用热电偶监测试件的加热温度，保温后采用红外热像仪对加热试件进行测温。当红外热像仪的测量温度与监测温度一致时，输入的发射率即为被测试件的设定发射率。
表 3 析因实验参数
Table 3. Factorial experiment parameters
Factor Level α/(°) 0 45 Ra/μm 0.4 1.8 l/mm 250 1500 T/℃ 100 500 -
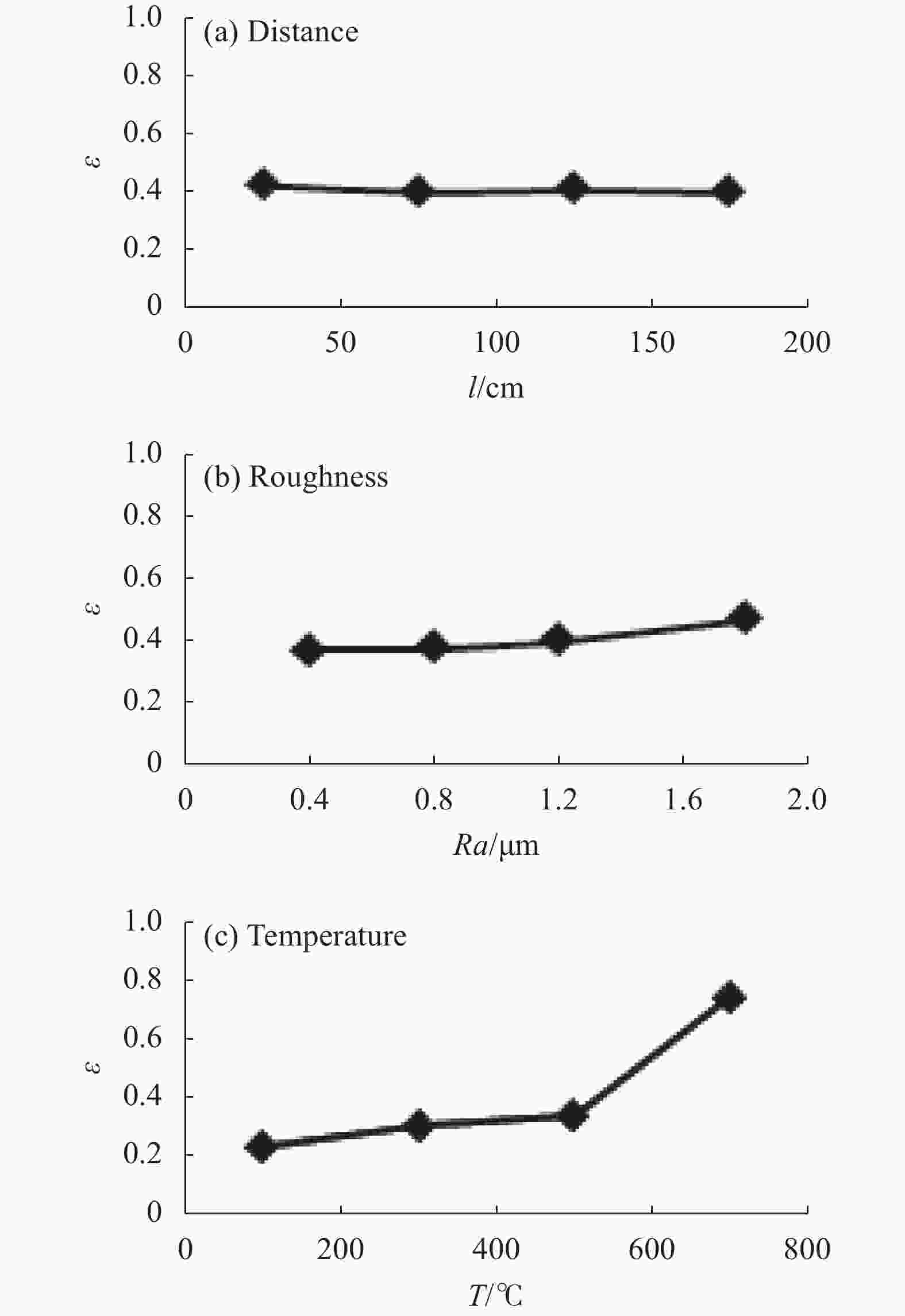
析因实验结果如图6所示。可以看出：温度、观测距离和表面粗糙度的改变都会影响设定发射率，而在[0°, 45°]范围内，观测角度对设定发射率几乎没有影响。设定发射率随着温度以及表面粗糙度的升高而增大，随着观测距离的增加而减小。
图 6 发射率的变化
Figure 6. Variation of emissivity
-
对SiCp/Al颗粒增强复合材料进行正交实验，进一步分析表面粗糙度、观测距离与温度对设定发射率的影响程度，并给出设定发射率修正经验公式。实验装置、实验材料以及设定发射率确定方法与析因实验相同。表4为正交实验的因素水平表。
表 4 正交实验因素水平表
Table 4. Orthogonal experimental factors and levels
Factor Level Ra/μm 0.4 0.8 1.2 1.6 l/mm 250 750 1250 1500 T/℃ 100 300 500 700 -
首先对实验结果进行极差分析。设Tjk表示第j个因素的第k个水平的实验指标之和，则极差Rj可作如下定义：
$$ {R_j} = \mathop {\max }\limits_{1 \leqslant k \leqslant 3} \left\{ {{T_{jk}}} \right\} - \mathop {\min }\limits_{1 \leqslant k \leqslant 3} \left\{ {{T_{jk}}} \right\}{\kern 1pt} (j = 1,2,3{\kern 1pt} \;k = 1,2,3,4) $$ (5) 结果列于表5中，表明温度对设定发射率的影响最大，表面粗糙度的影响次之，观测距离的影响最小。
表 5 极差分析
Table 5. Range analysis
Factor Rj Patch Ra/μm 0.1050 2 l/mm 0.0275 3 T/℃ 0.5175 1 图7为设定发射率均值的主响应图。可以看出：设定发射率随着温度的升高而增大，表面粗糙度的增大使得设定发射率增大，而测量距离的增大使得测定发射率稍有减小。
图 7 发射率均值的主响应图
Figure 7. Main response of the set emissivity
为进一步确定上述因素对发射率的影响程度，需要对试验结果进行方差分析。具体为计算实验结果的偏差平方和Q、自由度以及F分布值。通过数据分析软件Minitab对实验结果进行方差分析，结果列于表6中。其中，通过F值来确定各因素对设定发射率影响的显著性，即：
$$ F_{i}\sim F_{\alpha } (n\text{，}m) $$ (6) 式中：n为自由度；m为误差自由度；α为显著因子，这里分别取α=0.05、0.01。Fα的值由F分布表查得。
当Fi>F0.05(Fi, Fe)时，影响显著，当Fi>F0.01(Fi, Fe)时，影响高度显著，当Fi<F0.05(Fi，Fe)时，影响不显著。查表得到F0.05(3, 6)=4.76、F0.01(3, 6)=9.78。Ft>F0.01(3, 6)，Fl<F0.05(3, 6)，Ff<F0.05(3, 6)。其中，i=1, 2, 3… ，Ft为温度T的F值，Fl为距离l的F值，Ff为表面粗糙度Ra的F值。说明测量温度对发射率的影响呈现出高度显著性，而表面粗糙度和观测距离对发射率的影响不显著。
表 6 方差分析
Table 6. Analysis of variance
Factor Q n m F Ra/μm 0.235 3 6 4.64 l/mm 0.239 3 6 0.32 T/℃ 0.058 3 6 112.06 -
根据正交实验结果，采用多项式对发射率进行经验公式拟合，首先建立多项式回归方程：
$$ \begin{split} \varepsilon =& K + {a_0}R{a^3} + {a_1}R{a^2} + {a_2}Ra + {b_0}{l^3} + {b_1}{l^2} \hfill+ \\ & {b_2}l + {c_0}{T^3} + {c_1}{T^2} + {c_2}T \hfill \end{split} $$ (7) 式中：
$ \varepsilon $ 为材料的发射率，$ K $ 为常数；Ra为表面粗糙度；$ l $ 为观测距离；$ T $ 为温度。令
$ y = \varepsilon $ ，$ d = K $ ，$ {x_1} = Ra $ ，$ {x_2} = l $ ，$ {x_3} = T $ ，则回归方程变成：$$ \begin{split} y = &d + {a_0}{x_1}^3 + {a_1}{x_1}^2 + {a_2}{x_1} + {b_0}{x_2}^3 + {b_1}{x_2}^2 \hfill+ \\ & {b_2}{x_2} + {c_0}{x_3}^3 + {c_1}{x_3}^2 + {c_2}{x_3} \hfill \end{split} $$ (8) 自变量分别为x1、x2、x3，实验结果为y。正交试验共有16组，第i组的自变量为x1i、x2i、x3i，试验结果为yi，i=1，2，···，16。建立多元回归线性方程组：
$$ \left\{ \begin{split} {y_1}=& {a_{01}}{x_1}^3 + {a_{11}}{x_1}^2 + {a_{21}}{x_1} + {b_{01}}{x_2}^3 + \hfill \\ & {b_{11}}{x_2}^2 + {b_{21}}{x_2} + {c_{01}}{x_3}^3 + {c_{11}}{x_3}^2 + {c_{21}}{x_3} \hfill \\ & \begin{array}{*{20}{c}} {...} \end{array} \hfill \\ {y_{16}} =& d + {a_{016}}{x_1}^3 + {a_{116}}{x_1}^2 + {a_{216}}{x_1} + {b_{016}}{x_2}^3 + \\ & {b_{116}}{x_2}^2 + {b_{216}}{x_2} + {c_{016}}{x_3}^3 + {c_{116}}{x_3}^2 + {c_{216}}{x_3} \hfill \\ \end{split} \right. $$ (9) 用矩阵表示为：Y=Xα，其中：
$$ Y = \left\{ \begin{gathered} {y_1} \hfill \\ ... \hfill \\ {y_{16}} \hfill \\ \end{gathered} \right\} $$ $$ X = \left\{ {\begin{array}{*{20}{c}} 1&{{x_{11}}^3}&{{x_{11}}^2}&{{x_{11}}}&{...}&{{x_{31}}^3}&{{x_{31}}^2}&{{x_{31}}} \\ {}&{}&{}&{}&{...}&{}&{}&{} \\ 1&{{x_{116}}^3}&{{x_{116}}^2}&{{x_{116}}}&{...}&{{x_{316}}^3}&{{x_{316}}^2}&{{x_{316}}} \end{array}} \right. \text{，} $$ (10) $$ \alpha = {\left\{ {\begin{array}{*{20}{c}} d&{{a_0}}&{{a_1}}&{{a_2}}&{{b_0}}&{{b_1}}&{{b_2}}&{{c_0}}&{{c_1}}&{{c_2}} \end{array}} \right\}^{\rm{T}}} $$ 将实验数据代入矩阵得出α，得到SiCp/Al复合材料的设定发射率回归模型：
$$ \begin{split} \varepsilon =& 0.080\;6 + 513.5R{a^2} - 3.814Ra- \hfill \\ & 1.107 \times {10^{ - 10}}{l^3} + 3.14 \times {10^{ - 7}}{l^2} - 2.741 \times {10^{ - 4}}l+ \hfill \\ & 8.75 \times {10^{ - 9}}{T^3} - 8.406 \times {10^{ - 6}}{T^2} + 2.6 \times {10^{ - 3}}T \hfill \end{split} $$ (11) 采用F检验判断回归模型的显著性。计算总的偏差平方和SSt、残差平方和SSe以及回归平方和SSr[28-29]：
$$ \left\{ \begin{gathered} S {S_{\rm{t}}} = \sum\limits_{i = 1}^n {{{({y_i} - \bar y)}^2}} \hfill \\ S {S_{\rm{e}}} = \sum\limits_{i = 1}^n {{{({y_i} - {{\hat y}_i})}^2}} \hfill \\ S {S_{\rm{r}}} = \sum\limits_{i = 1}^n {{{({{\hat y}_i} - \bar y)}^2} = S{S_{{{\rm{t}}}}} - S{S_{\rm{e}}}} \hfill \\ \end{gathered} \right. $$ (12) 式中：
$ {\hat y_i} $ 为估计值；$ {y_i} $ 为测量值；$ \bar y $ 为测量的平均值。因变量总自由度dft，可分为残差自由度dfe和回归由度dfr两部分，则各部分自由度可表示为：
$$ {\rm{d}}{f_{\rm{t}}} = {\rm{d}}{f_{\rm{r}}} + {\rm{d}}{f_{\rm{e}}} $$ (13) 式中：dft=n−1；dfe=n−p−1；dfr=p，其中，实验组数n=16，变量个数p=3。
假设H0: β1=0，β2=0，β3=0。当原假设为真时，采用检验统计量为：
$$ F = \frac{{{{S {S_{\rm{r}}}} \mathord{\left/ {\vphantom {{S {S_{\rm{r}}}} P}} \right. } P}}}{{{{S {S_{\rm{e}}}} \mathord{\left/ {\vphantom {{S {S_{\rm{e}}}} {(n - p - 1)}}} \right. } {(n - p - 1)}}}} \sim F(p,n - p - 1) $$ (14) 取显著因子α=0.05，查阅F分布表可得到临界值F0.05(3,12)=3.49，将估计值与测量值代入公式(12)~(14)中，得到：F(3,12)=242.62。F(3,12)>F0.05(3,12)，可见该经验公式显著。
下面对公式的相关系数进行计算。根据公式(15)可得相关系数r：
$$ r = \sqrt {1 - \frac{{\displaystyle\sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} }}{{\displaystyle\sum\limits_{i = 1}^n {{{\left( {{y_i} - \bar y} \right)}^2}} }}} $$ (15) 式中：
$ {y_i} $ 为测量值；$ \bar y $ 为平均值，$ {\hat y_i} $ 为拟合值。将实验结果和预测结果代入，得到r=0.9915。表明实验结果和预测结果之间的相关程度很高，可以认为线性方程具有很好的可信度。
为进一步验证经验公式的准确性，采用实验结果对经验公式进行验证。在试验参数范围内取三组数据，采用给出的经验公式进行设定发射率修正，与实验方法确定的设定发射率进行比较并给出误差。实验条件、实验设备以及发射率的获取方法与以上实验完全相同。结果列于表7中。可见，经验公式计算结果的最大误差为2.76%，在可接受的范围内，证明文中给出的经验公式有效。
表 7 实验验证结果
Table 7. Experimental verification results
Ra
/μml
/mmT
/℃Measured value Calculated value Deviation 0.4 250 200 0.29 0.282 2.76% 0.4 250 400 0.29 0.283 2.76% 0.4 250 700 0.74 0.73 1.35% 分别采用设定发射率的测量值和经验公式计算值进行SiCp/Al复合材料温度测量并比较结果，如表8所示。可以看出：两种发射率测温结果相差不大，最大误差为2.33%，进一步证明拟合得到的SiCp/Al复合材料设定发射率经验公式具有较好的精度。
表 8 测温结果比较
Table 8. Comparison of temperature measurement results
Ra/
μml/
mmT/
℃Set emissivity
temperature/℃Formula predicted
value/℃Deviation 0.4 250 200 200.59 205.08 2.24% 0.4 250 400 403.03 412.43 2.33% 0.4 250 700 707.5 714.26 0.96% -
以热电偶法为代表的直接接触测温方法结果较为可靠，但也有不足。例如，自然热电偶法只能得到区域内的平均温度。人工热电偶法只能测量某一点的温度。另外，热电偶测温时的响应速度低，不能对瞬态温度进行测量；其他如氧化颜色比较法只能在材料氧化时才能使用，而且误差很大，只能用于粗略估计。红外热像仪可以实时观测物体表面的温度分布，同时响应速度快，目前，已经成为切削温度测量的主要方法之一。
由设定发射率对温度测量影响的实验结果可知，SiCp/Al复合材料的设定发射率在500 ℃时产生了突变。在常用的切削用量条件下，SiCp/Al复合材料的切削温度达400~1000 ℃甚至更高。因此，若使用红外热像仪进行SiCp/Al复合材料切削温度的测量，为保证切削温度的准确性，必须根据测量温度的范围进行设定发射率的修正。
为验证所得经验公式在切削测温中的适用性，进行切削实验，对SiCp/Al复合材料发射率在经验公式修正前和修正后所测得的切削温度进行对比分析。选取5组切削速度，设定测量距离为1 m，采用公式(11)对发射率进行修正。分别用修正前发射率和修正后发射率测量切削温度，实验设计如表9所示。
表 9 切削实验设计
Table 9. Cutting experiment design
v
/m·min−1l
/mmRa
/μmOriginal setting emissivity Original temperature
/℃1 40 1000 0. 63 0.3 223.18 2 80 1000 0. 536 0.3 356.7 3 120 1000 0. 501 0.3 446.3 4 160 1000 0. 53 0.3 313.64 5 200 1000 0. 567 0.3 429.8 表10为发射率修正前后切削温度对比。结果显示：发射率修正前后测量温度产生的偏差均值为9.38%，由此看出采用修正发射率能够有效的提高切削温度测量的准确性。
表 10 设定发射率修正前后切削温度对比
Table 10. Comparison of cutting temperature before and after setting emissivity correction
Setting emissivity Temperature /℃ Deviation Original Corrected Original Corrected 0.3 0.266445 223.18 244.6 9.597634% 0.3 0.262906 356.7 391.5 9.756098% 0.3 0.2719 446.3 478.7 7.259691% 0.3 0.266453 313.64 346.1 10.34945% 0.3 0.267178 429.8 472.7 9.981387% 对于其他材料切削温度的红外热像仪测量也必然同样存在设定发射率修正的问题。文中提出的设定发射率标定过程具有通用性。具体思路是：通过采用热电偶和红外热像仪对试件同时进行测温，以热电偶测量结果为基准，反复调整红外热像仪设定发射率，以红外热像仪输出温度与热电偶测量结果相同时的发射率输入值作为修正后的设定发射率，具体流程如图8所示。经验公式获取的过程为：首先通过单因素实验确定发射率的影响因素，其次通过正交实验获得设定发射率的经验公式，实现对设定发射率的修正。
图 8 红外热像仪设定发射率修正流程
Figure 8. Correction flow of the emissivity seting of infrared thermal imager
采用文中方法进行精确测温时，由于观测距离和表面粗糙度固定，因此只要获得设定发射率随温度的变化即可。在实际测量时，首先根据预估温度范围给定初始设定发射率进行测量。测量后采用该红外热像仪专用数据处理软件fluke-smartview进行温度输出。根据输出温度和设定发射率经验公式获得一个设定发射率修正值。然后采用该设定发射率的修正值获得修正温度输出。若该修正温度输出与前一次温度输出的差值大于给定误差限，则微调设定发射率重复上述过程。直到相邻两次温度输出的差值小于给定误差限，迭代过程完成，输出设定发生率和温度。文中方法通过设定发射率修正避免了设定发射率随测量温度范围、观测距离和表面粗糙度变化而带来的测量误差，提高温度测量的准确性。
但需要说明的是红外热像仪作为一种常用的非接触测温方法，只能测量物体的表面温度。随着有限元模拟技术的进步，采用有限元模型进行切削仿真已经成为一种常用方法。通过有限元仿真可以得到全场温度分布，但有限元模型的有效性需要通过实验结果进行验证。因此结合有限元模拟和红外测温法进行切削温度研究将是可行的研究方向之一。
-
文中结合热电偶，通过试验研究了采用红外热像仪进行切削温度测量时设定发射率的影响因素，并拟合了SiCp/Al复合材料设定发射率修正公式。主要结论如下：
(1)当被测温度较低时，采用目标材料推荐发射率的中间值作为设定发射率即可获得较为精确的测温结果，但当被测温度较高时，采用这种设定方法则会产生很大误差。对于SiCp/Al颗粒增强复合材料，测量温度小于500 ℃时，采用推荐发射率中值0.3可以获得较为准确的测量结果，但是当温度高于500 ℃时，采用这种发射率测定方法会产生较大的误差，必须进行修正。
(2)温度、表面粗糙度以及观测距离对设定发射率有影响，其中温度对物体发射率的影响最显著，表面粗糙度的影响次之，观测距离的影响最小。在[0°，45°]内测量角度对发射率几乎无影响。
(3)发射率随着温度的升高而增大，随着表面粗糙度的增大而增大，随着观测距离的增加而减小。采用多项式拟合可以获得精度较高的SiCp/Al复合材料设定发射率经验公式，设定发射率预测结果的最大误差为2.76%。
(4)文中给出了在切削温度测量这种高温测量时，为保证红外热像仪测量结果的准确性，被测试件设定发射率的确定方法，具有一定的通用性，可以用于进行其他材料红外测温时设定发射率的确定。
Experimental study on emissivity setting before precise temperature measurement of SiCp/Al cutting by infrared thermal imager
-
摘要: 发射率设定对红外热像仪测量结果的准确性具有决定性的影响，必须在测温前进行准确标定。首先通过热电偶标定试验研究了发射率设定对红外热像仪测温精度的影响。其次通过析因实验分析了设定发射率的影响因素。最后通过正交实验研究了各因素对设定发射率的影响程度，并进行了经验公式拟合和实验验证。结果表明：对于SiCp/Al复合材料，设定发射率在被测温度500 ℃前后有很大的差异，被测温度超过500 ℃时，采用推荐值作为设定方法则会产生较大误差。在[0°，45°]范围内测量角度对设定发射率几乎没有影响，但温度、表面粗糙度和观测距离都会影响设定发射率。多项式拟合获得的设定发射率经验公式预测结果的最大误差为2.76%。Abstract: Emissivity setting has a decisive impact on the accuracy of the measurement results of infrared thermal imager, so it must be calibrated accurately before temperature measurement. In this paper, the influence of emissivity setting on temperature measurement accuracy of infrared thermal imager was studied through thermocouple calibration test. Secondly, the influence factors of emissivity setting were analyzed by factorial experiment. Finally, the influence degree of each factor on the emissivity setting was studied by orthogonal experiment, and the empirical formula fitting and experimental verification were carried out. The results show that: for SiCp/Al composites, the emissivity setting is very different before and after the measured temperature is 500 ℃. When the measured temperature exceeds 500 ℃, using the recommended value as the setting method will produce large errors. In the range of 0°-45°, the measurement angle has no influence on the emissivity setting. However, temperature, surface roughness and observation distance all affect the emissivity setting. The maximum error of the empirical formula of the emissivity setting obtained by polynomial fitting is 2.76%.
-
Key words:
- cutting temperature /
- infrared thermal imager /
- emissivity setting /
- impacts /
- empirical formula
-
图 2 发射率为0.3时测量温度与实际温度的差异
Figure 2. Difference between measured and actual temperature when the emissivity is 0.3
图 4 不同发射率设定对测量温度的影响
Figure 4. Effect of different emissivities on the measured temperature
图 5 角场w与测量距离d的几何关系[21]
Figure 5. Geometric relationship between angle field w and measurement distance d
图 8 红外热像仪设定发射率修正流程
Figure 8. Correction flow of the emissivity seting of infrared thermal imager
表 1 Fluke-Ti640红外热像仪的主要技术参数
Table 1. Main technical parameters of fluke-Ti640 infrared thermal imager
Project Content Wavelength/µm 7.5−14 Frame rate/Hz 60 Temperature range/℃ −40 − +1200 Accuracy/℃ ±0.1 
下载: 导出CSV
表 2 SiCp/Al复合材料基本性能
Table 2. Basic properties of SiCp/Al composite
Parameter 2024Al SiC Thermal conductivity/(W·m−1·K−1） 180 81 Specific heat capacity/(J·kg−1·K−1） 880 427 Volume fraction 55% 45% Density/(kg·m−3) 2.7×103 3.13×103 Poisson ratio 0.34 0.14 Thermal expansion coefficient/K−1 23.6×10−6 4.9×10−6
下载: 导出CSV
表 3 析因实验参数
Table 3. Factorial experiment parameters
Factor Level α/(°) 0 45 Ra/μm 0.4 1.8 l/mm 250 1500 T/℃ 100 500
下载: 导出CSV
表 4 正交实验因素水平表
Table 4. Orthogonal experimental factors and levels
Factor Level Ra/μm 0.4 0.8 1.2 1.6 l/mm 250 750 1250 1500 T/℃ 100 300 500 700
下载: 导出CSV
表 6 方差分析
Table 6. Analysis of variance
Factor Q n m F Ra/μm 0.235 3 6 4.64 l/mm 0.239 3 6 0.32 T/℃ 0.058 3 6 112.06
下载: 导出CSV
表 7 实验验证结果
Table 7. Experimental verification results
Ra
/μml
/mmT
/℃Measured value Calculated value Deviation 0.4 250 200 0.29 0.282 2.76% 0.4 250 400 0.29 0.283 2.76% 0.4 250 700 0.74 0.73 1.35%
下载: 导出CSV
表 8 测温结果比较
Table 8. Comparison of temperature measurement results
Ra/
μml/
mmT/
℃Set emissivity
temperature/℃Formula predicted
value/℃Deviation 0.4 250 200 200.59 205.08 2.24% 0.4 250 400 403.03 412.43 2.33% 0.4 250 700 707.5 714.26 0.96%
下载: 导出CSV
表 9 切削实验设计
Table 9. Cutting experiment design
v
/m·min−1l
/mmRa
/μmOriginal setting emissivity Original temperature
/℃1 40 1000 0. 63 0.3 223.18 2 80 1000 0. 536 0.3 356.7 3 120 1000 0. 501 0.3 446.3 4 160 1000 0. 53 0.3 313.64 5 200 1000 0. 567 0.3 429.8
下载: 导出CSV
表 10 设定发射率修正前后切削温度对比
Table 10. Comparison of cutting temperature before and after setting emissivity correction
Setting emissivity Temperature /℃ Deviation Original Corrected Original Corrected 0.3 0.266445 223.18 244.6 9.597634% 0.3 0.262906 356.7 391.5 9.756098% 0.3 0.2719 446.3 478.7 7.259691% 0.3 0.266453 313.64 346.1 10.34945% 0.3 0.267178 429.8 472.7 9.981387%
下载: 导出CSV
-
[1] Sheng Jing, Chiu Yijui. Lin Bingjing Determination of a coupling equation for milling parameters based on optimal cutting temperature [J]. The International Journal of Advanced Manufacturing Technology, 2018, 98(1-4): 129-141. [2] Ge Yingfei, Xu Jiuhua, Fu Yucan. Cutting temperature investigation when high-speed milling of SiCP/Al composites [J]. Materials Science Forum, 2011, 697-698: 198-203. doi: 10.4028/www.scientific.net/MSF.697-698.198 [3] Piotr Zgórniak, Wojciech Stachurski, Dariusz Ostrowski. Application of thermographic measurements for the determination of the impact of selected cutting parameters on the temperature in the workpiece during milling process [J]. Journal of Mechanical Engineering, 2016, 62(11): 657-664. [4] Ch Sateesh Kumar, Saroj Kumar patel, Anshuman Das. Experimental and numerical investigations on the temperature distribution in PVD AlTiN coated and uncoated Al2O3/TiCN mixed ceramic cutting tools in hard turning of AISI 52100 steel [J]. IOP Conference Series: Materials Science and Engineering, 2018, 338(1): 012021. [5] Li Hongyun, Sun Xiaogang, Yuan Guibin. Accurate measuring temperature with infrared thermal imager [J]. Optics and Precision Engineering, 2007, 15(9): 1366-1341. (in Chinese) [6] Lane B, Whitenton E, Madhavan V, et al. Uncertainty of temperature measurements by infrared thermography for metal cutting applications [J]. Metrologia, 2013, 50(6): 637-653. doi: 10.1088/0026-1394/50/6/637 [7] Ke Veina, Zhu Daoqiang, Cai Guoqiang. Simulation and analysis of spectral emissivity of/ metal [J]. Acta aeronautica et Astronautica Sinica, 2010, 31(11): 2139-2145. (in Chinese) [8] Shi Deheng, Liu Qionglan, Zhu Zunlue, et al. Experimental study of the relationships between the spectral emissivity of brass and the temperature in the oxidizing environment [J]. Infrared Physics and Technology, 2014, 64: 119-124. doi: 10.1016/j.infrared.2014.03.001 [9] Shi Deheng, Liu Qionglan, Zhu Zunlue, et al. Study on relationships between the spectral emissivity of DC01 steel and temperature in an oxidizing environment [J]. International Journal of Thermophysics, 2014, 35: 1545-1556. doi: 10.1007/s10765-014-1709-y [10] Wang Peng, Xie Zhi, Meng Hongji, et al. Effects of the temperature and roughness on the metal emissivity[C]//27th Chinese Control and Decision Conference, 2015: 3206-3209. [11] HangJin Jo, King Jonathan L, Kyle Blomstr, et al. Spectral emissivity of oxidized and roughened metal surfaces [J]. International Journal of Heat and Mass Transfer, 2017, 115: 1065-1071. doi: 10.1016/j.ijheatmasstransfer.2017.08.103 [12] Shen Jiuli, Zhang Yucun, Xing Tingting. The study on the measurement accuracy of non-steady state temperature field under different emissivity using infrared thermal image [J]. Infrared Physics and Technology, 2018, 94: 207-213. doi: 10.1016/j.infrared.2018.09.022 [13] Hartsfield T M, Iverson A J , Baldwin J K. Reflectance determination of optical spectral emissivity of metal surfaces at ambient conditions [J]. Journal of Applied Physics, 2018, 124: 105107. doi: 10.1063/1.5042601 [14] Zhao Wanmeng, Li Longfei, Yuan Zeye, et al. Direction spectral emissivity of Ti6Al4V alloy [J]. Acta Optica Sinica, 2020, 40(8): 0830002. (in Chinese) [15] Jean Pierre Monchau, Mario Marchetti, Laurent Ibos, et al. Emissivity measurements of building and civil engineering materials: A new device for measuring emissivity [J]. International Journal of Thermophysics, 2014, 35: 1817-1831. doi: 10.1007/s10765-013-1442-y [16] Ibos L, Marchetti M, Boudenne A, et al. Infrared emissivity measurement device: principle and applications [J]. Measurement Science & Technology, 2006, 17: 2950-2956. [17] Liu Yufang, Hu Zhili, Shi Deheng, et al. Experimental investigation of emissivity of steel [J]. International Journal of Thermophysics, 2013, 34(3): 496-503. doi: 10.1007/s10765-013-1421-3 [18] Zhang Min, Yang Guang, Zhang Li, et al. Application of ZrB2 thin film as a low emissivity filmat high temperature [J]. Applied Surface Science, 2020, 527: 146763. doi: 10.1016/j.apsusc.2020.146763 [19] Bai Jingchen, Yu Qingbo, Hu Xianzhong, et al. Surface emissivity measurement technique based on infrared thermal imager [J]. Journal of Northeastern University (Natural Science), 2013, 34(12): 1747-1750. (in Chinese) [20] Wang Zhingren, Li Dongyang, Ruan Banchao, et al. Experimental research on the measurement emissivity for metal reflective surface [J]. Machinery Design & Manufacture, 2016(6): 226-228. (in Chinese) [21] Zhang Yucun, Chen Yiming, Fu Xianbin, et al. A method for reducing the influence of measuring distance on infrared thermal imager temperature measurement accuracy [J]. Applied Thermal Engineering, 2016, 100: 1095-1101. doi: 10.1016/j.applthermaleng.2016.02.119 [22] Li Wenjun, Xu Yongda, Zheng Yongjun. Match method of emissivity measurement based on infrared thermal imager and surface thermometer [J]. China Measurement & Test, 2017, 43(6): 12-15. (in Chinese) [23] Liao Panpan, Zhang Jiamin. Research on influence factors for measuring and method of correction in infrared thermometer [J]. Infrared Technology, 2017, 39(2): 173-177. (in Chinese) [24] Xiao Binan, Gong Lliehang, Zeng Rui. Analysis and simulation of metallic infrared emissivity [J]. Infrared Technology, 2008,30(6): 358-360. (in Chinese) [25] Yu Kun, Liu Yufang, Jia Guangrui, et al. Analysis on factors affecting the infrared spectral emissivity of steel surface [J]. Infrared Technology, 2011, 33(5): 289-292. (in Chinese) [26] Pan Yawen. Experimental investigation of effect material emissivity elements[D]. Xinxiang: Graduate School of Henan Normal University, 2013. (in Chinese) [27] Evgeniy Petukhov, Mariya Romodanovskaya. The temperature measurements in the formation zone during high-pressure jet cutting [J]. Materials Today:Proceedings, 2019, 19: 2471-2474. doi: 10.1016/j.matpr.2019.08.111 [28] Degroot M H. Probability and Statistics[M]. New York: Addison-Wesley, 1975. [29] Bickel P J, Doksum K A. Mathematical Statistics[M]. New York: Chapman and Hall/CRC, 1977. -
点击查看大图
计量
- 文章访问数: 91
- HTML全文浏览量: 17
- PDF下载量: 25
- 被引次数: 0
