-
图像拼接是指将数张具有重叠部分的图像进行拼接的过程。图像拼接流程大致分为以下几个步骤,分别是:特征提取、图像配准、图像对齐。图像特征的提取是图像拼接中最重要的一个环节,Lowe[1]提出的SIFT尺度不变特征变换(Scale-Invariant Feature Transform, SIFT)提取算法,其具有尺度不变性和旋转不变性。Bay等人[2]提出的SURF (Speeded-Up Robust Feature)算法,速度相比SIFT提升3倍左右,性能并没有下降。图像配准是图像拼接中关键的一环,通常利用全局或者局部参数对图像进行变换来对齐图像。边佳旺等人[3]提出一种基于网格运动统计的GMS算法能够在低质量以及模糊的图像中实现实时的匹配,目前已经广泛使用。
远红外图像分辨率低、对比度低、信噪比低,存在重复结构和稀疏机构,并且纹理和边缘特征较少。近年来,许多学者针对红外图像拼接进行研究。樊佩琦等人[4]提出了一种改进的SURF方法用于红外图像拼接。Alam等人[5]利用基于梯度的配准算法来估计所获取的红外图像帧之间的偏移。王彦辉等人[6]提出了一种灰度非均匀性校正算法来校正远红外图像序列的每一帧,然后提出基于SURF的配准方法来拼接校正后的图像序列。目前针对远红外图像拼接方法的主要研究对象是两个或少量远红外图像,不适合大批量远红外图像。
广视角的大批量远红外图像序列往往会带有视差,而在自然光图像拼接的研究中,处理视差的方法是采用局部变换的方式,将图像划分为多个网格,针对每一个网格单独建立计算参数的模型,来保证重叠区域的对齐。Zaragoza等[7]提出的APAP(AS-Projective-As-Possible)方法将图像划分为多个网格,并利用“Moving DLT”(Direct Linear Transformation)单独计算每个网格的局部单应性。APAP虽然被认为是一种高效扭曲变形图像来对齐重叠区域的方法,但是其非重叠区域往往会产生严重的图像畸变,尤其在大视差的场景下。Chang等人[8]提出SPHP (Shape-Preserving Half-Projective)方法将图像划分成三部分:重叠区域、过渡区域和非重叠区域,既保证重叠区域的局部对齐,又能尽可能少地产生畸变。Lin等人提出的AANAP(Adaptive-As-Natural-As-Possible)[9]方法结合局部单应性与全局相似变换,能够获取更加自然的结果。虽然以上方法在少量自然光图像的拼接中取得了很好的效果,但是无法解决大量图像拼接的问题,更无法解决大量远红外图像的序列拼接问题。
在获取大批量远红外图像时,由于直升机由上往下逐列地采集多组红外顺序图像序列,单组顺序图像序列图片较多,单列连续拼接会导致特征消失;而多组顺序图像序列拼接完成构成多列图像后,由于透视关系,会导致相邻序列图像之间上下重叠率不一致,难以配准。因此,大批量远红外图像的拼接更加依赖算法的精确性。
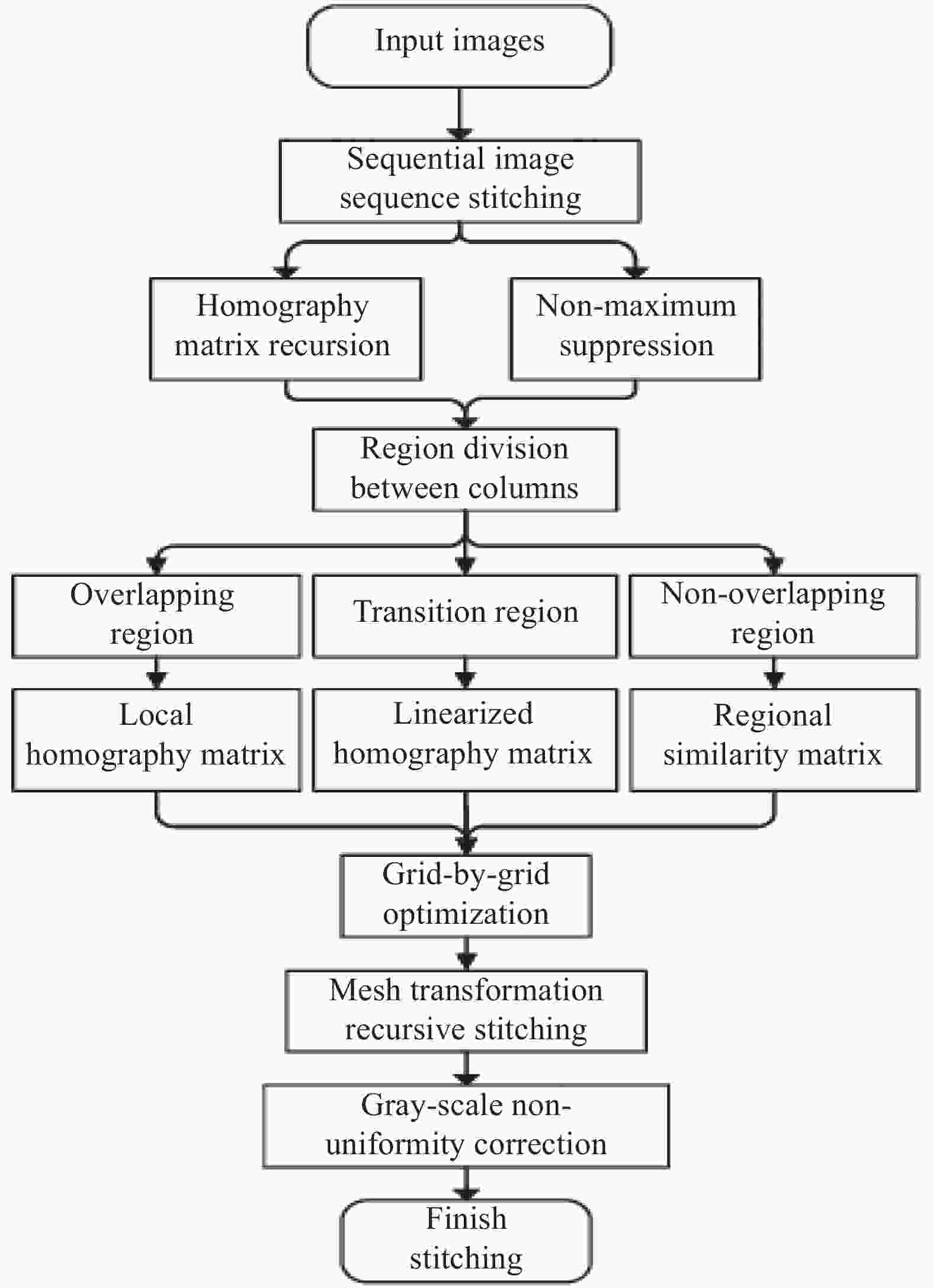
文中针对非一致重叠率大批量远红外图像的拼接问题,提出了一种由单列到列间的远红外图像拼接方法。在单列图像拼接阶段,基于非极大值抑制原理求取单应性矩阵,并推导传递关系以获得当前图像间的坐标关系进行单列顺序远红外图像的拼接。在列间图像拼接阶段,通过划分网格,结合区域相似变换和局部单应变换逐网格优化变换矩阵的权重,并通过网格变换的递推来实现列间远红外图像的拼接。最后,将文中提出的拼接方法与其他方法和主流软件的拼接效果进行对比与分析,证明了该方法的有效性。
-
文中实验中所使用的远红外图像序列是从直升机上获取的航拍图。红外热像仪可以自上而下旋转从
${\theta _1}$ ~${\theta _n}$ 的角度来逐列连续拍摄多张远红外图像。固定转轴拥有自动控制装置,能够确保每次旋转的角度是固定的,因此采集的每列图像中,相邻两张拥有同样的重叠率(图像重叠率定义为图像重叠面积与图像面积之比)。但是飞机在飞行过程中无法保持平稳飞行,可能存在升降或者抖动等情况;同时由于技术受限,固定转轴的自动控制装置的起始角度不是固定的,只能确保每列中相邻编号的两张图像是有重叠的,而不同列中的图像无法保证其相邻编号的两张图像是有重叠部分的。受限于该问题,文中采取的拼接方案是先拼接每一列中的所有图像,然后进行列之间的拼接。
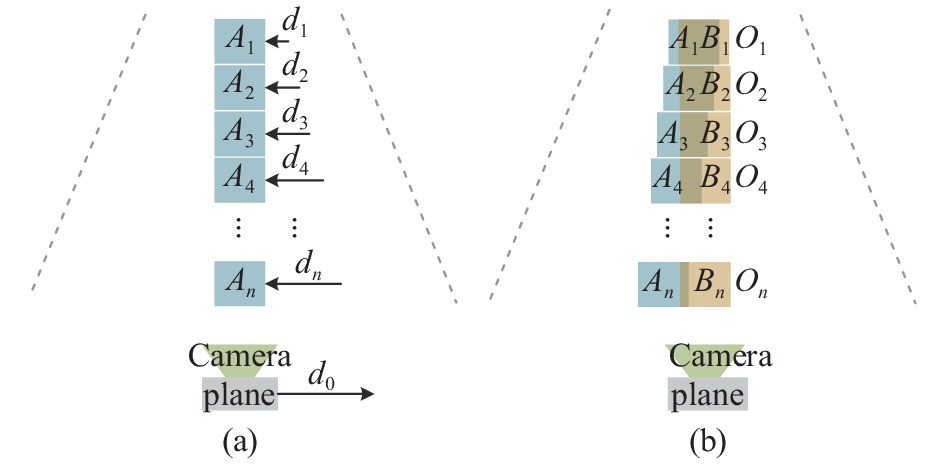
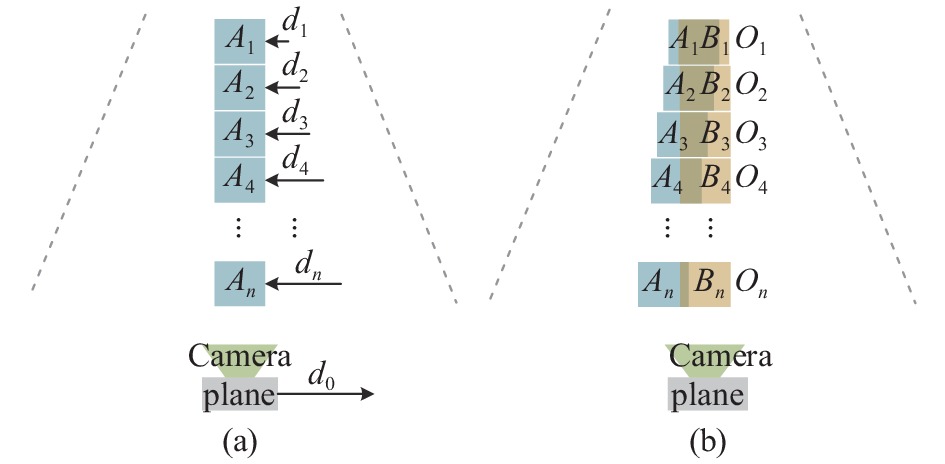
遵循透视的原理,三维空间通过相机在二维平面成像时,物体会符合近大远小的关系。航拍图像的拼接需要考虑透视问题,整个待取景平面符合近大远小的关系,但是相机在取景时其取景框的大小不变,取景不同距离的图像时,其取景框内的信息量是不一致的,图1(a)中
${A_1}$ ~${A_n}$ ,取景框中所容纳的信息量会减少。当飞机对当前列取景完后,位移一段距离${d_0}$ ,那么根据透视原理,所在${A_1}\sim{A_n}$ 的区域相对于取景框会分别位移${d_1} \sim {d_n}$ 的距离,且${d_1} < < {d_n}$ ,此时再次对下一列取景时会导致图1 (b)中所示的横向重叠率${O_1}$ ~${O_n}$ 不一致,造成单列图像之间存在由上到下重叠率不一致的现象,难以进行列与列之间的图像配准。 -
远红外图像对比度较低且特征信息较少,在单列图像拼接的过程中,若依照自然光图像的拼接方法,逐张计算单应性矩阵进行配准,非重叠区域在变换之后可能会出现扭曲与畸变,后续图像的拼接将出现有效特征点减少的问题。针对这个问题,文中提出一种充分利用原图像特征信息的多图拼接方法。
-
单应性递推即选取一张图像作为基准图像,后面每相邻两张图像彼此进行配准[10],被提取特征的图像没有经过任何几何变换,特征信息完整。获得相邻图像的变换矩阵后,将变换矩阵相乘来传递各图像的位置关系,最终可以令全部图像统一到基准图像的坐标系之中。
图像
${A_i}$ 中的某一坐标${P_{i,i}}{({x_{i,i}},{y_{i,i}},1)^{\rm {T}}}$ 经过单应性矩阵变换为${A_{i - 1}}$ 的坐标系中,其公式如下:$$ {P_{i,i - 1}}{\text{ = }}\left( {\begin{array}{*{20}{c}} {{x_{i,i - 1}}} \\ {{y_{i,i - 1}}} \\ 1 \end{array}} \right){\text{ = }}\left( {\begin{array}{*{20}{c}} {{h_1}}&{{h_2}}&{{h_3}} \\ {{h_4}}&{{h_5}}&{{h_6}} \\ {{h_7}}&{{h_8}}&{{h_9}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_{i,i}}} \\ {{y_{i,i}}} \\ 1 \end{array}} \right) = {H_{i - 1}}{P_{i,i}} $$ (1) 式中:矩阵
${H_{i - 1}}$ 是相邻图像${A_i}$ 以${A_{i{{ - }}1}}$ 的坐标系为基准坐标系进行投影变换的单应性矩阵;坐标${P_{i,i}}{({x_{i,i}},{y_{i,i}},1)^{\rm {T}}}$ 和${P_{i,i{{ - }}1}}{({x_{i,i{\text{ - }}1}},{y_{i,i{{ - }}1}},1)^{\rm {T}}}$ 分别是图像${A_i}$ 投影变换前后对应的一对齐次坐标。假设以第一张图像
${A_1}$ 作为基准图像,图像${A_i}$ 的任一坐标通过递推就可以变换到基准坐标下,公式如下:$$ {P_{i,1}} = \prod\limits_{k = 1}^{i - 1} {{H_k}{P_{i,i}}} $$ (2) 式中:坐标
${P_{i,i}}$ 和${P_{i,1}}$ 分别是图像${A_i}$ 投影变换到图像${A_1}$ 的基准坐标系前后对应的一对齐次坐标。${H_k}(k = 1,2,$ $\cdots ,i - 1)$ 分别为${P_{i,i}}$ 变换到${A_k}$ 坐标系下的单应性矩阵。因此,将${A_i}$ 图像变换到${A_1}$ 的基准坐标系的单应性矩阵$ H_i^c $ 可表示如下:$$ H_i^c = \prod\limits_{k = 2}^i {{H_k}} $$ (3) -
相比于自然光图像,航拍远红外图像的特征信息较少,常规的特征检测和特征匹配难以检测和匹配上所有的特征点。由于特征均匀分布能够实现更精细的拼接效果[11],因此文中创新性地运用非极大值抑制的方法:在特征提取过程中提高阈值来获取更多特征点。由于特征点往往密集出现,通过非极大值抑制(Non-Maximum Suppression, NMS)使得特征密集区域稀疏化。如图2左上角和左下角所示,由于检测器设置了更低的阈值,利用NMS进行过滤,保留最大响应的特征点,使得两幅图像中几乎拥有同样的特征点数量,但是特征分布在更多区域,并且更均匀。

图 2 特征均匀分布对对齐能力的影响对比图
Figure 2. Comparison of the effect of uniform distribution of features on alignment ability
除此之外,如图2左下角所示,非极大值抑制通过更低的阈值能够获取更多的特征信息,弥补远红外图像特征信息较少的缺点,并没有提高后续的计算量[12]。均匀分布的特征点利于后续计算局部单应性矩阵,其需要计算各特征点对于各局部单应变换的贡献,因此均匀分布的特征点会提供更准确的权重。
-
由于图1中所描述的重叠率不一致的问题,完成单列的拼接后,会出现如图3(a)中所示的列与列之间的配准问题。当RANSAC算法迭代拟合特征点集,筛选用来计算单应性矩阵的特征点时,不同的阈值会保留不同区域的特征点集,如图3(a)中
${{{F}}_1}$ ~${{{F}}_4}$ 特征点及其所在区域的特征点集。若阈值过低,则这些特征点集计算出的单应性矩阵难以代表全局的投影变换,在将图像透视投影后会出现部分像素点对齐而部分像素点未对齐的现象,如图3(b)、(c)所示;而阈值过高会导致重叠区域对齐时都存在部分误差。文中提出一种划分网格并逐网格优化,利用投影变换的递推关系来处理非一致重叠率的列间拼接问题。见图3(d),不再计算全局单应性,而是结合网格的局部单应性及区域相似变换,实现重叠区域的像素对齐的同时,确保非重叠区域不会产生图像畸变。局部单应性变换的递推关系能够实现非一致重叠率的多列图像拼接。 -
相似变换只做平移、旋转和等比例缩放的变换,它和保持欧式距离的刚体变换一样具有保角性。其点之间的距离不再保持不变,但距离比依旧保持不变。在图像的非重叠区域使用相似变换而非单应变换,就不会引入任何透视变形,能够有效减少畸变,使拼接的图像更加自然。相似变换的公式如下:
$$ \left( \begin{gathered} {x_q} \\ {y_q} \\ 1 \\ \end{gathered} \right) = S\left( {\begin{array}{*{20}{c}} {{x_p}} \\ {{y_p}} \\ 1 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {s\cos (\theta )}&{ - s\sin (\theta )}&{{t_x}} \\ {s\sin (\theta )}&{s\cos (\theta )}&{{t_y}} \\ 0&0&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_p}} \\ {{y_p}} \\ 1 \end{array}} \right) $$ (4) 式中:
$S$ 为相似矩阵;$\theta $ 为旋转角;$s$ 为缩放尺度;${t_x}$ 和${t_y}$ 为平移矢量;$({x}_{p},{y}_{p},1{)}^{\rm T}$ 和${({x}_{q},{y}_{q},1)}^{{\rm T}}$ 分别表示特征点坐标及其变换后的投影坐标。列图像是由很多图像拼接而成的,长宽比值较大,且多列图像间重叠率不一致。因此,直接通过所有特征点求取全局相似变换存在较大误差[13],文中通过RANSAC方法对特征点进行分组,按照分组对不同的区域分别计算区域相似矩阵。
-
通过全局单应变换会导致列与列之间的重叠区域难以对齐,因此文中考虑划分网格,利用局部单应变换来对齐重叠区域。APAP方法中将图像划分成多个网格,通过移动直接线性变换(Moving DLT)计算局部单应矩阵对不同网格内的坐标执行不同的单应变换,令重叠区域精准对齐。
两幅待拼接图像中可能存在几百上千对特征点。首先将图像划分成
$m$ 个网格,假设每个网格中存在$n$ 对特征点,通常使用最小二乘法使得累计平方和误差最小来估计各个网格的局部单应性矩阵${\hat h^{(k)}}$ ,如公式(5)所示:$$ \begin{split} & {{\hat h}^{(k)}} = \mathop {\arg \min }\limits_h \sum\limits_{i = 1}^n {{w_i}^{(k)}{{\left\| {{a_i}h} \right\|}^2}} {\text{ = }}\mathop {\arg \min }\limits_h {W^{(k)}}{\left\| {Ah} \right\|^2} \\ & {\rm s.t.}\;{\left\| h \right\|^2} = 1,k = 1,2, \cdots ,m \\[-2pt] \end{split} $$ (5) 利用高斯分布计算各特征点对各网格贡献的权重,高斯分布的密度函数如下:
$$ f(x) = \frac{1}{{\sigma \sqrt {2\pi } }}{{\rm e}^{ - \frac{{(x - \mu )^2}}{{2{\sigma ^2}}}}} $$ (6) 权重
${w_i}^{(k)}$ 的具体表达如下所示:$$ {w_i}^{(k)} = {{\rm e}^{ - ({{({x^{(k)}} - {x_i})}^2} + {{({x^{(k)}} - {x_i})}^2})/{\sigma ^2}}} $$ (7) 式中:
$({x^{(k)}},{y^{(k)}})$ 为第$k$ 个网格的中心坐标;$({x_i},{y_i})$ 为第$i$ 个特征点的坐标。公式(7)表明特征点越靠近网格中心则对当前网格的局部单应性贡献越大,但由于待拼接图像的边缘处的网格远离所有特征点,因此特征点贡献的权重趋近于0,会导致边缘出现波浪形畸变。APAP中提出使用一个阈值参数$\lambda $ 用来限制权重的最小值。文中创新性地提出更为简洁的柯西分布计算各特征点的贡献权重。柯西分布的密度函数如下:$$ f(x) = \frac{1}{{{\text{π}} \gamma [1 + {{\left( {\frac{{x - {x_0}}}{\gamma }} \right)}^2}]}} $$ (8) 所以改进的权重
${w_i}^{(k)'}$ 的计算方式如下所示:$$ {w_i}^{(k)'} = \frac{1}{{1 + \dfrac{{{{({x^{(k)}} - {x_i})}^2} + {{({x^{(k)}} - {x_i})}^2}}}{{{\gamma ^2}}}}} $$ (9) -
图像的重叠区域通过划分网格分别进行局部单应变换能够获取更加精细的对齐效果,但是局部单应变换外推到非重叠区域时,会产生极端和非自然的缩放效果,导致严重的透视失真。AANAP方法中在图像边界以等差距离构建锚点。它们属于不同的网格,有不同的局部单应性。利用泰勒级数前两项对锚点进行线性化,网格局部单应性矩阵的线性化则是利用线性化的锚点通过T分布加权获取。
文中提出从左至右逐渐将网格的变换由局部单应变换平滑地转换为区域相似变换。在重叠区域利用局部单应性变换实现像素的精确对齐;在非重叠区域利用区域相似变换避免产生图像畸变;而重叠和非重叠之间的过渡区域,则结合线性化的局部单应性变换、局部单应性变换以及区域相似变换,在拼接时实现更加自然的过渡,为此,给出各单元格的变换矩阵公式如下:
$$ \begin{split} &{{\hat H}^{(k)}} = {{{μ}} _1}{{\hat h}^{(k)}} + {{{μ}} _2}{{\hat h}_L}^{(k)} + \omega {S_i} \\ & {\rm s.t.}\;{{\mu} _1} + {{\mu} _2} + \omega = 1,\; k = 1,2,\cdots,m \\[-2pt] \end{split} $$ (10) 式中:
${h^{(k)}}$ 为公式(5)中求得的各网格的局部单应性矩阵;${h_L}^{(k)}$ 为加权线性化的局部单应性矩阵;${S_i}$ 为各区域的相似变换矩阵。设${\mu} {\text{ = }}{{\mu} _1}{\text{ + }}{{\mu} _2}$ ,其中${{\mu} _1}$ 和${{\mu} _2}$ 是局部单应性的线性部分和非线性部分所占权重;${\mu}$ 和$\omega $ 是局部单应性和区域相似度所占权重。求取权重${{\mu} _1}$ 、${{\mu} _2}$ 和$\omega $ 的公式如下:$$ \left\{ \begin{gathered} \omega = \frac{{\left| {({x^{(k)}} - {x_{\min }})({x_{\max }} - {x_{\min }}) + ({y^{(k)}} - {y_{\min }})({y_{\max }} - {y_{\min }})} \right|}}{{({x_{\max }} - {x_{\min }})({y_{\max }} - {y_{\min }})}} \\ {{\mu} _1} = 1 - \omega - {{\mu} _2} \\ {{\mu} _2} = \frac{{\left| {({x^{(k)}} - {x_i})({x_c} - {x_i}) + ({y^{(k)}} - {y_i})({y_c} - {y_i})} \right|}}{{({x_c} - {x_i})({y_c} - {y_i})}} \\ \end{gathered} \right. $$ (11) 式中:
$({x^{(k)}},{y^{(k)}})$ 是第$k$ 个单元格的中心坐标;$({x_{\min }},{y_{\min }})$ 、$({x_l},{y_l})$ 、$({x_r},{y_r})$ 、$({x_{rc}},{y_{rc}})$ 和$({x_{\max }},{y_{\max }})$ 分别是${K_{\min }}$ 、${K_l}$ 、${K_r}$ 、${K_{rc}}$ 和${K_{\max }}$ 的坐标,如图4(b)所示,一条直线$L$ 分别穿过基准图像${I_r}$ 的中心点${O_r}$ ,以及单应变换后的图像${{{I}}_{{t}}}$ 的中心点${O_t}$ ,得到以上四个坐标,其中${K_{\min }}$ ,${K_{\max }}$ 分别是拼接后图像的最左侧和最右侧,${K_{lc}}$ ,${K_{rc}}$ 分别是线段$ {\overline {{K_{\min }}K} _l} $ ,$ {\overline {{K_r}K} _{\max }} $ 的中点,${K_{lc}} \sim {K_l}$ ,${K_r} \sim {K_{rc}}$ 分别是过渡区域,${K_l} \sim {K_r}$ 是重叠区域。应当理解,从重叠区域到过渡区域,再向外渐变到非重叠区域,这些区域中的网格遵循局部单应变换权重大,过渡到线性加权的单应变换权重大,最后过渡到区域相似变换权重大,同一区域中不同单元格中三种变换的权重也是不一。综上可获取权重分布表,如表1所示。
表 1 单应性矩阵的权重分布表
Table 1. Weight distribution of homography matrix
Position of
grid kProportion of local
homography matrixProportion of linearizated local
homography matrixProportion of regional similarity
homography matrix${x_{\min }} < {x^{(k)}} < {x_{lc}}$ 0% 0% 100% ${x_{lc}} < {x^{(k)}} < {x_l}$ 0% -100% 0% - 100% 0% -100% ${x_l} < {x^{(k)}} < {x_r}$ 0% 100% 0% ${x_r} < {x^{(k)}} < {x_{rc}}$ 0% - 100% 0% - 100% 0% - 100% ${x_{rc}} < {x^{(k)}} < {x_{\max }}$ 0% 0% 100% -
由于直升机采集图像序列时存在图1中所示的非一致重叠率的问题,文中将单列图像划分为网格,并通过多种变换加权实现更精确的对齐结果,以及更自然的拼接效果。但是当两列图像的拼接扩展到多列图像的拼接时会出现问题。
如图5所示(为方便表述,此处用单张图像代替列间图像进行展示),采集图像的重叠率区间为(10%, 90%),跨度较大。若当前已完成
${I_1}$ 和${I_2}$ 图像的拼接,由于局部单应性权重占比大,因此${C_{21}}$ 区域的图像会有轻微扭曲,特征信息会有相应的变化,此时对${I_1}$ 和${I_2}$ 拼接完成的图像与${I_3}$ 进行拼接,由于${I_1}$ 、${I_2}$ 和${I_3}$ 的重叠区域存在交错,会导致部分匹配特征消失,影响图像对齐的结果。为了得到更平滑的拼接结果,前文将各个网格的变换矩阵由区域相似度矩阵、局部单应性矩阵以及线性化的局部单应性矩阵加权融合成而成[14],此处称之为网格变换,如图6(a)所示,当拼接A、B和C时,网格变换矩阵
$H_B^{(k)}$ 将B图像投影到A图像所在的基准坐标系下,网格变换矩阵$H_C^{(k)}$ 将C图像投影到B图像所在的基准坐标系下,如图6(b)所示。因此,$H_B^{(k)} \times $ $ H_C^{(k)}$ 将C图像投影到A图像所在的基准坐标系下,如图6(c)所示。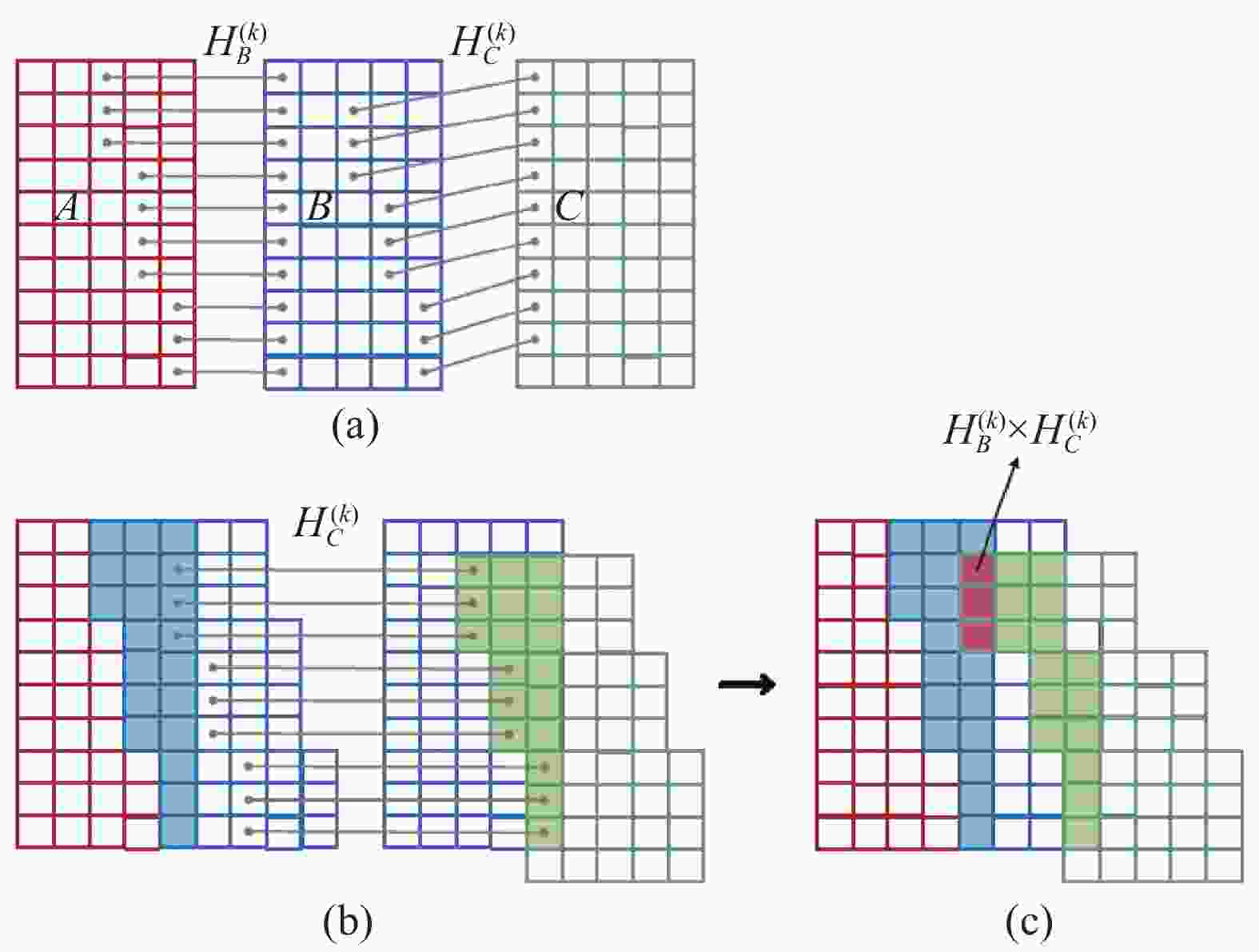
图 6 网格变换递推与列间拼接示意图
Figure 6. Schematic diagram of grid transformation recursion and inter column splicing
设有
$N$ 张拼接好的单列图像,${p_{i,k}}$ 是其中第$i$ 张图像的第$k$ 个网格中的某一坐标。$H_j^{(j,k)}$ 是第$j$ 张图像的第$k$ 个网格,经过网格变换投影到上一张图像坐标系的变换矩阵,则第$i$ 张图像的某一坐标投影到基准坐标系(假设第一张图像为基准图像)的坐标为${p_{i,k}}'$ ,计算公式如下:$$ \begin{split} &{p_{i,k}}' = \prod\limits_{j = 2}^i {H_j^{(j,k)}{p_{i,k}}} \\& {\rm s.t.}\;i = 1,2,\cdots,N,\;\;k = 1,2,\cdots,m \\[-3pt] \end{split} $$ (12) 不同于GSP(Global Similarity Prior)优先评估全局相似性[15],文中创新性地提出逐网格优化的方法,通过实验去求取全局最优解,解矩阵的数量级随着图像数量的增多呈现指数增长。而GSP方法处理超过上百张图像时,无法求取解矩阵,不适用于文中的大批量远红外图像的拼接场景。
-
文中引入一个代表重叠区域灰度差异的参数
$D$ ,即当前图像与拼接重叠区的灰度差值。假设${G_i}$ 为单张远红外图像${I_i}(i = 1,2,\cdots,n)$ 的灰度均值,则灰度模板(全部图像的灰度均值)计算公式如下:$$ {G_m} = \frac{1}{n}\sum\limits_{i = 1}^n {{G_i}} $$ (13) 式中:
$n$ 为图像数量。将每张图像的灰度值对比模板图像,并令其灰度分布趋近于模板图像,并同时计算当前图像与其相邻图像重叠区域的灰度均值,假设与当前图像的灰度均值${G_i}$ 的差值为${D_i}$ ,则调节图像灰度分布的公式如下:$$ h(i,j) = \alpha (g(i,j) + {G_m} - {G_i} + {D_i}) $$ (14) 式中:
$g(i,j) $ 和$h(i,j) $ 分别表示调整前后每个图像的单个像素的灰度值;${D_i} $ 为当前图像灰度均值与其相邻图像重叠区域灰度均值的差值。在进行灰度校正后,可以令所有图像的灰度值范围趋近于一致。 -
图像拼接流程如图7所示,具体步骤如下:
(1)输入图像,将图像划分为顺序图像序列和列间图像序列。
(2)顺序图像序列拼接阶段,基于非极大值抑制原理求取单应性矩阵,并推导传递关系。
(3)列间图像序列拼接阶段,使用RANSAC方法对特征点分组计算区域相似矩阵、使用柯西分布计算特征点贡献权重计算局部单应矩阵,逐网格优化变换矩阵的权重。
(4)通过网格变换实现变换矩阵的递推。
(5)使用改进的模板灰度校正方法对图像灰度进行校正得到最终的拼接图像。
-
文中实验的硬件设备为台式计算机,3.4 GHz主频的处理器,8 GB内存。评估实验采用的远红外图像数据集中单张图像分辨率为640×480。共计两组图像数据集,第一组共计41列,每列30张;第二组共计34列,每列33张。整体拼接效果的评估难以量化,文中使用RMSE值评判列与列之间的配准精度,分析了文中使用的灰度校正的方法对拼接效果的影响,各拼接方法在拼接时间上的对比,证明了文中提出的方法在两组图像数据集上的适用性。
-
选取第一组图像的第一列,对顺序图像序列的拼接作对比实验。首先依照可见光图像的拼接方法,逐张循环拼接,随着拼接的图像越来越多,单列图像底部出现畸变,在拼接第12张图像时,畸变严重,与已完成拼接的顺序图像无法匹配到特征点,拼接失败。而文中基于非极大值抑制来求取单应性矩阵,结合单应变换的递推进行多图拼接,能够完成该列顺序图像序列的拼接,其结果如图8所示。
-
利用拼接完成的前7列,文中进行列间拼接的对比实验。图9中分别是APAP、AANAP和文中使用方法的结果。APAP方法未完成7列图像的拼接,其前两列完美对齐了图像的重叠区域,但由于约束不够,其非重叠区域发生畸变,导致后续拼接难以对齐重叠区域,且畸变更加严重,最终拼接失败。AANAP方法结合局部单应性与全局相似变换,能够完成拼接,但由于图像过长,各区域相似性并不相同,仅使用全局相似性来约束图像,部分网格使用的相似矩阵会存在偏差,导致对齐错误。文中使用的方法能够完成7列图像的拼接,且未发生畸变,拼接效果较为理想。

图 9 单列图像、列间图像拼接结果对比
Figure 9. Comparison of stitching results of single column image stitching and inter column image
均方根误差(RMSE)能够反映特征点在经过透视变换前后的误差大小,其值越小意味着变换后的图像与参考图像的差异越小,更利于后续图像拼接。RMSE定义如下:
$$ \begin{split} \\ {\rm RMSE} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{({P_i}' - {P_i})}^2}} } \end{split} $$ (15) 为验证所用拼接方法的准确性,文中给出图10所示的两组远红外图像对,包括:单张红外图像对(图(a))、列红外图像对(图(b)),单张图像的分辨率均为640×480,其用于测试顺序图像序列连续拼接的性能;列图像的分辨率均为800×10000,其用于测试多列图像之间的拼接性能。
公式(15)中,
${P_i}$ 和${P_i}'$ 分别表示参考图像和经过单应性变换的图像之间的匹配点,$n$ 表示匹配点数量。如果配准很准确,那么每一对匹配点都重合,RMSE的值越小,配准效果越好。所提算法与APAP、AANAP和GSP就两组远红外图像对进行对比实验,实验结果如图11所示,文中使用的方法能够得到更准确的对齐结果。图像拼接边缘的畸变对图像拼接质量影响显著。文中通过使用公式(9)计算特征点贡献权重,其图像拼接边缘如图12(b)所示,拼接边缘未出现形变。而使用高斯分布函数计算特征点的贡献权重,图像拼接边缘出现了波浪形畸变,如图12(a)所示。
文中提出使用的柯西分布函数,其与高斯分布函数相比形态更加稳健,波峰更低,尾部衰减更加缓慢,边缘即便远离所有特征点,也会获得相似的加权,导致图像边缘畸变较小。
灰度校正方法是影响红外图像拼接质量的重要因素。校正前的拼接结果如图13(a)所示,拼接大图中存在很多亮度不均匀的区域,且过渡线较明显,灰度均匀性较差。文中使用公式(14)校正改进的模板灰度,得到的灰度校正结果如图13(b)所示,整体灰度均匀性极佳,具有自然的观感。
-
在第一组图像数据集上,文中算法与APAP、AANAP、GSP三种方法进行对比实验。图像数据集共计41列,各方法针对多列图像拼接的数量对比如表2所示。其中APAP和AANAP都由于畸变的累积,分别在完成第4、19列图像的拼接后无法继续拼接,而文中的方法可以完成全部41列的拼接。
表 2 各方法对多列图像拼接数量对比
Table 2. Number comparison of multi-column image mosaic with various methods
Stitching method APAP AANAP GSP Ours Stitching rows 4 19 13 41 文中对比了市面上主流软件对于红外图像数据的拼接效果。使用主流软件AutoStitch、PTGui、ICE(Microsoft Image Composite Editor)和文中方法针对第一组远红外图像数据集进行拼接,其中AutoStitch拼接失败,未生成结果图。拼接速度和拼接结果分别如表3和图14所示。
表 3 主流软件远红外图像拼接速度表
Table 3. Comparison of far-infrared image stitching speed
Software AutoStitch PTGui ICE Proposed Time Failed About
15 minAbout
130 min7 min and
42 s由图14可知,PTGui没有完美对齐图像,只实现了上半部分的图像对齐,而下半部分存在部分偏差,能明显看到公路和湖泊的断层。PTGui拼接速度较快,约15 min完成拼接。ICE通过逐张对比搜索图像位置,自动程度高,但拼接耗时较长,约130 min。
ICE软件和文中方法的拼接结果类似,都较好地完成拼接,但文中方法所需时间更短。
为证明文中提出方法的通用性,在第二组图像数据集上进行对比实验。第二组共计34列,使用APAP、AANAP和GSP三种方法均未实现完整图像的拼接。上一实验中,与文中方法结果接近的ICE软件,拼接效果如图15(a)所示,图像存在黑洞,大片湖泊的区域出现了无法拼接的问题。文中方法可以完成全部图像的拼接,拼接效果如图15(b)所示。
-
文中提出了一种有效处理非一致重叠率的大批量远红外图像的拼接方法,先将图像数据集划分为顺序图像序列和列间图像序列;在顺序图像拼接阶段,创新性地提出一种基于非极大值抑制原理求取单应性矩阵的方法,并推导传递关系;在列间图像拼接阶段,通过划分区域和网格,使用RANSAC方法对特征点分组计算区域相似矩阵,创新性地使用柯西分布计算特征点贡献权重计算局部单应矩阵,逐网格优化变换矩阵的权重并进行递推;最后使用改进的模板灰度校正方法,令所有图像的灰度值范围趋近于一致。
在完成大批量远红外图像拼接工作的同时,文中所提方法具有配准和对齐精确、拼接畸变小、结构保持能力强以及拼接图观感自然等优势。该方法可以应用于许多特殊的拼接场景,例如城市全景图像、遥感图像和其他宽视野图像的拼接,对于军事以及其他行业都具有一定的理论和实践价值。
Research on the stitching method of massive aerial far-infrared images with an inconsistent overlap rate
-
摘要: 由于远红外图像存在分辨率低、具有大量重复结构和稀疏结构等问题,大批量远红外图像的拼接工作面临很多挑战。文中针对航空场景下的远红外图像拼接,将图像对齐过程分为顺序图像序列对齐和多列图像对齐。单列图像基于非极大值抑制求取单应性矩阵,并推导传递关系进行拼接。列间图像通过划分网格,结合区域相似变换和局部单应变换逐网格优化变换矩阵的权重,并通过网格变换的递推实现拼接。文中所述的拼接方法能够避免连续多张远红外图像拼接时导致的特征消失问题,同时适应多列图像拼接时上下重叠率不一致的问题,最终实现了大批量远红外图像的拼接。Abstract: Far-infrared images have problems such as low resolution, large numbers of repetitive structures and sparse structures. The stitching of this type of far-infrared image faces many challenges. Aiming at the far-infrared image stitching in aerial scenes, this paper divides the image alignment process into sequential image sequence alignment and multicolumn image alignment. Single-column images are based on nonmaximum suppression to obtain the homography matrix, and the transfer relationship is derived for splicing. The image stitching between columns is divided into grids, combined with regional similarity transformation and local homography transformation to optimize the weight of the transformation matrix grid by grid and through the recursion of grid transformation to achieve precise stitching. The methods used can avoid the problem of disappearance of splicing features of multiple consecutive far-infrared images and adapt to the problem of inconsistent overlap rate when in multicolumn image stitching, realizing the stitching of massive far-infrared images.
-
Key words:
- image stitching /
- far-infrared images /
- mesh optimization /
- homography matrix
-
表 1 单应性矩阵的权重分布表
Table 1. Weight distribution of homography matrix
Position of
grid kProportion of local
homography matrixProportion of linearizated local
homography matrixProportion of regional similarity
homography matrix${x_{\min }} < {x^{(k)}} < {x_{lc}}$ 0% 0% 100% ${x_{lc}} < {x^{(k)}} < {x_l}$ 0% -100% 0% - 100% 0% -100% ${x_l} < {x^{(k)}} < {x_r}$ 0% 100% 0% ${x_r} < {x^{(k)}} < {x_{rc}}$ 0% - 100% 0% - 100% 0% - 100% ${x_{rc}} < {x^{(k)}} < {x_{\max }}$ 0% 0% 100% 表 2 各方法对多列图像拼接数量对比
Table 2. Number comparison of multi-column image mosaic with various methods
Stitching method APAP AANAP GSP Ours Stitching rows 4 19 13 41 表 3 主流软件远红外图像拼接速度表
Table 3. Comparison of far-infrared image stitching speed
Software AutoStitch PTGui ICE Proposed Time Failed About
15 minAbout
130 min7 min and
42 s -
[1] Lowe D G. Distinctive image features from scale-invariant keypoints [J]. International Journal of Computer Vision, 2004, 60(2): 91-110. doi: 10.1023/B:VISI.0000029664.99615.94 [2] Bay H, Ess A, Tuytelaars T, et al. Speeded-up robust features (SURF) [J]. Computer Vision and Image Understanding, 2008, 110(3): 346-359. doi: 10.1016/j.cviu.2007.09.014 [3] Bian J W, Lin W Y, Matsushita Y, et al. GMS: Grid-based motion statistics for fast, ultra-robust feature correspon-dence[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017: 4181-4190. [4] Fan P Q, Wu C, Yang R Y, et al. An improved SURF infrared image stitching method based on BRISK [J]. Infrared Technology, 2018, 32(1): 27-33. (in Chinese) doi: 1001-8891(2018)01-0027-07 [5] Alam M S, Bognar J G, Hardie R C, et al. Infrared image registration and high-resolution reconstruction using multiple translationally shifted aliased video frames [J]. IEEE Transactions on Instrumentation and Measurement, 2000, 49(5): 915-923. doi: 10.1109/19.872908 [6] Wang Y H, Feng Y, Cao Y, et al. Application of grayscale nonuniformity correction in infrared image sequence mosaic [J]. Infrared, 2011, 32(9): 19-28. (in Chinese) doi: 10.3969/j.issn.1672-8785.2011.09.005 [7] Zaragoza J, Chin T J, Tran Q H, et al. As-projective-as-possible image stitching with moving DLT [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(7): 1285-1298. doi: 10.1109/TPAMI.2013.247 [8] Chang C H, Sato Y, Chuang Y Y. Shape-preserving half-projective warps for image stitching[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2014: 3254-3261. [9] Lin C C, Pankanti S U, Natesan R K, et al. Adaptive as-natural-as-possible image stitching[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2015: 1155-1163. [10] Tang J, Liang Y H, Guo F, et al. Sequential far infrared image mosaic using coarse-to-fine scheme [J]. IEEE Access, 2019, 7: 70185-70199. doi: 10.1109/ACCESS.2019.2918805 [11] Peng C, Li G Z, Zhang X Y, et al. Research on infrared remote sensing image Mosaic based on improved ORB algorithm [J]. Control Engineering, 2020(8): 32-1336. (in Chinese) [12] Webster E A G, Rhodes H E, Massetti D. Visible and infrared image sensor, US: US Patent 9, 806, 122[P]. 2017-10-31. [13] Pei X. Research on infrared image registration and mosaic algorithm in vehicle moving platform[D]. Xi'an: Xidian University, 2020. (in Chinese) [14] Che C, Lan W B. Infrared panoramic image stitching based on Canny algorithm and median filter method [J]. Laser Magazine, 2020, 41(5): 109-113. (in Chinese) [15] Chen Y S, Chuang Y Y. Natural image stitching with the global similarity prior[C]//European Conference on Computer Vision. Cham: Springer, 2016: 186-201. -






 下载:
下载: