-
渐进多焦点眼用镜片具有光焦度从镜片上部到下部连续变化的特点，能够避免传统老花镜不能同时满足老花眼患者看远和看近的缺点，实现了人们只要佩戴一副眼镜就能同时看清远距离、中距离和近距离的物体，极大地方便了生活[1]。因此，渐进多焦点眼用镜片的应用前景非常广阔。
渐进多焦点眼用镜片的面形是影响眼用镜片质量的重要因素之一，其中眼用镜片的子午线是面形设计的首要环节。常用的子午线设计以及优化方法有：选择一条高阶多项式描述镜片子午线，根据不同的需求，设定相应的边界条件，得到视远区或视近区光焦度分布情况不同的子午线，设计视近或视远用途为主的镜片[2]，但该方法不能控制渐进通道附近的光焦度分布情况，得到的镜片渐进通道较窄，无法设计中距离用途为主的镜片；利用遗传算法不依赖具体优化目标以及稳定性强的特点，用二进制字符串（染色体）表示描述渐进多焦点眼用镜片子午线的多项式系数，采用罚函数法以及线性加权法将渐进多焦点眼用镜片的光焦度和散光这两个目标规划成单目标函数。目标函数进行选择、交叉和变异，产生新一代染色体种群，循环搜索子午线最优系数，使镜片的光焦度和像散分布都得到了改善[3]，但遗传算法的编程较为复杂，对于交叉率、变异率等参数的选择也较为困难，使用该算法优化子午线时会导致计算时间增加，优化效率低以及影响解的品质，难以普及应用；确定镜片视远区和视近区光焦度，引入平移和缩放因子构造一个双曲正切函数描述子午线光焦度变化，通过平移和缩放因子自由地控制视远区、视近区位置以及渐进通道长度[4]，该方法得到的镜片渐进通道仍然较窄，无法通过该方法设计中距离用途为主的镜片；也有根据佩戴者的生理数据（如身高、瞳距、近眼距等）和视觉习惯（平时工作和阅读的距离、选用镜框等）设计子午线加光曲线，实现个性化设计[5-6], 但设计过程效率不高。文中提出了一种利用两条高阶多项式拟合子午线光焦度变化曲线的方法，与上述子午线设计以及优化方法相比，该方法拥有更多控制子午线光焦度增加速率的变量，可以更加灵活、自由地调整镜片视远区和视近区光焦度和像散，增大渐进通道的宽度，提高老花眼患者的佩戴体验。
-
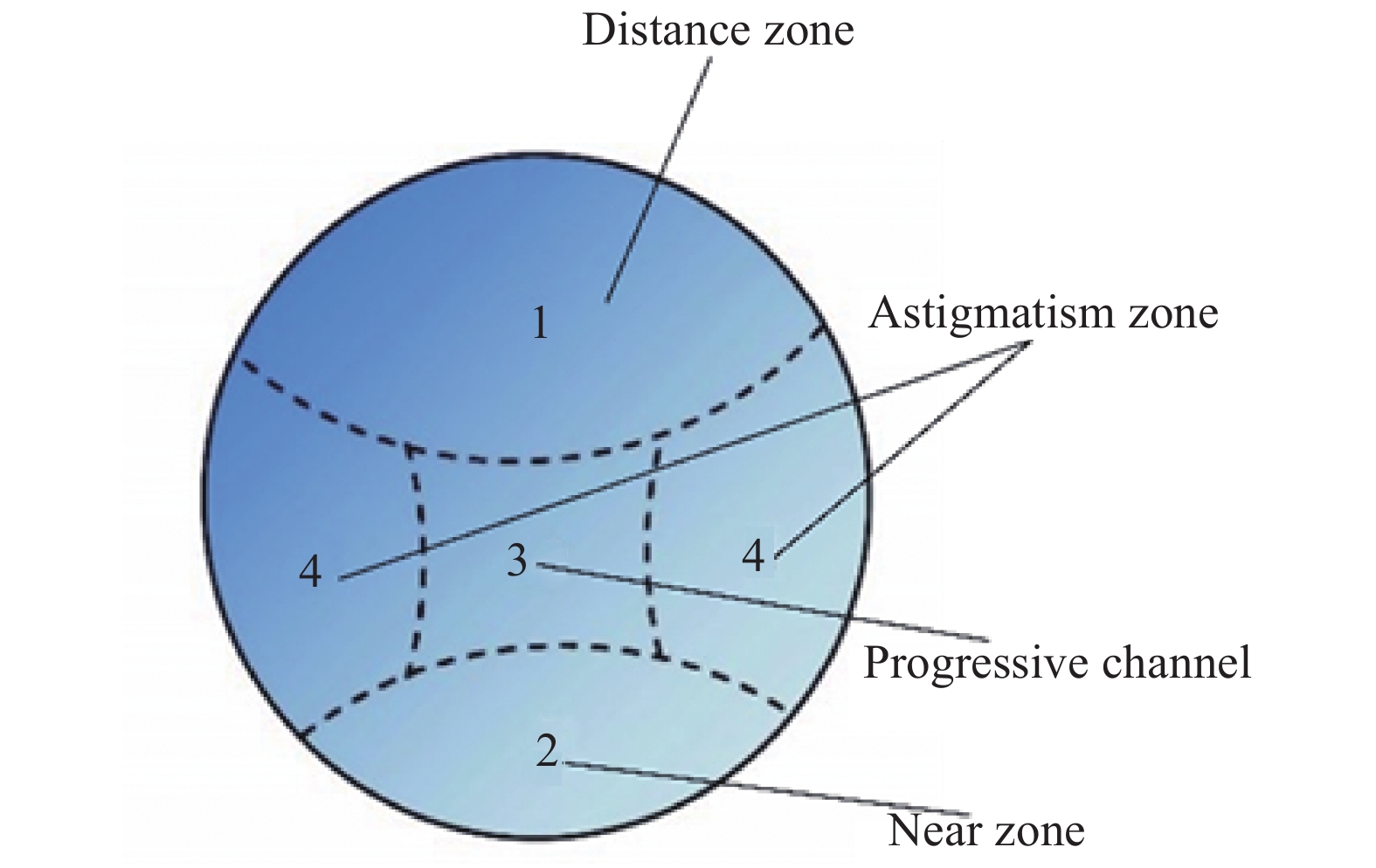
渐进多焦点眼用镜片的表面是一种非旋转对称的非球面，图1所示为渐进多焦点眼用镜片渐变面分区示意图。渐变面主要分为四个区域：1区为视远区，2区为视近区，3区为渐进通道，用于连接视远区和视近区，4区为像散区。
图 1 渐进多焦点眼用镜片分区示意图
Figure 1. Schematic diagram of areas of progressive addition lenses (PALs)
渐变面的光焦度从视远区到视近区平滑连续地增加，增加的光焦度称为加光量(ADD)。当人眼看远处的物体时，使用镜片的视远区1区，视远区具有较小的光焦度，能够将远处的物体清晰成像在视网膜上。镜片的视近区（2区）具有较大的光焦度，能够将近处的物体清晰成像在视网膜上。连接视远区和视近区的渐进通道具有连续变化的光焦度，介于远近之间的物体在该区域中总能找到与之对应的光焦度，使得该距离的物体能够清晰地成像在视网膜上。渐进通道区域两侧的像散区（4区）对视觉成像产生不利的影响。视远区、视近区以及渐进通道区并称为有效视觉区。性能较好的渐进多焦点眼用镜片应该具有较大的有效视觉区，渐进通道宽，周边像散区像散小且分布均匀[7]。
-
渐进多焦点眼用镜片渐变面（xy平面）如图2所示，子午线MM′ 平分整个镜面，点A和点B分别为视远区参考点和视近区参考点。
图 2 渐进多焦点眼用镜片xy平面示意图
Figure 2. View in vertical elevation (xy) of PALs
-
如图2所示，设视远区参考点A到镜片中心点O的距离为l，则点A在x=−l处，视远区参考点和视近区参考点间的距离为h，则视近点B在x=−l+h处，视远点处的光焦度为DA，加光量为ADD，则视近点处的光焦度为DA+ADD，镜片的折射率为n，子午线MM′上视远点和视近点之间任意一点的光焦度为D(u, 0)，则双向拟合子午线光焦度变化曲线方程为：
$$ D\left( {u,0} \right) = \left\{ \begin{gathered} \sum\limits_{j = 0}^i {{a_j}{u^j}} {\text{ }} - l \leqslant u \leqslant {u_0} \hfill \\ \sum\limits_{j = 0}^i {{b_j}{u^j}} {\text{ }}{u_0} \leqslant u \leqslant - l + h \hfill \\ \end{gathered} \right. $$ (1) 式中：u为子午线上点A和点B之间x坐标值；aj和bj分别为第一段曲线和第二段曲线多项式的系数；u0为这两段曲线连接点的x坐标值；i为两个多项式的最高次幂。
由子午线光焦度变化曲线（图3）可见，子午线由两条高阶多项式曲线拟合而成，这里称拟合点为子午线形状控制点P，为了保证两条曲线平滑连接，子午线形状控制点处应具有相同的一阶导数，设其值为k0，通过选择不同的k0值控制子午线渐进通道处光焦度增加速率，从而灵活地调整通道宽度。
图 3 子午线光焦度变化曲线
Figure 3. Focal power curves of the meridian line
已知视远点的位置x=l和光焦度DA，视近点的位置x=−l+h和光焦度DA+ADD，所以有如下等式：
$$ \left\{ \begin{gathered} D\left( {u,0} \right)\left| {_{u = - l}} \right. = {D_A} \hfill \\ D\left( {u,0} \right)\left| {_{u = - l + h}} \right. = {D_A} + ADD \hfill \\ \end{gathered} \right. $$ (2) 由于子午线形状控制点P的位置为（u0，D0），一阶导数为k0，所以有如下等式：
$$ \left\{ \begin{gathered} D(u,0)\left| {_{u = {u_0}}} \right. = {D_0} \hfill \\ \frac{{\rm{d}}}{{{\rm{d}}u}}\left( {D\left( {u,0} \right)} \right)\left| {_{u = {u_0}}} \right. = {k_0} \hfill \\ \end{gathered} \right. $$ (3) 为了使视远点和视近点处的光焦度增加缓慢，从而使该处的像散较小，所以曲线在视远参考点以及视近参考点处的高阶微分导数应满足方程（4）：
$$ \left\{ \begin{gathered} \frac{{{{\rm{d}}^m}}}{{{\rm{d}}{u^m}}}\left( {D\left( {u,0} \right)} \right)\left| {_{u = - l}} \right. = 0 \hfill \\ \frac{{{{\rm{d}}^m}}}{{{\rm{d}}{u^m}}}\left( {D\left( {u,0} \right)} \right)\left| {_{u = - l + h}} \right. = 0 \hfill \\ \end{gathered} \right. $$ (4) 式中：m为视远参考点以及视近参考点出现为零的高阶微分导数的阶数，m=i−2。
根据公式（2）~（4）可以得到增广矩阵（5），由增广矩阵（5）可以解得第一条曲线的系数a0，a1，a2，…，ai。同理，由公式（2）~（4）也可以得到增广矩阵（6），解得第二条曲线的系数b0，b1，b2，…，bi。再由公式（1）获得子午线光焦度变化曲线图。子午线形状控制点P在子午线上的位置u0、光焦度D0以及一阶导数k0取值决定了光焦度增加速率，即子午线的形状。
$$ \left[ {\begin{array}{*{20}{c}} {{{\left( { - l} \right)}^0}}&{ - l}&{{{\left( { - l} \right)}^2}}& \cdots &{{{\left( { - l} \right)}^{i - 1}}}&{{{\left( { - l} \right)}^i}}&{{D_A}} \\ {{{\left( {{u_0}} \right)}^0}}&{{u_0}}&{{{\left( {{u_0}} \right)}^2}}& \cdots &{{{\left( {{u_0}} \right)}^{i - 1}}}&{{{\left( {{u_0}} \right)}^i}}&{{D_0}} \\ 0&{{{\left( {{u_0}} \right)}^0}}&{{u_0}}& \cdots &{\left( {i - 1} \right){{\left( {{u_0}} \right)}^{i - 2}}}&{i{{\left( {{u_0}} \right)}^{i - 1}}}&{{k_0}} \\ 0&0&{{{\left( {{u_0}} \right)}^0}}& \cdots &{\left( {i - 1} \right)\left( {i - 2} \right){{\left( { - l} \right)}^{i - 3}}}&{i\left( {i - 1} \right){{\left( { - l} \right)}^{i - 2}}}&0 \\ \vdots & \vdots & \vdots & \cdots & \vdots & \vdots & \vdots \\ 0&0&0& \cdots &{\left( {i - 1} \right) \cdots \left( {i - m + 2} \right){{\left( { - l} \right)}^{i - m + 1}}}&{\left( i \right) \cdots \left( {i - m + 1} \right){{\left( { - l} \right)}^{i - m}}}&0 \end{array}} \right] $$ (5) $$ \left[ {\begin{array}{*{20}{c}} {{{\left( { - l + h} \right)}^0}}&{ - l + h}&{{{\left( { - l + h} \right)}^2}}& \cdots &{{{\left( { - l + h} \right)}^{i - 1}}}&{{{\left( { - l + h} \right)}^i}}&{{D_A} + ADD} \\ {{{\left( {{u_0}} \right)}^0}}&{{u_0}}&{{{\left( {{u_0}} \right)}^2}}& \cdots &{{{\left( {{u_0}} \right)}^{i - 1}}}&{{{\left( {{u_0}} \right)}^i}}&{{D_0}} \\ 0&{{{\left( {{u_0}} \right)}^0}}&{{u_0}}& \cdots &{\left( {i - 1} \right){{\left( {{u_0}} \right)}^{i - 2}}}&{i{{\left( {{u_0}} \right)}^{i - 1}}}&{{k_0}} \\ 0&0&{{{\left( { - l + h} \right)}^0}}& \cdots &{\left( {i - 1} \right)\left( {i - 2} \right){{\left( { - l + h} \right)}^{i - 3}}}&{i\left( {i - 1} \right){{\left( { - l + h} \right)}^{i - 2}}}&0 \\ \vdots & \vdots & \vdots & \cdots & \vdots & \vdots & \vdots \\ 0&0&0& \cdots &{\left( {i - 1} \right) \cdots \left( {i - m + 2} \right){{\left( { - l + h} \right)}^{i - m + 1}}}&{\left( i \right) \cdots \left( {i - m + 1} \right){{\left( { - l + h} \right)}^{i - m}}}&0 \end{array}} \right] $$ (6) -
轮廓线为与子午线正交的曲线簇，每一条轮廓线与子午线相交，轮廓线上的光焦度等于交点处的光焦度，这样就可以得到整个表面的光焦度。采用公式（7）作为轮廓线函数[8-9]：
$$ \left\{ \begin{array}{l} {{u}} = u(x,y) = x, = h/2 - l\\ {{u}} = u(x,y) = h/2 - l + g - {({g^2} - {h^2}/4)^{1/2}},x\ge h/2 - l\\ {{u}} = u(x,y) = h/2 - l + g - {({g^2} - {h^2}/4)^{1/2}},x\le h/2 - l \end{array} \right. $$ (7) 其中，
$ g = \left[ {d + ({y^2} + {h^2}/4)/d} \right]/2;d = x - 2/2 + l $ 。 -
由镜片整个表面的屈光度分布可以计算得到镜片表面各屈光度对应的曲率半径分布[10]：
$$ r(u) = \frac{{n - 1}}{{D(u)}} $$ (8) 式中：n为镜片折射率。
以曲率半径和对应的曲率中心构建一系列的圆，这些圆的包络面即为镜片的表面[11-12]，镜片表面矢高的计算公式为：
$$ z(x, y)=\zeta(u)-\sqrt{r(u)^{2}-[x-\zeta(u)]^{2}-[y-\eta(u)]^{2}} $$ (9) 式中：(ξ, η, ς)为每个球面对应的曲率中心坐标。其计算公式如下：
$$ \left\{\begin{array}{l} \xi(u)=u-r(u) \sin \theta \\ \eta(u)=0 \\ \varsigma(u)=r(u) \cos \theta+\displaystyle\int_{0}^{u} \tan \theta {\rm{d}} u \\ \sin \theta=\displaystyle\int_{0}^{u} \dfrac{{\rm{d}} u}{r(u)} \end{array}\right. $$ (10) -
使用渐变表面的平均球面度D和柱面度C来评价渐进多焦点眼用镜片的光学性能[13-14]：
$$ D = \frac{{n - 1}}{2}\left( {\frac{1}{{{r_1}}} + \frac{1}{{{r_2}}}} \right) $$ (11) $$ C = (n - 1)\left( {\frac{1}{{{r_1}}} - \frac{1}{{{r_2}}}} \right) $$ (12) 式中：r1和r2分别表示渐进表面上某一点处的最小和最大曲率半径；n为镜片的折射率。
根据明克维茨（Minkwitz）定理：子午线上光焦度的增加速率∂D/∂x和垂直子午线方向上像散的增加速率∂C/∂y之间存在如下关系[15-16]：
$$ \lim _{y \rightarrow 0} \frac{\partial C}{\partial y}=2 \frac{\partial D}{\partial x}=2 \frac{\partial D}{\partial u} $$ (13) 式中：u为子午线的坐标；y为垂直于子午线的距离。
由公式(3)和(13)可得：
$$ \mathop {\lim }\limits_{y \to 0} \frac{{\partial C}}{{\partial y}} = 2\frac{{\partial D}}{{\partial u}}\left| {_{u = {u_0}}} \right. = 2\frac{{{\rm{d}}D}}{{{\rm{d}}u}}\left| {_{u = {u_0}}} \right. = 2{k_0} $$ (14) 从公式(14)可以看出，控制点P处的水平方向像散增加速度是子午线光焦度增加速率k0的两倍。要想使渐进通道两侧的像散变小，可以减小渐进通道处光焦度增加速率k0，从而增加渐进通道的宽度，使佩戴渐进多焦点眼用镜片老花眼患者获得较佳的中距离视野，提升佩戴者的适应度和舒适度。
-
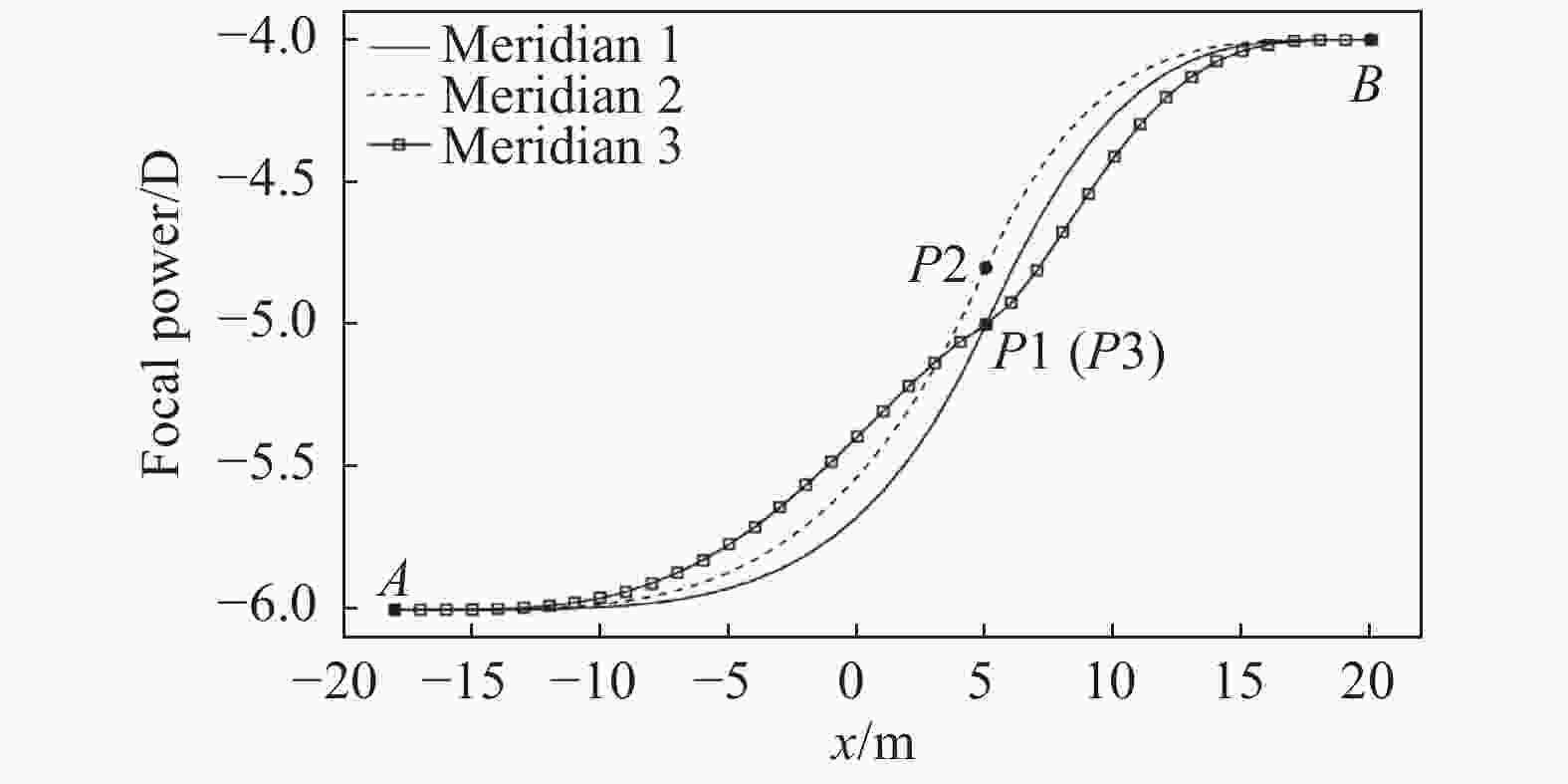
设定镜片参数相同，双向拟合设计子午线P处的参数不同，可以获得适合不同需要的镜片面形。镜片的内表面采用渐进面，镜片视远点A处的光焦度为−6.00 D （屈光度），加光量（ADD）为2.00 D，视近点B处的光焦度为−4.00 D，折射率n为1.56的树脂材料，镜片的半径R取30 mm，选取参考点A和B之间的距离h=32 mm，视远点A与镜片中心之间的距离l=10 mm。分别根据视远为主、视近为主或中间距离为主的使用要求设计子午线，视远为主的镜片在视远区的光焦度变化应最缓慢，形状控制点P处的光焦度参数尽可能小，所以子午线1形状控制点P的参数取值为u0=5.00，D0=5.00，k0=0.20。增大形状控制点P处的光焦度参数可使视近区的光焦度变化缓慢，获得视近为主的镜片，所以子午线2形状控制点P的参数取值为u0=5.00，D0=5.20，k0=0.20。想要获得中间距离为主（宽渐进通道）的镜片，子午线渐进通道附近（形状控制点P附近）的光焦度的变化应该缓慢，形状控制点P处的斜率参数应尽可能小，所以子午线3形状控制点P的参数取值为u0=5.00，D0=5.20，k0=0.02。通过MATLAB软件计算获得对应的渐进多焦点眼用镜片子午线。子午线设计结果如图4所示。
图 4 三种子午线光焦度变化图
Figure 4. Focal power curves for three kinds of the meridian lines
依据渐进多焦点眼用镜片的设计方法得到渐进多焦点眼用镜片的面形，由公式（11）和（12）计算出三种镜片的光焦度和像散分布，如图5和图6所示。
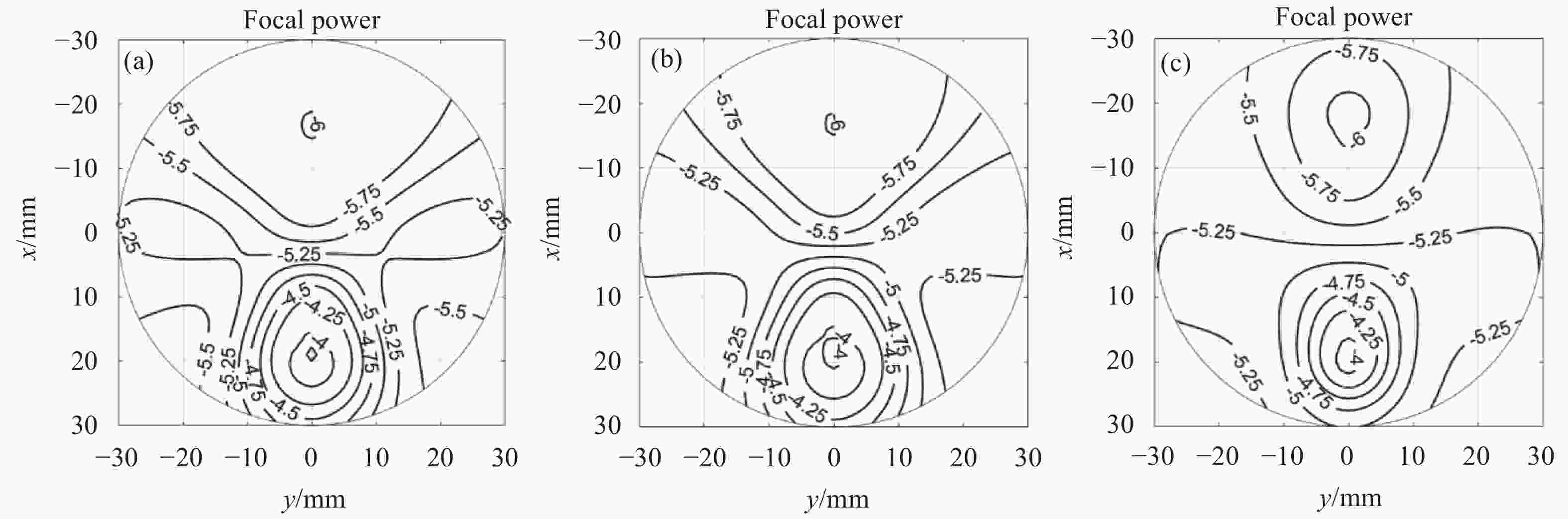
图 5 渐进多焦点眼用镜片光焦度图。 (a)子午线1；(b)子午线2；(c)子午线3
Figure 5. Power of PALs. (a) Meridian 1; (b) Meridian 2; (c) Meridian 3
图 6 渐进多焦点眼用镜片像散图 (a)子午线1；(b)子午线2；(c)子午线3
Figure 6. Astigmatism of PALs. (a) Meridian 1; (b) Meridian 2; (c) Meridian 3
从图4~6可见，尽管镜片的设计参数相同，但拟合的子午线不同，获得的镜片的光焦度和散光分布不同。三条子午线设计的镜片的光焦度在视远区均为−6.00 D，近区均为−4.00 D，加光量都为2.00 D。根据子午线1设计的镜片视远区光焦度误差在0.25 D内的最大宽度最宽（44 mm），视远区光焦度稳定范围最大，视远区像散小于0.50 D的视觉区范围也是最大（48 mm）；根据子午线2设计的镜片视近区光焦度误差在0.25 D范围内的最大宽度最宽（16 mm），视近区光焦度稳定范围三者之中最大，视近区像散小于0.50 D的视觉区范围也是三者之中最大（18 mm）；由子午线3设计的镜片的渐进通道处像散小于0.50 D的最小宽度为6 mm，是由子午线1和子午线2设计的镜片的2倍，且渐进通道两侧的大像散区最大像散也由1.75 D下降到了1.00 D。
-
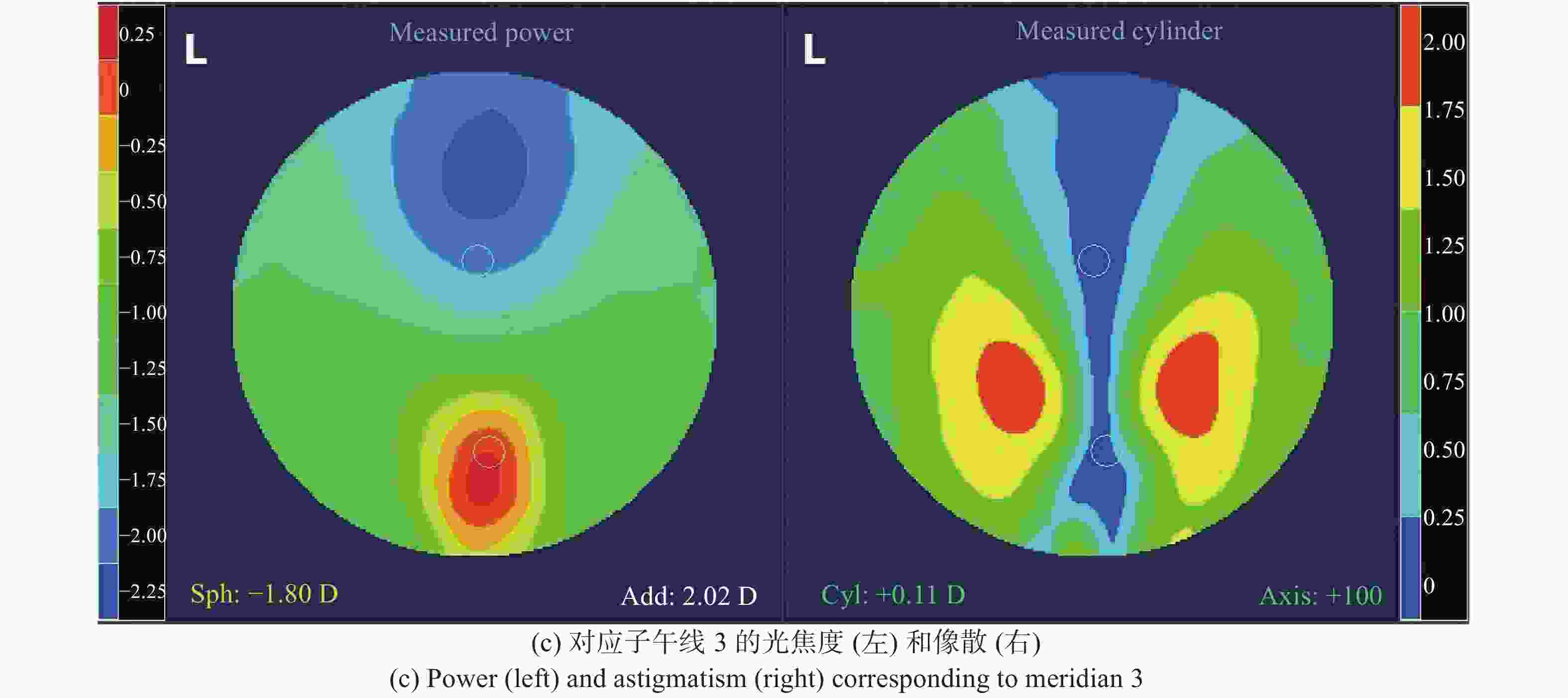
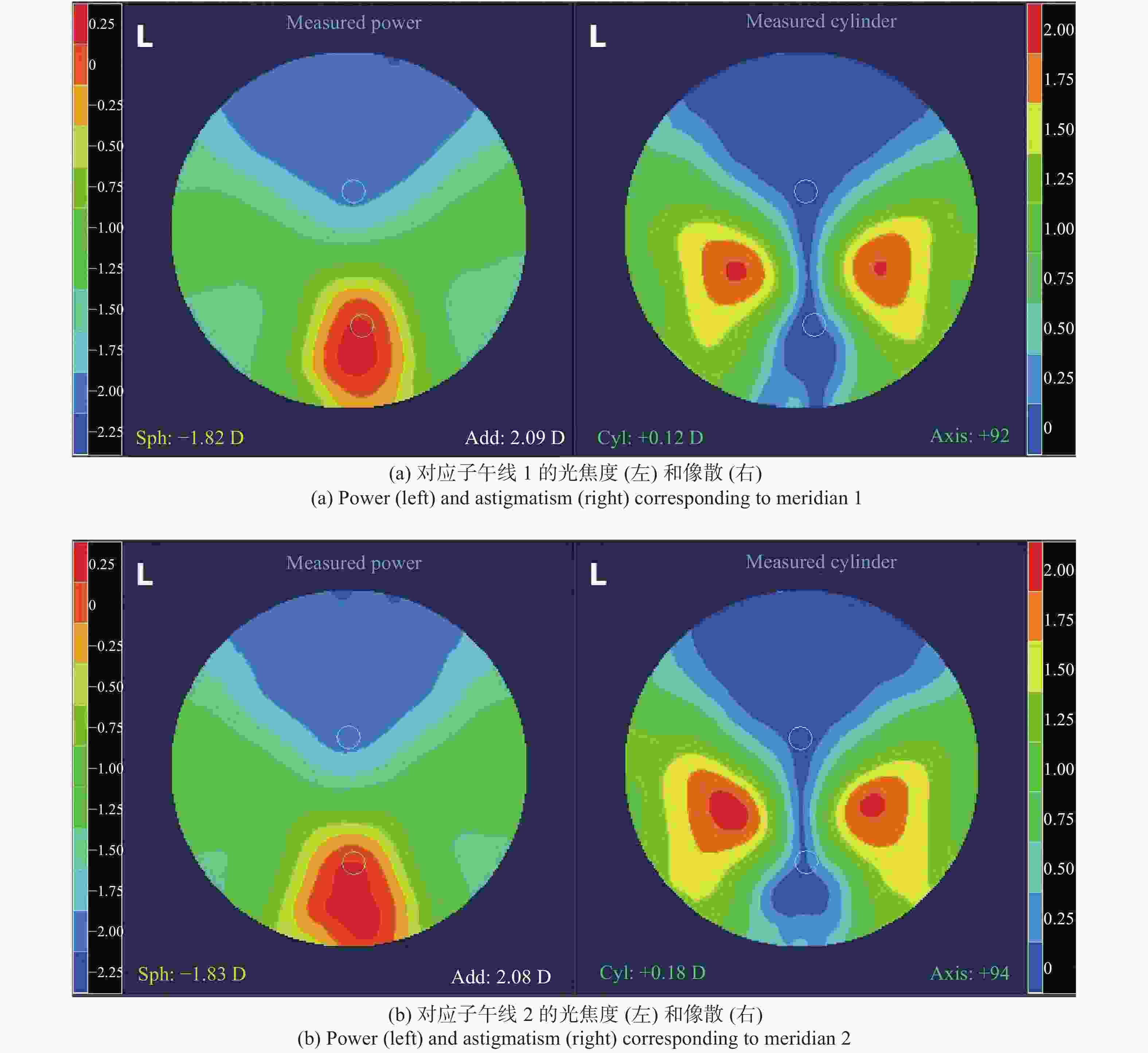
将三个实例的镜片矢高数据z(x, y)输入到数控机床，镜片采用后表面为渐进面，前表面为光焦度为4 D的球面。经过车削、抛光等一系列步骤后完成镜片加工[17]，利用自由曲面检测仪（FFV）测试镜片的光焦度和像散图，如图7所示。
图 7 加工的渐进多焦点眼用镜片光焦度和散光图
Figure 7. Power and astigmatism of manufactured PALs
由图7可以看出，实际镜片的测试结果与镜片模拟结果基本相符。由测试结果（图7）可知，加工的三个镜片的视远区光焦度均为−1.82 D左右，加光度数均约为2.00 D。实际镜片渐进通道的像散值小于0.5 D，图7（a）和图7（b）镜片的最大像散值为2.00 D，图7（a）镜片的大像散区的范围比图7（b）镜片小，图7（c）镜片的最大像散值最小，仅为1.25 D。
镜片的性能参数对比如表1所示。结合图4和图7可知，子午线1光焦度增加速率在视远区附近最为缓慢，根据其设计并加工的镜片拥有最宽阔的视远区范围；子午线2光焦度增加速率在视近区附近最为缓慢，根具其设计并加工的镜片拥有最宽阔的视近区；与子午线1和2相比，子午线3光焦度增加速率在渐进通道处最为缓慢，加工的镜片拥有最宽的渐进通道。
表 1 镜片性能参数对比表
Table 1. Comparison of the lenses performance parameters
Meridian Maximum width of stable power of the distance zone (Error value<0.25 D) Ld/mm Maximum width of the distance zone (Astigmatism<0.5 D) Wd/mm Maximum width of stable power of the near zone (Error value<0.25 D) Ln/mm Maximum width of the near zone (Astigmatism<0.5 D) Wn/mm Minimum width of progressive channel (Astigmatism<0.5 D) d/mm Meridian 1 44 48 12 14 3 Meridian 2 36 44 16 18 3 Meridian 3 22 38 8 10 6 -
子午线的设计是渐进多焦点眼用镜片设计的关键步骤，采用两条高阶多项式拟合获得镜片子午线方程，通过该方程设计渐进多焦点眼用镜片，渐进多焦点眼用镜片的像散大小与子午线上光焦度增加速率存在正相关。不同的子午线分别对应镜片视远区最开阔，适用于视远为主的人群；镜片视近区范围最大，适用于读书、看报、书写等近距离工作为主的人群；镜片渐变通道最宽，具有较宽的中距离视野范围，适用于如使用电脑等中距离用眼为主的人群。通过调整子午线形状控制点的参数（一阶导数、位置、光焦度），可以减小子午线不同位置的光焦度增加速率，增大对应区域的清晰视觉范围，设计满足个性化佩戴需求的渐进多焦点眼用镜片。实际加工镜片表明，镜片加工结果与设计结果相符合。
Bi-directional fitting design of meridian lines for progressive addition lenses
-
摘要: 介绍了渐进多焦点眼用镜片的结构。提出了一种双向拟合设计渐进多焦点眼用镜片子午线的方法，采用两条多项式曲线从镜片视远点和视近点双向拟合，获得满足设计要求的子午线。在此基础上，选择与子午线正交、满足设计要求的曲线簇作为轮廓线，计算镜片上各个点的矢高数据，从而获得整个面形。设计结果表明，与只采用一条高阶多项式曲线描述子午线的方法相比较，双向拟合设计镜片子午线的方法可以灵活地调节子午线上光焦度增加的速率，从而控制镜片视远区、视近区以及渐进通道的光焦度和像散，设计满足眼镜佩戴者个性化需求的渐进多焦点眼用镜片，即当镜片参数相同时，双向拟合子午线不同，可以获得相应视觉需要的渐进多焦点眼用镜片。将设计的镜片进行实际加工，并检测加工结果，结果表明，加工获得的镜片性能与设计结果一致。Abstract: The structure of progressive addition lenses (PALs) was introduced. A method of bi-directional fitting meridians of PALs was proposed. Two polynomial curves were fitted bi-directionally from the far and near points of the PALs to obtain meridians that meet the design requirements. Based on this, the curve cluster which was orthogonal to the meridian and meeting the design requirements was selected as the contour line. The vector height data of each point on the PALs was calculated to obtain the entire surface shape. The design results show that the bi-directional fitting method of designing the PALs′ meridians provides the flexibility to adjust the rate of increase of the focal power on the meridians compared to the single higher-order polynomial curve describing the meridians. The individual needs of the wearers can be met to control the focal power and astigmatism of the PALs in the far and near vision zones as well as in the gradient channel. When the same lenses parameters and different bi-directional fitting meridians are chosen, corresponding demanded visual area can be obtained for PALs. The designed PALs were processed, and the finished PALs were measured. It is shown that the performances of the PALs obtained by processing are consistent with the performances of the designed PALs.
-
Key words:
- optical design /
- progressive addition lenses /
- meridian /
- power /
- astigmatism
-
图 1 渐进多焦点眼用镜片分区示意图
Figure 1. Schematic diagram of areas of progressive addition lenses (PALs)
图 5 渐进多焦点眼用镜片光焦度图。 (a)子午线1；(b)子午线2；(c)子午线3
Figure 5. Power of PALs. (a) Meridian 1; (b) Meridian 2; (c) Meridian 3
图 6 渐进多焦点眼用镜片像散图 (a)子午线1；(b)子午线2；(c)子午线3
Figure 6. Astigmatism of PALs. (a) Meridian 1; (b) Meridian 2; (c) Meridian 3
表 1 镜片性能参数对比表
Table 1. Comparison of the lenses performance parameters
Meridian Maximum width of stable power of the distance zone (Error value<0.25 D) Ld/mm Maximum width of the distance zone (Astigmatism<0.5 D) Wd/mm Maximum width of stable power of the near zone (Error value<0.25 D) Ln/mm Maximum width of the near zone (Astigmatism<0.5 D) Wn/mm Minimum width of progressive channel (Astigmatism<0.5 D) d/mm Meridian 1 44 48 12 14 3 Meridian 2 36 44 16 18 3 Meridian 3 22 38 8 10 6 
下载: 导出CSV
-
[1] Pope D R. Progressive addition lenses: history, design, wearer satisfaction and trends [C]//Vision Science and its Applications, Optical Society of America, 2000: paperNW9. [2] 吴泉英, 钱霖, 陈浩, 等. 渐进多焦点眼用镜片的子午线设计研究[J]. 光学学报, 2009, 29(11): 3186-3191. doi: 10.3788/AOS20092911.3186 Wu Quanying, Qian Lin, Chen Hao, et al. Research on meridian lines design for progressive addition lenses [J]. Acta Optica Sinica, 2009, 29(11): 3186-3191. (in Chinese) doi: 10.3788/AOS20092911.3186 [3] 唐运海, 吴泉英, 陈晓翌, 等. 基于遗传算法的渐进多焦点镜片子午线优化设计[J]. 光学学报, 2014, 34(9): 0922005. doi: 10.3788/AOS201434.0922005 Tang Yunhai, Wu Quanying, Chen Xiaoyi, et al. Optimization design of the meridian line of progressive addition lenses based on genetic algorithm [J]. Acta Optica Sinica, 2014, 34(9): 0922005. (in Chinese) doi: 10.3788/AOS201434.0922005 [4] Qiu Gufeng, Cui Xudong. Hyperbolic tangential function-based progressive addition lens design [J]. Applied Optics, 2015, 54(35): 10404-10408. doi: 10.1364/AO.54.010404 [5] Tang Yunhai, Wu Quanying, Chen Xiaoyi, et al. A personalized design for progressive addition lenses [J]. Optics Express, 2017, 25(23): 28100-28111. doi: 10.1364/OE.25.028100 [6] Wu Quanying, Tang Yunhai, Chen Xiaoyi, et al. Method for evaluating ophthalmic lens based on Eye-Lens-Object optical system [J]. Optics Express, 2019, 27(26): 37274-37285. doi: 10.1364/OE.27.037274 [7] 唐运海. 渐进多焦点眼镜片的优化设计[D]. 苏州: 苏州大学, 2011. Tang Yunhai. Optimizing design of progressive addition lenses[D]. Suzhou: Soochow University, 2011. (in Chinese) [8] 吴泉英, 钱霖, 陈浩, 等. 渐进多焦点镜片的设计方法[J]. 激光杂志, 2009, 30(6): 12-14. doi: 10.3969/j.issn.0253-2743.2009.06.005 Wu Quanying, Qian Lin, Chen Hao, et al. design methods of progressive addition lenses [J]. Laser Journal, 2009, 30(6): 12-14. (in Chinese) doi: 10.3969/j.issn.0253-2743.2009.06.005 [9] 张皓, 唐运海, 吴泉英, 等. 基于拉普拉斯方程的渐进多焦点眼用镜片轮廓线优化设计[J]. 激光与光电子学进展, 2017, 54(11): 112201. Zhang Hao, Tang Yunhai, Wu Quanying, et al. Contour line optimization design of progressive addition lenses based on laplace equation [J]. Laser & Optoelectronics Progress, 2017, 54(11): 112201. (in Chinese) [10] 肖志涛, 娄世良, 耿磊, 等. 便携式免散瞳眼底相机光学系统设计[J]. 红外与激光工程, 2018, 47(8): 818001-0818001(8). doi: 10.3788/IRLA201847.0818001 Xiao Zhitao, Lou Shiliang, Geng Lei, et al. Optical system design of portable non-mydriatic fundus camera [J]. Infrared and Laser Engineering, 2018, 47(8): 0818001. (in Chinese) doi: 10.3788/IRLA201847.0818001 [11] 卢宏炎, 白东峰, 马建文. 渐进多焦点镜片表面初始矢高模型的设计[J]. 激光与光电子学进展, 2017, 54(3): 032201. Lu Hongyan, Bai Dongfeng, Ma Jianwen. Design for initial vector height model of progressive addition lenses surface [J]. Laser & Optoelectronics Progress, 2017, 54(3): 032201. (in Chinese) [12] Casanellas G, Castro J. Using interior point solvers for optimizing progressive lens models with spherical coordinates[J]. Optimization and Engineering, 2020, 21(4): 1389-1421. [13] Xiang Huazhong, Zhang Lu, Gao Jiandong, et al. Weight distributions of spherical and cylindrical power deviations for designing freeform progressive addition lenses [J]. Optics Communications, 2020, 484: 126662. [14] 秦琳玲. 自由曲面镜片的模拟评价方法及优化设计研究[D]. 苏州: 苏州大学, 2014. Qin Linling. Study on simulation method and optimization design of ophthalmic freeform lenses[D]. Suzhou: Soochow University, 2014. (in Chinese) [15] Sheedy J E, Campbell C, King-Smith E, et al. Progressive powered lenses: the Minkwitz theorem. [J]. Optometry and Vision Science, 2005, 82(10): 916-922. doi: 10.1097/01.opx.0000181266.60785.c9 [16] Barbero S, González M D M. Admissible surfaces in progressive addition lenses [J]. Optics Letters, 2020, 45(20): 5656-5659. doi: 10.1364/OL.401927 [17] 李卓霖, 李荣彬. 精密数控抛光碳化硅表面去除特性研究[J]. 红外与激光工程, 2016, 45(2): 220003-0220003(8). doi: 10.3788/irla201645.0220003 Li Zhuolin, Lee W B. Study on removal characteristic of silicon carbide surface in precision mechanical polishing [J]. Infrared and Laser Engineering, 2016, 45(2): 0220003. (in Chinese) doi: 10.3788/irla201645.0220003 -
点击查看大图
图(8) / 表(1)
计量
- 文章访问数: 59
- HTML全文浏览量: 15
- PDF下载量: 32
- 被引次数: 0
