-
激光三维重建技术是一种主动式光学测量技术,对比声呐扫描,激光扫描不易受到海水温度和盐度变化的影响,而且高亮度的激光可以有效地滤出背景光的噪声,得到高于声呐图像像素数百倍的高分辨率的图像[1-4],在水下工程建设、军事需求、科学研究、生物考察、考古学、海底形貌描绘等方面都具有广泛的应用前景[5-8]。水下工程建设方面[9],激光三维重建技术能为水下施工项目提供更精确的可视化三维现场勘测,用于海底仪器结构的检查、水下管道磨损排查;军事应用方面[10],可以利用激光三维重建技术对水下目标进行监视、扫描探测及记录,对水下军事救援工作提供实时数据支持;海洋科研方面[11-12],可利用水下视觉探测技术完成海底资源探查[13]、绘制海底形貌等[14]。
德国Julius-Maximilians-University 大学Michael Bleier等人研制了波长为525 nm的激光扫描系统对水箱内的物体进行静态和动态移动扫描。由得到的点云数据可知,两种状态系统系统的重建误差均小于5 cm[15]。加州大学斯克里普斯海洋学研究所的Jules S. Jaffe 等人发明了应用于水下机器人的线激光扫描成像系统,通过使用大型相机分光、扫描或脉冲系统有效减少后向散射和体积散射。中国海洋大学杨宇等人[16]研究了基于多通道RGB 的激光扫描系统,提出了一种以三基色激光器为主动光源的高分辨率水下真彩色三维重建方法,可以对物体包括人脸,进行毫米量级的扫描和重建的同时还原出目标的真实彩色纹理信息。华北水利水电大学徐望博等人[17]设计并实现了基于多线结构光的水下物体测量系统,在测量距离为2.45 m时,平均误差达到1.6443 mm,具有较高的测量精度。目前许多研究机构针对于图像、点云的处理以及水体散射的校正方面已经做了大量的工作,得到了很好的实验效果。但在水下实验过程中,由于防水装置引起的折射作用对视角误差及成像质量的影响仍需受到更多的关注。
针对于水下目标的高精度三维重建及系统防水装置的折射校正问题,文中设计并研制了基于旋转扫描的水下高精度三维重建系统,提出了防水装置的折射校正算法。并利用已知尺寸的标准球对系统进行误差分析,验证系统的可行性及折射校正算法的有效性。
-
激光三维扫描系统由相机、线激光器、转台和相应的控制装置组成。相机采用华谷动力WP-UT530 M工业相机,分辨率为2592×2048 pixel,光谱范围为380~650 nm;激光器采用波长为520 nm的线形激光器,功率为50 mW;镜头为自主设计的焦距为25 mm,视场角为34°的水下镜头;将相机和激光器分别分装在两个独立的水密装置内,固定在支架上,通过调节导轨上的T型螺母的位置及角度,可以改变激光器和相机的相对角度和位置。由上位机控制转台,使系统可以在50°(垂直)×360°(水平)范围内定点扫描。系统扫描速率为6 (°)/s,最小步距角为0.0625°。系统模型如图1所示。
-
激光条纹体现了被测物体的形状和深度信息,对激光条纹中心线的快速准确提取,是实现激光扫描重建系统高精度高分辨率,提高重建速度的关键图像处理步骤。传统的条纹中心提取算法包括边缘法、阈值法、灰度重心法、模板法、steger算法等。文中使用了将边缘法与高斯拟合算法相结合的方法,在缩短提取时间同时,提高提取精度。提取算法流程图如图2所示。
首先对获得到的图像进行高斯滤波,并计算滤波后的像素点的图像梯幅值,利用Sobel算子得到对应的梯度方向,再通过设定的上下阈值过滤非边缘点。遍历边缘非零像素点后,使用高斯函数进行拟合,将所有边缘像素点的最大值作为条纹中心与拟合的高斯函数进行比较,设定阈值,若位置距离大于阈值,则认为提取的激光条纹中心位置无效。
图3为实验中系统对珊瑚扫描得到的激光条纹图像,处理得到的相应的激光条纹中心提取结果如图4所示,将提取出的激光条纹输出即可得到中心条纹的二维像素坐标。
-
利用条纹中心提取算法得到激光中心条纹的二维像素坐标,通过系统参数标定及坐标系转换公式可将二维图像数据转换成三维点云信息,并根据载体运动方式,实现三维点云数据的拼接。
设激光中心条纹上的任意点在像素坐标系下的位置为
$ \left( {u,v} \right) $ ,在世界坐标系中的位置坐标为$ \left( {{X_W},{Y_W},{Z_W}} \right) $ ,其转换关系为:$$\begin{split} &{Z_c}\left[ {\begin{array}{*{20}{c}} u \\ v \\ 1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\dfrac{1}{{{{{d}}_x}}}}&0&{{u_0}} \\ 0&{\dfrac{1}{{{{{d}}_y}}}}&{{v_0}} \\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} f&0&0&0 \\ 0&f&0&0 \\ 0&0&1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} R&T \\ {\overrightarrow 0 }&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{X_W}} \\ {{Y_W}} \\ {{Z_W}} \\ 1 \end{array}} \right] = \\ & \left[ {\begin{array}{*{20}{c}} {{f_x}}&0&{{u_0}}&0 \\ 0&{f{}_y}&{{v_0}}&0 \\ 0&0&1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} R&T \\ {\overrightarrow 0 }&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{X_W}} \\ {{Y_W}} \\ {{Z_W}} \\ 1 \end{array}} \right]\\[-25pt] \end{split} $$ (1) 式中:
${Z_c}$ 为相机坐标系对应点到相机主点的距离;${{{d}}_x}$ 、${{{d}}_y}$ 分别为单位像素在x轴和y轴方向所对应的物理尺寸;$ {f_x} $ 、$ {f_y} $ 为相机的焦点坐标;R、T分别为相机坐标系相对于世界坐标系的旋转和平移矩阵,可通过在水下,对相机和系统参数的标定获得,避免在光线在通过不同介质时,产生的折射现象对标定结果造成的影响。在水下实验过程中,由于水体对激光的散射作用,图像处理时引入的噪声以及系统标定结果不准确等原因,使得到的三维点云数据不可避免出现一些噪声点,降低系统的重建效率及精度,因此需要对点云数据进行处理。文中采用alpha shapes算法[18]对点云坐标进行特征点提取,实现点云的滤波,随后再利用Delaunay三角剖分算法对滤波后的点云进行曲面重建。
在实验室内对水箱中的目标区域进行扫描重建,实验现场选用水箱尺寸为1.5 m×1.5 m×0.85 m,水体为石老人海水浴场近岸海水。使用功率为50 mW的激光器对水箱内布放的石块、珊瑚、海螺、瓶子等进行旋转扫描,实验现场如图5所示,图6为重建结果。
-
在水下工作中,由于仪器都被要求采用密封的防水装置进行水密处理,使得水下目标和激光扫描系统分隔在不同折射率的介质中,在系统工作时,光线会产生折射现象,折射的影响通常包括两方面,一是密封装置引起密封玻璃处激光平面的偏转,另一个是CCD摄像机物面成像点的位置偏移。针对以上两个问题,文中提出了防水装置折射校正的算法。
如图7所示,空气中的光经过平面A玻璃表面折射可得水下光平面B,
$ {\theta _1} $ 是激光投射角,$ {\theta _2} $ 是光平面A与法线C夹角,$ {\theta _3} $ 是法线A与法线C夹角,$ {\theta _4} $ 是光平面B与法线C夹角,$ {\theta _5} $ 是法线B与法线C夹角。设折射面法向量为(0,0,1),光平面A的法向量为(A,B,C),光平面B法向量为(A’, B’, C’),水与空气的相对折射率为
${n{'}}$ 。由折射定律可得:$$ {n{'}} = \frac{{{n_1}}}{{{n_3}}} = \frac{{\sin {\theta _1}}}{{\sin {\theta _3}}} = \frac{{\cos {\theta _3}}}{{\cos {\theta _5}}} $$ (2) $$ \frac{C}{{\sqrt {{A^2} + {B^2} + {C^2}} }} = {n^{'}}\frac{C}{{\sqrt {{A^{{'}2}} + {B^{{'}2}} + {C^{{'}2}}} }} $$ (3) 因为光平面B法向矢量为:
$$ \sqrt {{A^{'2}} + {B^{'2}} + {C^{'2}}} = 1 $$ (4) 所以有:
$$ {C{'}} = \frac{C}{{{n{'}}\sqrt {{A^2} + {B^2} + {C^2}} }} $$ (5) 由折射定律可知,入射光平面A、折射光平面B、折射界面光平面C三者的法线共面,所以有:
$$ {\left[ {\begin{array}{*{20}{c}} A \\ B \\ C \end{array}} \right]^{\rm T}} = x{\left[ {\begin{array}{*{20}{c}} {{A{'}}} \\ {{B{'}}} \\ {{C{'}}} \end{array}} \right]^{\rm T}} + y{\left[ {\begin{array}{*{20}{c}} 0 \\ 0 \\ 1 \end{array}} \right]^{\rm T}} $$ (6) 联立上述公式可得:
$$ \left\{ {\begin{array}{*{20}{c}} {{A{'}} = \sqrt {\dfrac{{{A^2}{n^{{'}2}}\left( {{A^2} + {B^2} + {C^2}} \right) - {A^2}{C^2}}}{{{n^{{'}2}}({A^2} + {B^2} + {C^2})({A^2} + {B^2})}}} } \\ {{B_1} = \dfrac{{{A_1}B}}{A}} \end{array}} \right. $$ (7) 光平面A和光平面B与玻璃面交点D坐标为
$ \left( {0,H\tan {\theta _1},H} \right) $ ,其中H为摄像机光心到玻璃面的距离,光平面B方程为${A^{'}}x + {B^{'}}y + {C^{'}}\textit{z} + {D^{'}} = 0$ ,将D坐标代入平面光平面方程可得:$$ \left\{ {\begin{array}{*{20}{c}} {{B^{'}}H\tan \theta + {C^{'}}H + {D^{'}} = 0} \\ {BH\tan \theta + CH + D = 0} \end{array}} \right. $$ (8) 综上可得折射后水下的激光平面方程
${A{'}}x + {B{'}}y + {C{'}}\textit{z} + {D{'}} = 0$ 。由图7可知,水中目标
$P{}_W$ 在像平面上的成像点为$ P(u,v) $ ,若在空气中,则直接成像在${P{'}}({u{'}},{v{'}})$ 处,P与P’之间的关系为$\left( {{u{'}},{v{'}}} \right) = \eta \left( {u,v} \right)$ ,则对于每个被测点,只要求得$ \eta $ ,即可实现折射校正。$$ \eta = \frac{{\tan {\theta _7}}}{{\tan {\theta _6}}} = \frac{{\left( {EF\tan {\theta _8} + GF} \right)/{O_c}F}}{{IJ/{O_c}J}} $$ (9) 又因为:
$$ IJ = \sqrt {{u^2} + {v^2}} $$ (10) $$ {O_c}J = f $$ (11) 式中:f为相机焦距。已知
${P{'}}\left( {{x_c},{y_c},{\textit{z}_c}} \right)$ ,在$ {Z_W} \gg H $ 时,可得:$$ \eta = \frac{{\left( {1 - \dfrac{H}{{{z_c}}}} \right)\tan {\theta _8} + \dfrac{H}{{{z_c}}}\tan {\theta _6}}}{{\sqrt {{u^2} + {v^2}} /f}} \approx \frac{{\tan {\theta _8}}}{{\sqrt {{u^2} + {v^2}} /f}} $$ (12) -
采用alpha shapes算法对点云坐标进行特征点提取,实现点云的滤波。alpha shapes算法是由Edelsbrunner H提出的一种简单、有效的快速提取边界点算法,它克服了点云受边界点形状的影响的缺点,能实现快速提取有效的边界点。对点云集中的任一点Q,设滚动圆半径为
$ \alpha $ ,将据离Q$ 2\alpha $ 范围内的所有点记为点集M。具体过程如下:在M内任取一点
$ {Q_1}({x_1},{y_1}) $ ,根据Q和$ {Q_1}({x_1},{y_1}) $ 计算圆心坐标。图8为原理示意图。$ {Q_2} $ 、$ {Q_3} $ 分别为经过$ Q $ 和$ {Q_1} $ 两点,且半径为$ \alpha $ 的两个圆的圆心,坐标计算公式为:$$ {x_2} = x + \frac{1}{2}\left( {{x_1} - x} \right) - \sqrt {\frac{{{\alpha ^2}}}{{\left( {x - {x_1}} \right){}^2 + {{\left( {y - {y_1}} \right)}^2}}} - \frac{1}{4}} \times \left( {{y_1} - y} \right) $$ (13) $$ {y_2} = y + \frac{1}{2}\left( {{y_1} - y} \right) - \sqrt {\frac{{{\alpha ^2}}}{{\left( {x - {x_1}} \right){}^2 + {{\left( {y - {y_1}} \right)}^2}}} - \frac{1}{4}} \times \left( {x - {x_1}} \right) $$ (14) $$ {x_3} = x + \frac{1}{2}\left( {{x_1} - x} \right) + \sqrt {\frac{{{\alpha ^2}}}{{\left( {x - {x_1}} \right){}^2 + {{\left( {y - {y_1}} \right)}^2}}} - \frac{1}{4}} \times \left( {{y_1} - y} \right) $$ (15) $$ \begin{gathered} {y_3} = y + \frac{1}{2}\left( {{y_1} - y} \right) + \sqrt {\frac{{{\alpha ^2}}}{{\left( {x - {x_1}} \right){}^2 + {{\left( {y - {y_1}} \right)}^2}}} - \frac{1}{4}} \times \left( {x - {x_1}} \right) \end{gathered} $$ (16) 计算点集
$ M $ 内除$ {Q_1} $ 外的点分别到$ {Q_2} $ 和$ {Q_3} $ 的距离,若均大于$ \alpha $ ,则$ \alpha $ 为边界点。反之遍历所有点轮换作为$ {Q_1} $ ,直到满足上述条件,该点为边界点。将边界点外的多余点舍去,达到快速滤波效果,提高点云的处理效率。选取适当的半径
$ \alpha $ 值,对点云进行处理,得到滤波后的点云坐标,随后再利用Delaunay三角剖分算法对点云进行曲面重建。Delaunay是实际应用中运用最多的三角剖分。设边$ e $ 是由点集中的点作为端点构成的线段,$ E $ 为$ e $ 集合,点集$ V $ 的三角剖分为$ T = \left( {V,E} \right) $ ,若$ E $ 中的一条边$ e $ (端点为$ a $ ,$ b $ )满足经过$ a $ ,$ b $ 两点的圆内不含$ V $ 内任何其他点,则$ e $ 为Delaunay边。Delaunay三角剖分定义为:若点集$ V $ 的一个三角剖分只包含Delaunay边,那么该三角剖分为Delaunay三角剖分。以海螺为目标物进行水下扫描,基于matlab app designer 编写可视化软件,对海螺进行点云的提取,点云如图9所示。
设置
$ \alpha $ 半径为1,对点云滤波进而曲面重建,重建后的效果图如图10所示。由图10可知系统可以实现对水下目标物体的三维点云坐标提取及曲面重建。
-
为测量系统的精确度,在工作距离500~1200 mm范围内,对半径为20.01 mm的标准球进行扫描重建。在视场内选取12个不同位置,分别计算出不加折射校正算法和加折射校正算法后标准球的测量半径。用R表示未加折射校正算法时水下的测量半径,表示加折射校正后的测量半径。经计算可得标准球半径,条纹提取结果如图11所示。实际测量的标准球半径如表1所示。
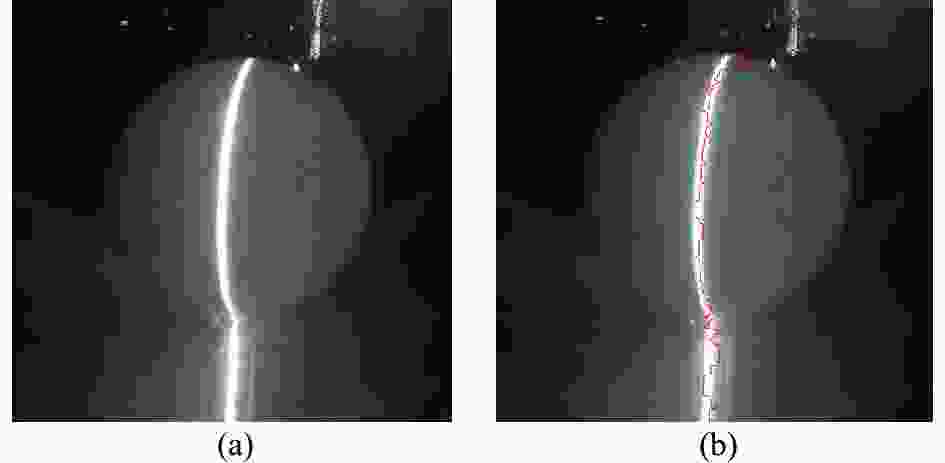
图 11 (a) 水下标准球的误差实验;(b) 水下标准球的条纹中心提取结果
Figure 11. (a) Error experiment of underwater standard ball; (b) Fringe center extraction result of underwater standard
在视场内选取12个不同位置,用半径为20.01 mm的标准球作为被测物体进行测量,完成水下测量实验,通过计算可得标准球的测量半径R,详细测量结果如表1所示。
表 1 标准球的测量结果及误差
Table 1. Measurement result and error of standard ball
Distance/mm R/mm Error/mm ${R_c}$/mm ${\rm Error}{_c}$/mm 500 21.84 1.83 20.12 0.11 550 21.86 1.85 20.09 0.08 600 21.64 1.63 20.20 0.19 650 21.69 1.68 20.23 0.22 700 21.78 1.77 20.30 0.29 750 21.81 1.80 19.74 0.27 800 21.88 1.87 20.35 0.34 850 21.89 1.88 19.65 0.36 900 21.86 1.85 20.47 0.46 950 22.07 2.06 20.50 0.49 1000 21.98 1.97 20.58 0.57 1200 22.12 2.11 19.41 0.6 Average 21.87 1.86 20.14 0.13 Max 22.12 2.11 20.58 0.60 由表1可知,未加折射校正时,标准球的测量误差在2.2 mm范围内,最大测量误差为2.11 mm。加入折射校正后,重建的标准球半径误差范围在0.6 mm内。由此可知:加入了折射校正算法后,系统的重建精度得到了显著提高,证明文中提出的水密装置折射校正算法具有较好的准确性和有效性。
-
文中提出了一种基于旋转扫描的水下线激光三维扫描系统,由线形激光器、水下摄像机机、转台等组成,根据三角测量法,通过对激光中心条纹的形变分析及坐标系转换计算,实现对目标区域三维点云的提取。文中将边缘检测算法与基于极值法的高斯拟合法相结合,同时满足系统对点云重建的速度和精度的要求;利用alpha shapes边界提取算法和Delaunay三角剖分相结合的方法,对点云进行滤波及三维重建,重建效果良好。针对于水下防水装置引起的折射现象对重建精度的影响,文中提出了一种折射校正算法,并用已知尺寸的标准球进行了误差实验。实验结果表明,系统可以实现对水下目标物体及区域的三维形貌还原,重建误差小于0.6 mm,可满足实际需求,具有较好的工程应用前景。
Research on the 3D laser reconstruction method of underwater targets
-
摘要: 文中提出了一种水下线激光的三维重建系统,由相机、绿色线形激光器和转台组成,通过对系统扫描获得的图像进行分析与处理,实现对目标区域的三维重建。采用边缘检测算法与基于极值法的高斯拟合法相结合的条纹中心提取算法,利用坐标转换公式,得到相应的三维点云坐标。点云处理方面,将alpha shapes边界提取算法和Delaunay三角剖分相结合,实现对点云的滤波与重建。针对实验中由于光线在不同介质表面折射造成的视角误差问题,提出了一种折射校正算法,并用已知尺寸的标准球进行了误差实验。结果表明,在500~1200 mm的工作距离内,系统可以实现对水下目标物体及区域的三维形貌还原,重建误差小于0.6 mm,满足设计要求,为水下三维重建技术提供新的参考。
-
关键词:
- 水下三维成像 /
- 线形激光扫描 /
- 条纹中心提取 /
- 三维重建 /
- Delaunay三角剖分
Abstract: A three-dimensional reconstruction system for underwater lasers is proposed, which is composed of a camera, green linear laser and turntable. The three-dimensional reconstruction of the target area is realized by analyzing and processing the image scanned by the system. In the aspect of point cloud processing, this paper combines the alpha shape boundary extraction algorithm and Delaunay triangulation to realize the filtering and reconstruction of point clouds. Aiming at the problem of viewing angle error caused by light refraction on different media surfaces in the experiment, a refraction correction algorithm is proposed, and the error experiment is carried out with a standard ball of known size. The results show that at a working distance of 500-1200 mm, the system can restore the three-dimensional morphology of underwater target objects and regions, and the reconstruction error is less than 0.6 mm, which meets the design requirements and provides a new reference for underwater three-dimensional reconstruction technology. -
表 1 标准球的测量结果及误差
Table 1. Measurement result and error of standard ball
Distance/mm R/mm Error/mm ${R_c}$ /mm${\rm Error}{_c}$ /mm500 21.84 1.83 20.12 0.11 550 21.86 1.85 20.09 0.08 600 21.64 1.63 20.20 0.19 650 21.69 1.68 20.23 0.22 700 21.78 1.77 20.30 0.29 750 21.81 1.80 19.74 0.27 800 21.88 1.87 20.35 0.34 850 21.89 1.88 19.65 0.36 900 21.86 1.85 20.47 0.46 950 22.07 2.06 20.50 0.49 1000 21.98 1.97 20.58 0.57 1200 22.12 2.11 19.41 0.6 Average 21.87 1.86 20.14 0.13 Max 22.12 2.11 20.58 0.60 -
[1] Su Xianyu, Zhang Qican, Chen Wenjing. Structured light 3D imaging technology [J]. Chinese Journal of Lasers, 2014, 41(2): 0209001. (in Chinese) doi: 10.3788/CJL201441.0209001 [2] Xie Zexiao, Li Xuyong, Xin Shaohui, et al. Underwater line structured-light self-scan three-dimension measuring technology [J]. Chinese Journal of Lasers, 2010, 37(8): 2010-2014. (in Chinese) doi: 10.3788/cjl20103708.2010 [3] Xie Liangliang, Tu Dawei, Zhang Xu, et al. Deep sea in situ laser scanning binocular stereo vision imaging system [J]. Journal of Instrumentation, 2020, 41(6): 106-114. [4] Ding Zhongjun, Zhao Ziyi, Zhang Chuntang, et al. 3D reconstruction of deep sea geomorphologic linear structured light based on manned submersible [J]. Infrared and Laser Engineering, 2019, 48(5): 0503001. (in Chinese) doi: 10.3788/IRLA201948.0503001 [5] He X, Tong N, Hu X. High-resolution imaging and 3-D reconstruction of precession targets by exploiting sparse apertures [J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(3): 1212-1220. doi: 10.1109/TAES.2017.2668058 [6] 陈士杰. 海底管道探测与三维可视化技术的研究与实现[D]. 杭州: 浙江大学, 2020. Chen Shijie. Research and implementation of submarine pipeline detection and 3D visualization technology [D]. Hangzhou: Zhejiang University, 2020. (in Chinese) [7] Schjølberg I, Gjersvik T B, Transeth A A, et al. Next generation subsea inspection, maintenance and repair operations [J]. IFAC-Papers OnLine, 2016, 49(23): 434-439. doi: https://doi.org/10.1016/j.ifacol.2016.10.443 [8] Gomes L, Bellon O R P, Silva L. 3D reconstruction methods for digital preservation of cultural heritage: A survey [J]. Pattern Recognition Letters, 2014, 50: 3-14. doi: https://doi.org/10.1016/j.patrec.2014.03.023 [9] Pellen F, Jezequel V, Zion G, et al. Detection of an underwater target through modulated lidar experiments at grazing incidence in a deep wave basin [J]. Appl Opt, 2012, 51: 7690-7700. [10] Meline A, Triboulet J, Jouvencel B. Comparative study of two 3D reconstruction methods for underwater archaeology[C]//Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, 7-12 October 2012, Algarve, Portugal, 2012: 740-745. [11] Eric M, Kovacic R, Berginc G, et al. The impact of the latest 3D technologies on the docu-mentation of underwater heritage sites[C]//Proceedings of the IEEE Digital Heritage International Congress, 28 October-1 November, 2013, Marseille, France, 2013: 281-288. [12] Bruno F, Gallo A, Muzzupappa M, et al. 3D documentation and monitoring of the experi-mental cleaning operations in the underwater archaeological site of Baia (Italy)[C]//Proceedings of the IEEE Digital Heritage International Congress, 28 October-1 November, 2013, Marseille, France, 2013: 105-112. [13] Johnson-Roberson M, Bryson M, Friedman A, et al. High-resolution underwater robotic vision-based mapping and three-dimensional reconstruction for archaeology [J]. J Field Robot, 2017, 34: 625-643. doi: https://doi.org/10.1002/rob.21658 [14] Jørgensen U, Skjetne R. Real-time 3D reconstruction of under-water sea-ice topography by observations from a mobile robot in the arctic [J]. IFAC Proceedings Volumes, 2013, 46(33): 310-315. doi: 10.3182/20130918-4-JP-3022.00054 [15] Bleier M, van der Lucht J, Nüchter A. Scout3D-An underwater laser scanning system for mobile mapping[C]//The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2019, XLII-2-W18: 13-18. [16] 杨宇. 水下多通道真彩色三维重建与颜色还原方法研究[D]. 中国海洋大学, 2014. Yang Yu. Research on underwater multi-channel true color 3D reconstruction and color restoration [D]. Qingdao: Ocean Univer-sity of China, 2014. (in Chinese) [17] 徐望博. 基于结构光的河流水下地貌探测[D]. 华北水利水电大学, 2018. Xu Wangbo. Underwater geomorphic detection based on structured light [D]. Zhengzhou: North China University of Water Resources and Hydropower, 2018. (in Chinese) [18] Akkiraju N, Edelsbrunner H, Facello M, et al. Alpha shapes: definition and software[EB/OL]. (1997-10-30)[2021-09-18]. http://www.geom.uiuc.edu/. -







 下载:
下载:





















































































