空间光通信因其抗干扰能力强、通信质量高、保密性好而在国民、经济、国防科技等领域起着重要作用^[1]。与传统光束偏转技术相比，非机械光束偏转技术具有非机械调制、功耗低、轻巧灵敏等特点。非机械伺服控制的液晶空间光调制器（LCSLM）通过控制加载在每个像素上的电压能够实时调制波前相位实现光束偏转，在空间光通信中有着广泛应用，成为了信息光学系统的关键器件^[2]。

从1888年奥地利植物学家Reinitzer发现的液晶物质，到1971年美国休斯公司第一次提出基于光寻址透射式的空间光调制器，之后开始了基于液晶分子特性对光进行调制的研究^[3]。2015年，Xu等通过改变相控单元电压切换边界电场，提出了调制光波前相位的光栅模型，能实现12.1°光束偏转^[4]。国内对于液晶光束偏转技术的起步较晚，由于激光通信技术的引领，我国也逐渐加入到这种新型光束偏转技术的研究中。2013年，中国科学院光电技术研究所搭建了基于LCSLM用多片 Wollaston 棱镜扩大光束扫描的光束精偏转控制系统^[5]。2017年，长春理工大学构建了基于LCSLM实现光束的大角度扫描和连续偏转的实验系统，最大偏转角度可达4°，还能通过分光束实现对多束光单独控制^[6]。2020年，深圳光启高等理工研究院建立基于LCSLM的光束偏转和角放大光路系统，出射视场角可达91.22°^[7]。同年，电子科技大学利用改进的 GS 相位迭代算法能提高多光束偏转的衍射效率，优化光束光斑强度，降低光束的均方根误差^[8]。以上的研究有很多值得借鉴的地方，但由于基于LCSLM的各种方法可能导致光斑质量下降或偏转角度受限，基于LCSLM的光束控制技术具有很大的发展前景。

基于空间光调制器，可以应用于激光调制、波前整形、像差校正等方面，文中主要针对液晶的相位调制功能，采用反射式空间光调制器，实现对1550 nm激光的波前相位校正，基于工作原理建立模型验证了光束偏转控制能力，针对非机械高速精确的光束扫描应用设计了基于LCSLM的偏转扫描控制实验系统，根据LCSLM的可编程特性，提出了一种基于LCSLM的光波前相位调控算法，该算法可实现光束在视场范围内的任意定位，其优势是高速、精准及快捷，同时对光斑质量影响不大。光束偏转及扫描精密控制在空间光通信的目标捕获、跟踪、瞄准等这些关键技术有重要应用的价值。该控制技术无机械惯性、高分辨率、高速动态可控，还可实现同时分光束、分时多波束等应用，是目前光束控制领域最具前景的方向之一。

液晶按分子凝集构造的不同，可分为近晶相液晶、向列相液晶、胆甾相液晶三类。向列相液晶分子排列杂乱无序，不再分层，但大致以长轴方向平行排列，由于粘度小、响应速度快而最早被应用。当一束光入射到液晶面上时，会产生电控双折射效应^[9]。图1（a）为向列相液晶双折射原理图，液晶旋转时，o光的折射方向不变，e光的折射方向随着旋转方向而发生改变，在出射面重新合成的偏振态取决于o光和e光的相位差，相位差可以通过像素电压实现调控。图1（b）为到达LCSLM的入射光偏振方向与液晶分子光轴平行，此时无o光分量，加电压可以改变e光光程，从而实现对入射光相位的调控。

图  1  (a) 向列相液晶双折射原理图；(b) 相位型空间光调制器原理图

Figure 1.  (a) Schematic diagram of nematic liquid crystal birefringence; (b) Schematic diagram of phase spatial light modulator

空间光调制器是一种体积小、质量轻、数字化可编程的衍射光学元件，主要由上下平行的两个电极板和夹在电极板之间的液晶层组成，利用液晶的电控双折射效应，通过改变非寻常光折射率来调制光波前相位^[10]。文中使用LCSLM的像素数为1920×1080。下文利用菲涅耳透镜和闪耀光栅对光束的作用，通过改变LCSLM上所加载的对应模型相位图，进行了理论分析与实验验证，实现了光束分别在焦深和二维平面的移动。

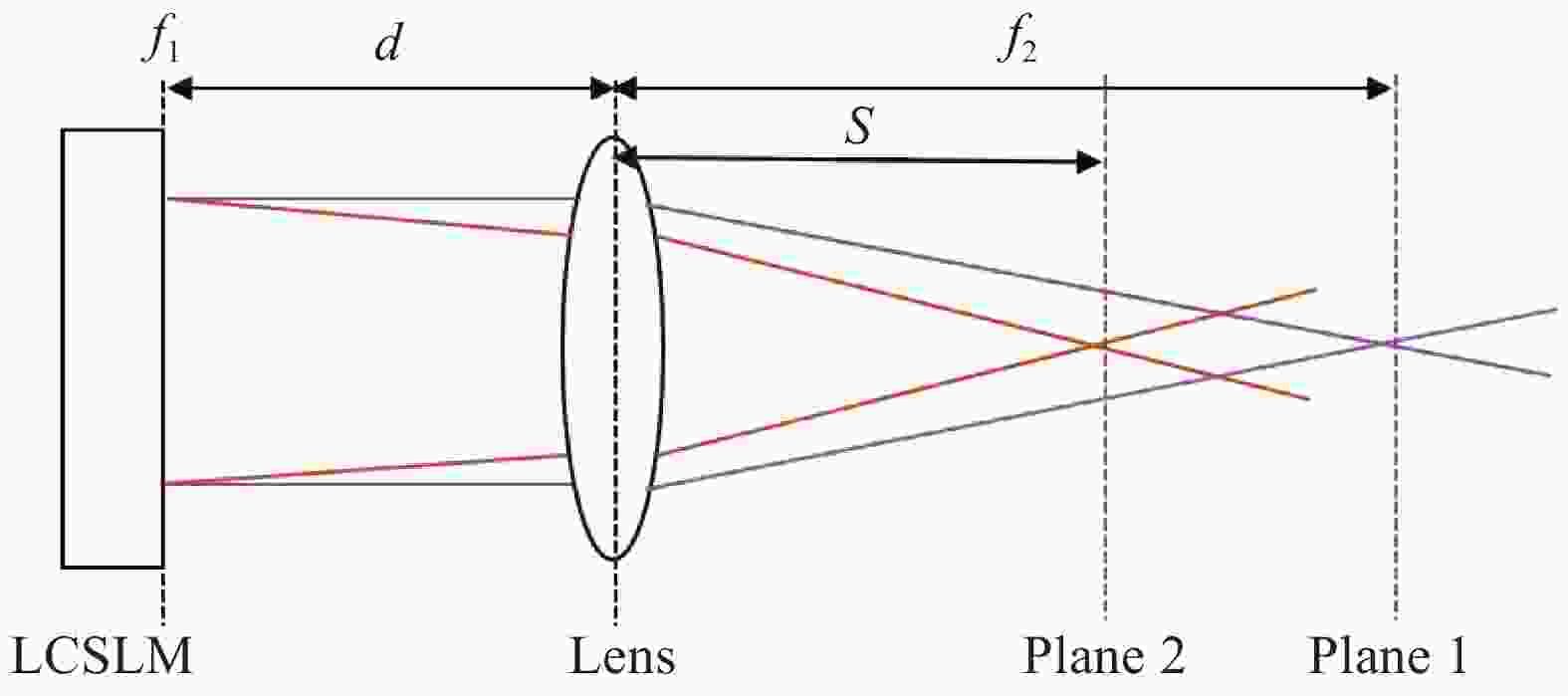
菲涅耳透镜与传统的球面透镜相比，具有更大的孔径、焦距短、材料用量更少、质量和体积更小的特点。平面波经过菲涅耳透镜后会形成会聚或发散的球面波，在中心轴上产生不同位置的焦点^[11]。叠加菲涅耳透镜相位之后，衍射的图像会沿着光轴方向前后移动，对系统的焦距影响如图2所示。

图  2  叠加菲涅耳透镜系统焦距图

Figure 2.  Superimposed Fresnel lens system focal length map

叠加菲涅耳透镜的相位对系统焦距的影响用以下公式描述。d为LCSLM到透镜的距离；f₁为LCSLM上叠加的菲涅耳透镜的焦距； f₂为普通球面透镜的焦距，即原本平行入射光通过透镜的焦距，则这两者的组合焦距为：

则第二透镜到组合系统后焦点的距离后焦距S，即叠加菲涅耳透镜之后的会聚光束的焦深位置可表示为：

叠加一个菲涅耳透镜相位，原本平行入射的光变为会聚或发散的光，经过透镜聚焦到正常焦点的前方或后方。图3(a)为菲涅耳透镜相位图，在LCSLM上加载不同焦距的菲涅耳透镜相位图进行实验，利用CCD观察到光斑的中心位置如图3(b)~(e)所示。

图  3  (a) 焦距400 mm菲涅耳透镜相位图； (b) 初始光斑；(c) 焦距200 mm光斑；(d) 焦距300 mm光斑；(e) 焦距400 mm光斑

Figure 3.  (a) Phase diagram of a Fresnel lens with a focal length of 400 mm; (b) Initial spot; (c) A spot with a focal length of 200 mm; (d) A spot with a focal length of 300 mm; (e) A spot with a focal length of 400 mm

从实验结果可以看出，施加菲涅耳相位图可以实现光束会聚的功能，改变焦距，在焦平面可以观察在焦深方向（Z轴）移动的光斑，而X、Y方向的坐标不变，图中光斑坐标均为(0,0)。而光斑大小不同可能是菲涅耳透镜的边缘作用以及在系统测量过程中产生的误差。

当对LCSLM的各个电极施加不同的电场时，液晶的指向朝着电场方向倾斜，液晶面板上呈线阵型排列的N个像素单元的折射率n_e发生变化，施加倾斜的相位延迟即可改变光束的出射方向，因此LCSLM调制光波前的2π相位变化量等效于周期性阶梯型的闪耀光栅分布^[12]。

对于m级衍射光，像素尺寸为D时，光束偏转角的推算公式为：

闪耀光栅能量大部分都分布在一级衍射上，m=2时，会同时在±1两级衍射级发生闪耀，两级衍射光强相等。m为其他值时，都是在+1衍射级发生闪耀，随着m的增大，衍射位置逐渐靠近衍射零级，由光束偏转角推导公式可知，λ、D一般不变，液晶光束偏转角主要取决于单个周期内液晶像素单元数量，m越大，光束偏转角越小。

当光正入射到LCSLM上，带有调制信息的出射光经透镜聚焦在接受面上，如图4所示，通过相位调制实现在二维平面X-Y方向偏转，汇聚点坐标为($ {x_1},{y_1} $)，出射光束的偏转角度为($ {\theta _x},{\theta _y} $)。

图  4  LCSLM调制的光束偏转角度图

Figure 4.  Diagram of LCSLM modulated beam deflection angle

其中：

θ较小时，光斑偏移距离与光栅周期之间的关系可用公式（5）表示：

式中：$ {x_0} $为光栅周期为像素尺寸D时的偏移距离。

基于闪耀光栅的光束偏转实验，设计了如图5所示的系统结构图。光源经过扩束准直后，经偏振镜变为水平线偏振光后入射至分光棱镜，经反射垂直入射至LCSLM的液晶面板上进行光束偏转调制，调制后的光束出射光经过BS通过透镜汇聚于CCD来观察和测量光斑。

图  5  基于闪耀光栅系统结构图

Figure 5.  Structure diagram based on blazed grating system

根据LCSLM的相位调制特性计算出相应的相位灰度驱动图，每个像素上的不同灰度值即可改变不同像素上的相位延迟量，通过控制软件，将生成的不同相位图加载在LCSLM上进行实验，在接收屏可以观察到如图6所示的结果。改变闪耀光栅的衍射角度、旋转角度等参数，可以看到光斑发生明显偏移。

图  6  不同衍射角度的光斑图。 (a) 初始光斑坐标(3887 μm, 2745 μm )；(b) $ {\theta _x} $=0.2 坐标(4807 μm, 2742 μm )；(c) $ {\theta _x} $=0.3 坐标(5305 μm, 2709 μm)；(d) $ {\theta _x} $=0.5 坐标(6165 μm, 2727 μm)；

Figure 6.  Spot patterns with different diffraction angles. (a) Initial spot coordinates (3887 μm, 2745 μm); (b) $ {\theta _x} $=0.2 coordinates (4807 μm, 2742 μm); (c) $ {\theta _x} $=0.3 coordinates (5305 μm, 2709 μm); (d) $ {\theta _x} $=0.5 coordinates (6165 μm, 2727 μm)

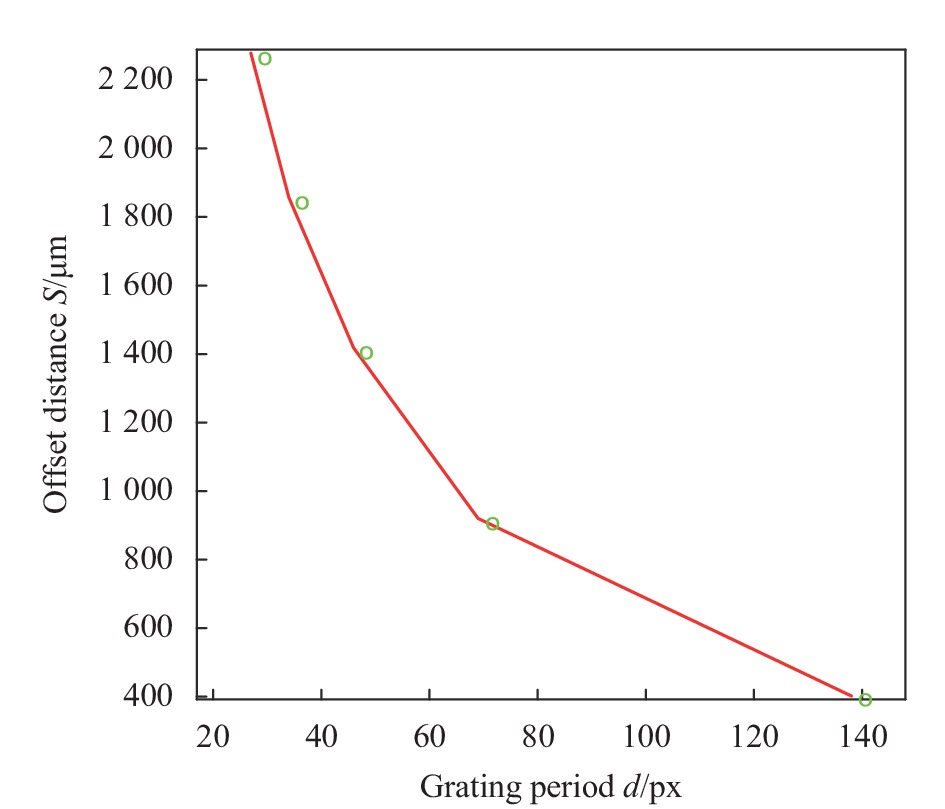
从实验结果可以看出，衍射角度越大，0~2π变化周期越多，光栅周期越小，光斑偏移距离越大，与前面的理论分析结论一致，且表现在水平方向平移。零级光来自于像素间隔的反射以及LCSLM表面玻璃的反射，不被相位调制，所以原始光斑有很弱的一部分没有被调制。光栅方程满足关系：$ d\sin \theta = \lambda $，其中λ为波长，表1是实测偏移距离S与光栅周期d之间的关系，其中单个像素大小D=6.4 μm。

将表1中的光栅周期d作为X轴，偏移距离S作为Y轴，画出的偏移距离与光栅周期之间的关系曲线如图7所示，可以看出，随着光栅周期的增多，偏移距离逐渐减小。

图  7  光斑偏移距离与光栅周期的关系

Figure 7.  Relationship between the spot offset distance and the grating period

LCSLM对于单一方向(X轴或Y轴)可实现的最大偏转角度为$ {\theta _{\max }} $：

式中：$ {d_{pix}} $为单个像素的大小^[7]。

LCSLM对于单一方向(X轴或Y轴)可实现的最小偏转角度为$ {\theta _{\min x}} $和$ {\theta _{\min y}} $：

式中：$ {d_{SLMx}} $和$ {d_{SLMy}} $为有效工作区域的边长。

入射波长为1550 nm，经计算单一方向可实现的最大偏转角度为6.96°(±3.48°)，X、Y方向的偏转精度分别为0.0073°和0.0129°。实验中光斑分析仪距离光路出射端为260 mm，X、Y方向都实现了0~±0.5°的光束偏转。当衍射角度恒为0.5°时，改变相位图的旋转角度，出射光斑结果如图8所示。

图  8  出射光斑及相位灰度图。 (a) 初始光斑坐标(6165 μm，2727 μm)；(b) 旋转角度45°光斑坐标(5497 μm，4303 μm )；(c) 旋转角度90°光斑坐标(3909 μm，4978 μm)

Figure 8.  Outgoing spot and phase gray scale map. (a) Initial spot coordinates (6165 μm, 2727 μm); (b) 45° rotation angle spot coordinates (5497 μm, 4303 μm); (c) Rotation angle 90° spot coordinates (3909 μm, 4978 μm)

从实验结果可以看出，衍射角度一定时，改变相位图的旋转角度，可以使光斑在二维平面x-y偏移。这些实验现象与理论预测一致，验证了LCSLM的相位校正能力。从实验结果可以看出除了本身的偏移点外，还会有很弱的镜像点存在，这是因为闪耀光栅本身的结构导致的，衍射角度变大时，±1级的衍射点越弱，衍射效率就越低。后续若闪耀光栅叠加菲涅耳透镜模型可以实现光束在三维方向的偏转。

主光路为光束通过透镜聚焦在CCD平面形成光斑，从CCD的光斑推导透镜前的相位。从点光源($ {x_0},{y_0} $)发出的光，其波面表现为球面波，发散球面波在与点光源相距为z的x-y平面上产生的复振幅为：

式中：${{{a}}_0}$为点源自身的振幅；$ k = 2\pi /\lambda $代表波矢。透镜将发散的球面波变换成一个会聚的球面波，根据前后变换的光场分布及高斯公式，焦距为f透镜的相位变换因子可表示为：

根据公式(8)和公式(9)可得透镜前的光场分布为：

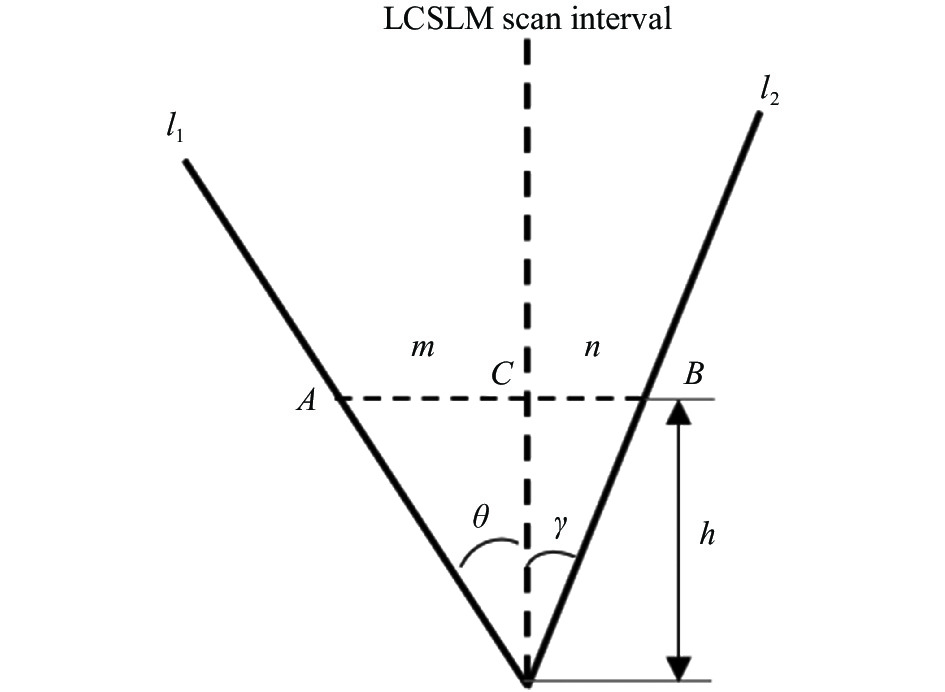
利用编程语句提取透镜前光场相位$ \varphi $，若偏移到接收视场中心位置，则在2π范围内需要补偿相位为$ 2\pi {\text{ - }}\varphi $。若要偏移到接收视场任意位置，图9所示为一维方向上相位变换模型。

图  9  相位变换模型

Figure 9.  Phase shift model

式中：$ {l_1} $为变换前相位分布；$ {l_2} $为变换后相位分布。相应变换点为A、B，根据公式(4)可知$ ({\theta _x},{\theta _y}) $，LCSLM的像素坐标$ ({x_h},{y_h}) $，根据最后想要定位到CCD上的坐标，同理可知 $ ({\gamma _x},{\gamma _y}) $，所以AC间距离m，BC间距离n可表示为：

LCSLM上每个像素对应的相位为：

0~255灰度与相位呈线性关系：

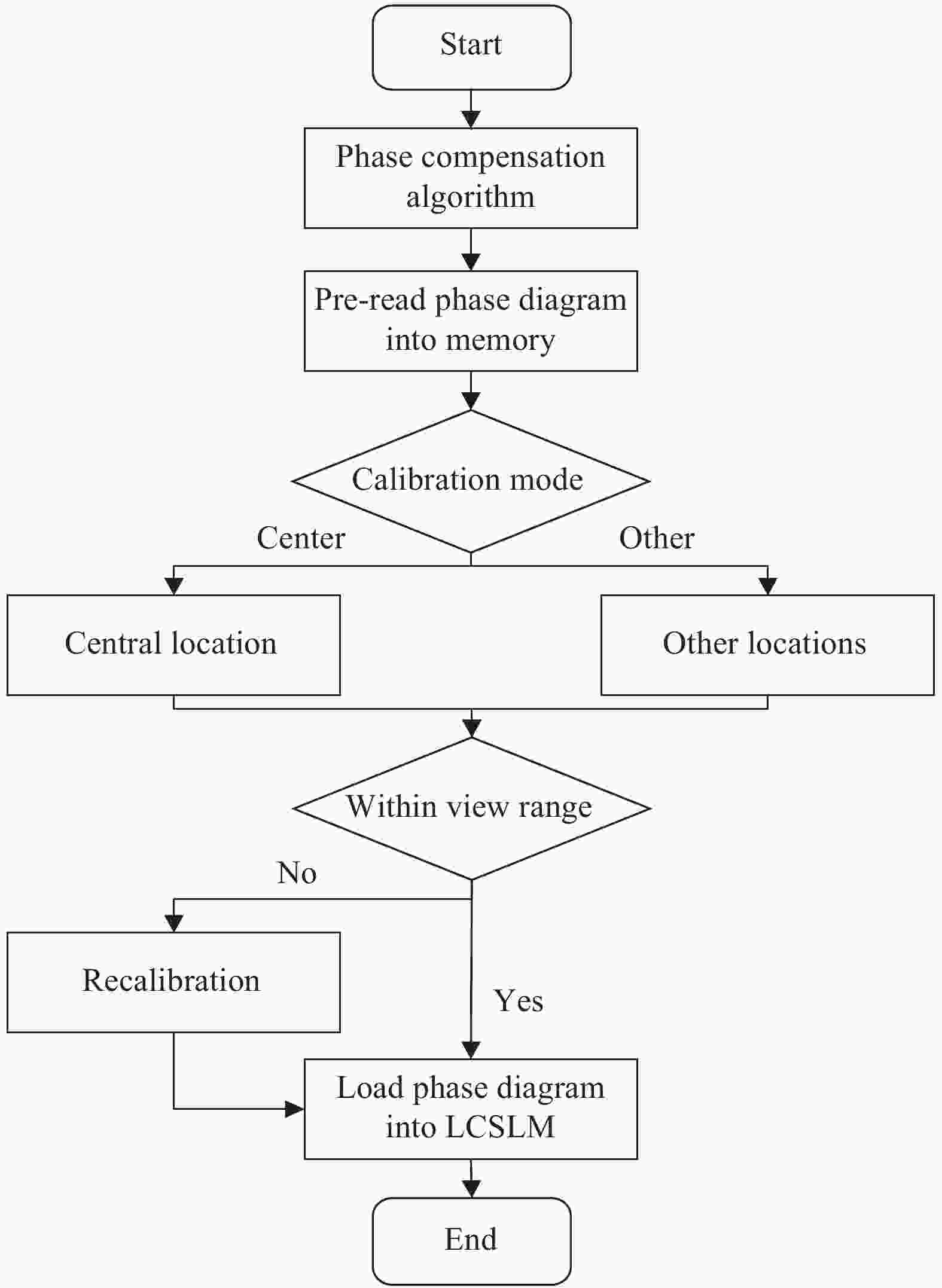
根据以上算法得到对应的相位灰度图加载在LCSLM上对光束进行偏移控制，具体的光束控制流程如图10所示。首先把预先生成的相位图预读入内存，随时调用。选择偏移模式，包括偏移到光场中心位置或360°范围内其他位置，如果在视场范围内，则加载相位图到LCSLM上，否则重新校正偏移。

图  10  光束控制流程图

Figure 10.  Flow chart of beam control

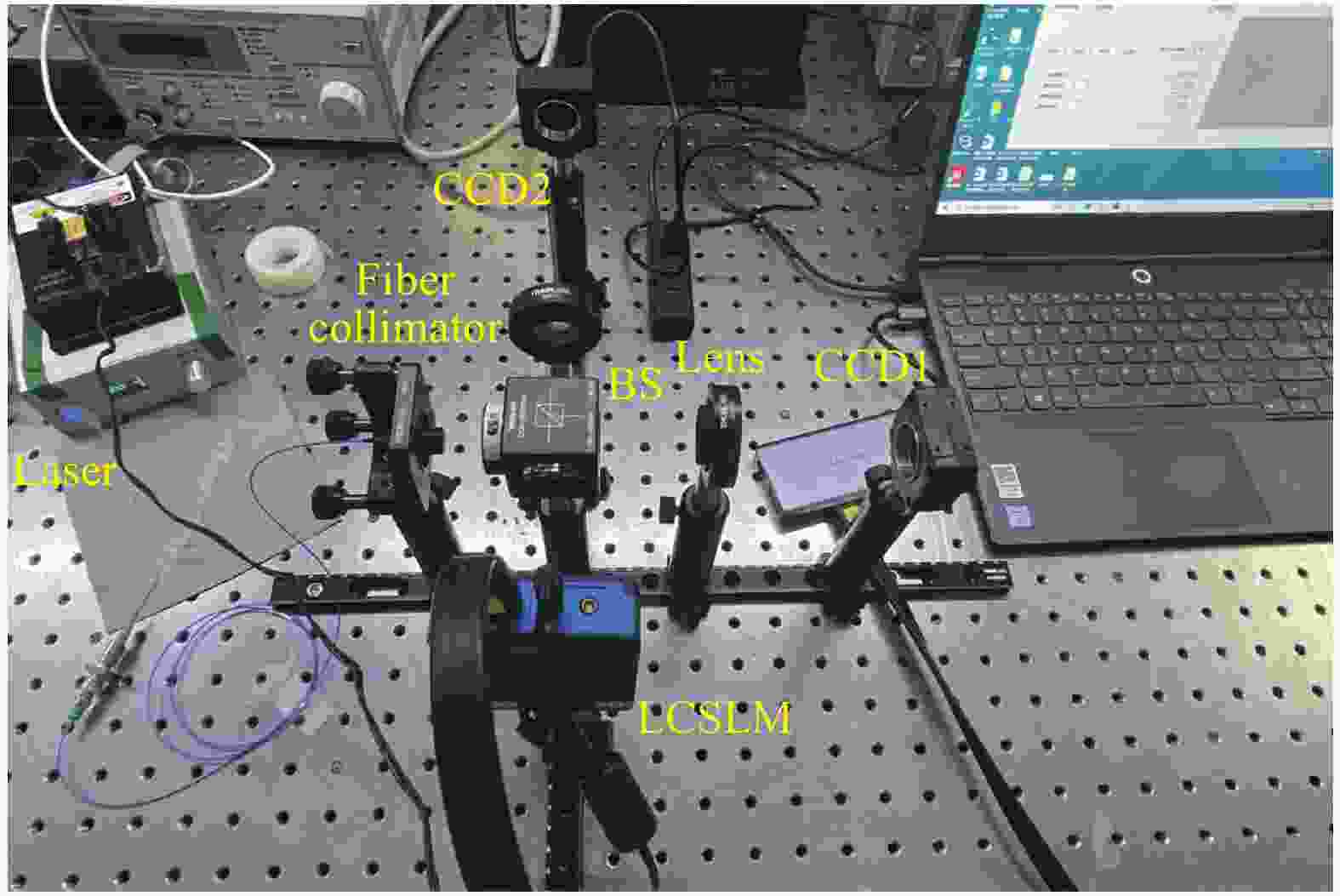
为了验证基于LCSLM高速灵活的光束偏转能力，设计空间光束偏转控制实验系统，在室内搭建实验平台，如图11所示，测试系统主要由激光器、光纤准直器、起偏器、空间光调制器、分光棱镜、CCD相机等构成。采用1550 nm的激光经过准直器扩束准直，使入射激光尽可能接近平行光，并能充满液晶靶面，扩束后的光束入射到偏振片变为水平线偏振光，再经分光棱镜被分成两束光路，一束光经透镜聚焦到CCD1而得知光斑坐标，另一束反射光垂直入射到SLM上，根据光斑坐标反推透镜前相位，通过计算机控制软件来补偿光波前相位，从而改变出射光的位置。经SLM反射的出射光经过BS入射到CCD2一路接收来观察和测量光斑。

图  11  实验实物图

Figure 11.  Physical image of the experiment

根据CCD1成像一路的坐标位置和透镜的相位变换作用，根据LCSLM液晶屏的大小确定扫描面范围，反推透镜之前的光场并提取光场相位分布，通过LCSLM补偿该相位改变等相位面为垂直方向，使光斑偏移到光场的中心位置。

根据CCD1接收的光斑坐标分别为(1.050 mm,0.188 mm)、(−1.313 mm, −0.938 mm)、(0.938 mm, −1.125 mm)，推导透镜之前的光束相位分布，补偿该相位得到的灰度值分布及其灰度相位图如图12所示，其中只展示坐标为(1.050 mm, 0.188 mm)的补偿相位图。

图  12  (a) 1920×1080 pixel灰度值分布； (b) LCSLM灰度相位图

Figure 12.  (a) 1920×1080 pixel gray value distribution; (b) LCSLM grayscale phase map

经LCSLM调制，使用相同的两个CCD相机标定，通过加载补偿的相位图，任意位置的光斑都可偏移到光场中心位置，在另一路CCD2观察光斑如图13所示。

图  13  (a) 初始光斑坐标(1.050 mm, 0.188 mm)；(b) 初始光斑坐标(−1.313 mm, −0.938 mm)； (c) 初始光斑坐标(0.938 mm, −1.125 mm) ；(d)~(f) 调制后光斑坐标(0,0)

Figure 13.  (a) Initial spot coordinates (1.050 mm, 0.188 mm); (b) Initial spot coordinates (−1.313 mm, −0.938 mm); (c) Initial spot coordinates (0.938 mm, −1.125 mm); (d)-(f) Modulated spot coordinates (0,0)

从实验结果中可以看出， 光场中任意位置的光斑可以精确定位到中心位置，基于LCSLM的光波前相位调控算法，光斑也可以在接收视场的任意范围内偏移。此款LCSLM的光学利用率为75%左右，加上其他光学器件的损耗，偏移后的光斑能量有所下降。以60 frame/s的速率使光斑在视场范围内进行十字扫描，扫描结果如图14所示。红色标记为初始光斑位置，a~h分别为同一光束经过不同相位控制后，在光场中不同位置的汇聚结果图。

图  14  光斑十字扫描结果图

Figure 14.  Result of the cross scan of the spot

由于LCSLM的衍射效率和像素间隔的问题，光斑强度会减弱，实验中误差产生的原因主要是LCSLM像素的离散结构导致相位延迟存在偏差，此外，实验装置的光路也存在装调误差与测量误差，两路光路CCD标定不一致时，光斑偏移就会产生误差。

文中利用空间光调制器的高分辨率，单独像素寻址的高速纯相位调制作用及可编程特性，提出一种满足光束高速灵活的偏转方案。在LCSLM上分别加载菲涅耳透镜相位图和闪耀光栅相位图，可实现光束在光轴方向和二维平面的偏移。针对空间光通信中光束的高速精确的扫描技术，设计了基于LCSLM的光束偏转扫描控制实验系统，提出了基于LCSLM的光波前相位调控算法，通过补偿等相位面使任意位置的光斑可偏移定位到接收光场中心位置或其他位置，实现了LCSLM对光束灵活偏转控制的能力。后续应优化相位图算法，能够实现自适应实时控制光束。