下载:
-
成像光学系统在国防、科教、医疗等领域应用广泛。在空间相机[1]、红外侦察[2]、头盔显示器[3]、仿生复眼[4]、水下成像[5]、成像光谱仪[6]、极紫外光刻物镜[7]等仪器设备中，成像光学系统作为其核心组件，承担收集能量及信息的重要任务。在保证成像质量的前提下，光学系统朝着大视场、大孔径、宽波段、无遮拦、轻量化的方向进一步发展[8]。随着成像光学系统各项设计指标的提升，球面、二次曲面以及各类非球面等传统面型已无法满足先进成像光学系统的设计需求。与此同时，加工[9]和检测技术[10]的飞速发展为自由曲面在成像光学系统中的应用创造了条件。
光学自由曲面一般是指相对于光轴而言不具备旋转对称特性的面型[11]。自由曲面的面型表征中变量参数较多，使其可以精准地调控光线的方向和角度，像差校正能力强[12]，在系统中也承担更多的平衡像差的任务。因此相较于传统的旋转对称面型，应用自由曲面的成像光学系统具有更高的设计自由度，更易实现系统小型化、轻量化的设计目标。
不同于传统同轴光学系统各元件以光轴为中心的排布方式，自由曲面成像光学系统中各元件的空间布局方式更加灵活。在相同的设计参数下，不同的结构形式也会影响到自由曲面对离轴像差的校正能力，不合理的结构选型会令各自由曲面的像差校正效果相互抵消，降低设计效率，也限制了像质的进一步提升[13]。过去，国内外在同轴光学系统的设计研究方面投入时间长、像差理论系统完备、成果丰富、可借鉴的初始结构种类多；自由曲面光学是近些年光学设计领域的前沿问题之一，可借鉴的初始结构数量少。没有完备像差理论指导的初始结构不一定具有足够的像差校正能力，设计效率低。因此，对于自由曲面成像光学系统而言，初始结构的设计至关重要。
文中对现有的自由曲面成像光学系统的初始结构设计方法进行分类、归纳和总结，依据初始结构设计原理将其分为同轴系统离轴化法、直接设计法、视场孔径扩展法和分段拼接融合设计方法，对各类设计方法的特点进行详细阐述。最后，文中分析总结了自由曲面成像光学系统的初始结构设计中亟待解决的问题，并对未来的发展方向进行了讨论与展望。
-
反射式或折反射式自由曲面成像光学系统初始结构构建的一个经典思路是从近轴光学理论出发，基于初级像差理论求解同轴系统结构参数，再通过视场离轴或孔径偏心的方式消除系统中的光线遮拦，完成初始结构的建立[14]。离轴化为各元件的空间布局提供了更多的可能性，但系统的结构型式、自由曲面面型的选取都会影响系统最终的成像性能。另外，在自由曲面成像光学系统初始结构设计的过程中还需要考虑对各元件空间布局的约束，以避免在后续优化过程中各元件之间的干扰。
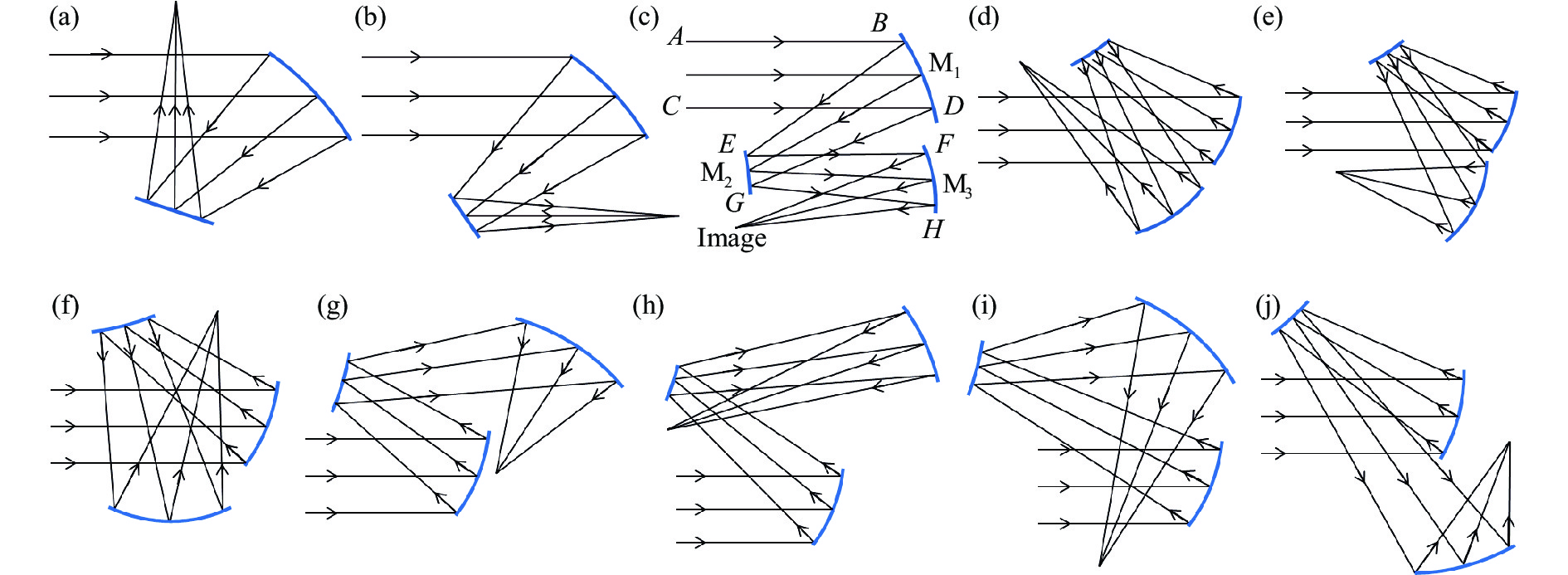
基于初级像差理论可以初步确定同轴系统中各元件光焦度，而后调整各元件的旋转角度及离轴量确定空间布局，实现系统的离轴化。失去光轴的约束后，系统的布局型式丰富，离轴两反成像系统有4型和Z型两种结构型式，分别如图1 (a)、 (b)所示；离轴三反成像系统由于镜片数量和设计参数的增多，结构型式更为多样，以光焦度按正-负-正分配的离轴三反为例，有八种空间布局方案，如图1 (c)~(j)所示。在离轴化的过程中，原有节点像差特性被破坏，同时引入彗差、像散等离轴像差，而结构型式决定了系统对离轴像差的校正能力。对于两反系统，Z型结构在实现大视场成像方面更具优势但占用的空间大，而对于小F数系统4型结构与Z型结构在像质上差别不大，但4型结构布局紧凑、体积小[15]；对于离轴三反系统，在相同的设计指标下，图1 (c)所示的结构更容易设计，得到高像质的成像光学系统，相比而言图1 (d)～(g)在提高像质方面没有明显的优势，但是各元件间结构紧凑，占用空间位置小，而图1 (h)～(j)所示的结构在后续设计中对像差的校正能力远不及上述三种结构[13]。设计者需要针对成像清晰度、体积质量等设计指标平衡各类设计指标需求，选取最合理的布局型式，避免由于结构选型不合理导致各自由曲面的像差校正能力相互抵消，降低设计效率。
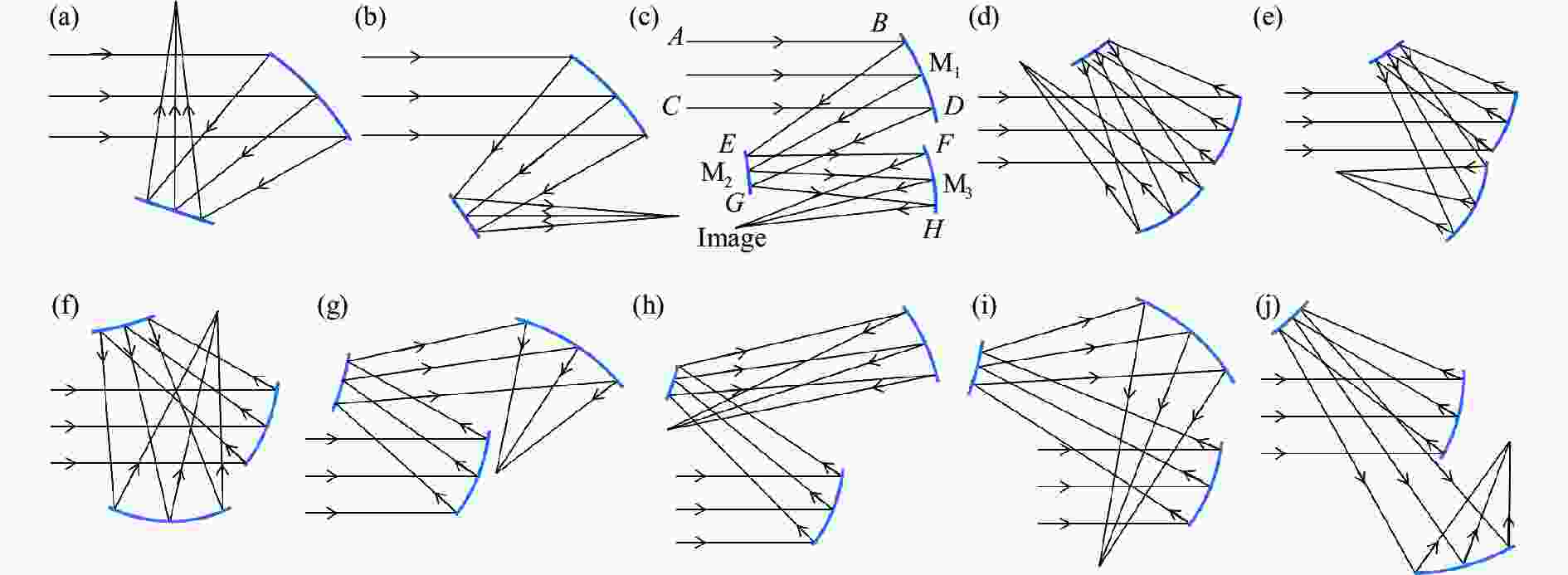
图 1 离轴化的不同结构型式。(a) 4型结构的离轴两反系统； (b) Z型结构的离轴两反系统； (c)~(j)离轴三反系统的八种结构型式
Figure 1. Different off-axis structures. (a) 4-type structure off-axis two-reflective system; (b) Z-type structure two-reflective system; (c)-(j) Eight structural types of off-axis three-reflective system
除此之外，自由曲面的位置、数量以及表征方式也是影响自由曲面光学系统设计效率和成像质量的关键因素。尽管自由曲面具有诸多优势，但在成像光学系统中采用过多的自由曲面或表征多项式数量过多都有可能在后续优化设计过程中限制像质的进一步提升。不同于同轴光学系统，离轴光学系统中旋转对称特性被破坏，像差场分布与元件的倾斜程度紧密相关，位置不同的面作为自由曲面对成像产生的影响可能大相径庭。因此，在构建自由曲面成像光学系统初始结构时，需要根据设计需求灵活地选取自由曲面及其表征形式。
通过同轴系统离轴化的方法得到的初始结构在后续优化过程中难以避免各个元件分布向同轴化逼近的趋势，因此在优化之前需要根据光线的走向对各元件旋转角度及离轴量进行约束。以图1 (c)中所示的离轴三反结构为例，对其元件空间布局的约束如下：
(1) 入射到M1下边缘的光线CD高于M2的上边缘点E；
(2) M3的上边缘点F不得高于光线CD；
(3) 像面不得高于光线GH。
在后续优化设计的过程中基于上述约束条件对系统进行优化调整，在进一步提升像质的同时避免各元件趋于同轴而导致的光线遮拦问题。
该方法是早期自由曲面光学系统的初始结构设计常用方法，虽然在同轴结构的求解过程中，对系统的球差、彗差、场曲和像散进行了控制，但是光学元件的偏心和旋转破坏了系统原本的旋转对称特性，在改变像差节点特性的同时，也引入了新的离轴像差，像差场的偏移大大降低了系统的整体性能。综上，同轴系统离轴化的初始结构设计方法基于同轴像差理论，在同轴结构的基础上调整各元件的空间位置获得初始结构，求解过程相对简单，但由离轴化引入的像差校正缺乏理论指导，初始结构的选型和构建也往往依赖于设计经验。
-
自由曲面的直接设计法是指根据成像系统设计指标中的物像关系，利用等光程等理想成像原理和折反射定律等几何光学传播定律，建立起光线与表面之间的方程组并求解得到曲面离散点数据信息，对其进行拟合得到自由曲面。常见的方法有偏微分方程法、多曲面同步设计法及逐点构建-迭代法。
-
1949年，Wasserman和E.Wolf 提出Wasserman-Wolf微分方程，用于同轴光学系统中相邻非球面面型参数的求解[16]。1957年，E.Vaskas在此基础上进一步推导，将Wasserman-Wolf微分方程的适用范围扩大至两个非相邻非球面的求解[17]。2002年，Knapp. D.J.将微分方程求解的思想应用到非旋转对称的光学系统设计中，推导出两个新的微分方程并求解，完成非旋转对称光学系统中校正板的设计[18]。2007年，Andrew Hicks 通过建立偏微分方程组构建自由曲面反射镜，实现大视场成像系统中畸变的校正[19]。2010年，北京理工大学王涌天团队利用偏微分方程法完成离轴自由曲面棱镜式头戴显示系统的设计[20]。
偏微分方程法的自由曲面面型设计思想是依据成像系统的物像关系，在已知入射光线和出射光线方向矢量的前提下，基于折反射定律建立微分方程组求解自由曲面表面矢高点坐标及其对应的法向量坐标，最后通过自由曲面表征函数对离散点进行拟合，得到自由曲面初始面型。
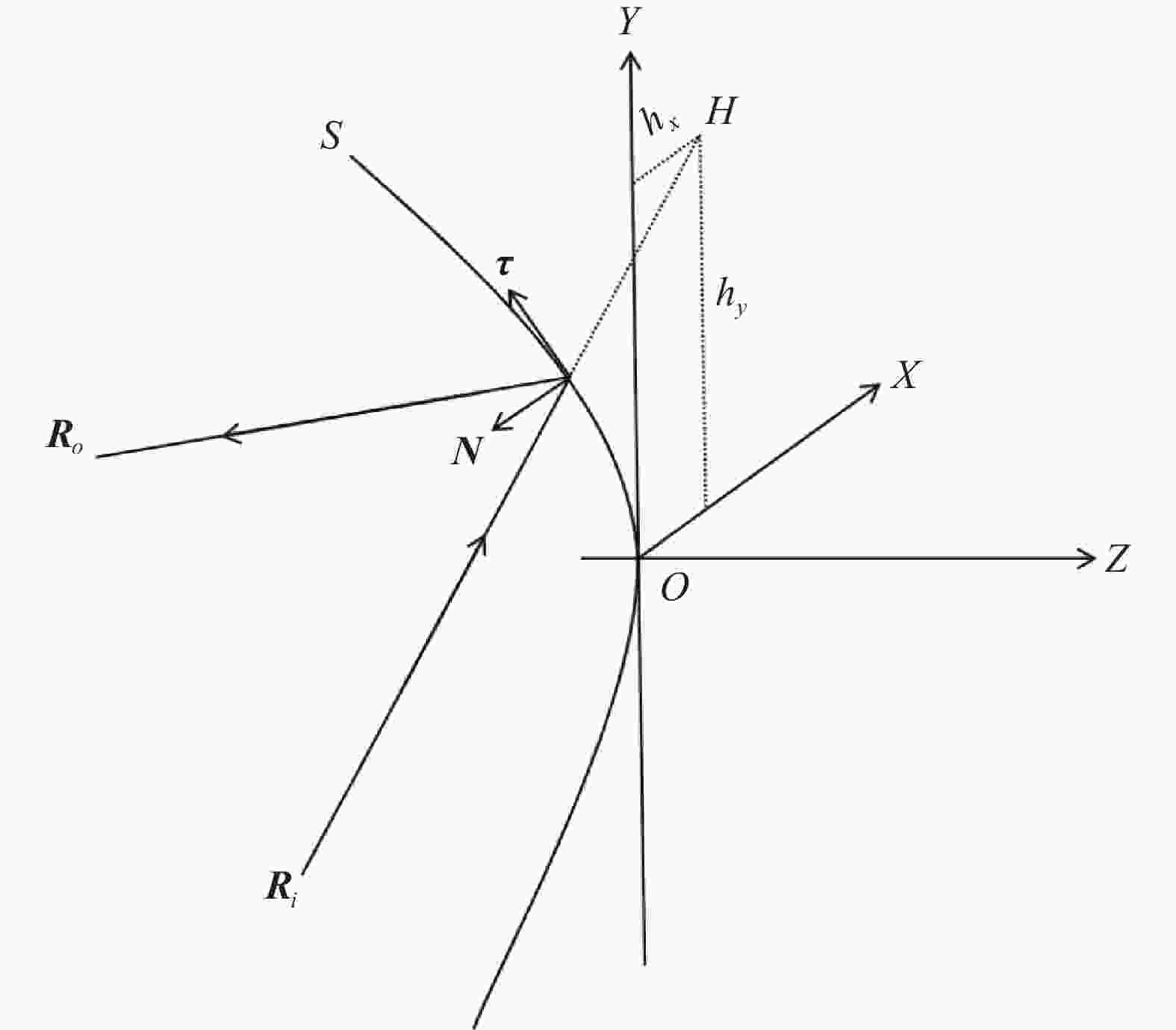
以单个自由曲面反射镜的构造为例，以自由曲面S的顶点位置为坐标原点O，建立空间直角坐标系，如图2所示。
图 2 偏微分方程法原理示意图
Figure 2. Schematic of the principle of partial differential equation method
XOY平面与自由曲面相切，待求曲面S可用参数方程表示为：
$$ \left\{ \begin{gathered} x = x(t) \\ y = y(t) \\ \textit{z} = \textit{z}(t) \\ \end{gathered} \right. $$ (1) 式中：x，y，z为曲面S上的点坐标；t为参数。入射到自由曲面的光线向量以及其对应的出射光线向量可由物像关系得到。记入射光线单位矢量为Ri (cosθix, cosθiy, cosθiz)，与其对应的出射光线单位矢量为Ro(cosθox, cosθoy, cosθoz)，入射光线所在直线与XOY平面的交点为H (hx, hy)，入射光线与自由曲面的交点处法向量为N，切向量为τ。根据向量之间的几何关系有：
$$ {\boldsymbol{N}} = \frac{{{{\boldsymbol{R}}_{\boldsymbol{o}}} - {{\boldsymbol{R}}_{\boldsymbol{i}}}}}{2} $$ (2) $$ {\boldsymbol{N}} \cdot {\boldsymbol{\tau }} = 0 $$ (3) 将公式(2)代入公式(3)可得：
$$ \frac{{{\rm d}\textit{z}}}{{{\rm d}t}} = - \frac{{\cos {\theta _{ox}} - \cos {\theta _{ix}}}}{{\cos {\theta _{o\textit{z}}} - \cos {\theta _{i\textit{z}}}}} \times \frac{{{\rm d}x}}{{{\rm d}t}} - \frac{{\cos {\theta _{oy}} - \cos {\theta _{iy}}}}{{\cos {\theta _{o\textit{z}}} - \cos {\theta _{i\textit{z}}}}} \times \frac{{{\rm d}y}}{{{\rm d}t}} $$ (4) 式中：cosθix, cosθiy , cosθiz，cosθox, cosθoy , cosθoz分别为入射光线和出射光线的方向余弦。光线与自由曲面的交点x和y坐标如公式(5)所示：
$$ \begin{gathered} x = {h_x} + \textit{z} \cdot \frac{{\cos {\theta _{ix}}}}{{\cos {\theta _{i \textit{z}}}}} \\ y = {h_y} + \textit{z} \cdot \frac{{\cos {\theta _{iy}}}}{{\cos {\theta _{i \textit{z}}}}} \\ \end{gathered} $$ (5) 式中：hx，hy为H的横纵坐标。联立公式(4)、(5)，可得：
$$ \begin{split} &\frac{{{\rm d}\textit{z}}}{{{\rm d}t}} = \left( - \frac{{\cos {\theta _{ox}} - \cos {\theta _{ix}}}}{{\cos {\theta _{oz}} - \cos {\theta _{i \textit{z}}}}} \cdot \left[\frac{{{\rm d}{h_x}}}{{{\rm d}t}} + \textit{z} \cdot \frac{{{\rm d}\left(\tan {\theta _{ix}}/\tan {\theta _{iz}}\right)}}{{{\rm d}t}}\right] -\right.\\ &\left.\frac{{\cos {\theta _{oy}} - \cos {\theta _{iy}}}}{{\cos {\theta _{o \textit{z}}} - \cos {\theta _{i \textit{z}}}}} \cdot \left[\frac{{{\rm d}{h_y}}}{{{\rm d}t}} + \textit{z} \cdot \frac{{{\rm d}(\tan {\theta _{iy}}/\tan {\theta _{i \textit{z}}})}}{{{\rm d}t}}\right]\right) \Big{/}\\ &\left(1 + \frac{{\cos {\theta _{ox}} - \cos {\theta _{ix}}}}{{\cos {\theta _{o \textit{z}}} - \cos {\theta _{i \textit{z}}}}} \cdot \frac{{\tan {\theta _{ix}}}}{{\tan {\theta _{i \textit{z}}}}} + \frac{{\cos {\theta _{oy}} - \cos {\theta _{iy}}}}{{\cos {\theta _{o \textit{z}}} - \cos {\theta _{i \textit{z}}}}} \cdot \frac{{\tan {\theta _{iy}}}}{{\tan {\theta _{i \textit{z}}}}}\right) \end{split} $$ (6) 根据物像关系建立如公式(6)所示的一系列微分方程组并求解，即可得到曲面上多个离散坐标数据点及其对应的法向量数据，对这些离散数据点集合拟合生成连续光滑的自由曲面。
偏微分方程法是构建自由曲面的一种通用方法，由于在微分方程的构建过程中只考虑对各个视场主光线方向的控制，忽略了主光线周围一定孔径内光束的像差校正，因此偏微分方程法构造的初始结构在后续设计过程中对孔径像差的校正存在局限性。
-
多曲面同步设计法(Simulataneous multiple surface, SMS)是美国LPI公司于1990年提出的一种基于等光程原理的面型构造方法[21]。该方法最初用于非成像光学系统的设计，而后经过进一步的改进和发展应用于成像光学系统的设计中。2009年，西班牙马德里理工大学的Juan C. Miñano等人应用SMS法的曲面构造思想实现了超短距投影系统的设计[22]，2012年Miñano等人基于该设计原理，推导三维空间中自由曲面的设计方法[23]。2015年，布鲁塞尔自由大学的Yunfeng Nie等人将该方法与拓展多视场的自由曲面逐点设计方法结合，完成了同轴和离轴两种结构形式的自由曲面成像系统初始结构的建立，并实现全视场内各像差的平衡[24-25]。
SMS法从理想成像的等光程原理出发，利用理想成像物像关系、光路可逆原理以及折反射定律建立方程组，可同时得到两个及以上的曲面面型。如图3所示，在对称式光学系统中，物面上边缘点O1成像至像面边缘点I1，与O1对称的物点O2成像至像面边缘点I2。由O1发出的光线R1经待求曲面S1上点P0后与待求曲面S2相交于点P1，并与像面相交于点I1。由像点I2发出光线R2，经S2上点P1后与S1相交于点P2，根据光路可逆原理，光线R2与物面相交于点O2。同理，由物点O1发出光线R3，经S1上点P2后与S2相交于点P3，并成像于I1，再由像点I2发出光线R4，经S2上点P3后，与S1相交于点P4，并成像于物点O2。
图 3 SMS法原理示意图
Figure 3. Schematic of the principle of SMS
首先，在已知P0点坐标及S1在P0处的法线向量N0的前提下，求解P1点坐标及S2在P1处的法线向量N1。P1点坐标可表示为：
$$ {P_1} = {P_0} + \left[{P_0}{P_1}\right]{{\boldsymbol{r}}_{\boldsymbol{1}}} $$ (7) 式中：[P0P1]为P0到P1的光程；r1为光线R1在S1和S2之间传播的光线方向矢量。P0到像点I1的光程可表示为：
$$ \left[{P_0}{I_1}\right] = \left[{O_1}{I_1}\right] - \left[{O_1}{P_0}\right] $$ (8) 根据折射定律设立方程，并联立公式(7)、(8)建立方程组并求解，即可得到P1点坐标及S2在P1处的法线向量N1。
同理，根据I1发出的光线R2，在已知P1点坐标及S2在P1处的法线向量N1的前提下，可建立方程组求解P2点坐标及S1在P2处的法线向量N2。重复上述过程，可以求解得到一系列离散点坐标Pi及其对应的法线向量Ni。对离散点P2n拟合可得到自由曲面S1的初始面型，对离散点P2n+1进行拟合可得到自由曲面S2的初始面型。
SMS法可同时计算求解多个自由曲面面型，但其求解过程复杂。求解的曲面个数与选取的物像关系数量一致，计算两对物像关系可求解两个曲面面型，计算四对物像关系可求解四个曲面面型。由于计算采样的物像关系数量有限，因此自由曲面的拟合精度受到离散数据点数据量的影响。
-
2013年，清华大学朱钧课题组提出一种基于逐点构建与迭代的二维自由曲面设计方法(CI-2D)[26]。该方法以平面或简单曲面作为初始面型，通过特征光线的追迹得到曲面上若干个特征数据点，再经多次迭代进一步优化自由曲面面型，得到成像光学系统的初始结构。
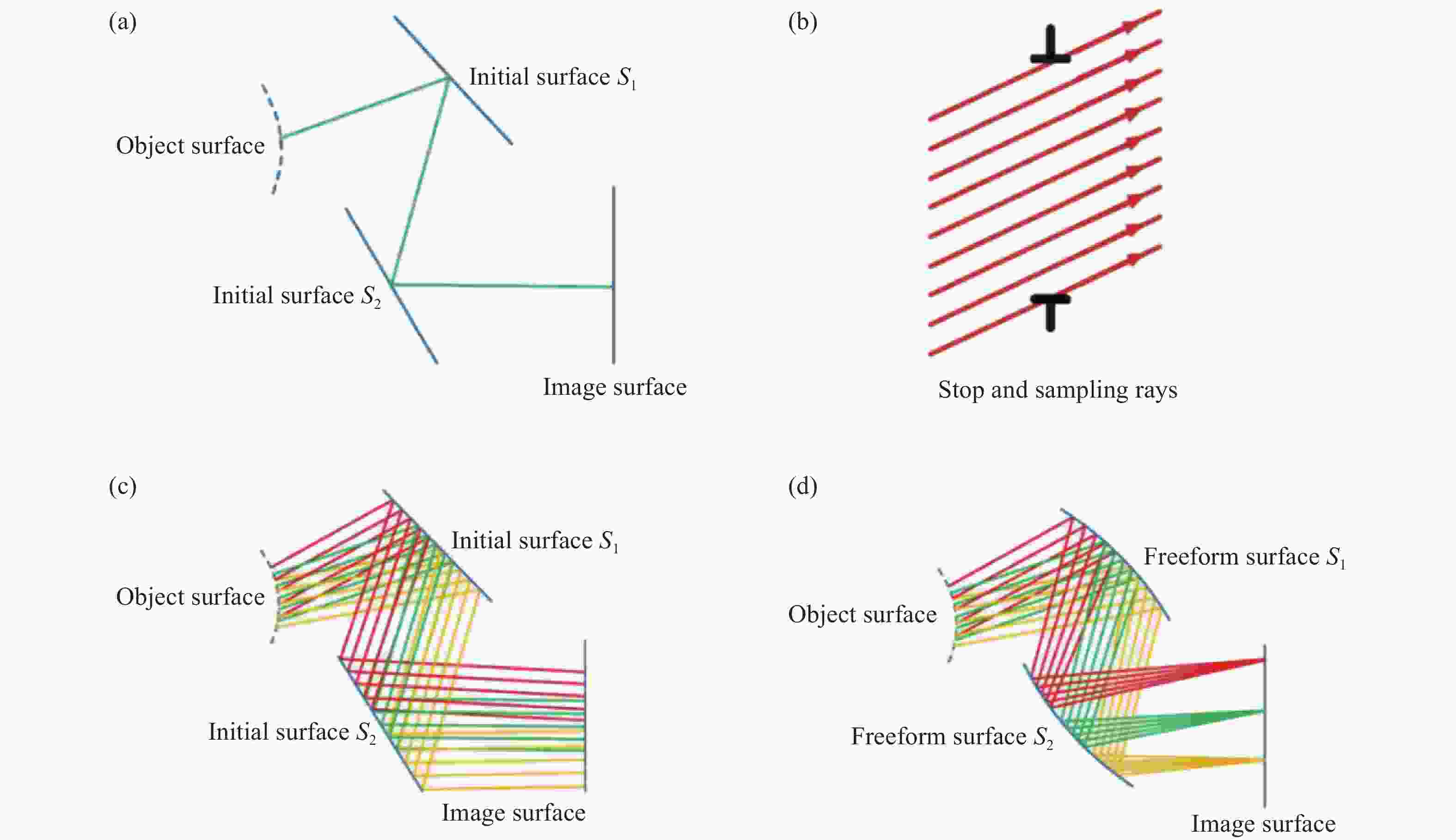
图4所示为CI-2D法设计初始结构的原理示意图[27]。首先根据物像关系及设计需求，用平面或简单曲面作为初始面型初步确定各元件的空间布局和相对位置关系；接着选取特征光线，在极坐标下对多个视场和不同光瞳坐标的光线进行采样并追迹；然后依据待求曲面上入射光线和出射光线之间的关系，通过折反射定律计算求解曲面上离散点坐标及其对应的法线向量；最后对一系列离散点及其法向量进行拟合，完成自由曲面的逐点构建过程。再将构建得到的曲面作为初始曲面，重复上述构建过程，通过多次迭代，使采样光线与待求面型的交点和期望目标点之间的偏差进一步缩小，进而实现从简单平面出发的自由曲面成像光学系统初始结构构建。
2014年，朱钧课题组将逐点构建-迭代这一设计思想进一步拓展至三维空间自由曲面的构建，并改进了逐点求解离散点的计算方法[28-29]。同年，该课题组提出兼顾表面离散点数据坐标和法向量的高精度自由曲面拟合方法[30]。在此基础上，该课题组完成了多个离轴反射式自由曲面成像光学系统的设计[28-29, 31]。2017年，该课题组将逐点构建-迭代的设计思想与神经网络机器学习相结合，只需依据设计需求给定参数以及平面元件的空间布局位置，即可实现从平面结构到自由曲面成像光学系统的初始结构自动设计[32]。
综上，逐点构建-迭代的初始结构构造方法以平面或简单曲面作为设计起点，是一种巧妙的初始结构设计方法，实现了自由曲面光学系统初始结构“从无到有”的建立。这种直接设计方法的构造过程也与光学系统几何特性及像差校正关联性不大。
-
直接设计法的本质是建立起小视场、小相对孔径自由曲面光学系统的初始结构，此节讨论的视场孔径扩展法则是从前人的设计成果中，找到小视场、小相对孔径的自由曲面光学系统初始结构，而后基于面型多项式与视场像差、孔径像差的关联性，逐步增加参与优化的关联多项式，同时扩大系统的设计孔径与视场，得到大视场或大相对孔径的自由曲面光学系统的初始结构。
视场孔径扩展法是2018年南京理工大学高志山团队提出的一种针对离轴反射式系统的初始结构设计及优化方法[33]。该方法以小视场系统为起点，通过分析波像差，在设计过程中有针对性地构造曲面校正像差，同时将面型优化与视场扩展相结合，实现全视场自由曲面光学系统初始结构的设计，该类方法充分继承了经典结构在像差校正能力方面的研究成果。基于这一设计思想，高志山团队完成了视场为 30°×3°的离轴三反光学系统设计[34]。
面型优化策略以像差平衡原理为核心指导思想，根据出射波前分析系统像差分布情况，以系数平方和较大的Zernike项对应像差优先校正原则，确定像差的优化顺序，在自由曲面上叠加指定像差成分，与原有结构中像差相平衡，从而达到提高成像质量的目的。视场扩展策略对全视场按照X方向和Y方向进行划分，并分别选取相应的步长进行拓展，如图5所示。拓展步长的设置会影响迭代优化的次数，选取步长过小，会增加视场扩展次数，降低设计效率；步长过大则加大优化难度，难以获得理想成像质量。
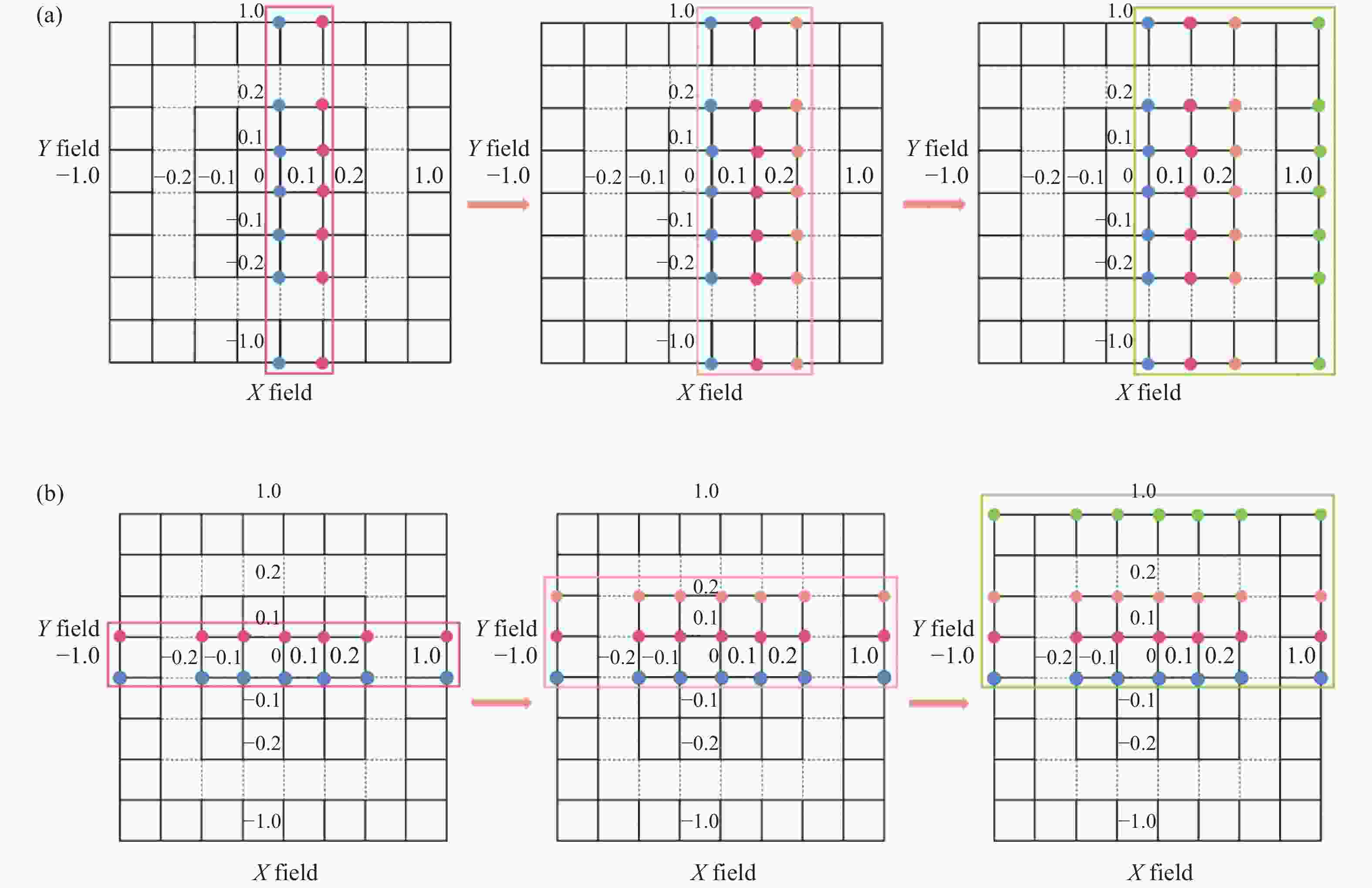
图 5 视场扩展示意图。 (a) X方向视场扩展； (b) Y方向视场扩展
Figure 5. Schematic of expending FOV. (a) Expanding the FOV in the X; (b) Expanding the FOV in the Y
在自由曲面构造和初始结构设计的过程中，面型优化与视场扩展策略同步交替进行，流程图如图6所示。以小视场离轴反射式光学系统为设计起点，根据面型优化策略，计算系数平方和最大项对应的Zernike项Zk，将其设置为优化变量；同时根据视场优化策略，求解各视场波像差在总视场波像差中的占比，令其比值为对应视场的优化权重。在确定优化变量以及各视场优化权重后进行一轮优化，若优化后仍无法满足当前设计需求，则按照像差优先校正原则令下一个系数平方和最大项对应的Zernike项为新的Zk。重复迭代上述过程，直至系统满足设计指标要求。
图 6 基于自由曲面的交替优化方法流程图
Figure 6. Flow chart of alternate optimization method based on freeform surface
该方法是在自由曲面多参数优化法的基础上衍生出的一种交替对面型和视场进行优化的自由曲面设计方法。2019年，中国科学院长春光学精密机械与物理研究所孟庆宇等人应用类似的设计思想实现了80°×4° 的超宽视场离轴三反成像光学系统的设计[35]。该方法在设计过程中，通过分析系统波像差成分指导自由曲面的构建，求解过程简单、优化效率高，同时弥补了多参数优化法不具备像差针对性的缺陷，可用于大视场自由曲面成像光学系统初始结构的设计。
-
一直以来，圆锥曲面凭借其特有的良好成像特性及简洁的面型表征方式，被广泛应用于成像光学系统的设计中。椭球面可对位于其焦点处的点物完善成像(实像)于另一焦点位置；抛物面可对无穷远物成完善像于焦点位置；而双曲面可对位于其焦点处的点物成完善虚像于另一焦点位置[36]。
理想的自由曲面成像系统必定对任意视场的点物成完善点像，若将系统的面视场分解为一系列视场点，则对任一视场点，可通过自由曲面上的某一区域实现完善成像，基于这样的分段拼接融合法充分利用圆锥曲面完善成像的光学特性，并在此基础上构造自由曲面面型，完成自由曲面成像光学系统初始结构的构建。
-
椭球面的两个焦点为一对完善成像共轭点，如图7 (a)所示，当物位于焦点F1处时，F1发出的所有光线经椭球内壁反射后都会聚焦于像点F2，利用椭球面的这种光学特性，构造出的双椭球结构如图7 (b)所示，物点位于椭球面1的焦点F1位置，物点发出的光线经过椭球1反射后会聚于焦点F2处，F2同时也是椭球2的一个焦点，最终所有光线在椭球面2的焦点同时也是理想像点F3处会聚。2013年，中国科学院长春光学精密机械与物理研究所杨建明等人提出利用双椭球面反射镜实现广角、轻量化的无失真头戴显示系统，如图7 (c)所示，但由于实际光线存在一定的孔径，因此在系统中加入了中继镜组用于补偿失真、校正像差。最终该系统实现了单通道视场120°×120°，双目视场160°×120°，重叠视场80°的头戴显示系统的设计[37]。
另外，2010年，美国中佛罗里达大学的F.Fournier基于光源和目标面等照度网格的映射关系，利用椭球面对点物成完善点像的光学特性，结合偏微分方程组，求解椭球面结构参数，而后通过对多个椭球面的拼接融合构造自由曲面，最终完成了单反射器的设计[38]，如图8所示，该设计思想尚未在成像光学系统设计中得到应用。
-
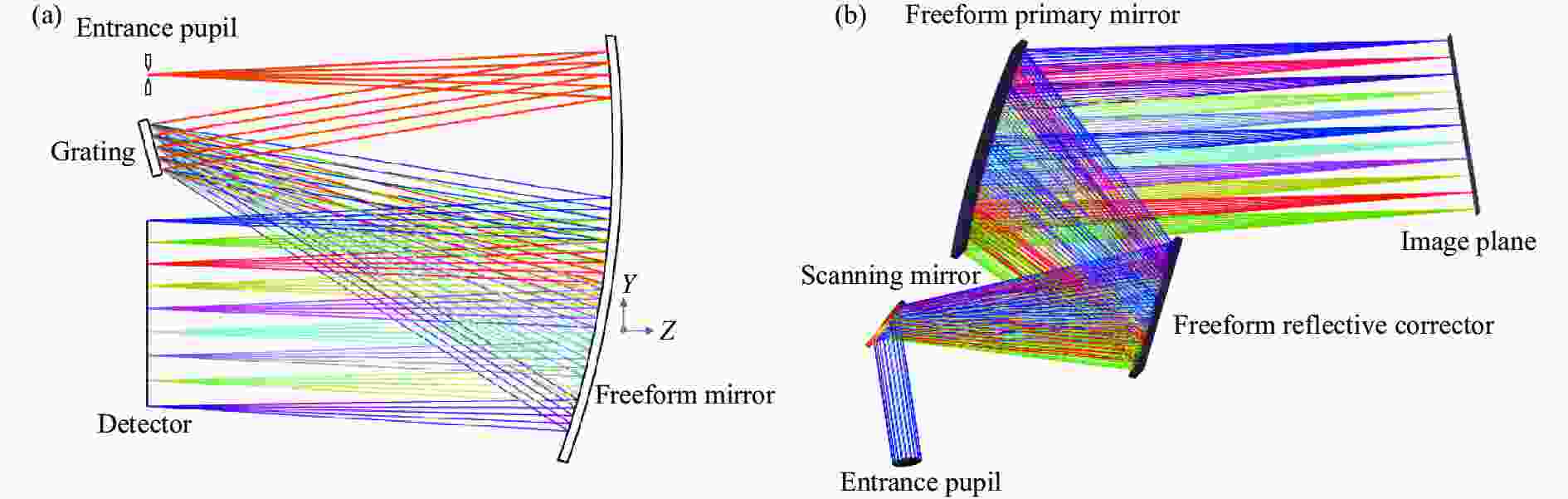
2019年，南京理工大学高志山团队利用离轴抛物面反射镜对无限远物体完善成像且不存在孔径遮拦的优势，结合分段拼接融合的面型构造思想[39]，将全视场分割为多个单视场单元，构建多个小孔径离轴抛物面子镜分别对单视场完善成像，再由各离轴抛物面子镜单元扩展融合形成自由曲面面型，完成光学系统初始结构的构建，并在此基础上优化设计得到带宽400 nm，光谱分辨率0.1 nm的Czerny-Turner型成像光谱仪，如图9 (a)所示[40]。2020年，该团队在此设计思想基础上，进一步提出多面对融合型自由曲面两反成像系统的设计方法，利用抛物面子镜与平面子镜相配合同时实现对光束远心度的控制和畸变的校正，达到无畸变远心成像的效果，完成f-θ离轴两反远心扫描系统的设计，如图9 (b)所示[41]。
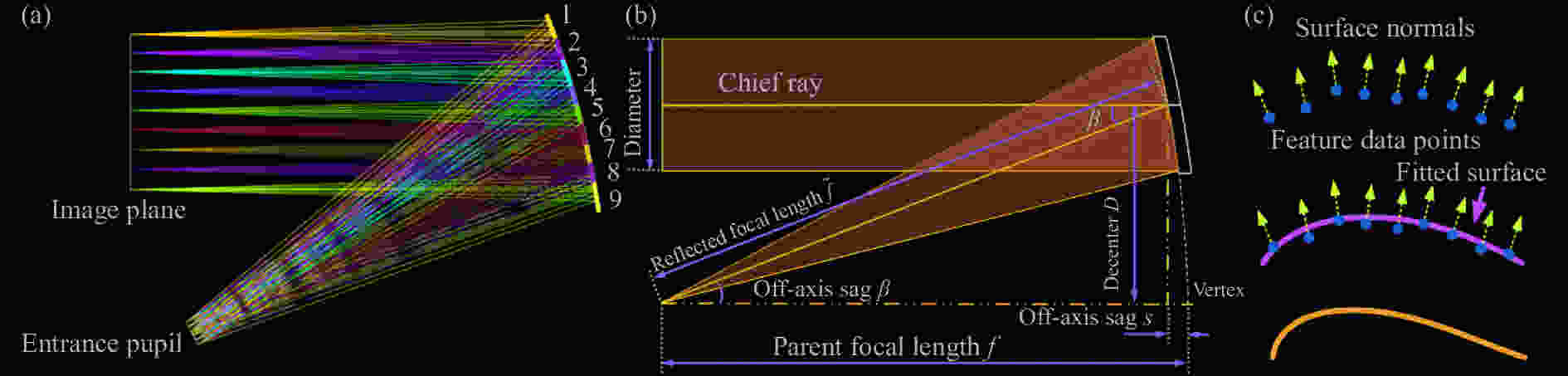
应用抛物面扩展融合的设计思想构造初始结构分为三个步骤[42]，如图10 (a)所示。(1) 根据成像系统设计指标对视场或孔径进行划分，将系统解构为若干个小视场/小孔径子系统的组合，各子系统光线分别对应一个小的离轴抛物面子镜，在后续子镜求解过程中，认为各子系统之间相互独立，设计过程互不干扰；(2) 针对各子系统分别求解离轴抛物面子镜面型参数，如图10 (b)所示，以其中一个子镜为例，其反射焦距$ \overline{f} $和离轴角β为一对特征参量，依据特征参量可由公式(9)、(10)求解离轴反射镜的其他几何参数值，包括离轴量为D，主光线与子镜交点位置矢高为s，子镜母抛物面焦距为f，曲率半径为R。
$$ s = \frac{{{D^2}}}{{2R}} = \frac{{{D^2}}}{{4f}} $$ (9) $$ \overline f = f + s $$ (10) $$ \mathrm{tan}\;\beta =\frac{D}{f-s}=\frac{2RD}{{R}^{2}-{D}^{2}} $$ (11) $$ D = \frac{{R\;(1 - \cos \;\beta )}}{{\sin\; \beta }} $$ (12) 在完成了所有子系统的设计后，对子镜面型进行拼接融合，在第二步求解得到的子镜结构参数基础上构造一个完整的自由曲面。拼接融合过程中主要解决的问题是各子镜重叠区域的重新构建以及由于子镜拼接处矢高不连续、斜率不相等导致的面型不平滑。由于表面法线方向直接决定出射光线的方向，如图10 (c)所示，采用兼顾采样数据点的坐标和法向量拟合法以获得高精度的自由曲面面型。自此完成自由曲面成像光学系统初始结构的设计，在后续的设计优化中，只需要在初始结构的基础上，对系统布局和面型参数进行微调即可完成系统设计。
利用抛物面扩展融合的初始结构设计方法充分发挥了离轴抛物面无像差、无中心遮拦的优势，构建多个可完善成像的曲面子区域，实现多个对应视场点的理想成像，而后将这些子区域进行拼接融合，得到充分逼近系统像差要求的初始结构。这种小视场/小孔径子镜扩展融合生成复杂面型的设计思想同样适用于同轴光学系统初始结构的构造，2020年，高志山团队将这一面型构造思想与双同心球结构相结合，实现了全视场90°、系统总长2.81 mm的医用内窥物镜设计[43-44]。
-
自由曲面在成像光学系统中的应用是光学设计领域革命性的发展，但由于针对自由曲面光学系统的像差理论尚不成熟，因此对于普适化初始结构设计方法的研究仍在探索中。另一方面，自由曲面面型的表征方式具有多样性，目前的主流方案仍是采用Zernike或者XY多项式作为设计变量，探索其他具有更多自由度、更强表征能力的表征函数在光学设计中的应用十分必要。南京理工大学研究团队针对上述问题开展了相关研究工作，先后提出基于矩阵变换的数值化正交梯度多项式表征光学自由曲面、结合面型和视场优化策略的自由曲面设计方法以及分段拼接融合型光学设计方法。
文中聚焦于自由曲面成像光学系统设计中的初始结构构造方法，整理并分析了自由曲面成像光学系统发展过程中出现的各类初始结构设计方法，包括同轴系统离轴化法、直接设计法、视场孔径扩展法和分段拼接融合设计法。如何将像差理论与初始结构的构建相结合，充分发挥自由曲面设计自由度高、面型表征能力强、像差校正能力突出的优势仍是自由曲面成像光学系统设计亟待解决的问题。
Review of design methodology for starting-point of freeform surface imaging optical system
-
摘要: 自由曲面设计自由度多、面型表征能力强等优势使成像光学系统突破了传统面型表征和系统结构的限制，在进一步提高成像质量的同时可以实现大视场、大孔径、小型化、轻量化等设计目标。良好的初始结构可以充分发挥自由曲面对像差的校正能力，提高系统设计效率。与共轴光学系统相比，自由曲面成像光学系统设计存在可参考样例少、像差理论尚不完善等问题，其初始结构的构造与求解仍然是先进光学设计领域的前沿热点问题之一。结合课题组多年的研究心得，探讨了现有的自由曲面成像光学系统初始结构设计方法，依据自由曲面构造原理将其分为同轴系统离轴化法、直接设计法、视场孔径扩展法和分段拼接融合设计方法，并分别介绍其设计原理和思路。最后对自由曲面成像光学系统初始结构设计中亟待解决的问题进行了分析总结。Abstract: Freeform surface provides more degrees of freedom for optical system and stronger capability of aberration correction to break the limitation of traditional surface characterization and system structure, which helps engineer to achieve large field of view, large aperture, miniaturization, and lightweight optical system design while improving the imaging quality. A favorable starting-point of freeform surface imaging optical system design can release the potential of freeform surface to correct aberration and improve the efficiency of system design. Comparing to coaxial optical systems, few examples can be referred to for freeform surface imaging optical system and theory for freeform is not perfect yet. Therefore, how to construct and solve a favorable starting-point of freeform surface imaging optical system is one of the frontier issues in the field of optical design. Based on the research experience of author team for many years, this review summarizes the current design methods of freeform surface imaging optical system design, and divides them into disturbing coaxial system method, directly solving method, and expending field or aperture method and stitching and fusion method, according to the construction principle of freeform surface. Finally, the problems to be solved in the design starting-point for freeform surface imaging optical system are analyzed and summarized.
-
Key words:
- optical design /
- freeform surface /
- imaging system /
- starting-point
-
图 1 离轴化的不同结构型式。(a) 4型结构的离轴两反系统； (b) Z型结构的离轴两反系统； (c)~(j)离轴三反系统的八种结构型式
Figure 1. Different off-axis structures. (a) 4-type structure off-axis two-reflective system; (b) Z-type structure two-reflective system; (c)-(j) Eight structural types of off-axis three-reflective system
图 2 偏微分方程法原理示意图
Figure 2. Schematic of the principle of partial differential equation method
图 5 视场扩展示意图。 (a) X方向视场扩展； (b) Y方向视场扩展
Figure 5. Schematic of expending FOV. (a) Expanding the FOV in the X; (b) Expanding the FOV in the Y
图 6 基于自由曲面的交替优化方法流程图
Figure 6. Flow chart of alternate optimization method based on freeform surface
-
[1] Li X Y, Ni D W, Yang M Y, et al. Design of large field of view space camera optical system based on freeform surfaces [J]. Acta Optica Sinica, 2018, 47(9): 0922003. (in Chinese) [2] Ye J F, Yu J, Song Z Z, et al. Design of a compact off-axis two-mirror freeform infrared imager with a wide field of view [J]. Journal of Modern Optics, 2018, 66(3): 1-8. [3] Ye J F, Xu K D, Yang M Z, et al. Design of off-axis head-mounted display optical system based on two reflective optical free-form surfaces [J]. Acta Optica Sinica, 2018, 38(7): 0722003. (in Chinese) doi: 10.3788/AOS201838.0722003 [4] Su P C, Chen Y, Zhang J M, et al. Design of bionic compound eye system based on hexagonal closely spliced structure [J]. Infrared and Laser Engineering, 2021, 50(4): 20200338. (in Chinese) doi: 10.3788/IRLA20200338 [5] Jiang Y, Quan X Q, Du J, et al. Design of deep-sea optical imaging system with wide field of view and ultra-high resolution [J]. Optics and Precision Engineering, 2019, 27(11): 2289-2295. (in Chinese) doi: 10.3788/OPE.20192711.2289 [6] Zhang Jialun, Zheng Yuquan, Lin Chao, et al. Design of a freeform curved prism imaging spectrometer based on an anastigmatism [J]. Chinese Optics, 2020, 13(4): 842-851. (in Chinese) doi: 10.37188/CO.2019-0049 [7] Mao S S, Li Y Q, Liu K, et al. Optical design of high numerical aperture extreme ultraviolet lithography objective with freeform surfaces [J]. Infrared and Laser Engineering, 2019, 48(8): 0814002. (in Chinese) doi: 10.3788/IRLA201948.0814002 [8] Yang T, Duan Y Z, Cheng D W, et al. Freeform imaging optical system design: Theories, development, and applications [J]. Acta Optica Sinica, 2021, 41(1): 0108001. (in Chinese) doi: 10.3788/AOS202141.0108001 [9] Xu L D, Fang A L, Yu J H, et al. Ultrasonic-vibration assisted grinding of a zerodour freeform optical mirror [J]. Optics and Precision Engineering, 2019, 27(12): 2564-2570. (in Chinese) doi: 10.3788/OPE.20192712.2564 [10] Liang Z J, Yang Y Y, Zhao H Y, et al. Advances in research and application of optical aspheric surface metrology[J/OL]. [2021-10-19]. http://www.chineseoptics.net.cn/cn/article/doi/10.37188/CO.2021-0143. [11] Thompson K P, Rolland J P. Freeform optical surfaces: A revolution in imaging optical design [J]. Optics & Photonics News, 2012, 23(6): 30-35. [12] Ye J F, Chen L, Li X H, et al. Review of optical freeform surface representation technique and its application [J]. Optical Engineering, 2017, 56(11): 110901. [13] Bauer A, Schiesser E M, Rolland J P. Starting geometry creation and design method for freeform optics [J]. Nature Communications, 2018, 9(1): 1756. doi: 10.1038/s41467-018-04186-9 [14] Kyle Fuerschbach, Jannick P Rolland, Kevin P Thompson. A new family of optical systems employing φ-polynomial surfaces [J]. Optics Express, 2011, 19(22): 21919-21928. doi: 10.1364/OE.19.021919 [15] Trumper I, Anderson A Q, Howard J M, et al. Design form classification of two-mirror unobstructed freeform telescopes [J]. Optical Engineering, 2020, 59(2): 025105. [16] Wassermann G D, Wolf E. On the theory of aplanatic aspheric systems [J]. Proceedings of the Physical Society, Section B, 1949, 62(1): 2-8. doi: 10.1088/0370-1301/62/1/302 [17] Vaskas E M. Note on the Wasserman-Wolf method for designing aspheric surfaces [J]. Journal of the Optical Society of America, 1957, 47(7): 669-670. doi: 10.1364/JOSA.47.000669 [18] Knapp D J. Conformal optical design [D]. Arizona: University of Arizona, 2002. [19] Hicks R A. Direct methods for freeform surface design[C]// Proceedings of SPIE, Conference on Novel Optical Systems Design and Optimization X, 2007, 6668: 666802. [20] Cheng D W, Wang Y T, Hua H. Free form optical system design with differential equations[C]//Proceedings of SPIE, 2010, 7849: 78490Q. [21] Miñano J C, Benítez P, González J C. RX: A nonimaging concentrator [J]. Applied Optics, 1995, 34(13): 2226-2235. doi: 10.1364/AO.34.002226 [22] Miñano J C, Benítez P, Wang L, et al. An application of the SMS method for imaging designs. [J]. Optics Express, 2009, 17(26): 24036-24044. doi: 10.1364/OE.17.024036 [23] Duerr F, Benítez P, Miñano J C, et al. Analytic free-form lens design in 3D: Coupling three ray sets using two lens surfaces [J]. Optics Express, 2012, 20(10): 10839-10846. doi: 10.1364/OE.20.010839 [24] Nie Y, Thienpont H, Duerr F. Multi-fields direct design approach in 3D: Calculating a two-surface freeform lens with an entrance pupil for line imaging systems [J]. Optics Express, 2015, 23(26): 34042-34054. doi: 10.1364/OE.23.034042 [25] Nie Y, Mohedano R, P Benítez, et al. Multifield direct design method for ultrashort throw ratio projection optics with two tailored mirrors [J]. Applied Optics, 2016, 55(14): 3794-3800. doi: 10.1364/AO.55.003794 [26] Zhu J, Yang T, Jin G F. Design method of surface contour for a freeform lens with wide linear field-of-view [J]. Optics Express, 2013, 21(22): 26080-26092. doi: 10.1364/OE.21.026080 [27] Yang T, Zhu J, Jin G F. Design of freeform imaging systems with linear field-of-view using a construction and iteration process [J]. Optics Express, 2014, 22(3): 3362-3374. doi: 10.1364/OE.22.003362 [28] Yang T, Zhu J, Hou W, et al. Design method of freeform off-axis reflective imaging systems with a direct construction process [J]. Optics Express, 2014, 22(8): 9193-9205. doi: 10.1364/OE.22.009193 [29] Yang T, Zhu J, Wu X F, et al. Direct design of freeform surfaces and freeform imaging systems with a point-by-point three-dimensional construction-iteration method [J]. Optics Express, 2015, 23(8): 10233-10246. doi: 10.1364/OE.23.010233 [30] Zhu J, Wu X, Yang T, et al. Generating optical freeform surfaces considering both coordinates and normals of discrete data points [J]. Journal of the Optical Society of America A Optics Image Science & Vision, 2014, 31(11): 2401-2408. [31] Yang T, Zhu J, Jin G. Starting configuration design method of freeform imaging and afocal systems with a real exit pupil [J]. Apply Optics, 2016, 55(2): 345-353. doi: 10.1364/AO.55.000345 [32] Yang T, Jin G F, Zhu J. Automated design of freeform imaging systems [J]. Light: Science & Applications, 2017, 6(10): e17081. [33] Yao Y X. Research on optimization strategy and design method of off-axis reflection free-form surface optical system[D]. Nanjing: Nanjing University of Science and Technology, 2019. (in Chinese) [34] Yao Y X, Yuan Q, Chen L, et al. Freeform surface design method combined with surface and field-of-view optimization [J]. Infrared and Laser Engineering, 2018, 47(10): 1018001. (in Chinese) doi: 10.3788/IRLA201847.1018001 [35] Meng Q Y, Wang H Y, Liang W J, et al. Design of off-axis three-mirror systems with ultrawide field of view based on an expansion process of surface freeform and field of view [J]. Applied Optics, 2019, 58(3): 609-615. doi: 10.1364/AO.58.000609 [36] Korsch D. Reflective Optics[M]. US: Academic Press, 1991. [37] Yang J, Liu W, Lv W, et al. Method of achieving a wide field-of-view head-mounted display with small distortion [J]. Optics Letters, 2013, 38(12): 2035-2037. doi: 10.1364/OL.38.002035 [38] Fournier F R, Cassarly W J, Rolland J P. Designing freeform reflectors for extended sources[C]//Proceedings of SPIE, 2009, 7423: 742302. [39] Cheng D W, Chen X J, Xu C, et al. Optical description and design method with annularly stitched aspheric surface [J]. Applied Optics, 2015, 54(34): 10154-10162. doi: 10.1364/AO.54.010154 [40] Chen L, Gao Z S, Ye J F, et al. Construction method through multiple off-axis parabolic surfaces expansion and mixing to design an easy-aligned freeform spectrometer [J]. Optics Express, 2019, 27(18): 25994-26013. doi: 10.1364/OE.27.025994 [41] Chen L, Gao Z S, Xu N Y, et al. Construction of freeform mirrors for an off-axis telecentric scanning system through multiple surfaces expansion and mixing [J]. Results in Physics, 2020, 19: 103354. doi: 10.1016/j.rinp.2020.103354 [42] Chen L. Study of optical design method for imaging system based on stitching and fusion of segmented surfaces[D]. Nanjing: Nanjing University of Science and Technology, 2021. (in Chinese) [43] Cao X. Research on design method of optical system based on field of view segmentation[D]. Nanjing: Nanjing University of Science and Technology, 2021. (in Chinese) [44] Cao X, Gao Z S, Xu N Y, et al. Design of electronic endoscope objective lens optical system based on annularly stitched surface [J]. Chinese Journal of Lasers, 2021, 48(21): 2107003. (in Chinese) doi: 10.3788/CJL202148.2107003 -
点击查看大图
图(10)
计量
- 文章访问数: 878
- HTML全文浏览量: 186
- PDF下载量: 180
- 被引次数: 0
