微流控芯片（Microfluidic chip）作为微流控系统的主要实验平台，由于其具有体积轻巧、结构功能多样化、反应速度快等优点，在物理、生物分析和疾病诊断等领域中有着广阔的应用前景^[1]。微通道作为微流控芯片的基本结构，芯片加工过程中任何不当操作都可能会造成通道表面出现划痕、微小断裂、破边等疵病缺陷，而通道的质量又直接影响到微流控系统中样品的分离、进样、反应和测量，因此对微流控芯片通道的三维形貌检测具有重要意义。

数字全息显微术（Digital holographic microscopy, DHM）是数字全息术与显微术相结合的产物，其不仅具有三维成像能力，还具有有非破坏性、高分辨率、实时性等优点，目前已被广泛应用于形变测量、光学元件表面缺陷检测等领域^[2-4]。近年来，像面数字全息显微术（Image plane digital holographic microscopy, IPDHM）由于其具有许多优于其他类型数字全息术的优点^[5]，因此也被广泛地应用于微观结构测量领域^[6]。由于微流控芯片的通道结构尺寸通常在微米、亚微米级别，通道材料为硬度较低的有机聚合物，因此要求检测方法具有高分辨率、无损等特点。传统的成像方法有探针式轮廓仪，但该方法对硬度较低的样品容易造成损坏，并且不能实时观测。电子显微镜^[7]可以拥有纳米级的检测精度，但这种方法只能获得二维信息。此外，共聚焦激光扫描显微镜^[8-9]、扫描探针显微镜^[10]可用于被测样品表面三维形貌测量，但是这些方法需要复杂的扫描结构，并且工作效率较低、成本较高，测量范围也受到限制。近年来，数字全息显微术在微流控芯片定量检测方面已得到初步应用^[11-12]，例如北京工业大学王喆等人利用双波长数字全息实现了微流控芯片内流动细胞的定位、计数和未知浓度溶液的折射率测量^[11]，麻省理工学院Sung Yongjin等人通过离轴数字全息技术实现了微流控芯片通道中连续流动细胞的折射率、体积和密度测量^[12]。但目前的研究主要集中于对微流控芯片通道内液体、细微颗粒物、生物细胞等样品的相关特性研究，对微流控芯片通道及表面缺陷的研究还比较少。

因此，为实现对微流控芯片通道及缺陷的三维形貌测量，文中首先对像面数字全息显微技术的原理和相位畸变的矫正进行探讨，设计和构建了一套反射式离轴像面数字全息显微实验系统。然后给出台阶标准样板的成像实验结果，并对两步相位相减法和曲面拟合法的相位畸变矫正效果进行对比研究。最后基于反射式离轴像面数字全息显微实验系统，对微流控芯片的通道和表面缺陷进行三维形貌检测。

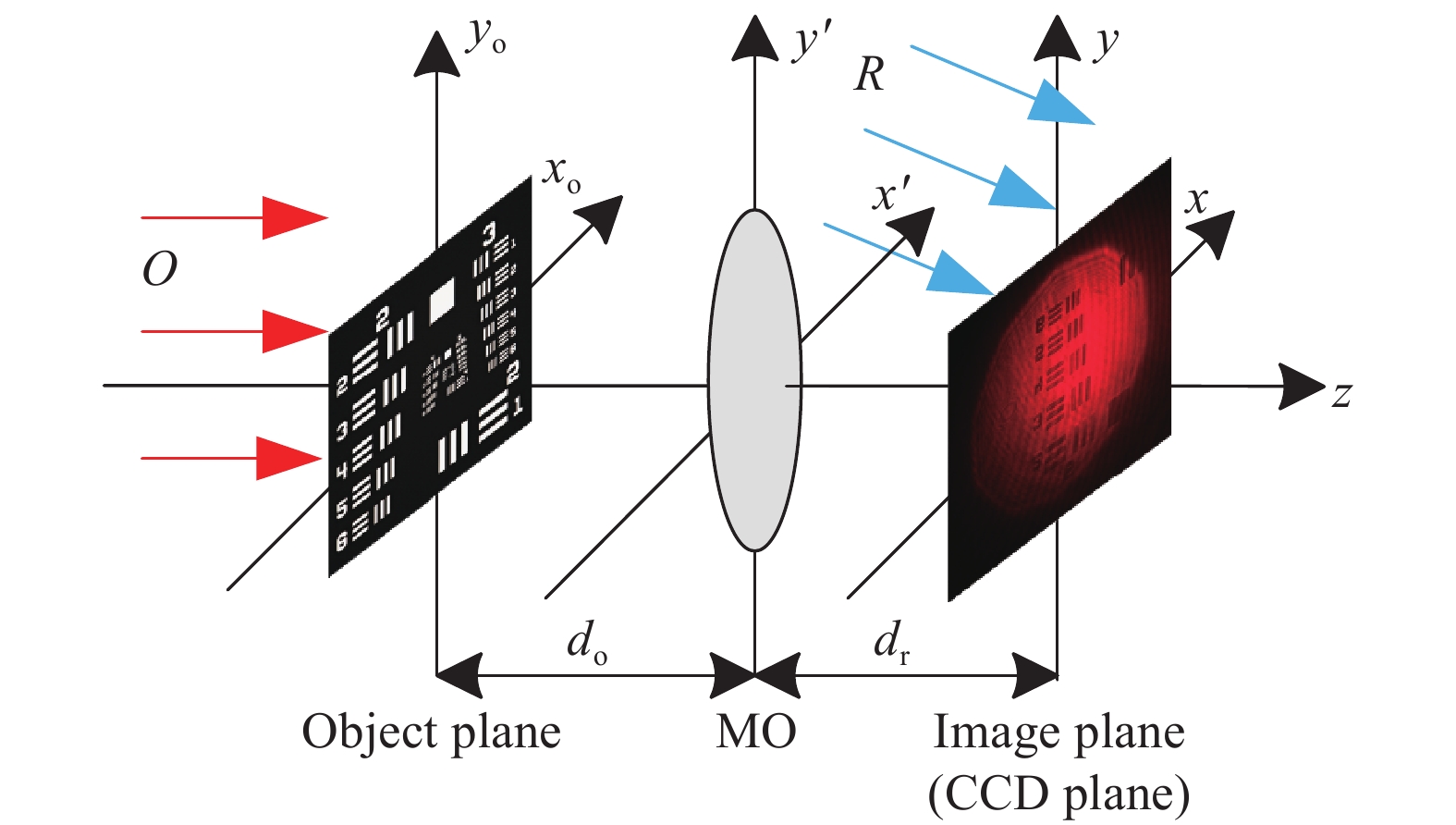
数字全息显微术是在数字全息术的基础上加入显微放大形成的，CCD光敏面记录的是经过显微物镜放大后的物光和平面参考光的干涉条纹。为了便于分析，建立如图1所示的坐标系统，其中$ {x_{\text{o}}} - {y_{\text{o}}} $表示物平面，$ x' - y' $表示显微物镜所在平面，CCD记录面和显微物镜聚焦成像面为同一个平面，用$ x - y $表示。

图  1  系统坐标示意图

Figure 1.  Schematic diagram of system coordinates

在理想成像条件下，假设物光波光场分布为$ {O_{\text{o}}}({x_{\text{o}}},{y_{\text{o}}}) $，则在CCD记录面的物光波分布为：

式中：k为波数，$ k{\text{ = 2\pi }}/\lambda $ ；$ \lambda $为测量光源的波长；$ {d_{\text{o}}} $和$ {d_{\text{r}}} $分别为物距和像距；$ M = - {d_{\text{r}}}/{d_{\text{o}}} $为系统的放大倍数；f为显微物镜的焦距。

假设参考光波为$ R(x,y) $，则CCD光敏面上记录的总光强分布为：

式中：上标$ * $表示复共轭运算。总光强共包含四项，前两项为零级项，第三项和第四项分别为原始项和共轭项。

对于像面数字全息显微来说，由于CCD记录的是物体放大后的聚焦像，全息图记录距离为零，再现距离也为零。因此，数值再现过程无需进行衍射传播计算。此外，为了消除零级项和共轭项的干扰，采用频域滤波的方法将频谱中原始像的频谱提取出来，再对其进行一次逆傅里叶变换即可得到所需要的再现物光波前，其可表示为：

式中：下角标$ filter $表示滤除频谱中的零级项和共轭项的频谱；$ \mathcal{F} $和$ {\mathcal{F}}^{-1} $分别表示傅里叶变换和逆傅里叶变换运算。由公式（3）计算得到的是一个复数，对其进行取模和求幅角便可得到再现像的光强和相位分布。

对于数字全息显微光路中离轴记录方式引起的一次相位畸变$ {\varphi _{\text{t}}}(x,y) $（呈斜面分布）和显微物镜引入的二次相位畸变$ {\varphi _{\text{s}}}(x,y) $（呈球面分布），以及光学系统、实验环境等引起的其他相位畸变$ {\varphi _{\text{e}}}(x,y) $，会使物体自身相位难以恢复，严重影响被测物的三维形貌测量。为了获得物体正确的相位像，在数值再现计算中需要对畸变相位进行相位矫正。参考文献[13]详细介绍了目前数字全息显微技术中矫正相位畸变的方法，主要分为数值补偿法和物理补偿法两类。

数值补偿法是在计算机中，通过数值再现进行畸变矫正，主要包括相位掩模法、横向剪切重建法和曲面拟合法。相位掩模法需要对掩模参数反复进行手工调整和运算，计算过程较为耗时而且使用上需要丰富的实验经验^[14]。横向剪切重建法虽然可以在不用相位解包裹的情况下获得再现物光场的准确相位分布，但它对噪声比较敏感，容易产生较大的重建误差^[15]。相较于前面两种方法，曲面拟合法只需要单张全息图即可矫正相位畸变，并且无需获取物距、像距等位置信息，算法简洁快速，因此文中主要讨论数值补偿法中的曲面拟合法。

曲面拟合法矫正相位畸变的原理是利用一般多项式或者Zernike高阶多项式^{[13, 16-17]}对再现相位进行曲面拟合，然后将再现相位与拟合的畸变相位相减，获得不含畸变的物体真实相位分布，具体过程如下所述。

假设物体真实的相位分布为$ {\varphi _{\text{o}}}(x,y) $，解包裹后的再现总相位$ {\varphi _{\text{a}}}_{{\text{ll}}}(x,y) $既包含物体相位又包含所有的畸变相位，其可表示为：

当物体的横向尺寸较小时，也就是被测物在干涉场中的视场远小于感兴趣的测量区域视场时，物体相位相当于总畸变相位上的一个小的扰动，曲面拟合过程中物体相位将被当作异常数据点而忽略。因此拟合得到的相位$ {\varphi _{\text{f}}}(x,y) $就是总的畸变相位$ {\varphi _{\text{t}}}(x,y) + {\varphi _{\text{s}}}(x,y) + {\varphi _{\text{e}}}(x,y) $，此时物体的真实相位可用$ {\varphi _{{\text{all}}}}(x,y) - {\varphi _{\text{f}}}(x,y) $得到。但当被测物在干涉场中的视场相对于感兴趣的测量区域视场较大时，曲面拟合的过程中物体的相位数据不会被忽略，此时$ {\varphi _{\text{f}}}(x,y) \ne {\varphi _{\text{t}}}(x,y) + {\varphi _{\text{s}}}(x,y) + {\varphi _{\text{e}}}(x,y) $，用$ {\varphi _{{\text{all}}}}(x,y) - {\varphi _{\text{f}}}(x,y) $计算物体的真实相位将会产生拟合误差。

物理补偿法主要包括参考光路补偿法、远心结构光路法和两步相位相减法。参考光路补偿法通过在物、参光路中各放置一个显微物镜来消除二次相位畸变，该方法需要精确调节参考光路中显微物镜的位置，时间成本和经济成本都比较高。远心结构光路法通过在物光路显微物镜后面放置一个准直透镜来补偿相位畸变，在光学布置上需要精确调整显微物镜孔径光阑和准直透镜之间的距离，容易产生残余像差。因此，文中主要讨论物理补偿法中的两步相位相减法。两步相位相减法^[18]的原理如下：在同一个光路系统和记录条件下，首先采集物体周围空白区域的参考背景全息图，然后通过数值再现和相位解包裹算法获得背景区域的解包裹相位，其可表示为：

式中：$ {\varphi _{\text{r}}}(x,y) $表示参考背景区域的真实相位。然后采集物体全息图，经过数值再现和相位解包裹后的物体解包裹相位可表示为：

由于两幅全息图是在同一记录系统和同样的记录条件下采集的，因此背景区域和物体区域的解包裹相位中所包含的畸变相位是相同的，将两个解包裹相位进行相减即可消除相位畸变，从而得到物体真实的相位分布$ {\varphi _{\text{p}}}(x,y) $

参考背景区域为平坦区域，在理想情况下，其相位$ {\varphi _{\text{r}}}(x,y) = 0 $，因此$ {\varphi _{\text{p}}}(x,y) = {\varphi _{\text{o}}}(x,y) $。由上述分析可以看出，两步相位相减法不仅能够消除一次畸变和二次畸变，而且还能消除成像系统的其他畸变。即使被测物在干涉场中的视场相对于感兴趣的测量区域视场较大时，也就是物体的相位分布相对于总的畸变相位不可忽略时，两步相位相减法依然适用。

基于上述理论分析，文中采用如图2所示的反射式离轴像面数字全息显微实验系统。He-Ne激光器（λ=632.8 nm）发出的光经过偏振片、准直扩束系统BE后由分光镜BS1分成物光和参考光两路光束，物光经过显微物镜MO（10倍）照射到物体表面反射回来，并由分光镜BS2反射与参考光发生干涉，干涉条纹被CCD（像元尺寸为2.775 μm×2.775 μm，像素数为 2608×1 950 pixel）记录下来。通过标准分辨率靶USAF1951对实验系统进行标定后，系统实际放大倍数为12.7倍。

图  2  反射式离轴像面数字全息显微实验系统示意图

Figure 2.  Schematic of the experimental system of reflective off-axis IPDHM

对于横向尺寸较大的低空间频率物体的相位畸变矫正，参考文献[19]通过对比分析两步相减法和Zernike多项式曲面拟合法的仿真和实验结果，指出Zernike多项式补偿法的使用需要保证物体的光学高度或者横向尺寸在一个较小的范围内变化。但其选用的仿真对象是近似半球形的生物细胞，与文中选用的台阶被测样件轮廓外形相差较大，并且缺少对其他数学模型的讨论。因此文中首先选择两种常用于曲面拟合法矫正相位畸变的二次多项式^[16-17]，并根据参考文献[13]选择Zernike前9项高阶多项式分别对高度为65 nm的台阶标准样板的再现相位矫正畸变。将矫正畸变后的台阶相位换算成台阶高度，矫正结果如图3所示。

图  3  不同多项式的曲面拟合法矫正结果。（a） 6项二次多项式；（b） 9项二次多项式；（c） Zernike高阶多项式

Figure 3.  Correction results of surface fitting method for different polynomials. (a) 6-term quadratic polynomial; (b) 9-term quadratic polynomial; (c) Zernike higher order polynomial

然后，再通过两步相位相减法获得台阶标准样板的三维形貌，实验结果如图4所示。实验中将台阶放于持物架上，在保持光路结构、物距等参数不变的情况下，用CCD分别拍摄背景区域和台阶的全息图，如图4（a）、（b）所示。由于系统的全息图记录平面与台阶的像平面重合，因此数值再现过程只需对滤波后的频谱进行一次逆傅里叶变换，得到再现振幅如图4（c）、（d）所示。采用基于离散余弦变换最小二乘解包裹算法对包裹相位进行解包裹后得到背景区域和台阶的解包裹相位，如图4（e）、（f）所示。从解包裹相位图上可以看出，背景区域的相位和台阶的相位完全淹没在畸变相位中。为了矫正畸变相位，用背景区域的解包裹相位减去台阶的解包裹相位得到不含畸变的台阶的真实相位，再将台阶相位换算成台阶高度，得到台阶的高度图和三维形貌如图4（g）和图4（h）所示。从图4（g）中可以看出台阶的横向尺寸较大，其占据的区域超过了感兴趣的测量视场的1/2。

图  4  台阶标准样板的两步相位相减法实验结果。（a）背景全息图；（b）台阶全息图；（c）背景区域再现振幅；（d）台阶再现振幅；（e）背景区域解包裹相位；（f）台阶解包裹相位；（g）台阶高度图；（h）台阶三维形貌

Figure 4.  Experimental results of two-step phase subtraction method for micro-step. (a) Backgroud area hologram; (b) Micro-step hologram; (c) Reconstructed amplitude of background area; (d) Reconstructed amplitude of micro-step; (e) Unwrapped phase of backgroud area; (f) Unwrapped phase of micro-step; (g) Height distribution of micro-step; (h) 3D diagram of micro-step

为了便于分析，以相对误差（RE）为客观评价方法来衡量两步相位相减法和曲面拟合法在相位畸变矫正上的有效性。以矫正畸变后的台阶平均高度为测量值，相对误差用H_RE表示，比较结果如表1所示。从表中可以看出，用两步相位相减法矫正相位畸变后的台阶平均高度与参考值65 nm最为接近，而通过Zernike前9项高阶多项式进行曲面拟合矫正相位畸变后得到的台阶高度与参考值偏离程度最大。

此外，对图3和图4中矫正畸变后的台阶高度图分别选取y=200 pixel处的截面曲线与日本东京精密粗糙度测量仪SURFCOM 1910 DX3测得的台阶高度曲线图进行比较，结果如图5所示。从截面曲线对比图中可以看出，粗糙度仪测得的台阶宽度为55.8 μm，横向尺寸较大。用两步相位相减法矫正相位畸变后的台阶高度、轮廓与粗糙度仪所测结果一致性较好，台阶高度为(65±5) nm。而通过6项二次多项式、9项二次多项式以及Zernike高阶多项式进行曲面拟合矫正相位畸变后的台阶相位依然存在畸变，并且该畸变使得台阶在有阶跃高度的区域向下凹，台阶两侧背景区域向上倾斜，台阶的高度、轮廓与粗糙度仪所测结果都存在较大误差。通过对台阶标准样板实验结果的处理及对比分析可知，两步相位相减法更适合于横向尺寸较大的低空间频率物体的相位畸变矫正。

图  5  两步相位相减法和曲面拟合法矫正实验结果比较

Figure 5.  Comparison of experimental results of two-step phase subtraction method and surface fitting method

实验中检测所用的微流控芯片，通过精密电铸工艺加工出高精度金属模具，然后利用一体式精密注塑技术得到与模具凹凸性相反的微流控芯片，芯片通道宽度为80 μm。由于通道宽度在数十微米级别，横向尺寸较大，结合2.1节的台阶标准样板的实验分析比较结果，因此采用两步相位相减法矫正相位畸变。通过像面数字全息显微实验装置记录微流控芯片通道的全息图，如图6（b）所示，图6（d）是通道的部分再现振幅。然后拍摄另一张无通道的背景区域全息图，其全息图和再现振幅分别如图6（a）、（c）所示。通过相位解包裹算法后分别获得解包裹相位，如图6（e）、（f）所示。再将两个解包裹相位进行相减矫正相位畸变，图6（g）和图6（h）给出了通道的深度图和三维形貌图，从图中可以看出，经过两步相减法矫正畸变后，通道两侧的平坦背景区域没有出现倾斜现象，畸变得到了很好的矫正。经实验系统实际放大倍数换算后，通道的宽度为78.7 μm，与设计值相比，测量误差为1.7%。

图  6  微流控芯片通道的实验结果。（a）背景区域全息图；（b）通道全息图；（c）背景区域再现振幅；（d）通道再现振幅；（e）背景区域解包裹相位；（f）通道解包裹相位；（g）通道深度图；（h）通道三维形貌

Figure 6.  Experimental results of the microfluidic chip channel. (a) Background area hologram; (b) Channel hologram; (c) Reproducted amplitude of background area; (d) Reproducted amplitude of channel; (e) Unwrapped phase of background area; (f) Unwrapped phase of channel; (g) Depth of channel; (h) 3D diagram of channel

此外，对微流控芯片加工过程中随机出现的断裂型和缺损型表面缺陷进行检测，其像面数字全息显微实验结果如图7和图8所示。从图7（a）的再现振幅中可以看出在微流控芯片通道上出现一处斜穿通道表面的断裂缺陷，其再现振幅放大图如图7（b）所示，选取断裂区域进行再现获得缺陷的深度图和三维形貌分别如图7（c）、（e）所示。经过实际放大倍数换算后，图7（c）中虚线处的缺陷宽度为14.1 μm。为了方便测量缺陷的深度信息，选取图7（c）中实线处的深度值进行作图，得到缺陷的深度截面曲线如图7（d）所示。从截面曲线上可以看出，该断裂型缺陷的深度为431.7 nm。

图  7  断裂型表面缺陷的实验结果。（a）通道及缺陷再现振幅；（b）缺陷再现振幅放大图；（c）缺陷深度图；（d）图（c）中横线处深度截面曲线；（e）缺陷三维形貌

Figure 7.  Experimental results of fractured surface defect. (a) Reproducted amplitude of channel and defect; (b) Magnified view of defect’s reproducted amplitude; (c) Depth of defect; (d) Depth distribution of the horizontal line in (c); (e) 3D diagram of defect

图  8  缺损型表面缺陷的实验结果。（a）通道及缺陷再现振幅；（b）缺陷再现振幅放大图；（c）通道及缺陷深度图；（d）图（c）中横线处深度截面曲线；（d）缺陷三维形貌

Figure 8.  Experimental results of defective surface defect. (a) Reproducted amplitude of channel and defect; (b) Magnified view of defect’s reproducted amplitude; (c) Depth of channel and defect ; (d) Depth distribution of the horizontal line in (c); (d) 3D diagram of defect

除断裂型缺陷外，缺损型表面缺陷也是加工中常出现的一种缺陷。文中对通道表面随机出现的一处缺损型缺陷进行检测，缺陷的再现振幅如图8（b）所示。图8（c）是利用两步相位相减法矫正相位畸变后通道和缺陷整体深度分布图，为方便直观感受通道表面的损伤程度，图8（e）给出了缺陷的三维形貌。为了获取缺陷的宽度和深度参数，选取图8（c）实线处的深度分布信息进行作图，得到深度截面曲线如图8（d）所示。从缺陷的深度截面曲线中可以看出，缺陷的宽度为33.6 μm，深度为295.1 nm。

针对微流控芯片通道和缺陷检测，文中在理论分析的基础上，构建反射式离轴像面数字全息显微实验装置。通过台阶标准样板实验，分析和比较了两步相位相减法和曲面拟合法对横向尺寸在视场占比较大的低空间频率物体的相位畸变矫正效果。同时利用日本东京精密粗糙度仪对台阶进行了检测和比对，结果表明两步相位相减法矫正相位畸变后的台阶高度和轮廓与粗糙度仪的测量结果具有很好的一致性。

在上述理论分析和实验对比的基础上将实验装置用于微流控芯片通道和缺陷检测，获得了通道的三维形貌，并清晰观察到通道表面断裂型和缺损型缺陷的三维结构，同时测得两种缺陷的宽度和深度信息，研究结果为数字全息显微技术用于微流控芯片的前期加工优化和后续的质量评估提供一定的参考价值。