-
为保证设备正常运行，航行器在水下运动过程中会利用冷却水吸收设备运行所产生的热量，冷却水排出后形成热射流[1-4]并与环境流体掺混换热。热射流向上浮升在水面形成红外特征，易被红外探测设备监测发现。
国内外学者对热射流相关特征进行了大量的实验及仿真研究。Voropayev[4-8]对各类航行器热射流紊流流迹进行了全面而详细的研究，通过实验测量热射流紊流流迹的温度场扩散分布以及速度场矢量分布等射流紊动特征。研究重点分析了热射流的变化特点，并未涉及附体结构对于热射流特征的影响作用。杨卫平等[9]利用等比例缩小水下航行器模型在模拟水池中进行热射流排出的相似实验，保证了结构比例的相似、排放流量的相似从而实现排出热射流温度扩散过程及浮升衰减过程的相似。实验探究了航行器巡航深度、热射流排放速度等影响因素对热射流温度场分布的影响。来庆志[10]通过水槽实验对水下航行器热射流排出过程进行模拟，采用显色剂对热射流紊流流场进行观测，通过这一实验方法详细记录了热射流浮升变化过程。与上述实验不同，文中重点对排放口结构作用下热射流红外特征的变化进行探讨。周哲等[11]采用了不同于来流法的温度差值法来计算热射流温度变化特征，对比了不同工况下热射流温度衰减特征的差异。该研究通过优化仿真方法提高计算的可靠性，对于探讨影响热射流特征变化的因素并不深入。从上述研究中可以看出，有关热射流特征及变化过程的研究十分完善，但未对排放口结构在热射流特征中的影响进行深入研究探讨。
一般来说，水下航行器热射流排放口为圆形结构，圆形排放口制造简单，经济实用。但不同结构排放口是否对热射流特征产生影响，相关研究尚不充足。张健等[12-13]对水下航行器热射流排放口结构形状进行了研究。结果表明在椭圆形排放口作用下，热射流紊流流场出现了变化，轴心最高温度衰减规律也与圆形排放口有所不同。该研究仅简单对比圆形及椭圆形排放口结构作用，并未对椭圆形排放口结构进行深入研究。文中以椭圆形排放口结构为基础，详细探讨不同半径比椭圆形排放口结构对热射流红外特征的影响。周哲[14]等对圆形、长圆形排放口进行了数值模拟，结果表明交叉排列的横向长圆形更有利于增强热射流与环境水体的掺混换热。该文章依旧以圆形排放口结构为基础，未对椭圆形排放口结构进行研究。但上述文章未对椭圆形排放口结构进行深入分析，研究上仍存在不足。另外，与单孔排放口相比，多孔排放口结构可以使得单股热射流分为多股热射流，加强热射流与环境流体掺混换热效果。高猛等[15]对多孔射流的分叉及融合现象做出了详细研究，阐述了多孔结构排放口射流问题的特点。但该研究对多孔结构分孔形状没有进行深入的考虑，其次对分孔分布位置考虑简单。郑亚男等[16]对平板多孔射流形成的旋涡结构特征进行了研究，结果表明，多孔射流的发展变化产生强脉动特性，壁面边界层出现尾迹涡结构。但该研究未对射流温度特性展开探讨。文中重点围绕排放口结构，首先考虑不同半径比椭圆形排放口对热射流红外特征的影响，并进行实验验证；其次对排放口数量及分布方式进行设计，得到最有利于抑制热射流红外特征的排放口结构，提升水下航行器热隐身性能，降低水下航行器被天基或空基红外设备探测到的风险，为工业设计制造提供理论研究思路。
-
流体运动的复杂性是出于流体本身特性所决定的，流体的惯性、流体的可压缩性、流体的黏性等使得如何描述、测量流体运动变得较为困难。再加上流体运动是否为定常或非定常流动，有旋或无旋流动，层流或湍流流动等，这些流动特点同样导致了流体运动的复杂性。根据流体运动的物理特性，数学家和物理学家们以数学表达的形式建立了流体运动的相关方程组用以描述流体运动[17]。
质量守恒方程可表示为：
$$ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial {x_i}}} = 0 $$ (1) 动量守恒方程可表示为：
$$ \begin{split} & \rho \frac{{\partial {u_i}}}{{\partial t}} + \rho {u_j}\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial p}}{{\partial {x_i}}} - \left( {{\rho _0} - \rho } \right){g_i} =\\ & \frac{\partial }{{\partial {x_j}}}\left[ {\mu \left( {\frac{{\partial {u_i}}}{{\partial {u_j}}} + \frac{{\partial {u_j}}}{{\partial {u_i}}}} \right)} \right] - \frac{2}{3}\frac{\partial }{{\partial {x_i}}}\left( {\mu \frac{{\partial {u_j}}}{{\partial {x_j}}}} \right) \end{split} $$ (2) 式中：ρ0为环境流体密度；
$\;\mu $ 为动力粘性系数；${u_i}\left( {i = 1,2} \right)$ 代表了x、y方向上的速度分量。能量守恒方程可表示为：
$$ \rho {c_p}\frac{{\partial T}}{{\partial t}} + \rho {c_p}{u_j}\frac{{\partial T}}{{\partial {x_j}}} = {u_j}\frac{{\partial p}}{{\partial {x_j}}} + \frac{\partial }{{\partial {x_j}}}\left( {\lambda \frac{{\partial T}}{{\partial {x_j}}}} \right) $$ (3) 受温度影响，环境水体密度状态方程可表示为：
$$ \rho (T) = - 6.71 + 9.119T - 0.026\;45{T^2} + 2.399 \times {10^{ - 5}}{T^3} $$ (4) 选择Realizable k-模型将湍流的脉动值附加项与时均值联系起来。
湍动能k方程可表示为：
$$ \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_j}k} \right)}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _{{k}}}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k}{\kern 1pt} {\kern 1pt} + {G_b} - \rho \varepsilon $$ (5) 耗散率ε方程可表示为：
$$ \begin{split} \frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} +& \frac{{\partial \left( {\rho {u_j}\varepsilon } \right)}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _{\text{ε}}}}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \rho {C_1}S\varepsilon - \\ & \rho {{{C}}_{\text{2}}}\frac{{{\varepsilon ^2}}}{{k + \sqrt {\nu \varepsilon } }} + {{{C}}_{{\text{1ε}}}}\frac{\varepsilon }{k}{C_{3\varepsilon }}{G_b} \\ \end{split} $$ (6) 式中：
${G_{{k}}}$ 代表平均速度梯度引起的湍动能；${G_{{b}}}$ 代表浮升影响引起的湍动能；${{{C}}_{{{1ε}}}}{\text{ = 1}}{\text{.44}}$ ；${{{C}}_{\text{2}}}{\text{ = }}1.9$ ；${\sigma _k}{\text{ = }}1.0$ ；${\sigma _{{ε}}}{\text{ = }}1.2$ 。其中
$$ {C_1} = \max \left[ {0.43,\frac{1}{{\eta + 5}}} \right]\text{，} \eta = S\frac{k}{\varepsilon } \text{，} S = \sqrt {2{S_{ij}}{S_{ij}}} {C_{3\varepsilon }} = \tanh \left| {\frac{v}{u}} \right| $$ (7) 式中：v为平行于重力矢量的速度分量；u为垂直于重力矢量的速度分量。
$$ {\mu _t} = \rho {C_\mu }\frac{{{k^2}}}{\varepsilon } $$ (8) 其中
$$ {C_\mu } = \frac{1}{{{A_0} + {A_s}\dfrac{{k{U^*}}}{\varepsilon }}} $$ (9) 其中
$$ {{{A}}_{\text{0}}} = 4.04\text{，} {A_s} = \sqrt 6 \cos \varphi \text{，}{U^*} \equiv \sqrt {{s_{ij}}{s_{ij}} + {{\tilde \varOmega }_{ij}}{{\tilde \varOmega }_{ij}}} $$ $$ \begin{split} & \varphi = \frac{1}{3}{\arccos }\left( {\sqrt 6 W} \right)\text{，} W = \frac{{{s_{ij}} + {s_{jk}} + {s_{ki}}}}{{{{\tilde s}^3}}}\text{，} W = \frac{{{s_{ij}} + {s_{jk}} + {s_{ki}}}}{{{{\tilde s}^3}}}\text{，}\\ & {s_{ij}} = \frac{1}{2}\left( {\frac{{\partial {u_j}}}{{\partial {x_i}}} + \frac{{\partial {u_i}}}{{\partial {x_j}}}} \right) \end{split} $$ 式中：
${\tilde \varOmega _{{{ij}}}}$ 在角速度为$\omega $ 的移动参考系中的平均旋转速率张量。 -
流体计算域长宽高为8 m×1.1 m×0.5 m，水下航行器距离流体计算域左侧来流面100 mm，距离右侧出流面7000 mm，距离底部100 mm，距离顶部300 mm （距离水面200 mm），距离后部300 mm，距离前部700 mm。绘制网格时采用非结构化网格进行划分，在局部尺寸上，对排放口、航行器表面以及局部加密实体区域进行限制，网格类型采用多面体混六面体网格类型。网格划分完成后如图1所示。
图 1 流体计算域网格划分示意图
Figure 1. Grid division schematic diagram of fluid computing domain
-
在边界条件的设置上，排放口为速度入口边界条件（velocity-inlet）；航行器表面为非计算边界条件（dead）；来流面为速度入口边界条件（velocity-inlet）；出流面为压力出口边界条件（pressure-outlet）；流体计算域顶部（top）为压力出口边界条件（pressure-outlet）；流体计算域其余面（wallw）为对称边界条件（symmetry）。来流面设置环境流体来流温度293 K，来流速度0.1 m/s；排放口设置热射流初始温度333 K，热射流初始速度0.3 m/s。
在求解设置中，考虑到水下航行器热射流水面红外特征，文中在流体计算域中划分出空气层，对气液交界层采用VOF流体体积函数进行追踪，水面上的空气层厚度为100 mm。求解方法上文中采用基于有限体积法思想的SIMPLE算法，Solver类型为Pressure-Based，时间属性上采用Transient。同时将重力作用对流体运动的影响体现在求解过程中。关于计算求解的可靠性要求体现在对各参数收敛残差的限制上，能量残差的收敛数量级要小于10−7，其余各参数残差的收敛数量级要小于10−4。计算过程中达到残差收敛要求可认为计算求解结果可靠。
为消除网格数量对计算结果的影响，选取热射流距排放口中心水平距离0.1、0.3、0.5 m处中心最高温度值作为验证数据，对比验证相同位置、不同网格数量条件下，水下航行器热射流中心最高温度。同时，提取水面中轴线上距排放口中心水平距离1.5、2、2.5 m处温度值进行对比。验证结果如图2所示。图中数据表明，当网格数量超过100万时，热射流在距离排放口中心不同距离处中心最高温度值较为一致，误差值较小，在0.01 K以内。因此在设置网格尺寸时，将网格数量控制在150万左右较为合适。
图 2 网格无关性验证
Figure 2. Grid independence test
-
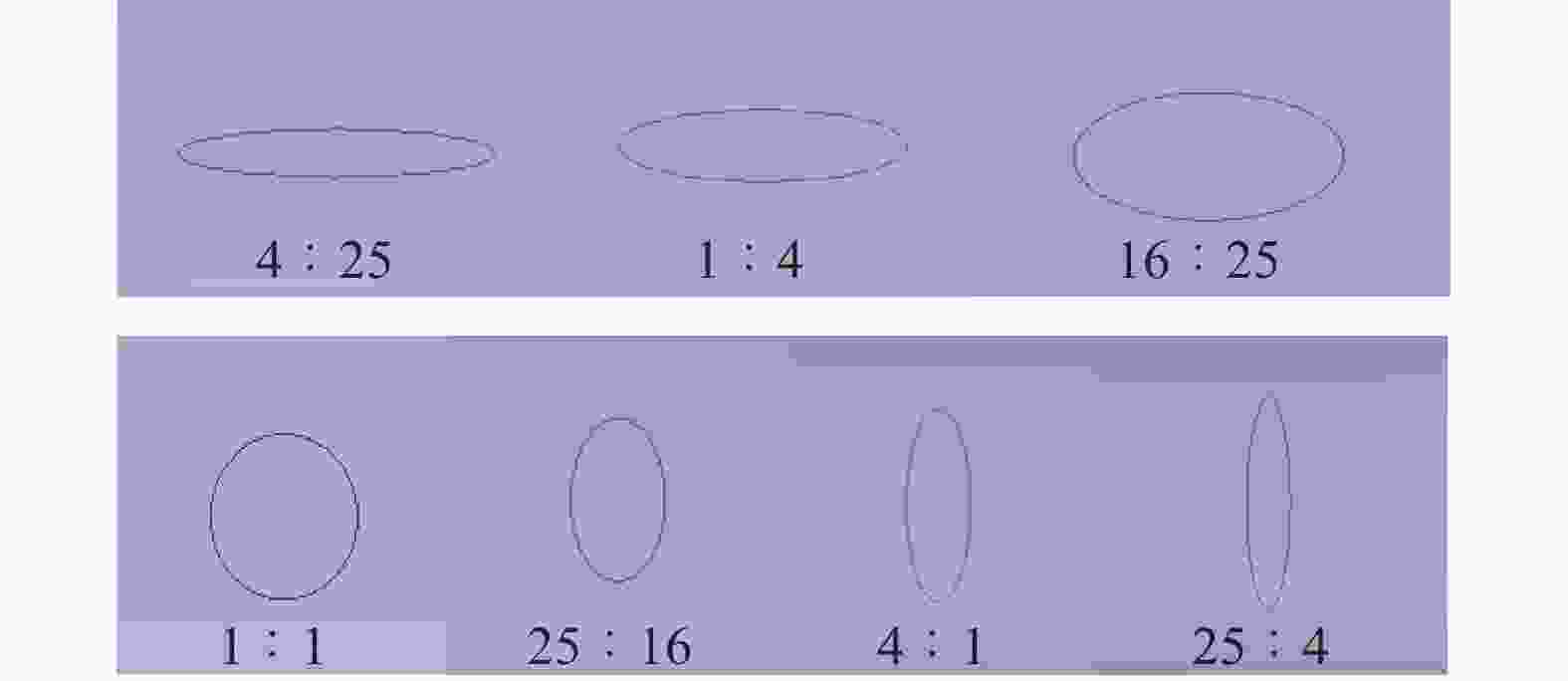
在空间维度中，以排放口中心为坐标原点，环境流体流动方向为X轴负方向，热射流排出方向为Y轴正方向，重力方向为Z轴负方向建立三维直角坐标系。各结构椭圆形排放口长短半径分别沿X轴及Z轴方向分布。定义Z轴上椭圆形排放口半径与X轴上椭圆形排放口半径之比为半径比。表1为不同半径比椭圆形排放口结构参数。各结构椭圆形排放口如图3所示。
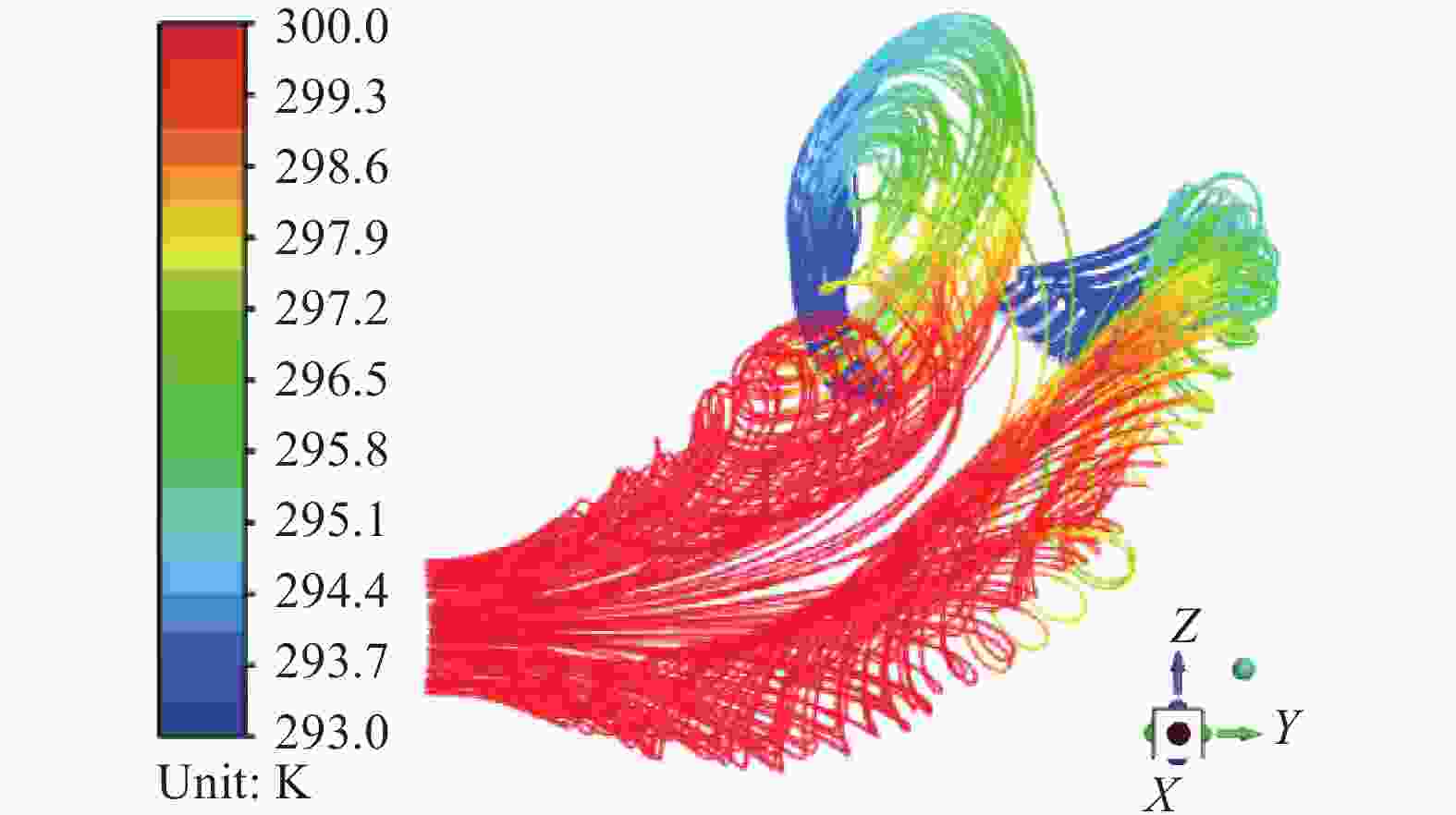
从图4中热射流流迹可以看出，受环境水体运动影响，冷却水排出后出现分流现象，形成两股热射流。其中一股热射流在Z轴方向上浮升较快，但在Y轴方向上运动距离较小；另一股热射流浮升高度较低，但排出的距离较远。由于出口速度较大，热射流在射出一段距离后才开始向后运动，运动状态受航行器壁面影响较小。
表 1 不同半径比椭圆形排放口结构参数
Table 1. Structure parameters of different radius ratio oval discharge ports
Number Radius in Z-axis/m Radius in X-axis/m Radius ratio Str 1 0.004 0.025 4∶25 Str 2 0.005 0.02 1∶4 Str 3 0.008 0.0125 16∶25 Str 4 0.01 0.01 1∶1 Str 5 0.0125 0.008 25∶16 Str 6 0.02 0.005 4∶1 Str 7 0.025 0.004 25∶4 
图 3 不同半径比椭圆形排放口结构示意图
Figure 3. Structure diagram of different radius ratio oval discharge ports
图 4 圆形排放口热射流流迹图
Figure 4. Flow streamline of thermal jet from circle discharge port
从图5中排放口附近流体运动可以发现，来流与冷却水掺混时在排放口后方形成了涡旋运动。由于热射流温度高、速度快，流体压力较小，与排放口后方环境水体产生压力差，由此形成了排放口后方与来流方向完全相反的流体运动。因此，受环境水体逆流运动影响，冷却水在排出后形成两股运动状态不同的热射流。环境水体与热射流之间充分接触掺混，接触面周长即为圆形排放口周长，约62.832 mm。
图 5 圆形排放口热射流局部速度矢量图
Figure 5. Local velocity vector diagram of thermal jet from circle discharge port
图6为热射流排放20 s时水面温度云图，受热射流温度影响，环境水体自由液面形成了部分温度升高区域，温升区域以某一点为中心向四周扩散。由于热射流分流现象的出现，导致水面温升区域存在两个温度中心，水面温度扩散区域以X轴方向上横向扩散为主。水面温升区域在X轴方向上的最大扩散距离为2.138 m，在Y轴方向上的最大扩散距离为0.794 m。
图 6 圆形排放口热射流水面温度分布
Figure 6. Surface temperature contour of thermal jet from circle discharge port
按照相同的模型、相同的网格划分、相同的计算参数设置对不同半径比椭圆形排放口排出热射流过程进行计算。对计算结果进行分析后得到不同半径比椭圆形排放口作用下热射流水面温升区域特征数值。
表2为各半径比椭圆形排放口热射流排放20 s时在水面形成的温度扩散区域相关特征的数值。以圆形（结构4）排放口特征值为标准值，当排放口半径比小于1时，水面最高峰值温度下降，与标准值相比，最大降幅为52.03%。当排放口半径比发生变化，热射流水面温度扩散区域横向扩散最大距离变化不大，纵向扩散最大距离减少25.82%~34.38%。
虽然不同半径比椭圆形排放口面积相同，但是排放口周长不同。其中，结构1与结构7排放口周长最大为241.080 mm，而圆形（结构4）排放口周长最小为62.832 mm。排放口周长越大，热射流在排放口出口处与环境水体的接触面越大，掺混换热效果越好。
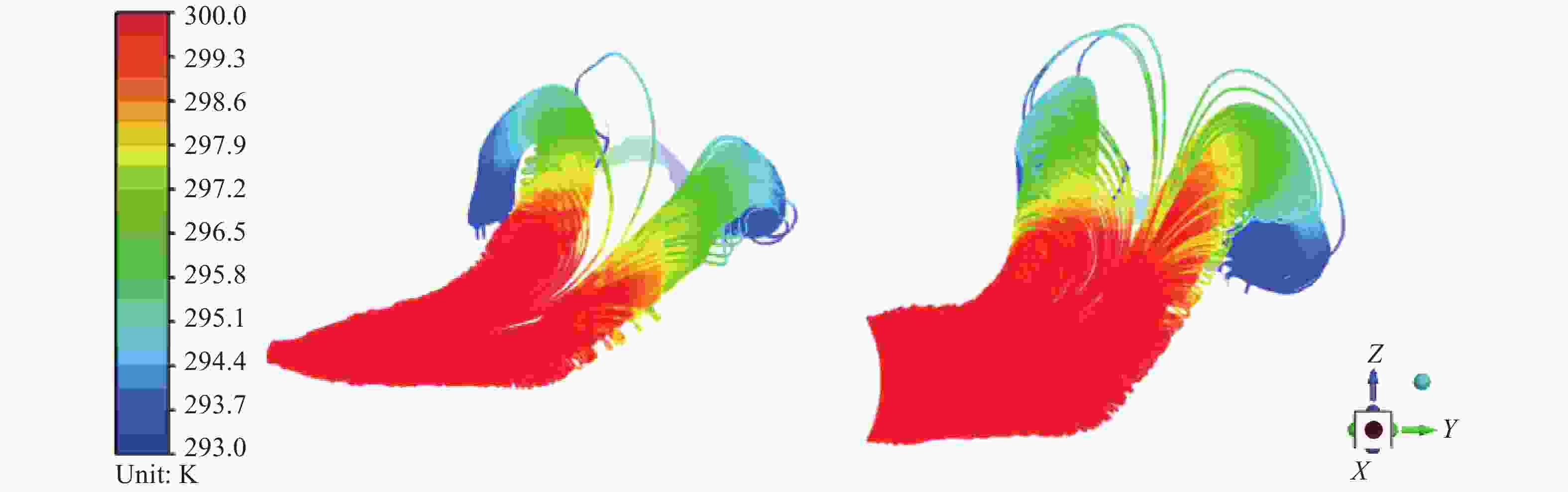
从图7中半径比4∶25和25∶4的椭圆形排放口热射流流迹来看，半径比越小，热射流在出口处宽度越小，热射流温度衰减越快，浮升较快的一股热射流流量也越小。半径比小于1的椭圆形排放口作用下热射流分流现象更加明显，半径比为4∶25时，热射流对水面温升扩散区域的影响小于半径比为25∶4的椭圆形排放口作用。
表 2 不同半径比椭圆形排放口热射流水面温度场特征值
Table 2. Surface temperature value of thermal jet from different radius ratio oval discharge ports
Number Peak temperature/
KDiffusion distance
in X-axis/mDiffusion distance in
Y-axis/mStr 1 293.071 2.152 0.521 Str 2 293.109 2.140 0.580 Str 3 293.101 2.119 0.539 Str 4 293.148 2.138 0.794 Str 5 293.100 2.129 0.541 Str 6 293.152 2.213 0.586 Str 7 293.196 2.333 0.589 
图 7 半径比4∶25、25∶4椭圆形排放口热射流流迹图
Figure 7. Flow streamline of thermal jet from radius ratio 4∶25, 25∶4 oval discharge ports
-
该实验所准备的实验器材大致分为四项：实验水池、水下航行器模型、电驱轨道拖车、红外热像仪及照相设备，如图8~图11所示。
实验水池长7.5 m、宽1 m、高1 m。水池底部有两个入水口和一个排水口，入水口进水流量为2084 cm3/s，出水口排水流量为695 cm3/s。水下航行器模型长0.591 m，最大直径0.061 m，排放口位于水下航行器中心后0.150 m处。电驱轨道拖车位于水池上方，拖车通过控制箱调节速度，带动水下航行器在水池中直行，拖车运动速度即水下航行器航行速度。拖车上方设置有水箱，增压泵，流量调节阀等。通过控制阀门开度调整水流进入水下航行器模型的速度，从而调整热射流排放速度。
图 8 实验示意图
Figure 8. Experimental diagram
图 9 实验水池
Figure 9. Experimental pool
图 10 拖车控制器
Figure 10. Controller of trailer platform
图 11 水下航行器模型
Figure 11. Model of underwater vehicle
将水下航行器模型置于水池中，航行器位于水面0.02 m以下，航行器通过铁管与拖车上方管道连接水箱，水箱内热水经由排放口排出，与水池内室温状态下的环境水体掺混换热。热水温度保持与环境水体温度相差40 ℃。水箱内加入黑色示踪剂体现热射流运动状态。同时通过控制箱启动拖车在轨道上直行带动航行器运动，模拟航行器航行状态。在水池一侧利用红外热像仪对水池水面温度场进行测量，测量热射流水面红外特征。
图12中热射流随时间变化在环境水体中不断扩散，热射流与环境水体的温差使得两类流体之间密度不同，热射流密度较小，受浮力作用向上浮升。初期热射流向上浮升不明显，经过一段时间的运动，热射流向上浮升至接近水面，热射流宽度随着排出距离的增加越来越大。
图 12 圆形排放口热射流运动扩散轨迹
Figure 12. Trajectory of thermal jet from circle discharge port
图13中受热射流影响，水面形成部分温升区域，与仿真结果不同在于，实验环境下水面温度扩散不均匀、不连续，但仍然以运动方向上的扩散为主，水面最大温差也较低。
图 13 圆形排放口热射流水面温度场
Figure 13. Surface temperature contour of thermal jet from circle discharge port
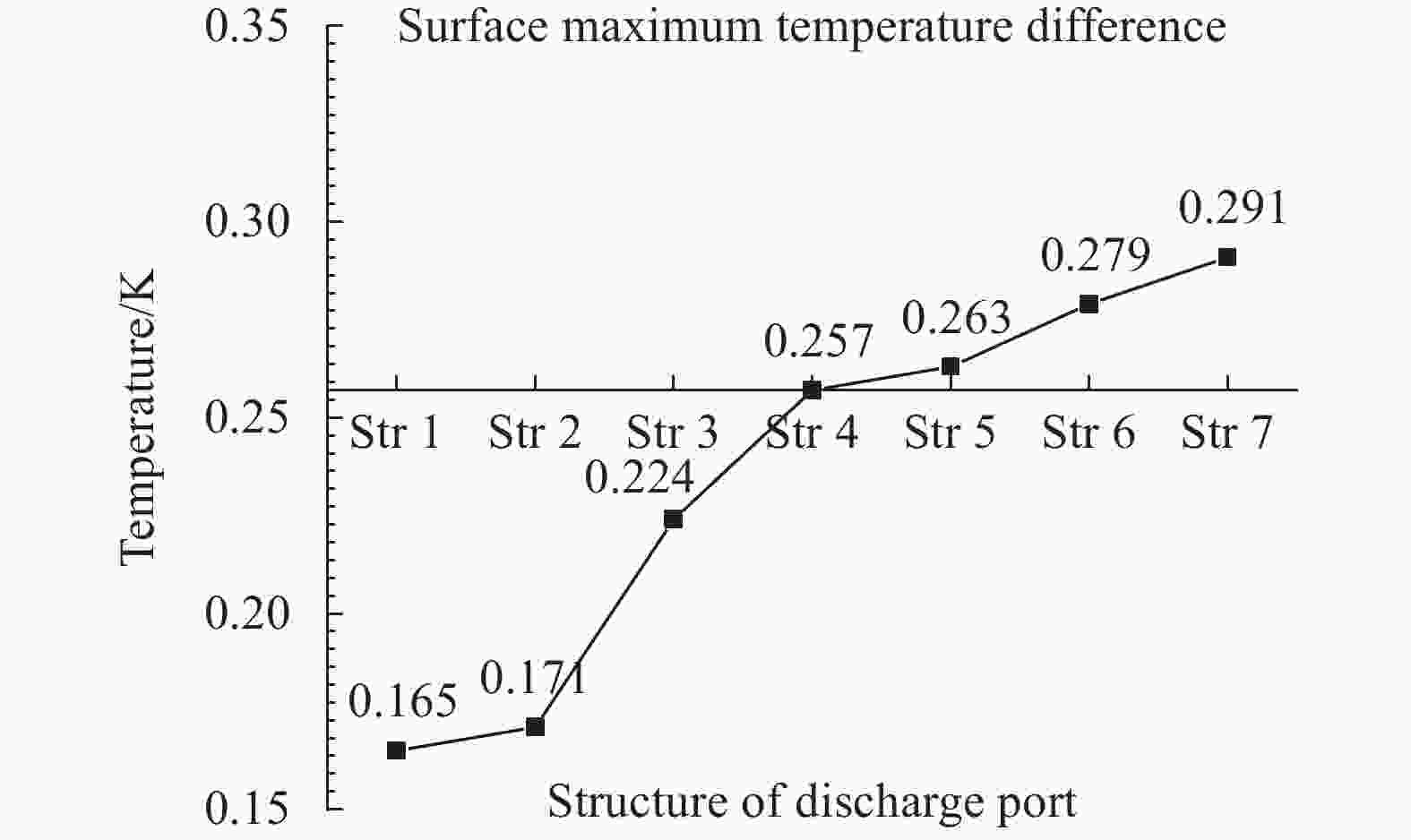
在相同的实验条件下，对比不同半径比椭圆形排放口热射流水面温度最大温差如图14所示。与圆形（结构4）排放口相比，排放口半径比小于1时，水面最大温差下降，降幅在12.84%~35.80%之间；半径比大于1时，水面最大温差增加。
通过实验证明，改变排放口半径比对于热射流在水面形成的温度扩散区域有较为明显的影响。实验所得结论与仿真计算结论较为一致，降低排放口半径比有利于加强热射流与环境流体掺混换热，抑制热射流水面红外特征。
图 14 不同半径比椭圆形排放口热射流水面最大温差
Figure 14. Surface maximum temperature difference of thermal jet from different radius ratio oval discharge ports
-
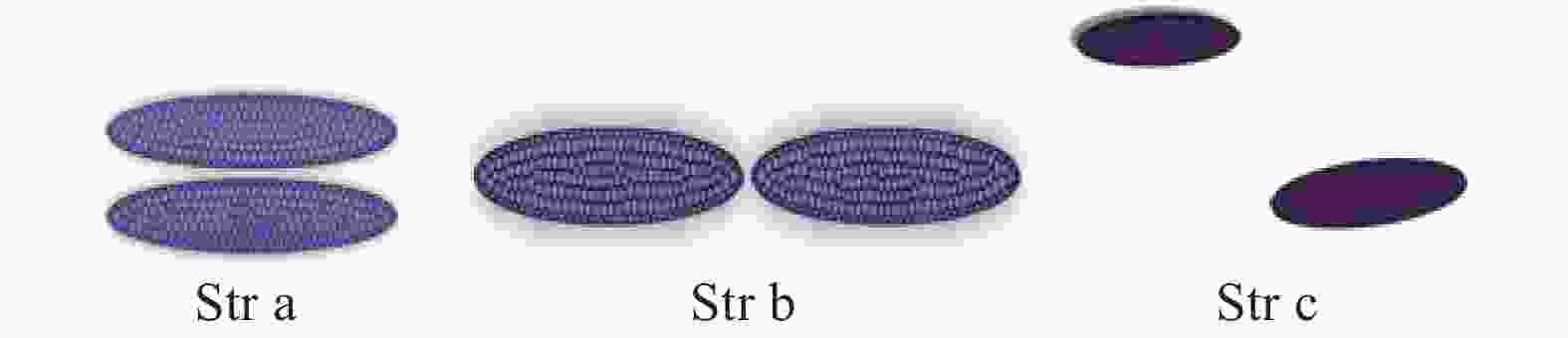
由仿真及实验结果可知，当椭圆形排放口半径比为4∶25时，排放口周长最大，Z轴半径最小，热射流宽度最小，热射流与环境流体掺混换热效果最好。因此，在结构1椭圆形排放口的基础上，保持排放口总面积不变，增加排放口数量，调整排放口分布位置，保证分孔排放口半径比不变。具体排放口结构如图15所示。
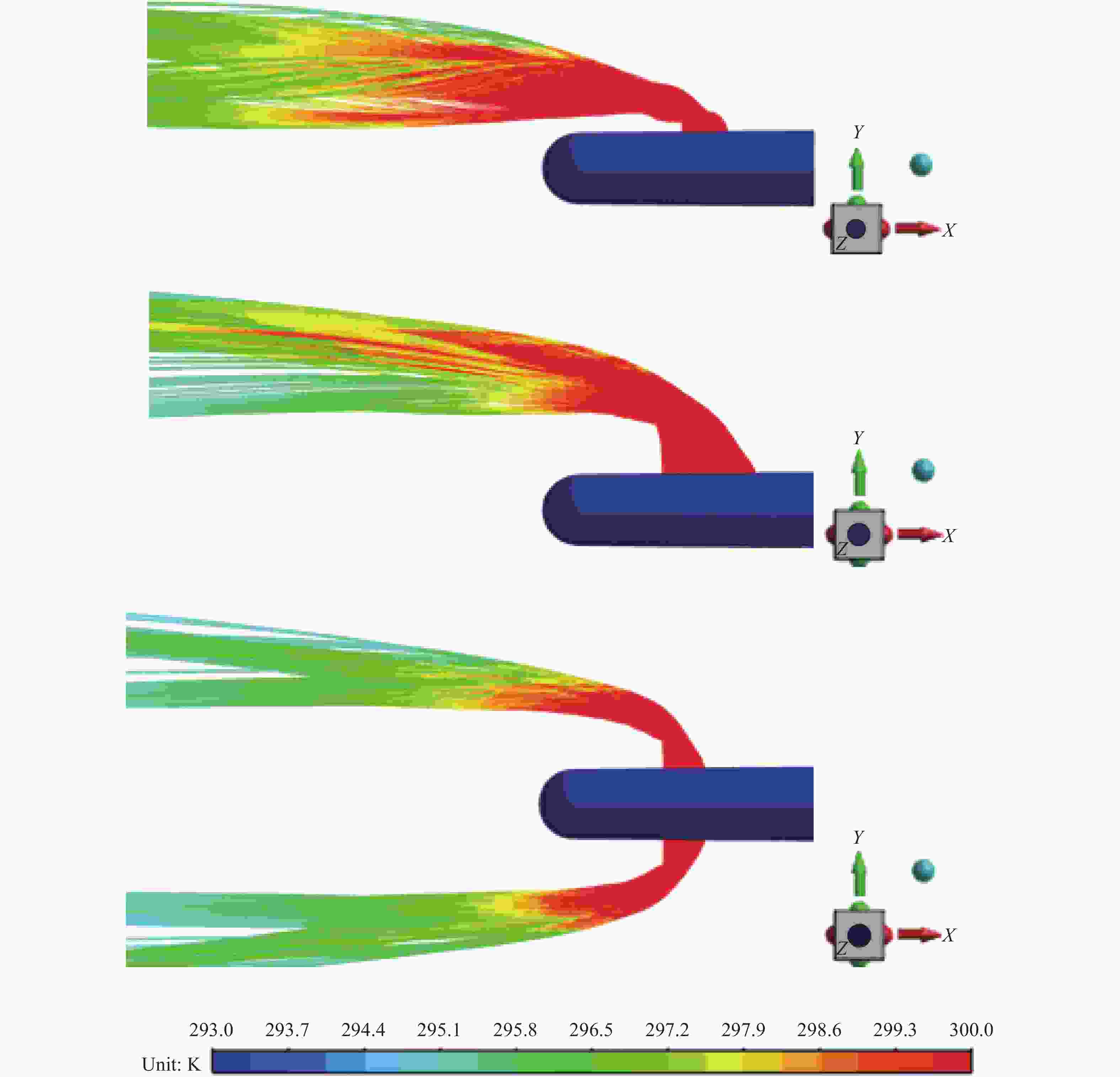
从图16中可以看出，当排放口位于水下航行器一侧时，分孔热射流之间会产生卷吸掺混现象，不利于热射流温度迅速下降。当两个排放口上下分布时，热射流动量损失迅速，速度损失大，与环境水体掺混效果较差。当两个排放口前后分布时，热射流在初始运动方向上运动距离增大，温度下降迅速，与环境水体掺混换热效果好。当两个排放口位于航行器两侧时，热射流温度下降最快。排放口分孔热射流之间没有卷吸现象，有利于提升热射流与环境水体掺混换热效果。
图 15 多孔排放口结构示意图
Figure 15. Structure of discharge multiport
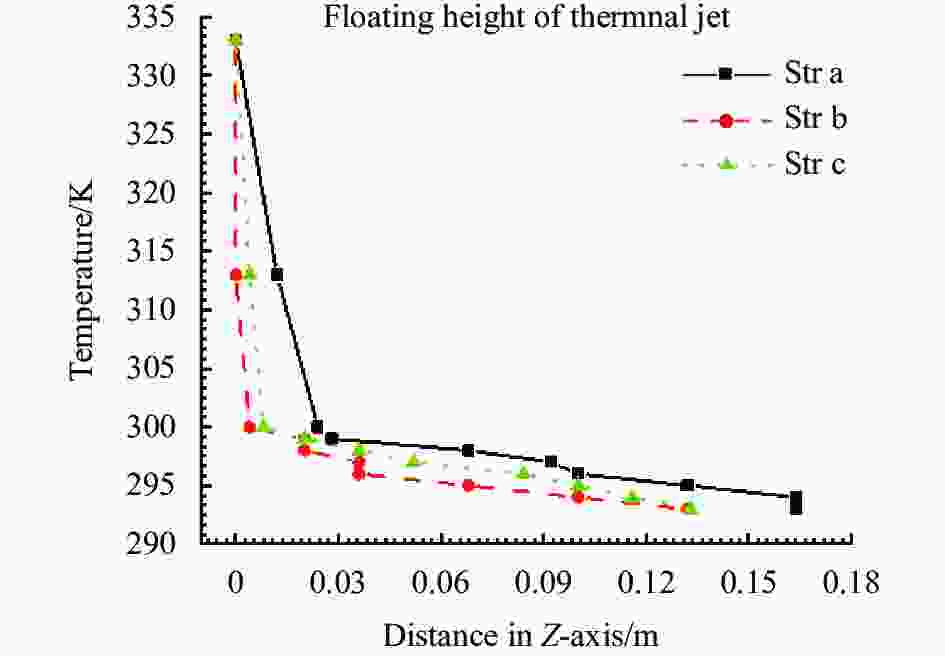
图17为各多孔排放口热射流浮升高度变化曲线。从图中可以看出，结构a排放口热射流浮升较快，热射流温度下降较慢，而结构b与结构c排放口热射流温度衰减较快，浮升高度也较低。与单孔半径比4∶25椭圆形排放口相比，结构a排放口热射流对水面温度影响增强，水面最大温差为0.128 K。而结构c排放口热射流在水面形成的温度中心最大温差为0.052 K，热射流红外特征减弱。
图 16 多孔排放口热射流流迹图
Figure 16. Flow streamline of thermal jet from discharge multiport
图 17 多孔排放口热射流浮升高度
Figure 17. Floating height of thermal jet from discharge multiport
-
文中通过仿真结合实验的方法探究水下航行器排放口结构对热射流红外特征的影响。设计椭圆形排放口，改变排放口半径比，增加排放口接触面周长。同时进一步设计多孔排放口，增加排放口数量，调整排放口分布位置。根据研究结果可以得到如下结论：
(1)排放口半径比越小，热射流掺混接触面大，热射流掺混换热效果越好，热射流红外特征越不明显。
(2)排放口Z轴半径越小，热射流在出口处宽度越窄，热射流浮升高度越低。
(3)增加排放口数量，减小排放口间隙有利于加快热射流温度衰减过程，降低热射流在水面形成的温度中心最大温差。
(4)当排放口分布在水下航行器两侧时，排放口之间卷吸掺混现象消失，热射流温度衰减过程加快，在水面形成的温度扩散区域特征也越不明显。
(5)排放口结构对热射流红外特征具有明显影响，改变排放口形状、数量、分布位置有利于提升水下航行器热隐身性能。
Influence of the discharge port structure on infrared characteristics of underwater vehicle thermal jet
-
摘要: 水下航行器动力系统循环冷却水经由排放口排出，与环境水体掺混换热形成热射流。热射流在环境水体中扩散、浮升并在水体表面形成红外特征。为探究排放口结构对水下航行器热射流红外特征的影响，文中采用仿真分析结合实验验证的方法进行研究。依托CFD计算软件平台建立水下航行器运动模型，设计不同半径比椭圆形排放口结构并对比热射流红外特征差异。通过缩比水池实验验证椭圆形排放口半径比对热射流红外特征的影响，同时验证仿真计算方法及设计参数的有效性。在椭圆形排放口的基础上，进一步设计排放口数量及分布位置，抑制热射流红外特征，提升水下航行器热隐身性能。根据仿真计算及实验结果可知，在排放流量相同的条件下，半径比越小的椭圆形排放口热射流掺混换热效果越好，红外特征越不明显。同时，增加排放口数量以及排放口分布位置采用两翼排列方式可以进一步加强热射流温度衰减，降低水面最高峰值温度。Abstract: The circulating cooling water of the underwater vehicle power system discharged from the discharge port, mixed with the environmental water for heat exchange and formed the thermal jet. The thermal jet diffused and floated in the environmental water and forms infrared characteristics on the surface of the water. In order to explore the influence of the structure of the discharge port on the infrared characteristics of the underwater vehicle thermal jet, this paper used the method of simulation analysis and experimental verification. Based on the CFD calculation software platform, the motion model of underwater vehicle was established, the structure of different radius-ratio oval discharge ports was designed, and the infrared characteristics of thermal jet were compared. The influence of the radius ratio of the oval discharge port on the infrared characteristics of the thermal jet was verified by the scale tank experiment, and the authenticity of the simulation calculation method and design parameters was verified at the same time. On the basis of oval discharge ports, the number and distribution position of discharge ports were further designed to suppress the infrared characteristics of thermal jet and improve the thermal stealth performance of underwater vehicles. According to the simulation calculation and experimental results, under the condition of the same discharge flow, the smaller the radius ratio was, the better the mixed heat transfer effect of the oval discharge port was, and the less obvious the infrared characteristics were. At the same time, increasing the number of discharge ports and adopting the symmetrical arrangement of discharge ports could further strengthen the temperature attenuation of thermal jet and reduce the surface maximum temperature.
-
Key words:
- underwater vehicle /
- thermal jet /
- discharge port /
- structure design /
- infrared characteristics
-
图 3 不同半径比椭圆形排放口结构示意图
Figure 3. Structure diagram of different radius ratio oval discharge ports
图 5 圆形排放口热射流局部速度矢量图
Figure 5. Local velocity vector diagram of thermal jet from circle discharge port
图 6 圆形排放口热射流水面温度分布
Figure 6. Surface temperature contour of thermal jet from circle discharge port
图 7 半径比4∶25、25∶4椭圆形排放口热射流流迹图
Figure 7. Flow streamline of thermal jet from radius ratio 4∶25, 25∶4 oval discharge ports
图 13 圆形排放口热射流水面温度场
Figure 13. Surface temperature contour of thermal jet from circle discharge port
图 14 不同半径比椭圆形排放口热射流水面最大温差
Figure 14. Surface maximum temperature difference of thermal jet from different radius ratio oval discharge ports
表 1 不同半径比椭圆形排放口结构参数
Table 1. Structure parameters of different radius ratio oval discharge ports
Number Radius in Z-axis/m Radius in X-axis/m Radius ratio Str 1 0.004 0.025 4∶25 Str 2 0.005 0.02 1∶4 Str 3 0.008 0.0125 16∶25 Str 4 0.01 0.01 1∶1 Str 5 0.0125 0.008 25∶16 Str 6 0.02 0.005 4∶1 Str 7 0.025 0.004 25∶4 
下载: 导出CSV
表 2 不同半径比椭圆形排放口热射流水面温度场特征值
Table 2. Surface temperature value of thermal jet from different radius ratio oval discharge ports
Number Peak temperature/
KDiffusion distance
in X-axis/mDiffusion distance in
Y-axis/mStr 1 293.071 2.152 0.521 Str 2 293.109 2.140 0.580 Str 3 293.101 2.119 0.539 Str 4 293.148 2.138 0.794 Str 5 293.100 2.129 0.541 Str 6 293.152 2.213 0.586 Str 7 293.196 2.333 0.589
下载: 导出CSV
-
[1] Chevary R. Tutu H K. Intermittrly and preferential transport of heat in a round jet [J]. Fluid Mech, 1978, 88(1): 133-160. [2] Garret W D, Smith P M. Physical and chemical factors affecting the thermal IR imagery of ship wakes(AD-A144034)[R]. Washington DC: Naval Research Lab, 1984. [3] Peltzer R, Garrett W, Smith P. A remote sensing study of a surface ship wake [J]. International Journal of Remote Sensing, 1985, 8(5): 689-704. [4] Chen C J, Singh K. Development of a two-scale turbulence model and prediction of buoyant shear flows[C]//AIAA Thermophys and Heat Transfer Conf. Heat Transfer in Turbulent Flows, 1990, 138: 53. [5] Voropayev S I, Fernando H J S, Smirnov S A, et al. On surface signatures generated by submerged momentum sources [J]. Physics of Fluids, 2007, 19(7): 465. [6] Voropayev S I, Fernando H J S, Nath C. Thermal and dynamic surface signatures of the wake of a submerged sphere [J]. Journal of Visualization, 2009, 12(4): 285. doi: 10.1007/BF03181868 [7] Voropayev S I, Nath C, Fernando H J S. Thermal surface signatures of ship propeller wakes in stratified waters [J]. Physics of Fluids, 2012, 24(11): 466-469. [8] Voropayev S I, Nath C, Fernando H J S. Surface signatures of submerged heated jet [J]. Environ Fluid Mech, 2014, 14(5): 1105-1121. doi: 10.1007/s10652-013-9301-8 [9] Yang Weiping, Zhang Zhilong, Li Jicheng, et al. Thermal wakes detectability of submerged objects based on scale model [J]. Infrared and Laser Engineering, 2016, 45(3): 0302002. (in Chinese) [10] Lai Qingzhi. Study of infrared radiative characteristics of nuclear-powered submarine’s thermal wake[D]. Harbin: Harbin Institute of Technology, 2017. (in Chinese) [11] Zhou Zhe, Bai Zongliang, Shi Jingcheng, et al. The study on thesimulation method based on temperature interpolation technology for the buoyancy law and ocean-surface thermal characteristic of submarine wake [J]. Infrared Technology, 2019, 41(11): 1039-1046. (in Chinese) [12] Zhang Jian, Yang Li, Zhang Shicheng, et al. Temperature characteristic of horizontal heated water jets in the flow [J]. Huazhong University of Science and Technology (Natural Science Edition), 2011, 39(8): 62-66. (in Chinese) [13] Zhang Jian, Yang Li, Zhang Shicheng, et al. Three-dimensional numerical simulation of horizontal circle heated water jets in the flow [J]. Advances in Water Science, 2011, 22(5): 668-672. (in Chinese) [14] Zhou Zhe, Bai Zongliang, Zhao Detao, et al. Structure optimization and simulation analysis of submarine discharge port based on CFD [J]. Ship Science and Technology, 2020, 42(5): 66-70. (in Chinese) [15] Gao Meng, Huai Wenxin, Zeng Yuhong. Dilution characteristics of vertical multiple jets in crossflow [J]. Huazhong University of Science and Technology (Natural Science Edition), 2018, 46(6): 94-98. (in Chinese) [16] Zheng Yanan, Wang Guoyu, Lu Yafei, et al. Study on the flow field characteristics of multiple jets under the flat surface[C]//Proceedings of the 32nd National Conference on Hydrodynamics, 2020. (in Chinese) [17] Bae Y Y, Kim E S, Kim M. Assessment of low-Reynolds number k-ε turbulence models against highly buoyant flows [J]. International Journal of Heat and Mass Transfer, 2017, 108: 529-536. -
点击查看大图
计量
- 文章访问数: 93
- HTML全文浏览量: 22
- PDF下载量: 46
- 被引次数: 0
