-
在激光驱动惯性约束核聚变(Inertial Confinement Fusion, ICF)中,激光辐照强度的均匀性是至关重要的。激光辐照强度的不均匀性,可按空间频率分为低、中、高频不均匀性[1]。其中,低频不均匀性将导致不同位置靶丸燃料内爆的速度不同,从而引起流体不稳定性使靶丸偏离球型,最终导致燃料压缩不充分[2]。而中高频不均匀性能通过印痕效应为流体不稳定过程提供种子[3];能导致等离子体不稳定性[4],包括成丝不稳定性,生成超热电子并影响激光吸收的受激拉曼散射(Stimulated Raman Scattering, SRS),导致反向散射的受激布里渊散射(Stimulated Brillouin Scattering, SBS)等。为了抑制这些不稳定过程,直接驱动要求在空间上,模数在10~20之间的辐射压不均匀性控制优于1%~2%[5];在时间上,为了控制印痕效应和激光等离子体不稳定性(Laser Plasmas Instability, LPI)过程,激光辐照的不均匀性应当在几皮秒内迅速下降。实际的高功率激光受放大、传输和终端光路中多种因素(元件面型、热畸变、气流扰动、损伤点等)影响,其焦斑形态不均匀且不稳定,不符合ICF对激光驱动的要求。为了得到稳定、均匀的焦斑,人们提出了多种束匀滑方法。按照基本原理的不同,可以分为空间域匀滑方法和时间域匀滑方法。
-
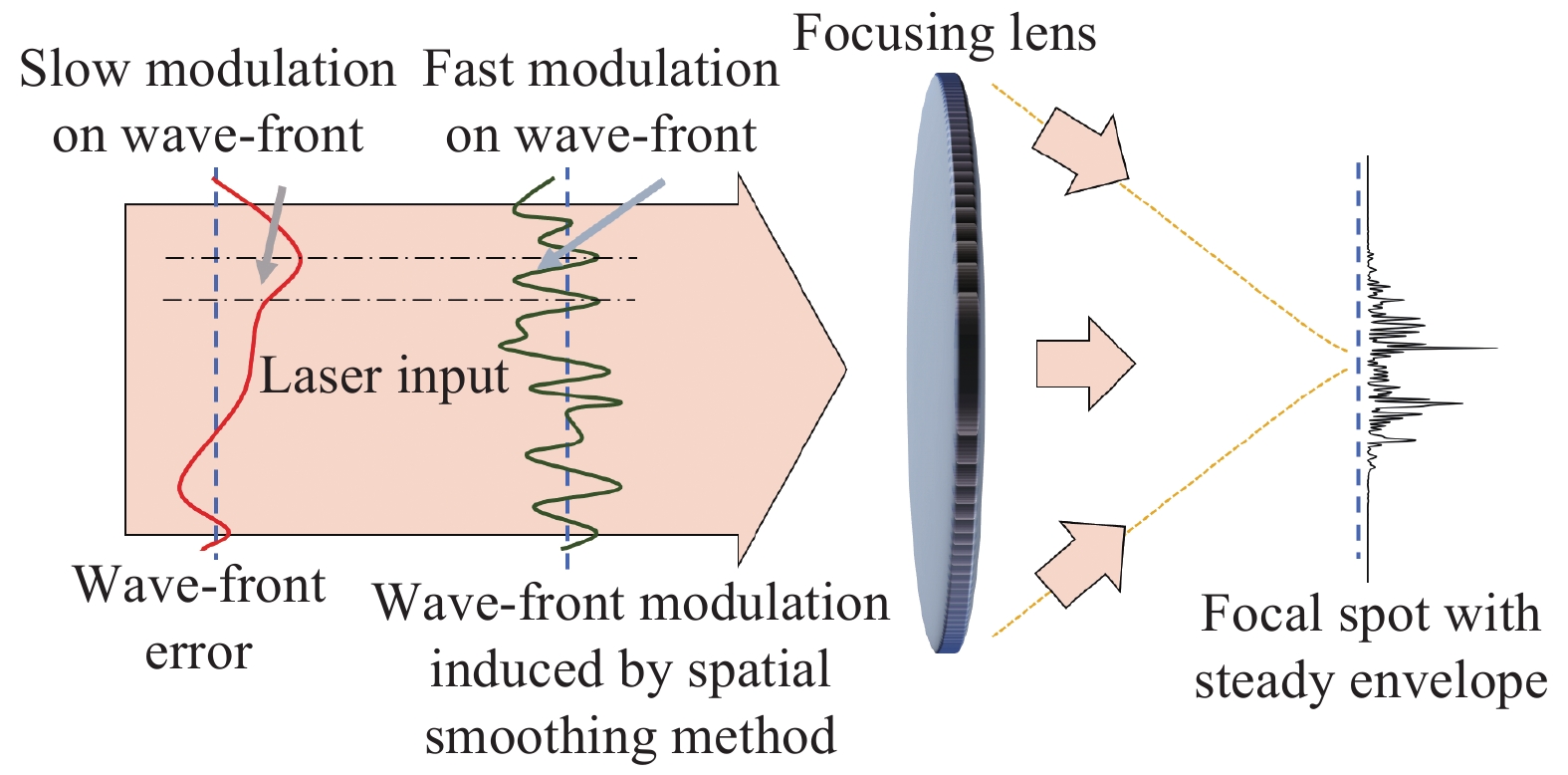
空间域匀滑方法主要指通过相位调控获得具有指定包络形态的焦斑的方法。简单的离焦也能够改变激光光斑形态,然而这种方法得到的焦斑受波前畸变影响较大,并且不能完全改变光斑形态。空间域匀滑的基本物理思想是通过控制波前形态进而控制焦斑,如图1所示。整体上,根据菲涅尔衍射公式,激光焦斑形态与近场分布互为傅里叶变换,因此可以通过近场波面整体形态的改变从而控制焦斑形态。而局部来看,为了减弱波前畸变的影响,所引入的波前调控必须使在特征尺度内,波前畸变能够被忽略,这要求空间域匀滑方法所引入的相位变化梯度(Gradient Root Mean Square, GRMS)大于波前畸变的GRMS。实际焦斑是理想焦斑和波前畸变点焦的卷积,只要使用空间域匀滑后的理想焦斑具有足够尺寸,波前畸变对焦斑包络的影响就不明显。空间域匀滑方法主要包括连续相位板(Continuous Phase Plate, CPP)、透镜阵列(Lens Array, LA)。
-
连续相位板(CPP)[6]能够灵活地调整焦斑形态,被广泛应用于高功率激光装置中。CPP的具体问题是在互为傅里叶变换对的近场和远场强度分布已知的条件下,如何恢复出近场和远场的相位分布。典型的CPP面型如图2所示。通过磁流变抛光[7]、等离子体刻蚀等方式可以将设计的相位分布加工为透射元件的面型分布,进而作用在激光光束上。
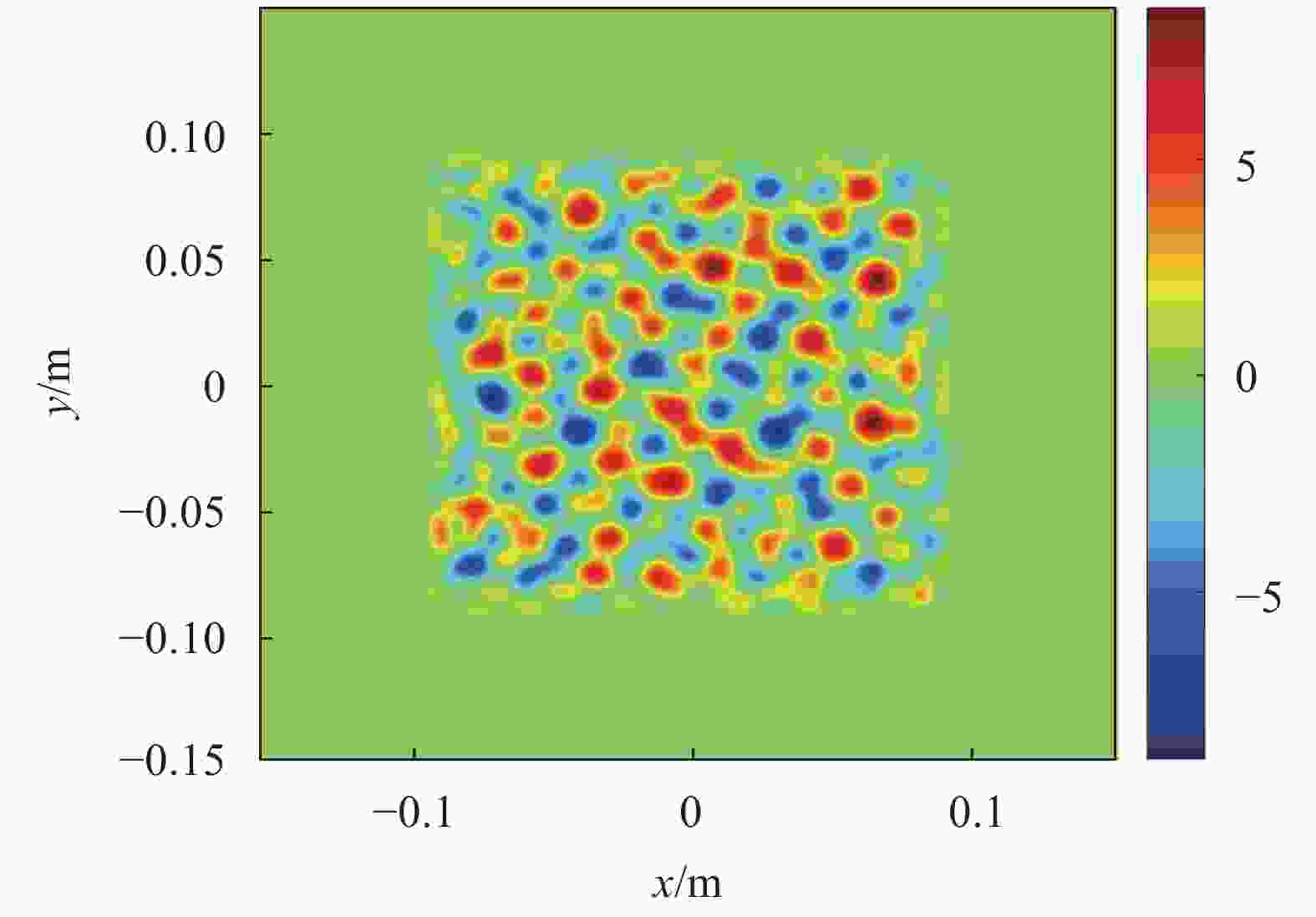
Figure 2. Demonstration of continuous phase plate (CPP). The CPP could obtain circular focal spot with diameter of 32 times of diffraction limitation
1978年,Kato等提出了随机相位板[8](Random Phase Plate, RPP),RPP一般由几百个0或π相位延迟的小块随机排布而成,能够获得具有高斯型包络的焦斑,并且对波前畸变不敏感。然而RPP存在着衍射效率低、焦斑形态不可控等问题。1994年,Dixit等提出了基于Gerchberg-Saxton (G-S)算法[9]的相息相位板(Kinoform Phase Plate, KPP)[10]作为RPP的改进,获得了焦斑包络控制的能力;然而其结果中存在不连续线,无法实际制作,并导致部分能量被散射到焦斑之外,成为噪声。1995年,Lin等[11]报道了利用G-S算法获得的分布相位板(Distributed Phase Plate, DPP),利用空间周期变化的傅里叶光栅和随机相位组合作为迭代的初始面型,并控制迭代次数,大幅度减少了相位板中的奇点。1996年Dixit等[6]提出在G-S算法中,通过控制远场缓变避免出现相位奇点,从而获得了完全连续的相位板。2003年Neauport等[12]报道了LMJ上基于改进G-S方法的设计结果,通过强制相位分布缓慢变化避免了不连续线的产生,此外还使用了额外的远场补偿以减弱大尺度的焦斑不均匀性。2007年Marozas[13]提出了一种改进的G-S方法,通过滤波和解包算法,获得了具有高通特性的CPP (High-pass CPP),其远场包络形态与目标函数符合较好,同时低频不均匀性能够得到一定程度的抑制;2016年Marozas等[14]在一篇会议报告上,给出了在具有波前畸变的情况下的焦斑PSD,结果表明此时的High-pass CPP相比于Goodman散斑模型[15],仍然具有较低的中低频不均匀性。2008年,李平等[16]提出了另一种改进G-S算法,在迭代中加入了权重因子以保证相位分布缓慢变化,通过迭代前后的相位差与2π的大小关系直接判断相位变化,进而简化解包过程。2016年,雷泽民等[17]提出了用光场传输公式替换G-S方法中的傅里叶变换的改进方法,该方法能够灵活改变目标面位置、分辨率,代价是计算量的大幅度增加。
光束经过CPP调制后,近场将随传输而发生强度调制。2011年温圣林等[18]人分析了光束经CPP前后面干涉和传输对近场均匀性的影响,指出为了控制CPP后的近场调制度,需要对CPP镀增透膜,并保证传输距离小于1.5 m。
CPP的设计属于相位恢复问题的一种。更深入的CPP设计理论有望在信息光学、全息术等领域获得应用,仍然有待人们进一步研究。
-
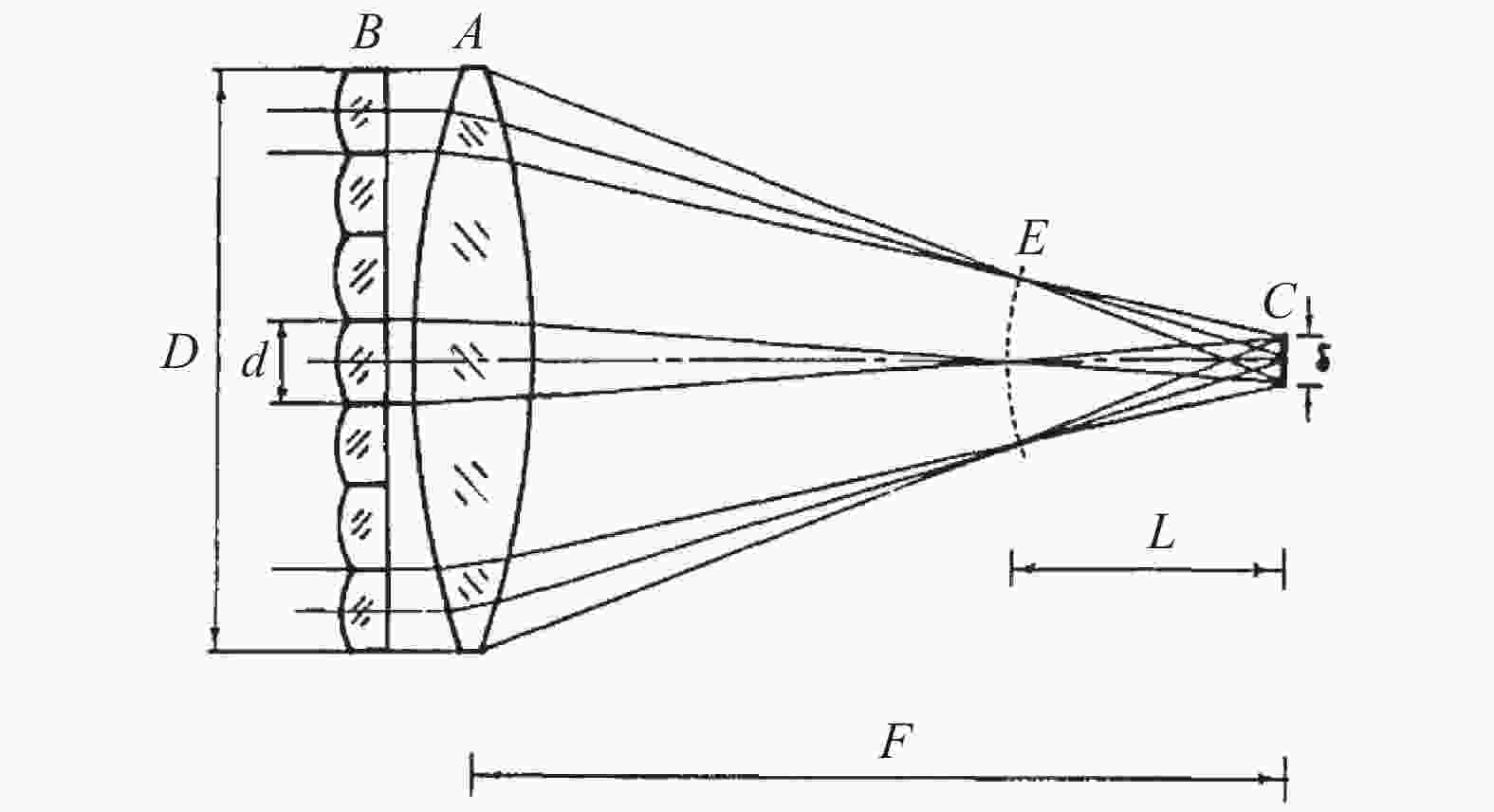
1986年,邓锡铭等[19]提出了透镜阵列(LA)用于高功率激光焦斑的形态控制,其原理如图3所示。光束分为子束,经过透镜阵列子透镜和主透镜后,其理想焦点前移至E面上,在主透镜焦平面C面上形成准近场光斑。不同子束在C面上相干叠加,最终获得具有周期调制散斑的准近场图样。理想情况下,LA焦斑可用LA子束的准近场分布Es表示:
式中:j,k是LA子束的编号;Tj,k是编号为j,k的子束的近场位移矢量;r是远场坐标。D(r)的形式被称为二维Dirichlet核,其形态类似于二维梳状函数,其单个周期的形态类似于sinc函数。根据函数D(r)的性质,LA方法的散斑尺度由全光束衍射极限决定,而散斑空间间隔由子透镜衍射极限决定,理论上其焦斑强度峰值将大大高于CPP散斑,然而因光学系统波前畸变的影响,实际上两者差别不大。此外LA使用时一般会适当离焦,使不同子束的菲涅尔衍射包络交错开,这也会改变散斑形态,但一般不会改变其周期性。
2007年,郑建洲等[20]提出了焦斑可调的LA模式,使用了额外的透镜阵列,通过改变两组透镜阵列、主透镜之间的距离控制焦斑的尺寸,分析表明这种方法能够获得mm到百μm量级的可调焦斑,能够满足ICF的焦斑尺寸需求。
-
空间域方法的使用能够改善激光能量沉积的大尺度均匀性,一般认为等离子体热传导能够大幅度减弱能量沉积的高频不均匀性。然而印痕阶段,尚未生成足够密度的等离子体,此时的高频不均匀性将直接影响靶丸的外表面形态,成为RT不稳定性的种子[21]。此外,激光等离子体不稳定性也会受到高频不均匀性的影响[22]。因此高频不均匀性的控制仍然是必要的。然而激光的高频不均匀性即激光散斑,无法彻底消除[23]。只能通过降低激光的空间相干性,在足够积分时间后减弱激光散斑。因此时间域方法通过对光束近场相干性进行调控从而控制焦斑相干性,进而降低高频不均匀性。
时间域匀滑方法的原理如图4所示,空间低相干光的瞬时波面随时间不断变化,从而获得动态的焦斑,并在足够积分时间后减弱焦斑中的散斑。相干性的降低依赖于引入带宽,带宽小于激光带宽的不稳定过程可以通过时间域匀滑方式得到抑制[24]。然而LPI的抑制除了受到激光带宽影响外,还依赖于激光调制的形式。激光带宽并不能直接改变焦斑形态,宽带激光如果具有高空间相干性,则焦斑仍然会存在稳定的随机散斑,而这些随机散斑将引起成丝不稳定性进而引起SBS、SRS等其他LPI过程[25]。成丝不稳定性的抑制需要激光散斑在几十ps内迅速变化,并具有均匀的时间积分效果。这除了需要足够激光带宽以外,还需要合理设计时间域匀滑方法才能实现这种效果。典型的,单调制的谱色散匀滑方法即使获得1 THz量级的激光带宽[26],但因其时空调制速度较慢,焦斑匀滑速度慢于同带宽下的理想随机时空散斑匀滑速度。
一般认为散斑演化的特征时间Tc~1/Δν[27],基于随机散斑假设,可以获得焦斑不均匀性的时间演变公式[27-29]:
式中:σ0表示初始焦斑强度分布的均方根(Root Mean Square, RMS);σinf表示无穷长积分时间后的焦斑RMS;σT表示T积分时间后的焦斑RMS。由公式(2)可知,焦斑不均匀性降低的速度取决于相干时间,即激光带宽。公式(2)基于焦斑演化完全随机的假设,但多数束匀滑方案的焦斑演化并不是完全随机的,这导致实际的焦斑不均匀性降低速度较慢,散斑演化的特征时间也偏大。单纯从焦斑匀滑速度来看,这种情况下激光的带宽实际上并没有完全得到利用。
时间域束匀滑方法主要包括:偏振匀滑(Polarization Smoothing, PS),诱导空间非相干(Induced Spatial Incoherence, ISI),角色散匀滑(Angular Dispersion of the Spectrum, ADSP),谱色散匀滑(Smoothing by Spectral Dispersion, SSD),径向匀滑(Radial Smoothing, RS),角向匀滑(Azimuthal Smoothing, AS),随机脉冲序列(Spike Train of Uneven Duration and Delay, STUD)。这些方法多数无法控制焦斑形态,因此一般与空间域方法联合使用。
-
偏振匀滑(PS)[30]通过两种偏振光束的组合使用减弱焦斑中的散斑。两种偏振的焦斑不相干叠加,从而使瞬时散斑的RMS下降至0.707倍;此外PS方法的焦斑偏振具有一定的空间分布。物理实验证明PS方法能够抑制SBS和SRS[31]。虽然PS也通过降低光场相干性来减弱散斑,但它并不是一般意义上的时间域方法,其匀滑效果与时间无关。PS可以分为偏振控制板(Polarization Control Plate, PCP)和双折射楔(Birefringent Wedge, BW)[32]两种方案。
偏振控制板(PCP)由Tsubakimoto等[30]于1992年提出。类似于随机相位板,PCP也需要对光束近场分块,并分别使用1/2波片调整偏振方向,从而使子光束之间的可干涉数目减少一半。如图5(a)所示,方形近场被分割为若干小块,白块仍然保持原偏振态,而斜线块则通过1/2波片将偏振旋转90°。液晶也能够用于制作PCP[33],但液晶材料多数用于基频光,且其透过率和抗损伤能力较差。偏振组束可以看成一种特殊的PCP,已经在美国国家点火装置(National Ignition Facility, NIF)等装置上广泛应用[34-35]。1993年Skupsky等[36]提出过一种完全消散斑的PCP方法,需要精确设计不同块之间的相位延迟,然而这种方法对波前畸变极敏感。事实上仅仅通过两种不同偏振态的焦斑强度叠加消除焦斑不均匀性在现实中是不可能的,这可以通过统计光学[37]说明:在波前畸变作用下,焦斑的分布必然服从随机散斑规律,其强度直方图为负指数图,平顶焦斑直方图则为狄拉克函数;而两个服从负指数分布的焦斑叠加不可能获得服从狄拉克函数的平顶焦斑。

Figure 5. (a) Polarization control plate; (b) Birefringent wedge; (c) Polarization smoothing in a convergent beam by birefringent plane
双折射楔(BW)[32]方案利用单轴晶体快慢光折射率不同的特点,通过磷酸二氢钾(Potassium Dihydrogen Phosphate, KDP)楔板直接将入射的线偏振激光分为偏振方向正交,并且具有一定角度差的两束激光,如图5(b)所示。两束激光的焦斑在焦平面上强度叠加,其形态接近,但位置存在偏移,只要保证偏移量大于激光散斑的相干长度(与衍射极限同量级),即能够达到减弱焦斑散斑的效果。
2005年Munro等[38]针对NIF,进一步提出,如果将偏振元件置于终端聚焦透镜之后的汇聚光路段,则可以通过平行晶体板获得单束偏振匀滑效果,如图5(c)所示;2015年,Huang Xiaoxia等[39]人报道了汇聚光束偏振匀滑实验效果,结果表明此方法可以安全地使用在SG-III上。
2015年,任广森等[40]分析了径向偏振调制对聚焦光斑匀滑及偏振特性的影响,结果表明,无论是径向偏振调制还是PCP,抑或是BW方案,不同PS设计本质上具有一致性,光束的匀滑及偏振特性差别较小。
-
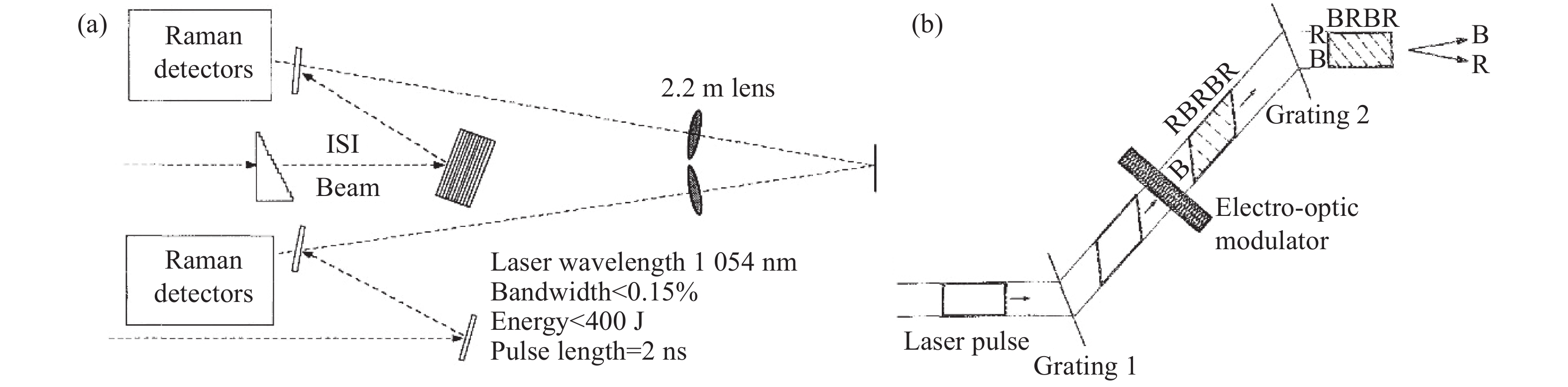
诱导空间非相干(ISI)方法由Lehmberg等[27, 41]在1983年提出。ISI需要使用在具有一定带宽的激光上,利用宽带激光具有一定相干时间的特点,在光束近场分块引入时间延迟,从而消除子光束间的相干性。这些不相干子光束的远场在焦平面不相干地叠加,从而在一定积分时间内消除散斑。ISI方法可以通过调整子束的传播方向来控制远场形态[27],这种方式虽然具有灵活性的调整能力,但其实验实现太过繁琐。更容易的方式是将ISI与LA[42]或CPP[29]联用。
ISI方法首先被用在美国的Pharos III钕玻璃激光上[43],通过使用方向垂直的两块阶梯状反射楔板来引入时间延迟,如图6(a)所示。其光束相干时间接近2 ps,阶梯高度也是2 ps。互相垂直的两组楔板将光束分割为约350束子光束。事实上Pharos III的ISI台阶高度与相干时间接近,很难保证完全消除残余干涉;另一方面,通过双阶梯板引入时间延迟使近场相干度分布具有高度周期性。这样的情况下焦斑可能会出现较弱的周期性残余干涉条纹。Pharos III上的物理实验表明ISI在小于0.15%带宽的情况下已经能够大幅度抑制SBS、SRS等LPI过程和流体力学不稳定性过程。ISI+RPP的组合也在英国的VULCAN激光上使用过[25],实验结果表明ISI+RPP能够在低ISI分割数情况下大幅度改善焦斑形态的不规则;ISI+RPP的组合能够抑制发展时间在25 ps左右成丝不稳定性,进而抑制成丝后局部强点引起的SRS和SBS。最近,ISI+LA[44]和ISI+CPP的组合被使用在上海激光等离子体研究所的“昆吾”宽带二倍频激光器上,获得了高均匀性的激光焦斑,并证明了ISI方法对SBS、SRS具有明显抑制效果。

Figure 6. (a) ISI on Pharos III by using two stair plate, time delay is seperatly induced by using vertical stair-shaped echelon; (b) Method of SSD
ISI的近场低相干是通过台阶板引入的,台阶板的硬边衍射不利于光学元件安全,同时衍射损耗也限制ISI近场不相干子束的数目无法任意增加。如果光束本身就具有空间低相干性,就能避免台阶板的使用,这就是无楔板的诱导空间非相干(Echelon Free Induced Spatial Incoherence, EF-ISI)[27]。EF-ISI中使用了具有低空间相干性的扩展光源,通过空间小孔或可变透过率元件在物面取出具有合适形态的低相干光源,再通过像传递系统,将物(小孔)以合适的放缩倍率传递至像面(靶面);传递过程中增加合适的激光放大器。法国的Phebus激光使用钕玻璃放大器对多模光纤端面发出的光进行放大[45]。然而实验发现空间低相干激光的增益能力较低,其饱和通量约为窄带光的一半,分析表明这可能由空间低相干引起的局部自聚焦强点产生的双光子吸收导致[46]。美国的NIKE使用电子束泵浦的KrF放大器放大248 nm波长激光[47],获得了1%的单束不均匀性和1~3 THz的带宽。国内建成的天光一号KrF激光器[48],也通过EF-ISI方法获得了均匀性极好的焦斑。
虽然使用EF-ISI方法的KrF激光器能获得大带宽、均匀性极好的焦斑,但KrF激光器造价较高,结构复杂,不便于大规模工程集成。而使用钕玻璃等固体增益介质的EF-ISI的放大、频率转换能力较差,使得难以获得高能量输出。因此EF-ISI目前并未在高功率激光装置上广泛使用。
-
角色散匀滑(ADSP)由Nakano等[49]于1993年提出,被使用在Gekko XII的部分相干光上。通过光栅引入角色散,使不同波长的焦斑在某方向上散开,从而在强度叠加后改善焦斑的强度均匀性。然而文中认为激光的散斑会因角色散而在一倍相干时间内多次发生重构的观点有待进一步考证。相干时间内散斑模式应当相对稳定,否则就与相干时间的定义相矛盾。角色散能够进一步改善焦斑的均匀性,但对于部分相干光的焦斑的时间特性的影响的研究并未见报道。角色散一般只能产生一维匀滑效果,如何实现二维角色散匀滑仍然有待研究。
-
谱色散匀滑(SSD)由Skupsky等[23]于1989年提出,通过光栅对和电光调制器的组合使用获得在时间和空间上具有周期频率调制的脉冲,如图6(b)所示,能够获得动态的焦斑,同时避免下游光学元件发生SBS过程。色循环数是指光束等时间面上的瞬时频率循环数目,等价于光束的空间角色散量。因为周期性调制,SSD的光谱具有离散结构。在低色循环数下,SSD焦斑在空间相应方向将随时间扫动(扫动周期等于调制周期)[50-51],从而在时间积分后降低焦斑的不均匀性。高色循环数下,SSD的焦斑由若干扫动的子焦斑相干叠加得到,在瞬时散斑上存在周期性的干涉条纹。SSD焦斑RMS的精确演化不服从公式(2)(SSD瞬时焦斑不是随机变化而是周期性变化的);因摆动长度有限,SSD焦斑残留不均匀性偏高。二维SSD[52](1995)、三向SSD[53](2002)通过增加具有不同频率和方向的时空调制,能够使焦斑发生二维的扫动。如果认为SSD光谱较密集,近似为连续谱,则SSD方法的焦斑均匀性可通过下面的公式估计:
式中:θDL=波长/近场宽度,是焦斑的衍射角;θAD、θAD,x、θAD,y是SSD或高维SSD在某方向上的色散角。
高维SSD能获得更高的焦斑均匀性,这种效果是通过使瞬时焦斑的扫动方向随时间变化实现的。但如果只关注短时特性,其间多维SSD的扫动方向变化不大,焦斑的时空演化特性则与普通SSD相同。多维SSD不同方向的调制频率具有较大的最小公倍数,因此焦斑不是完全周期性的。但其近场信息不具有多样性,意味着其焦斑演化随机性较低。多频SSD[54](Multiple-Frequency Modulation Smoothing by Spectral Dispersion, Multi-FM-SSD, 2007)串联使用了多个不同频率的电光调制器,从而随时间改变焦斑扫动速度。这些改进并没有改变SSD焦斑的根本演化特性。事实上,多维SSD的焦斑重构速度取决于调制周期,然而现有的电光调制周期一般在几十ps左右,因此焦斑形态在短时间内并无根本性变化,而只是通过移动或改变重叠方式获得动态焦斑;从焦斑所包含信息的角度来看,几十ps内焦斑所包含的信息并没有发生变化。高维SSD时间域散斑尺寸由焦斑平移速度和空间散斑尺寸决定,一般大于相应带宽下的相干时间,因此其焦斑不均匀性降低的速度较慢,激光的带宽没有完全获得利用。物理实验表明高维SSD在直接驱动过程中,主要优势在于能够降低印痕效应,而对后续的不稳定性过程的抑制能力基本等同于一维SSD[55]。相比之下高维SSD的植入代价较高,因此在NIF只使用了一维SSD。
SSD的使用中可能会出现幅频调制的现象[56],导致激光脉冲的时间波形出现周期性调制。这种现象是由激光系统的色散、增益窄化导致的,可以通过光谱滤波、色散补偿等手段改善。
2000年Holstein等[57]报道了使用聚焦光栅的纵向SSD方法(Longitudinal Smoothing by Spectral Dispersion, L-SSD),这种方法与传统SSD的区别在于,通过聚焦光栅在聚焦光束的同时引入色散,不同频率光的焦距有所不同,其光斑在靶面不相干叠加,从而减弱散斑;2019年Duluc等[58]理论上比较了LSSD和传统SSD的光场演化和SBS抑制能力,结果表明在相同的纵向散斑特征尺寸下两种方法的SBS增长率相当,但LSSD的SBS饱和强度更高,这可能因为该方案焦区存在较多的局域强点。
2011年张锐等[59]提出了使用特殊光栅的SSD方法,研究表明使用星光栅的SSD具有二维匀滑效果。然而特殊光栅的制作难度限制了这些方法的实际应用。
2014年,Emeril等[60]提出了多色组束的star-driver方案,通过使用万量级数目的多色光束,结合2D-SSD获得高均匀性的靶面辐照用于直接驱动,研究表明这种设计能够获得1%以下的辐照不均匀性[5],足够的带宽使其能够抑制直接驱动中的各种LPI过程[61-62]。
2014年,钟哲强等[63]针对NIF的四束组束方式,进一步提出了多色、多频、多向的SSD组束的匀滑方式,通过在组束的四束激光上使用不同中心频率、不同调制频率、不同色散方向的一维SSD获得更快的匀滑速度和接近2D-SSD的匀滑效果。
-
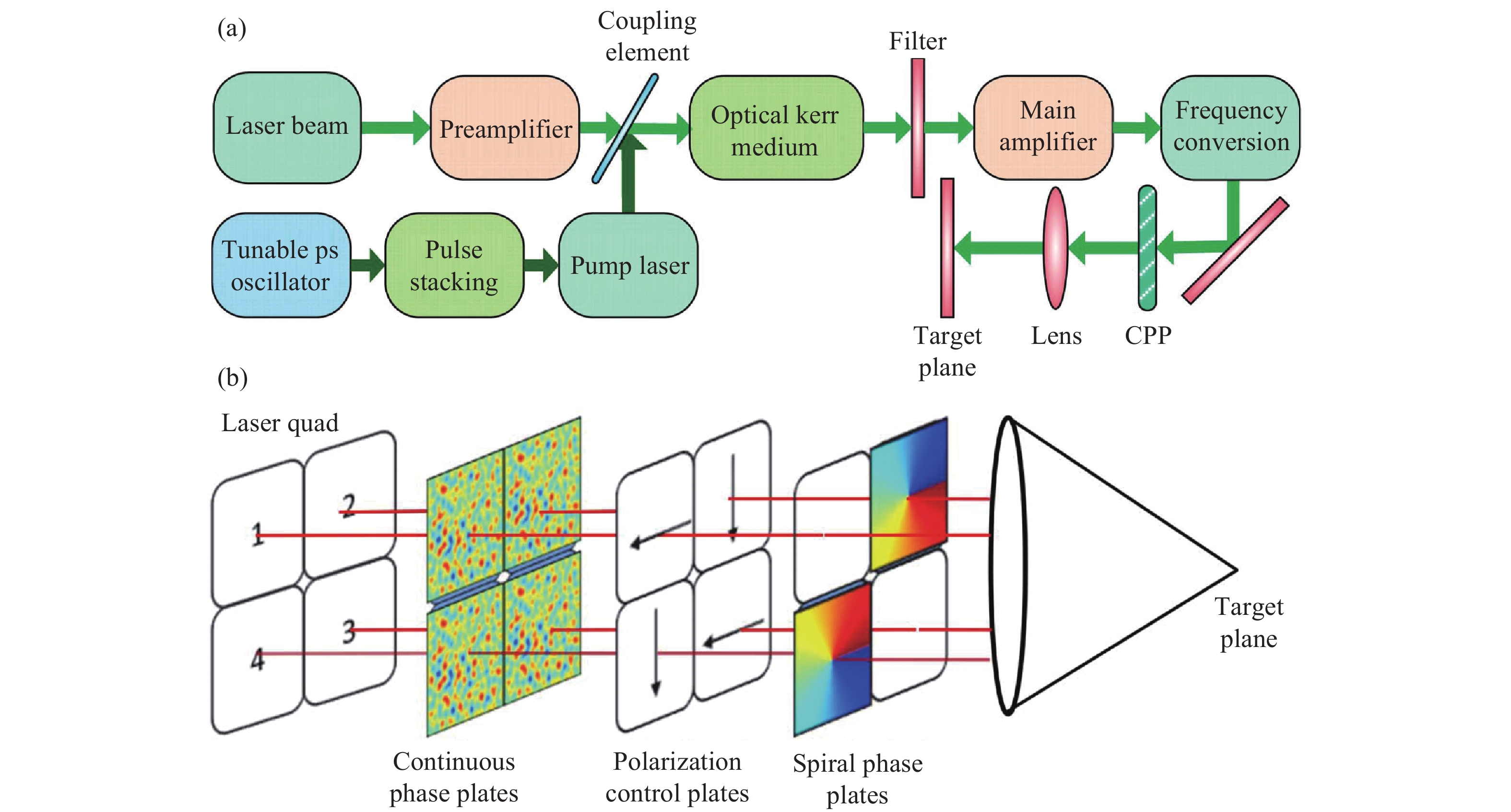
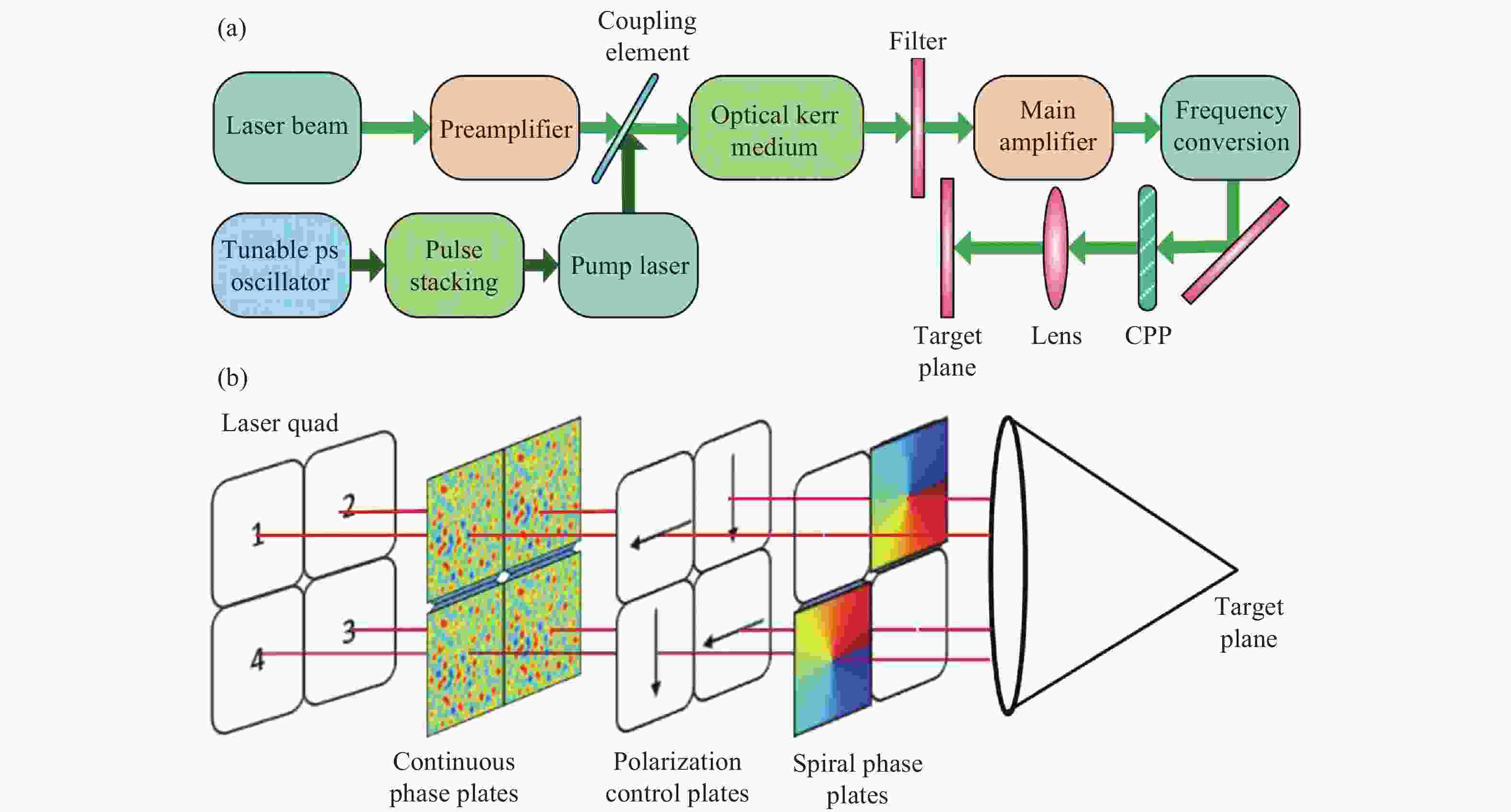
2014年,钟哲强等[64]提出了基于光克尔效应的径向匀滑(RS)方案。如图7(a)所示,使激光与高斯脉冲序列同时通过光克尔介质,利用三阶非线性效应在激光上增加随时间周期性变化的额外聚焦相位,从而使焦斑随时间发生周期性的散焦。光克尔介质的使用实际上相当于在光束近场不同半径处改变了调制幅度,而传统SSD则是在近场不同位置使用不同的调制初始相位因子。可以预期径向匀滑方案的效果将类似于LSSD,但超短脉冲的使用使得径向匀滑可以将调制周期减小到ps量级(受限于光克尔介质的相应时间),从而获得更快的匀滑速度和更大的调制带宽。然而为了产生足够的非线性折射率所需的高强度、周期性高斯脉冲序列难以物理实现,限制了这种方法的实际使用。此外近场中心处调制幅度接近于0,意味着这部分所对应的焦斑并没有得到足够的匀滑效果。
2016年,侯鹏程等[65]对RS方法进行了优化设计,指出合理安排高斯脉冲序列与主脉冲的时间关系能够最优化焦斑均匀性,而高斯脉冲序列的脉冲能量起伏会导致束匀滑效果变差。
2017年,翁小凤等[66]分析了RS方案中激光在非线性介质中小尺度自聚焦对焦斑均匀性的影响,结果表明应当控制泵浦高斯脉冲序列的光束质量和强度以及光克尔介质的厚度以避免焦斑均匀性的下降。
-
2018年,钟哲强等[67-70]提出了使用涡旋光束的具有超快匀滑速度的角向匀滑(AS)方法。AS方法通过使用螺旋相位板获得涡旋光束,通过偏振控制和双波长组束叠加获得动态焦斑,如图7(b)所示。理想情况下,AS能够获得快速旋转的点焦,其旋转周期由组束的波长差决定,实际上是一种拍频。在使用CPP的情况下,焦斑形态也会以相同周期快速变化。AS方法实际上是作为RS方法的补充被提出的,不使用CPP的情况下,RS有径向匀滑效果,AS具有角向匀滑效果。2019年YiMuyu等[71]理论上分析了AS+RS+SSD+CPP的组合方法效果,结果表明这样的组合能够在几ps内快速降低焦斑不均匀性。AS方法的意义主要在于能够获得动态旋转的点焦,在使用CPP的情况下其效果类似于多色光的不相干叠加。2020年黄媛等[72]提出了使用径向偏振光的改进AS方法,通过偏振控制元件将线偏振光转换为圆偏振光,从而进一步改善焦斑的均匀性。
-
2012年Afeyan等[73-74]报道了使用离散、非等间隔的随机脉冲序列(spike trains of uneven duration and delay pulse, STUD)打靶的束匀滑方案。按设想,STUD脉冲应当由许多短脉冲序列构成,并具有一定的占空比和强度变化;此外焦斑的空间形态也需不断随时间变化。针对这种特殊脉冲进行的理论模拟表明STUD具有占空比的特性使它能够大幅度减小SRS、SBS等LPI过程[75-76]。然而STUD脉冲的完全实现具有相当的困难,已经提出通过使用时域透镜[77]、脉冲堆积等方案获得STUD脉冲的方案。然而这些设计都只限于近场,在聚焦后的远场维持光场的高占空比特性同时保证焦斑空间匀滑是极困难的。此外,STUD的高占空比特性使它难以获得高效的放大,且对光学元件安全不利。
-
美国的国家点火装置(NIF)上使用了SSD+CPP+PS[34]的束匀滑方案。NIF透镜焦距为7.7 m,近场宽度约0.34 m,对应的散斑尺寸为λF/D=7.9 μm。除了为了抑制SBS使用的30 GHz带宽(3 GHz调制频率)外,SSD主要通过使用17 GHz的调制实现,其基频带宽为45 GHz。每组2×2组束的激光中有两束通过置于最后的半波片将偏振旋转90°,从而实现偏振匀滑。不同锥角的光束所使用的CPP规格有所不同,单束焦斑的椭圆率是0.58或0.72,焦斑长轴在1.2~1.8 mm之间。为减小CPP对三倍频效率的影响,NIF目前将CPP置于二倍频段。
美国的OMEGA激光器具有2D-SSD+CPP/DPP+PS的束匀滑能力。2004年Regan等[26]报道了带宽达到1 THz的2D-SSD,使用了基频上10.4、3.3 GHz的调制频率,14.3、6.15 rad的调制深度,0.300 ns/m和1.13 ns/m的调制倾斜参数。OMEGA焦距为180 cm,近场直径27.5 cm。其色散幅度约为72倍和38倍散斑尺度,可以预期其焦斑不均匀性约为
$ 1/\sqrt{72\times 38} $ =0.019。实验上观测到了2.7%的焦斑不均匀性(k>0.04 μm−1)。2013年报道了multi-FM-SSD在OMEGA-EP上的使用[78]。OMEGA-EP的长脉冲在时间上分为预脉冲和主脉冲。预脉冲使用了具有更大带宽的multi-FM-SSD,包含三个串联的、位于基频段的正弦调制,获得了带宽约0.5 THz的三倍频脉冲。主脉冲被调制展宽约0.1 THz,主要用于避免SBS损伤光学件。使用更大带宽的预脉冲主要为了减弱激光的印痕效应,2016年OMEGA-EP上的物理实验[79]表明,multi-FM-SSD成功将印痕效应减弱50%。 -
国内的神光二(SG-II)激光器具有SSD+LA[80]和SSD+CPP(DPP)[81-82]的束匀滑能力。SSD包含3 GHz和10 GHz的调制器,最高能得到270 GHz带宽的三倍频脉冲,其色散角达到24.9倍衍射极限。在SSD+LA中,为获得高均匀性的焦斑,LA方法需要使用软边避免焦斑中的菲涅尔衍射[83],这将导致透过率下降至80%。在SSD+DPP中,实验结果显示SSD将焦斑不均匀性从60%下降到了16%[81]。
国内的神光三(SG-III)激光器在性能升级后使用了SSD+CPP+PS的束匀滑方案[35]。SSD包含调制频率2.488 GHz、带宽0.15 nm的用于横向SBS抑制的调制模块和调制频率19.9 GHz、带宽0.3 nm的用于束匀滑的调制模块。SG-III上使用了单束的汇聚光路PS技术,通过在汇聚光路段安装双折射平板实现。
-
法国的LMJ激光器使用了LSSD+CPP的束匀滑方案[84],其最大特点在于使用了衍射聚焦光栅对三倍频光进行聚焦,并同时引入轴向色散。衍射聚焦光栅对角度敏感,容易损伤。此方案在光路最后引入色散,虽然便于传输光路、频率转换过程的设计,但对终端的调试、维护却是极不便的。
-
美国NIKE激光器是基于EF-ISI设计的KrF激光器。通过分时复用,将4 ns的脉冲拉长至120 ns、240 ns[47]分别通过电子束泵浦的KrF放大器提取能量,再通过延时元件将脉冲恢复至4 ns。NIKE的束匀滑示意图如图8所示,通过物面小孔直接获得圆形、均匀的空间低相干光源,再通过像传递将其传递至靶面。为避免增益不均匀对焦斑均匀性的影响,放大器被置于像面的傅里叶变换平面上。通过EF-ISI技术NIKE获得了不均匀性约1%的圆形焦斑,可以获得1~3 THz的带宽。实验证明NIKE激光焦斑的高均匀性和大带宽能够大幅度改善印痕效应[85]。
-
上海激光等离子体研究所最近研制成功的宽带二倍频“昆吾”激光器[86- 87]具有ISI+LA、ISI+CPP的束匀滑能力。“昆吾”激光器通过使用超辐射源[87]、光谱预补偿[88]等方法在钕玻璃放大器上获得了高增益的宽带光输出,并通过低掺氘KDP等方法实现了高效宽带频率转换[89-90],其二倍频输出带宽能够达到3.28 THz,并同时具备窄带、STUD等多种光源的输出能力。“昆吾”的光束近场具有高空间相干性和低时间相干性,能够避免空间低相干引起的增益能力不足。目前已经开展了一系列物理实验,实验结果表明低相干光的使用能够大幅度抑制SBS、SRS等过程。
一般认为ISI方法的焦斑残留不均匀性与ISI分割数目有关,对于近场分割数为M×N的ISI,其不均匀性可通过如下公式估计:
公式(4)的成立条件是ISI不同子束的焦斑形态统计上彼此无关。只使用ISI时,子束焦斑形态并不是随机的,因此焦斑不均匀性一般不符合公式(4)。ISI+CPP(RPP)方法中,CPP(RPP)使不同子束的波前分布不同,其互相干函数接近为0,此时公式(4)成立。ISI+LA方法中,所有子束具有相同的波前分布和焦斑,焦斑形态接近为子束准近场,焦斑的不均匀性主要来自于子束准近场的菲涅尔衍射,不受ISI分割数目影响。
ISI+LA焦斑中的衍射不均匀性可以通过使用软边光阑获得改善。通过软边光阑或相位光阑将子束调整为超高斯软边形态,就可以避免焦斑中的硬边衍射[91],从而获得几乎完全平整的焦斑强度分布。LA方法与其他空间方法的最大差异在于其周期性,ISI+LA的瞬时焦斑也是周期性的,虽然散斑形态会随时间快速变化,但散斑空间周期是稳定的。
ISI+CPP焦斑的不均匀性则需要通过增加ISI分割数来降低。通过CPP模拟退火优化能获得均匀性极好的焦斑,然而这种效果对波前畸变很敏感,无法实际应用。根据公式(4),增加ISI分割数可以降低焦斑不均匀性。但为了获得1%的不均匀性,需要使用1万个不相干子束,在现有规模的装置上并不现实。
理论模拟表明,尽管ISI+LA和ISI+CPP都能够获得具有高均匀性的时间积分焦斑,但这两者的空间相关性和时空演化特性有所不同。ISI+LA的焦斑空间上具有周期性的高相干点;其瞬时焦斑强度在空间上具有周期性分布;在长时间窗口下,其匀滑速度一般低于激光带宽所对应的最大匀滑速度。ISI+CPP的焦斑在时空上都具有低相干性;其焦区强度分布的时空演化完全随机,符合随机散斑规律;其匀滑速度一般是相应激光带宽下的最大值。
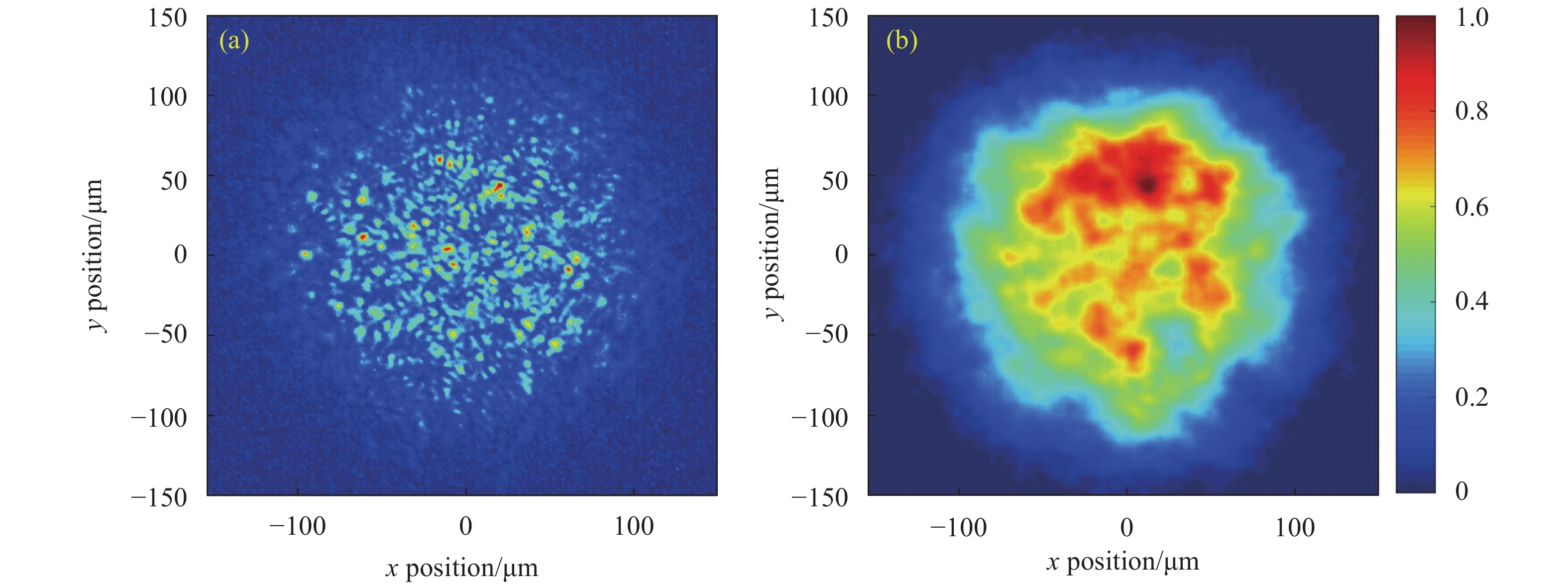
“昆吾”的ISI分割数目从3×3到8×8可选,并具有LA或CPP两种空间域匀滑能力。实测焦斑如图9所示,其中图9(a)是宽带光CPP焦斑,图9(b)是使用8×8的ISI+CPP的焦斑。ISI+CPP焦斑中心区域的RMS被降低到13%,而公式(4)的预测值为1/8=12.5%。匀滑效果主要作用在中、高频不均匀性上,仍需要对束匀滑方法进行优化以控制低频不均匀性。
-
束匀滑技术自被提出以来已经发展了40年。空间域方法中,随着光学制造和设计能力的提升,设计自由度大、衍射效率高的CPP已经成为高功率激光焦点整形的主流手段;时间域方法,则因高功率激光技术路线的发展,选择了更有利于激光器放大、频率转换过程的SSD技术成为目前的主流技术。SSD+CPP+PS的组合使单束激光的焦斑不均匀性最低降低到了2.7%。另一方面,具有连续谱的宽带激光技术路线也具有相当的潜力,EF-ISI甚至获得了1%不均匀性的激光焦斑。最近国内学者提出的RS、AS等新型束匀滑方法更让人眼前一亮。
束匀滑技术是针对不稳定过程提出的控制手段,焦区光场作为物理研究的输入条件,其精确演化特性十分重要。而目前的束匀滑技术研究多数集中在长时间积分的焦斑不均匀性控制上,对于具体的焦斑时间演化特性、焦斑相干性研究较少。与物理过程研究密切结合的束匀滑研究,往往对计算能力或实验条件要求较高,目前仍然较少。从控制印痕效应、LPI过程的角度来看,更大带宽的激光必然是高功率激光器的发展方向,相应的束匀滑技术仍有待进一步优化和发展。
Research of beam smoothing technology in high power laser driver (Invited)
doi: 10.3788/IRLA20201074
- Received Date: 2020-09-01
- Rev Recd Date: 2020-10-29
- Available Online: 2021-01-14
- Publish Date: 2020-12-24
-
Key words:
- high power laser driver /
- beam smoothing /
- induced spatial incoherence /
- smoothing by spectrum dispersion /
- polarization smoothing /
- continuous phase plate /
- lens array
Abstract: In the process of laser driven inertial confinement fusion, the inhomogeneity of light field with different spatial frequencies will cause the hydrodynamic instability, imprinting and laser plasma instability in implosion. These instabilities will eventually affect the compression ratio of implosion, thus affecting the ignition. In order to control the focal spot nonuniformity and suppress instabilities, beam smoothing technology was proposed to control the beam target coupling process through light field control. Beam smoothing can be divided into spatial smoothing and temporal smoothing. Spatial smoothing can reduce the low-frequency inhomogeneity by controlling the wavefront shape. Temporal smoothing reduces the speckle in the focal spot by controlling the coherence of the laser beam, and then reduces the medium and high frequency inhomogeneity. With the increasing demand for laser-plasmas instability suppression at higher laser power density, some new beam smoothing methods have emerged. The application of beam smoothing technology in large laser facilities was introduced, and the currently proposed beam smoothing technologies were summarized and analyzed.














 DownLoad:
DownLoad: