-
多光子吸收[1-2]是指原子或分子同时吸收两个或两个以上光子导致电子从初态跃迁到高激发态的过程。1931年,Göppert-Mayer首先提出了双光子吸收(2-photon-absorption, 2PA)[3]的概念,从理论上预测了对两个光子的同时吸收可导致电子在两个本征能级间的跃迁。激光出现后不久,Kaiser和Garrett于1961年首次报道了在GaF2:Eu2+晶体[4]中,使用脉冲红宝石激光入射而观察到由2PA诱导的频率上转换荧光发射。随着脉冲激光器的峰值功率不断提高,许多介质的三光子吸收(3PA)[5-6]、四光子吸收(4PA)[7-9],甚至更高阶的多光子吸收过程陆续被观测到。伴随着多光子吸收过程的研究,也促进了与其相关的一些新技术的出现和发展,如频率上转换激光[10]、频率上转换扫描显微成像[11]、光限幅、光稳幅[12]、三维数据储存和微加工[13]、以及深度光动力疗法[14]等。
鉴于非线性光学材料在现代光学与光电子信息领域的广泛应用,寻找高性能的非线性光学材料一直是人们普遍关注的课题,测量材料的非线性折射率和非线性吸收系数是研究材料非线性光学效应的重要内容。同时非线性光学表征技术也丰富了测量内容,拓展了测量范围。各种非线性光学表征技术已经成功应用于材料的光学非线性测量。目前,非线性光学表征技术可以分为两大类:光波混频和透射法。在光波混频方法中,非线性光学效应的产生过程由一束或多束光完成,而探测过程则由另一束光承担,如简并四波混频[15]、非线性干涉法[16]、椭圆偏振法[17]、Mach-Zehnder干涉法[18]和非线性图像法[19]等多种测量方法。在透射测量方法中,非线性光学效应的产生过程和探测过程由同一束光承担,利用单光束测量材料的非线性光学效应,如空间自相位调制(也称为自衍射)[20]、非线性透过率测量[21]和Z-扫描技术[22]。为实现多光子激励,需要一个能提供高光强水平(MW/cm2、GW/cm2或更高量级)的入射脉冲激光,这就对实验用的设备精度要求较高。另外,为了产生明显的多光子吸收效果,需要加大样品的浓度,因而也提高了实验成本。这些因素在一定程度上增加了实验上探究多光子吸收过程的难度与复杂性。
量子阻抗洛伦兹振子(QILO)[23-24]是基于Bohr-Sommerfeld量子理论和量子力学中的单、双光子吸收跃迁选择定则,通过对经典Lorentz 振子量子化而新近提出的一个微观模型,它描述了原子中的电子通过吸收光子能量(光子与电子相互作用)而发生的跃迁过程。该模型的主要特点之一是:依据介质的线性吸收光谱可以估算该介质分子的多光子吸收截面。QILO模型在描述氢原子和锂原子的单光子吸收光谱、多种有机分子的1PA和2PA光谱特性方面取得了与实验吻合较好的结果,在理论计算分子的电偶极矩、激发态寿命、以及光学晶体的倍频系数等应用中也已取得了与第一性原理的计算吻合较好的结果[23-25]。
文中在现有QILO模型的基础上,理论推导并给出了用有效量子数、电子电量及质量和玻尔半径等微观量表示的该振子四、五阶非线性效应参量的计算参考公式。数值模拟了取代基为R=NO2的含芴二茂铁衍生物的单、双及三光子吸收特性,并与实验结果进行了对比和分析。
-
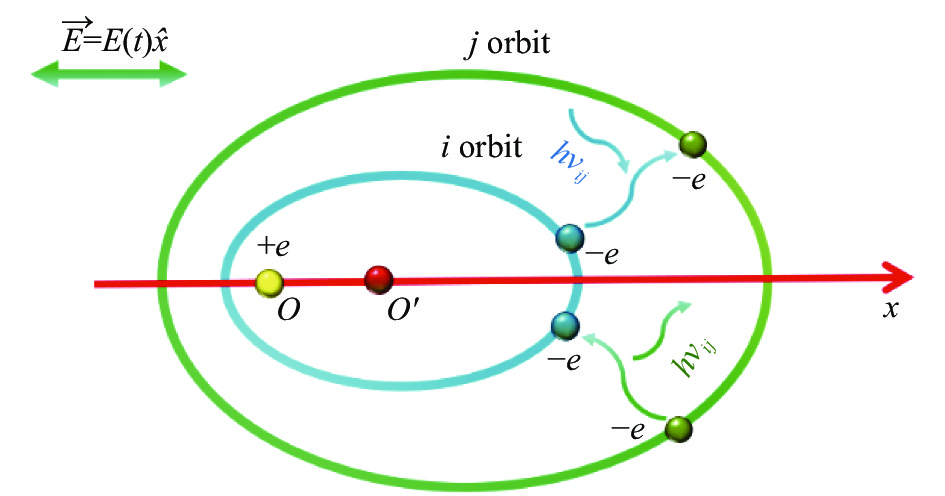
量子阻抗洛伦兹振子(QILO)描述了类氢原子中的最外层电子通过与外界进行光子能量交换而在Bohr-Sommerfeld轨道之间跃迁的光子与电子的相互作用过程,如图1所示。以原子核所在的椭圆焦点为坐标原点O,椭圆中心为$ {O}{{'}} $,则$O{O}{'}$为椭圆半焦距。电子在椭圆长轴方向相对于类氢原子核的运动可视为一个Lorentz非谐振子。

图 1 类氢原子最外层电子与光子作用的示意图
Figure 1. Interaction diagram between photon and the outermost electron of a hydrogen-like atom
类氢原子在外电场$ \mathop E\limits^ \to (t) = E(t)\mathop i\limits^ \to $的作用下从i能级跃迁到j能级的过程中,在绝热近似下,根据能量转换和守恒定律,其最外层电子沿x轴方向的运动方程在计及到五阶非线性项时可以表示为[23]:
$$ \begin{split} \frac{{{{\rm{d}}^2}x}}{{{\rm{d}}{t^2}}} +& {\varGamma _{ij}}\left(1 - i'\frac{1}{{{R_{ij}}{C_{ij}}\omega }}\right)\frac{{{\rm{d}}x}}{{{\rm{d}}t}} + \omega _j^2x - {A_j}{x^2} +\\ & {B_j}{x^3} - {C_j}{x^4} + {D_j}{x^5} = - \frac{e}{m}E \end{split}$$ (1) 式中:$ {i}{{'}}=\sqrt{-1} $;m为电子静止质量;e为电子电量;$ {C}_{ij} $为从储能等效角度以替代具有能级结构的类氢原子而引入的一个等效电容器的电容;$ {R}_{ij} $为电子从i能级跃迁到j能级的过程中所受到的电阻;$ {{\varGamma }}_{ij} $为阻尼系数,其物理意义是电子从i能级跃迁到j能级过程中受到其他原子碰撞的平均碰撞频率。其计算公式为:
$$ \begin{split} &{\varGamma _{{{ij}}}}({i_\varphi },{j_\varphi }) =\\ & \sqrt 2 \pi \left\{ {{{\left[{R_1}{j^2}\sqrt[3]{{{{\left(\frac{{{j_\varphi }}}{j}\right)}^2}}} + \delta {R'}\right]}^2} - {{\left[{R_1}{i^2}\sqrt[3]{{{{\left(\frac{{{i_\varphi }}}{i}\right)}^2}}} + \delta {R'}\right]}^2}} \right\}\overline v {N'} \end{split}$$ (2) 式中:$ \overline{v} $为电子热运动的平均速度;$ {N}{{'}} $为环境原子或分子的粒子数密度;$ {R}_{1} $为玻尔半径;$ {R}{{'}} $为与跃迁电子碰撞的环境原子或分子的有效半径;$ \delta $为一个可调参数,取决于物质的状态。气态时$ \delta =1 $,液态时$\delta \sim 0.9$(分子间的体积排斥效应)。晶体时$ \delta \sim 1.4 $(取晶格常数大约是基态原子半径的2.4倍)。jφ=j, j−1, j−2,···为有效角量子数。
Zhang等[23]通过对类氢原子的最外层电子受到的核的作用力在x轴方向的分力(QILO的回复力)的泰勒展开,在计及到三阶非线性效应的情况下,分别给出了QILO的线性及二、三阶非线性效应参数$ {\mathit{\omega }}_{\mathit{j}}^{2} $、Aj和Bj的计算参考公式。基于这些参考公式的QILO模型比较成功地描述了多种材料介质的1PA和2PA光谱特性、若干种分子的电偶极矩、激发态寿命以及一些光学晶体的倍频系数等[23-25]。鉴于三光子吸收属于五阶非线性光学效应,文中采用与文献[23]的相同方法,理论推导并得到了QILO的四、五阶非线性光学效应参数Cj和Dj的参考计算公式,以及由于计及四、五阶非线性光学效应而对原有QILO的线性及二、三阶非线性效应参数$ {\mathit{\omega }}_{\mathit{j}}^{2} $、Aj和Bj计算参考公式的影响,所得结果分列如下:
$$ \left\{ \begin{gathered} \omega _j^2 = k_j'({j_\varphi })/m = \omega _j^2({j_\varphi }) = \dfrac{{\omega _1^2({j_\varphi } = j)}}{{{j^6}}}\left\{ 1 + 3\left[1 - {\left(\frac{{{j_\varphi }}}{j}\right)^2}\right] + 6{\left[1 - {\left(\frac{{{j_\varphi }}}{j}\right)^2}\right]^2}{\text{ + 10}}{\left[1 - {\left(\frac{{{j_\varphi }}}{j}\right)^2}\right]^3}{\text{ + 15}}{\left[1 - {\left(\frac{{{j_\varphi }}}{j}\right)^2}\right]^4}\right\} \\ \omega _1^2({j_\varphi } = j) = \dfrac{{{\rm e^2}}}{{4\pi {\varepsilon _0}mR_1^3}} = 1.7 \times {10^{33}}(S I) \\ \end{gathered} \right. $$ (3) $$ \left\{ \begin{gathered} {A_j} = {A_j}\left({j_\varphi }\right) = A_j'\left({j_\varphi }\right)/m = \frac{{{A_1}}}{{{j^8}}}\left\{ 3{\left[1 - {\left(\frac{{{j_\varphi }}}{j}\right)^2}\right]^{1/2}} + 12{\left[1 - {\left(\frac{{{j_\varphi }}}{j}\right)^2}\right]^{3/2}} + 30{\left[1 - {\left(\frac{{{j_\varphi }}}{j}\right)^2}\right]^{5/2}} + 60{\left[1 - {\left(\frac{{{j_\varphi }}}{j}\right)^2}\right]^{7/2}}\right\} \\ {A_1} = \frac{{{\rm e^2}}}{{4\pi {\varepsilon _0}mR_1^4}} = 3.2 \times {10^{43}}\left(S I\right) \\ \end{gathered} \right. $$ (4) $$ \left\{ \begin{gathered} {B_j} = {B_j}\left({j_\varphi }\right) = B_j'\left({j_\varphi }\right)/m = \frac{{{B_1}}}{{{j^{10}}}}\left\{ 6\left[1 - {\left(\frac{{{j_\varphi }}}{j}\right)^2}\right] + 30{\left[1 - {\left(\frac{{{j_\varphi }}}{j}\right)^2}\right]^2}{\text{ + 9}}0{\left[1 - {\left(\frac{{{j_\varphi }}}{j}\right)^2}\right]^3}\right\} \\ {B_1} = \frac{{{\rm e^2}}}{{4\pi {\varepsilon _0}mR_1^5}} = 6.1 \times {10^{53}}\left(S I\right) \\ \end{gathered} \right. $$ (5) $$ \left\{ \begin{gathered} {C_j} = {C_j}\left({j_\varphi }\right) = C_j'\left({j_\varphi }\right)/m = \frac{{{C_1}}}{{{j^{12}}}}\left\{ 10{\left[1 - {\left(\frac{{{j_\varphi }}}{j}\right)^2}\right]^{3/2}}{\text{ }} + 60{\left[1 - {\left(\frac{{{j_\varphi }}}{j}\right)^2}\right]^{5/2}}\right\} \\ {C_1} = \frac{{{\rm e^2}}}{{4\pi {\varepsilon _0}mR_1^6}} = 1.1 \times {10^{64}}\left(S I\right) \\ \end{gathered} \right. $$ (6) $$ \left\{ \begin{gathered} {D_j} = {D_j}({j_\varphi }) = D_j'({j_\varphi })/m = \frac{{{D_1}}}{{{j^{14}}}}\{ 15{\left[1 - {\left(\frac{{{j_\varphi }}}{j}\right)^2}\right]^2}\} \\ {D_1} = \frac{{{\rm e^2}}}{{4\pi {\varepsilon _0}mR_1^7}} = 2.2 \times {10^{74}}(S I) \\ \end{gathered} \right. $$ (7) 式中:线性参数$ {\mathit{\omega }}_{\mathit{j}}^{2} $与介质的线性吸收和色散有关;二阶非线性效应参数$ {\mathit{A}}_{\mathit{j}} $与介质的和频、差频以及倍频效应有关;三阶非线性效应参数$ {\mathit{B}}_{\mathit{j}} $与材料的双光子吸收、光克尔效应以及三次谐波等特性相关;四阶非线性效应参数$ {\mathit{C}}_{\mathit{j}} $与介质材料的四次谐波产生等的四阶色散特性有关;五阶非线性效应参数$ {\mathit{D}}_{\mathit{j}} $与介质的三光子吸收、五次谐波等特性有关。
类氢原子在分子的形成中可能起着重要作用。众所周知,电子对是化学键的一种,它们被分子中两个相邻的类氢原子所共有。这两个相邻的类氢原子可以等效为具有近似相同指向的两个相互吸引的磁偶极子,通过与库仑相互作用的平衡,分子形成稳定态。在可见光附近的吸收光谱中,有许多吸收或辐射行为可以视为类氢原子的最外层电子的跃迁过程。因此,QILO是有可能适于描述许多分子或多种物质的光学特性的 [23-24]。
对公式(1)中坐标$ x\left(t\right) $和外界光电场$ E\left(t\right) $进行傅里叶变换,并根据电极化强度的定义,可以得到均匀介质的一阶电极化率的表达式:
$$ \begin{split} {\chi ^{(1)}}(\omega ) =& \sum\limits_i {\sum\limits_{j > i} {\frac{{N_{i \to j}'}}{{{\varepsilon _0}m}}} } \frac{1}{{\omega _j^2 - {\varGamma _{ij}}/({R_{ij}}{c_{ij}}) - {\omega ^2} - {i'}{\varGamma _{ij}}\omega }} = \\ & \sum\limits_i {\sum\limits_{j > i} {\frac{{N_{i \to j}'}}{{{\varepsilon _0}m}}} } {F_{ij}}(\omega ) \end{split} $$ (8) $$ {F_{ij}}(\omega ) = \frac{1}{{\omega _j^2 - {\varGamma _{ij}}/({R_{ij}}{c_{ij}}) - {\omega ^2} - {i'}{\varGamma _{ij}}\omega }} = \frac{1}{{\omega _{ij}^2 - {\omega ^2} - {i'}{\varGamma _{ij}}\omega }} $$ (9) $$ N_{i \to j}' = \frac{{g(j)}}{{g(i)}}N_{i - 1 \to i}'{{\rm{e}}^{ - ({E_j} - {E_i})/{K_B}T}} = \frac{{g(j)}}{{g(i)}}N_{i - 1}'{{\rm{e}}^{ - \hbar \omega /{K_B}T}} $$ (10) 式中:$ {N}_{i\to j}{{'}} $为在热平衡以及辐射和吸收平衡状态下从$ {E}_{i} $能级跃迁到$ {E}_{j} $能级的粒子数密度;$ g\left(i\right) $ 为$ {E}_{i} $能级的简并度。在公式(9)中,$ {\omega }_{ij} $为振子的固有角频率或电子跃迁的本征角频率,该公式表明阻尼系数$ {{\varGamma }}_{ij} $恰好表示1PA光谱的半峰全宽,与用波长表示的半峰全宽$ \Delta {\lambda }_{FWHM} $之间的关系为:
$$ {\varGamma _{ij}} = \frac{{2\pi c\Delta {\lambda _{FWHM}}}}{{\lambda _{peak}^2}} $$ (11) 式中:$ {\lambda }_{peak} $为线性吸收光谱的峰值波长; c为真空中的光速。
将一阶电极化率实、虚部分离可得:
$$\begin{split} \chi _{{\rm{Re}} }^{\left(1\right)}\left(\omega \right) =& {\sum\limits_i {\sum\limits_{j > i} {\left[\chi _{ij}^{\left(1\right)}\left(\omega \right)\right]_{{\rm{Re}} }}} } =\\ &\sum\limits_i {\sum\limits_{j > i} {\dfrac{{N_{i \to j}'{\rm e^2}}}{{{\varepsilon _0}m\omega _{ij}^2}}} } \dfrac{{1 - {{\left(\dfrac{\omega }{{{\omega _{ij}}}}\right)}^2}}}{{{{\left[1 - {{\left(\dfrac{\omega }{{{\omega _{ij}}}}\right)}^2}\right]}^2} + {{\left[\dfrac{{\omega {\varGamma _{ij}}}}{{\omega _{ij}^2}}\right]}^2}}} \end{split}$$ (12) $$ \begin{split} \chi_{{\rm{Im}} }^{\left(1\right)}\left(\omega \right) =& {\sum\limits_i {\sum\limits_{j > i} {\left[\chi _{ij}^{\left(1\right)}\right]}_{{\rm{Im}} }}} = \\ &\sum\limits_i {\sum\limits_{j > i} {\dfrac{{N_{i \to j}'{\rm e^2}}}{{{\varepsilon _0}m\omega _{ij}^2}}} } \dfrac{{\dfrac{{\omega {\varGamma _{ij}}}}{{\omega _{ij}^2}}}}{{{{\left[1 - {{\left(\dfrac{\omega }{{{\omega _{ij}}}}\right)}^2}\right]}^2} + {{\left[\dfrac{{\omega {\varGamma _{ij}}}}{{\omega _{ij}^2}}\right]}^2}}} \end{split}$$ (13) 在公式(1)的时域空间稳定解的情况下,可以得到原子跃迁的本征频率$ {\omega }_{ij} $、线性吸收光谱的峰值频率$ {\omega }_{ij}^{peak} $与阻尼系数$ {{\varGamma }}_{ij} $之间满足:
$$ \omega _{ij}^{peak} = {\omega _{ij}}\sqrt {\frac{1}{3}\left(1 - \frac{{\varGamma _{ij}^2}}{{2\omega _{ij}^2}}\right) + \frac{2}{3}\sqrt {1 - \frac{{\varGamma _{ij}^2}}{{4\omega _{ij}^2}} + \frac{1}{4}{{\left(\frac{{\varGamma _{ij}^2}}{{2\omega _{ij}^2}}\right)}^2}} } $$ (14) 在弱阻尼$ {{\varGamma }}_{ij}\ll {\omega }_{ij} $的情况下,通过泰勒级数展开,公式(14)可近似为:
$$ \omega _{ij}^{peak} = {\omega _{ij}}\left(1 - \frac{{\varGamma _{ij}^2}}{{8\omega _{ij}^2}}\right) $$ (15) 公式(14)或(15)式提供了一种根据吸收光谱的峰值频率$ {\omega }_{ij}^{peak} $和阻尼系数$ {{\varGamma }}_{ij} $来确定原子跃迁本征频率$ {\omega }_{ij} $的方法。
单光子吸收光谱一般用吸收强度和吸光度两种方式表示。根据一阶电极化率的实、虚部与折射率虚部的关系:
$$ {n_{{\rm{Im}} }} = \sqrt {\frac{1}{2}} \frac{{\chi_{{\rm{Im}} }^{(1)}}}{{\sqrt {1 + \chi _{{\rm{Re}} }^{(1)} + \sqrt {{{(1 + \chi _{{\rm{Re}} }^{(1)})}^2} + {{(\chi_{{\rm{Im}} }^{(1)})}^2}} } }} $$ (16) 线性吸收系数$ \alpha $与折射率虚部的关系为:
$$ \alpha = \frac{{4\pi }}{\lambda }{n_{{\rm{Im}} }} $$ (17) 光谱强度与吸收系数的关系为:
$$ {I_1} = {I_0}{{\rm{e}}^{ - \alpha z}} $$ (18) 式中:z为样品厚度;$ {I}_{0} $为入射强度;$ {I}_{1} $为出射强度。吸收系数$ \alpha $与吸光度A的关系为:
$$ A = \lg ({{\rm e}^{\alpha z}}) = \alpha z\lg (\rm e) $$ (19) 结合公式(16)和(17),将公式(12)和(13)代入公式(19),可以得到基于QILO模型吸光度的表达式。
在实验报道物质线性吸收光谱的众多文献中,有的文献报道了吸收光谱的吸收峰对应的半峰全宽,有的文献则没有给出吸收光谱的吸收峰对应的半峰全宽。对于在实验上没有给出半峰全宽的物质吸收光谱,则可利用基于QILO模型的吸光度的表达式,通过调节阻尼系数Γij(也即半峰全宽),在材料的线性吸收光谱的实验曲线与理论曲线拟合度达到最高的情况下,此时阻尼系数Γij的值可视为相应某一吸收峰对应的半峰全宽。
在吸收光谱的峰值频率和阻尼系数已知的情况下,利用公式(15)可以确定电子跃迁的本征频率$ {\omega }_{ij} $,再根据跃迁过程中的能量守恒:
$$ \hbar {\omega _{ij}} = {E_j} - {E_i} = \frac{{{E_1}}}{{{j^2}}} - \frac{{{E_1}}}{{{i^2}}} $$ (20) 式中:$ {E}_{1} $为氢原子的基态能量,结合阻尼系数公式(2),以及单光子吸收跃迁选择定则:
$$ \Delta l = \pm 1 $$ (21) 式中:$l=j-{j}_{\phi },{j}_{\phi }=j,j-1,j-2,\cdots$,分别对应量子力学中的s, p, d, f,···,等轨道,再考虑分子的初始极性,通过联立公式(2)、(20)、(21)求解,可以确定出吸收光谱中某一吸收峰对应的电子跃迁前后的有效量子数$ i $、$ {i}_{\phi } $、$ j $、$ {j}_{\phi } $。
与倍频相关的二阶电极化率的表达式为:
$$ {\chi }^{(2)}(\omega {,\;}\omega )=\frac{{\text{e}}^{3}}{{\varepsilon }_{0}{m}^{2}}{\displaystyle \sum _{i}{\displaystyle \sum _{j > i}(-{A}_{j})}}{N}_{i\to j}'{F}_{ij}(2\omega ){F}_{ij}^{2}(\omega ) $$ (22) 与三次谐波、双光子吸收、光克尔效应相关的三阶电极化率表达式为:
$$ \begin{split} {\chi ^{(3)}}(\omega ,\omega ,\omega ) =& \frac{{{\rm e^4}}}{{{\varepsilon _0}{m^3}}}\sum\limits_i {\sum\limits_{j > i} {N_{i \to j}'\{ 2A_j^2{F_{ij}}(2\omega ) - {B_j}\} } }\times \\ & {F_{ij}}(3\omega )F_{ij}^3(\omega ) \end{split} $$ (23) $$ \begin{split} {\chi ^{(3)}}(\omega ,\omega , - \omega ) =& \frac{{{\rm e^4}}}{{3{\varepsilon _0}{m^3}}}\sum\limits_i {\sum\limits_{j > i}} {N_{i \to j}'} {{[2A_j^2{F_{ij}}(2\omega ) + 4A_j^2{F_{ij}}(0) - 3{B_j}]} } F_{ij}^3(\omega ){F_{{{ij}}}}( - \omega ) \end{split} $$ (24) 与三光子吸收相关的五阶电极化率的表达式为:
$$ \begin{split} {\chi }^{(5)}(-\omega ,-\omega ,\omega ,\omega ,\omega )=& \dfrac{{\rm e}^{6}}{10{\varepsilon }_{0}{m}^{5}}{\displaystyle \sum _{i}{\displaystyle \sum _{j > i}{N}_{i\to j}^{\text{'}}\{4{A}_{j}^{4}[8{F}_{ij}(0){F}_{ij}(\omega ){F}_{ij}(2\omega )+2{F}_{ij}(0){F}_{ij}(-\omega ){F}_{ij}(2\omega )}}+\\ & 2{F}_{ij}(-2\omega ){F}_{ij}(-\omega ){F}_{ij}(0)+8{F}_{ij}^{2}(0){F}_{ij}(\omega )+4{F}_{ij}^{2}(0){F}_{ij}(-\omega )+{F}_{ij}(2\omega ){F}_{ij}(-2\omega ){F}_{ij}(-\omega )+\\ & 2{F}_{ij}^{2}(2\omega ){F}_{ij}(\omega )+{F}_{ij}(-2\omega ){F}_{ij}(2\omega ){F}_{ij}(3\omega )+2{F}_{ij}^{2}(2\omega ){F}_{ij}(3\omega )+{F}_{ij}(2\omega ){F}_{ij}(-2\omega ){F}_{ij}(0)+\\ & 2{F}_{ij}^{2}(2\omega ){F}_{ij}(0)+2{F}_{ij}^{3}(0)]-2{A}_{j}^{2}{B}_{j}[24{F}_{ij}(0){F}_{ij}(\omega )+12{F}_{ij}(0){F}_{ij}(-\omega )+3{F}_{ij}(-\omega ){F}_{ij}(2\omega )+\\ & 3{F}_{ij}(-\omega ){F}_{ij}(-2\omega )+12{F}_{ij}(\omega ){F}_{ij}(2\omega )+{F}_{ij}(-2\omega ){F}_{ij}(3\omega )+5{F}_{ij}(2\omega ){F}_{ij}(3\omega )+3{F}_{ij}(-2\omega ){F}_{ij}(2\omega )+\\ & 6{F}_{ij}^{2}(2\omega )+15{F}_{ij}(0){F}_{ij}(2\omega )+3{F}_{ij}(0){F}_{ij}(-2\omega )+18{F}_{ij}^{2}(0)]+3{B}_{ij}^{2}[3{F}_{ij}(-\omega )+6{F}_{ij}(\omega )+{F}_{ij}(3\omega )]+\\ & 4{A}_{j}{C}_{j}[5{F}_{ij}(2\omega )+{F}_{ij}(-2\omega )+9{F}_{ij}(0)]-10{D}_{j}\}\times {F}_{ij}^{4}(\omega ){F}_{ij}^{2}(-\omega ) \end{split} $$ (25) 对于2PA跃迁过程,分子的双光子吸收截面可以表示为:
$$ {\sigma _2} = \frac{{h\upsilon \beta }}{{{N_A}{d_0} \times {{10}^{ - 3}}}} $$ (26) 式中:$ {d}_{0} $为样品浓度,双光子吸收系数β与三阶电极化率的关系为:
$$ \beta = \frac{{2\omega }}{{{\varepsilon _0}{c^2}n_{\rm{Re}}^2}}\chi_{{\rm{Im}} }^{(3)}(\omega ,\omega , - \omega ) $$ (27) 式中:$ \chi_{{\rm{Im}} }^{(3)} $为三阶电极化率虚部,表示为:
$$ \chi_{{\rm{Im}} }^{(3)}(\omega ,\omega , - \omega ) = \sum\limits_i {\sum\limits_{j > i} {{{[\chi _{ij}^{(3)}(\omega ,\omega , - \omega )]}_{{\rm{Im}} }} = \frac{{{\rm e^4}}}{{3{\varepsilon _0}{m^3}}}\sum\limits_i {\sum\limits_{j > i} {\frac{{N_{i \to j}'}}{{\omega _{ij}^8}} \times } } } } $$ $$ \left\{ {\dfrac{{\left(\dfrac{{2{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)\left(1 - \dfrac{{{\omega ^2}}}{{\omega _{ij}^2}}\right)\left[ {\dfrac{{\dfrac{{2A_j^2}}{{\omega _{ij}^2}}\left(1 - \dfrac{{4{\omega ^2}}}{{\omega _{ij}^2}}\right)}}{{{{\left(1 - \dfrac{{4{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{2{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}}} + \dfrac{{4A_j^2}}{{\omega _{ij}^2}} - 3{B_j}} \right]}}{{{{\left[ {{{\left(1 - \dfrac{{{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]}^3}}} + \dfrac{{\dfrac{{4A_j^2}}{{\omega _{ij}^2}}\left(\dfrac{{{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)\left[ {{{\left(1 - \dfrac{{{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} - {{\left(\dfrac{{{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]}}{{\left[ {{{\left(1 - \dfrac{{4{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{2{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]{{\left[ {{{\left(1 - \dfrac{{{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]}^3}}}} \right\} $$ 对于3PA过程,分子的三光子吸收截面可以表示为:
$$ {\sigma _3} = \frac{{{{(hv)}^2}\gamma }}{{{N_A}{d_0} \times {{10}^{ - 3}}}} $$ (28) 三光子吸收系数γ与五阶电极化率的关系为:
$$ \gamma = \frac{{5\pi }}{{\varepsilon _0^2n_{{\rm{Re}} }^2{c^2}\lambda }}\chi_{{\rm{Im}} }^{(5)}( - \omega , - \omega ,\omega ,\omega ,\omega ) $$ (29) 式中:$ \chi_{{\rm{Im}} }^{(5)}( - \omega , - \omega ,\omega ,\omega ,\omega ) $为五阶电极化率虚部,表达式为:
$$ \chi_{{\rm{Im}} }^{(5)}( - \omega , - \omega ,\omega ,\omega ,\omega ) = \sum\limits_i {\sum\limits_{j > i} {{{[\chi _{ij}^{(5)}( - \omega , - \omega ,\omega ,\omega ,\omega )]}_{{\rm{Im}} }} = \frac{{{\rm e^6}}}{{10{\varepsilon _0}{m^5}}}\sum\limits_i {\sum\limits_{j > i} {\frac{{N_{i \to j}'}}{{\omega _{ij}^{12}}} \times } } } } $$ $$\left\{\left\{\left\{\dfrac{4{A}_{j}^{4}}{{\omega }_{ij}^{6}}\left\{\dfrac{12\left(1-\dfrac{{\omega }^{2}}{{\omega }_{ij}^{2}}\right)\left(1-\dfrac{4{\omega }^{2}}{{\omega }_{ij}^{2}}\right)-{\left(\dfrac{4{\varGamma }_{ij}\omega }{{\omega }_{ij}^{2}}\right)}^{2}}{\left[{\left(1-\dfrac{{\omega }^{2}}{{\omega }_{ij}^{2}}\right)}^{2}+{\left(\dfrac{{\varGamma }_{ij}\omega }{{\omega }_{ij}^{2}}\right)}^{2}\right]\left[{\left(1-\dfrac{4{\omega }^{2}}{{\omega }_{ij}^{2}}\right)}^{2}+{\left(\dfrac{2{\varGamma }_{ij}\omega }{{\omega }_{ij}^{2}}\right)}^{2}\right]}+\dfrac{3\left(1-\dfrac{{\omega }^{2}}{{\omega }_{ij}^{2}}\right){\left(1-\dfrac{4{\omega }^{2}}{{\omega }_{ij}^{2}}\right)}^{2}-12{\left(\dfrac{{\varGamma }_{ij}\omega }{{\omega }_{ij}^{2}}\right)}^{2}\left(1-\dfrac{3{\omega }^{2}}{{\omega }_{ij}^{2}}\right)}{{\left[{\left(1-\dfrac{4{\omega }^{2}}{{\omega }_{ij}^{2}}\right)}^{2}+{\left(\dfrac{2{\varGamma }_{ij}\omega }{{\omega }_{ij}^{2}}\right)}^{2}\right]}^{2}\left[{\left(1-\dfrac{{\omega }^{2}}{{\omega }_{ij}^{2}}\right)}^{2}+{\left(\dfrac{{\varGamma }_{ij}\omega }{{\omega }_{ij}^{2}}\right)}^{2}\right]}\right.\right.\right.\right. $$ $$ \left. {\dfrac{{3{{\left(1 - \dfrac{{4{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2}\left(1 - \dfrac{{9{\omega ^2}}}{{\omega _{ij}^2}}\right) - {{\left(\dfrac{{{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}\left(28 - 132\dfrac{{{\omega ^2}}}{{\omega _{ij}^2}}\right)}}{{{{\left[ {{{\left(1 - \dfrac{{4{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{2{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]}^2}\left[ {{{\left(1 - \dfrac{{9{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{3{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]}} + \dfrac{{3{{\left(1 - \dfrac{{4{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} - {{\left(\dfrac{{2{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}}}{{{{\left[ {{{\left(1 - \dfrac{{4{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{2{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]}^2}}} + \dfrac{{12\left(1 - \dfrac{{{\omega ^2}}}{{\omega _{ij}^2}}\right)}}{{\left[ {{{\left(1 - \dfrac{{{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]}} + 2} \right\}- $$ $$ \begin{split} & \dfrac{{2A_j^2{B_j}}}{{\omega _{ij}^4}}\left\{ {\dfrac{{36\left(1 - \dfrac{{{\omega ^2}}}{{\omega _{ij}^2}}\right)}}{{{{\left(1 - \dfrac{{{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}}}} \right. + \dfrac{{18\left(1 - \dfrac{{{\omega ^2}}}{{\omega _{ij}^2}}\right)\left(1 - \dfrac{{4{\omega ^2}}}{{\omega _{ij}^2}}\right) - 24{{\left(\dfrac{{{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}}}{{\left[ {{{\left(1 - \dfrac{{{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]\left[ {{{\left(1 - \dfrac{{4{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{2{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]}} + \dfrac{{18\left(1 - \dfrac{{4{\omega ^2}}}{{\omega _{ij}^2}}\right)}}{{\left[ {{{\left(1 - \dfrac{{4{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{2{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]}}+ \\ & \left.{ \dfrac{{6\left(1 - \dfrac{{4{\omega ^2}}}{{\omega _{ij}^2}}\right)\left(1 - \dfrac{{9{\omega ^2}}}{{\omega _{ij}^2}}\right) - 24{{\left(\dfrac{{{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}}}{{\left[ {{{\left(1 - \dfrac{{4{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{2{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]\left[ {{{\left(1 - \dfrac{{9{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{3{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]}} + \dfrac{{9{{\left(1 - \dfrac{{4{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} - 3{{\left(\dfrac{{2{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}}}{{{{\left[ {{{\left(1 - \dfrac{{4{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{2{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]}^2}}} + 18} \right\} + \dfrac{{3B_j^2}}{{\omega _{ij}^2}}\left\{ {\dfrac{{9\left(1 - \dfrac{{{\omega ^2}}}{{\omega _{ij}^2}}\right)}}{{\left[ {{{\left(1 - \dfrac{{{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]}}} \right. + \\ &\left. {\left. {\dfrac{{\left(1 - \dfrac{{9{\omega ^2}}}{{\omega _{ij}^2}}\right)}}{{{{\left(1 - \dfrac{{9{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{3{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}}}} \right\} + \dfrac{{4{A_j}{C_j}}}{{\omega _{ij}^2}}\left\{ {\dfrac{{6\left(1 - \dfrac{{4{\omega ^2}}}{{\omega _{ij}^2}}\right)}}{{\left[ {{{\left(1 - \dfrac{{4{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{2{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]}} + 9} \right\} - 10{D_j}} \right\}\left. { \times \dfrac{{\left(\dfrac{{2{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)\left(1 - \dfrac{{{\omega ^2}}}{{\omega _{ij}^2}}\right)}}{{{{\left[ {{{\left(1 - \dfrac{{{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]}^4}}}} \right\} + \end{split}$$ $$ \left\{\left\{\dfrac{4{A}_{j}^{4}}{{\omega }_{ij}^{6}}\left\{\dfrac{\left(\dfrac{{\varGamma }_{ij}\omega }{{\omega }_{ij}^{2}}\right)\left(20-32\dfrac{{\omega }^{2}}{{\omega }_{ij}^{2}}\right)}{\left[{\left(1-\dfrac{{\omega }^{2}}{{\omega }_{ij}^{2}}\right)}^{2}+{\left(\dfrac{{\varGamma }_{ij}\omega }{{\omega }_{ij}^{2}}\right)}^{2}\right]\left[{\left(1-\dfrac{4{\omega }^{2}}{{\omega }_{ij}^{2}}\right)}^{2}+{\left(\dfrac{2{\varGamma }_{ij}\omega }{{\omega }_{ij}^{2}}\right)}^{2}\right]}+\dfrac{\left(\dfrac{{\varGamma }_{ij}\omega }{{\omega }_{ij}^{2}}\right)\left(1-\dfrac{4{\omega }^{2}}{{\omega }_{ij}^{2}}\right)\left(9-12\dfrac{{\omega }^{2}}{{\omega }_{ij}^{2}}\right)-12{\left(\dfrac{{\varGamma }_{ij}\omega }{{\omega }_{ij}^{2}}\right)}^{3}}{{\left[{\left(1-\dfrac{4{\omega }^{2}}{{\omega }_{ij}^{2}}\right)}^{2}+{\left(\dfrac{2{\varGamma }_{ij}\omega }{{\omega }_{ij}^{2}}\right)}^{2}\right]}^{2}\left[{\left(1-\dfrac{{\omega }^{2}}{{\omega }_{ij}^{2}}\right)}^{2}+{\left(\dfrac{{\varGamma }_{ij}\omega }{{\omega }_{ij}^{2}}\right)}^{2}\right]}+\right.\right.\right. $$ $$ \left. { \dfrac{{8\left(\dfrac{{{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)\left(1 - \dfrac{{4{\omega ^2}}}{{\omega _{ij}^2}}\right)}}{{{{\left[ {{{\left(1 - \dfrac{{4{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{2{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]}^2}}} + \dfrac{{\left(\dfrac{{4{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}}{{\left[ {{{\left(1 - \dfrac{{{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]}} + \dfrac{{\left(\dfrac{{{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)\left(1 - \dfrac{{4{\omega ^2}}}{{\omega _{ij}^2}}\right)\left(17 - 108\dfrac{{{\omega ^2}}}{{\omega _{ij}^2}}\right) - 12{{\left(\dfrac{{{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^3}}}{{{{\left[ {{{\left(1 - \dfrac{{4{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{2{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]}^2}\left[ {{{\left(1 - \dfrac{{9{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{3{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]}}} \right\}- $$ $$\begin{split} & \dfrac{{2A_j^2{B_j}}}{{\omega _{ij}^4}}\left\{ {\dfrac{{\left(\dfrac{{12{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}}{{\left[ {{{\left(1 - \dfrac{{{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]}}} \right. + \dfrac{{\left(\dfrac{{24{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)\left[ {\left(1 - \dfrac{{4{\omega ^2}}}{{\omega _{ij}^2}}\right) + 1} \right]}}{{{{\left[ {{{\left(1 - \dfrac{{4{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{2{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]}^2}}} + \dfrac{{\left(\dfrac{{{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)\left(30 - 48\dfrac{{{\omega ^2}}}{{\omega _{ij}^2}}\right)}}{{\left[ {{{\left(1 - \dfrac{{{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]\left[ {{{\left(1 - \dfrac{{4{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{2{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]}} +\\ & \left.{ \dfrac{{\left(\dfrac{{{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)\left(26 - 144\dfrac{{{\omega ^2}}}{{\omega _{ij}^2}}\right)}}{{\left[ {{{\left(1 - \dfrac{{4{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{2{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]\left[ {{{\left(1 - \dfrac{{9{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{3{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]}}} \right\} + \dfrac{{3B_j^2}}{{\omega _{ij}^2}}\left\{ {\dfrac{{\left(\dfrac{{3{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}}{{\left[ {{{\left(1 - \dfrac{{{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]}} + \dfrac{{\left(\dfrac{{3{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}}{{\left[ {{{\left(1 - \dfrac{{9{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{3{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]}}} \right\}+ \\ & \left. {\left. {\left. { \dfrac{{4{A_j}{C_j}}}{{\omega _{ij}^2}} \times \dfrac{{\left(\dfrac{{8{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}}{{{{\left(1 - \dfrac{{4{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{2{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}}}} \right\} \times \dfrac{{{{\left(1 - \dfrac{{{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} - {{\left(\dfrac{{{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}}}{{{{\left[ {{{\left(1 - \dfrac{{{\omega ^2}}}{{\omega _{ij}^2}}\right)}^2} + {{\left(\dfrac{{{\varGamma _{ij}}\omega }}{{\omega _{ij}^2}}\right)}^2}} \right]}^4}}}} \right\}} \right\} \end{split} $$ 利用上述方程,文中进一步研究了含芴二茂铁一种衍生物的1PA、2PA和3PA过程,数值模拟了该分子的双光子吸收截面与三光子吸收截面,并与实验结果进行了对比,详细结果如下。
-
Zheng[26]等人设计合成了两种新型含芴的二茂铁衍生物,并采用常用光谱技术研究了这两种分子的线性和非线性光学性质。实验结果显示:这两种化合物在红外区具有较大的双光子和三光子吸收特性,并且具有良好的热稳定性。
文中利用QILO模型对分子结构如图2 (a)所示的二茂铁衍生物的1PA、2PA以及3PA的光谱特性进行了数值模拟与计算。首先对该分子的1PA光谱进行了最佳拟合,如图2(b)所示,得到了在400 nm吸收峰(对应峰值角频率${\omega }_{ij}^{peak}=4.712\;4\times {10}^{15}\;{{\text{rad}}}^{-1}$)附近的阻尼系数${{\varGamma }}_{ij}=1.177\;5\times {10}^{15}{\rm s}^{-1}$,将$ {{\varGamma }}_{ij} $和$ {\omega }_{ij}^{peak} $代入公式(15)中,可得到该化合物分子在光谱峰值附近1PA跃迁过程的本征角频率${\omega }_{ij}=4.748\;9\times {10}^{15}\;{{\text{rad}}}^{-1} ({\lambda }_{ij}=397\;{\text{nm}})$。考虑到处于基态的取代基为R=NO2的含芴二茂铁衍生物是极性分子,并根据量子力学的1PA选择定则${\Delta }l=\pm 1$,笔者认为图2中400 nm附近的1PA光谱的黑线代表了该分子的$ 2 p\to 3 s $跃迁过程。将${{\varGamma }}_{ij}=1.177\;5\times {10}^{15}{\rm s}^{-1}$、${\omega }_{ij}=4.748\;9\times {10}^{15}\;{{\text{rad}}}^{-1} \left({\lambda }_{ij}=397\;{\text{nm}}\right)$、$ {i}_{\varphi }=i-1 $、$ {j}_{\varphi }=j-1 $代入公式(2),得到电子跃迁前后的有效量子数分别为$ i=1.657\;7 $、${i}_{\varphi }= 0.657\;7$、$ j=2.732\;9 $、${j}_{\varphi }= 2.732\;9$。根据2PA选择定则${\Delta }l=0$,该化合物分子电子跃迁前后的有效量子数分别为$ i=1.657\;7 $、$ {i}_{\varphi }=0.657\;7 $、$ j=2.732\;9 $、$ {j}_{\varphi }=1.732\;9 $,对应于2PA的$ 2 p\to 3 p $的过程,对应的阻尼系数为${{\varGamma }}^{\rm 2PA}=7.141\;6\times {10}^{14}\;{{\text{rad}}}^{-1}$。采用类似2PA研究同样的方法,根据3PA选择定则$ \mathrm{\Delta }l=1 $,则电子跃迁前后的有效量子数分别为$ i=1.657\;7 $、$ {i}_{\varphi }=1.657\;7 $、$j=2.732\;9$、$ {j}_{\varphi }=1.732\;9 $,对应于3PA的$ 2 s\to 3 p $的过程,对应的阻尼系数${{\varGamma }}^{\rm 3PA}=5.248\;6\times {10}^{14}\;{{\text{rad}}}^{-1}$。在公式(2)中,氯仿溶剂分子的有效半径取为$ \delta {R}{{'}}=2.857\;1\times {10}^{-10}\;{\rm{m}} $,其与分子数密度$ {N}{{'}}=7.465\;7\times {10}^{27}\;{{\rm{m}}}^{-3} $有关,其中可调参数取0.9。根据公式(4)~(7)可以得到二阶、三阶、四阶和五阶非线性效应参数分别为$ {A}_{2.732\;9}= 2.707\;3\times {10}^{41} \left(\mathrm{S}\mathrm{I}\right) $、$ {B}_{2.732\;9}=8.815\;8\times {10}^{50}\left(\mathrm{S}\mathrm{I}\right) $、$ {C}_{2.732\;9}=1.410\;6\times {10}^{60} \left(\mathrm{S}\mathrm{I}\right) $、$ {D}_{2.732\;9}=9.026\;5\times {10}^{68}\left(\mathrm{S}\mathrm{I}\right) $。使用公式(26)和(28)可以得到该化合物分子的双光子吸收截面和三光子吸收截面分别在550~1050 nm和1100~1600 nm波长范围的变化曲线,如图2(c)、(d)所示。

图 2 基于QILO对取代基为R=NO2的含芴二茂铁衍生物的单、双及三光子吸收的数值模拟。(a)分子结构; (b)基于QILO对线性吸收光谱的拟合图;(c)基于QILO的分子2PA截面(蓝线);(d)基于QILO的分子三光子吸收截面
Figure 2. Numerical simulation of single-, two-, and three-photon absorption of R=NO2-fluorene-containing ferrocene derivative based on QILO. (a) Molecular structure; (b) Fitting diagram of linear absorption spectrum based on QILO; (c) Molecular 2PA cross section based on QILO (blue line); (d) Molecular three-photon-absorption cross section based on QILO
由图2(c)和图2(d)可以分别得到基于QILO模型在$ \lambda =793\;\mathrm{n}\mathrm{m} $处的双光子吸收截面理论值和在$ \lambda = 1\;260 \;{\rm{nm}} $和$ \lambda =1\;314\; {\rm{nm}} $处的三光子吸收截面的理论值及其实验值,分列于表1中,由表1可以看出:基于QILO模型对取代基为R=NO2的含芴二茂铁衍生物的双、三光子吸收截面的数值计算结果与实验结果符合得较好。
表 1 基于QILO模型的取代基为R=NO2的含芴二茂铁衍生物的2PA和3PA截面理论与实验结果
Table 1. Theoretical and experimental results of 2PA and 3PA cross sections of R=NO2-fluorene-containing ferrocene derivative based on QILO model
Method $\begin{array}{l}{\sigma }_{2} /\times1{0}^{-20}\;{ {\rm{cm} } }^{4}\cdot{ {\rm{GW} } }^{-1}\end{array}$ $\begin{array}{l}{\sigma }_{3}/\times1{0}^{-25}\;{ {\rm{cm} } }^{6}\cdot{ {\rm{GW} } }^{-2}\end{array}$ 793 nm 1260 nm 1314 nm Experiment 0.40 3.00 2.45 Theory 0.49 2.01 1.00 鉴于目前通常认为,在高光强作用下,介质材料的非线性光学效应并不是单独发生。对于双、三光子的过程而言, 3PA的过程中也许会存在2PA的过程。如何在高光强作用下单独分离出3PA过程而忽略2PA效应?就此类问题,文中借基于QILO模型研究的取代基为R=NO2的含芴二茂铁衍生物的2PA和3PA过程为例做一简要讨论。
图3分别给出了R=NO2的含芴二茂铁衍生物在2PA和3PA波长区域范围附近内的双、三光子吸收截面和三、五阶电极化率的虚部的变化曲线。根据三阶电极化强度的定义:

图 3 基于QILO模型的取代基为R=NO2的含芴二茂铁衍生物2PA和3PA的相互影响示意图。(a) 分子2PA的截面; (b) 三阶电极化率虚部; (c) 分子3PA的截面; (d) 五阶电极化率虚部
Figure 3. Influence between 2PA and 3PA of R=NO2-fluorene-containing ferrocene derivative based on the QILO. (a) Molecular 2PA cross-section; (b) The imaginary part of the third-order electropolarization; (c) Molecular 3PA cross-section; (d) The imaginary part of the fifth-order electropolarization
$$ {P}^{(3)}({r}) = {\displaystyle \sum _{{m,n,l}}{\varepsilon }_{0}{\chi }^{(3)}({\omega }_{m},{\omega }_{n},{\omega }_{l})}\vdots E({\omega }_{m})E({\omega }_{n})E({\omega }_{l}){{\rm{e}}}^{-i({\omega }_{m}+{\omega }_{n}+{\omega }_{l})t} $$ 假设产生双光子吸收时所用的激发光强度(脉冲激光的峰值强度)约为10 $ \;\mathrm{G}\mathrm{W}/{\mathrm{c}\mathrm{m}}^{2}=10\times {10}^{13}\;\mathrm{W}/{\mathrm{m}}^{2} $,取代基R=NO2的含芴二茂铁衍生物在793 nm附近的三阶电极化率虚部为$ 1.049\times {10}^{-22}\;{\mathrm{m}}^{2}/{\mathrm{V}}^{2} $, 在此条件下,可以估算出${{P}}^{\left(3\right)}\approx 1.918\times {10}^{-8} {{\rm{C}}}/{\mathrm{m}}^{2}$。类似地,根据五阶电极化强度的定义:
$$ \begin{split} {P}^{(5)}({r})=& {\displaystyle \sum _{{\alpha }_{1},{\alpha }_{2},\cdots ,{\alpha }_{5}}{\varepsilon }_{0}{\chi }^{(5)}({\omega }_{{\alpha }_{1}},{\omega }_{{\alpha }_{2}},\cdots ,{\omega }_{{\alpha }_{5}})}|E({\omega }_{{\alpha }_{1}})E({\omega }_{{\alpha }_{2}})\cdots\\ & E({\omega }_{{\alpha }_{5}}){{\rm{e}}}^{-i({\omega }_{{\alpha }_{1}}+{\omega }_{{\alpha }_{2}}+\cdots +{\omega }_{{\alpha }_{5}})t} \end{split} $$ 假设产生三光子吸收时所用的激发光强度约为100 $ \mathrm{G}\mathrm{W}/{\mathrm{c}\mathrm{m}}^{2}=100\times {10}^{13}\;\mathrm{W}/{\mathrm{m}}^{2} $。R=NO2含芴二茂铁衍生物在1186 nm附近的五阶电极化率虚部约为$ 4.19\times {10}^{-42}\;{\mathrm{m}}^{4}/{\mathrm{V}}^{4} $。在此条件下,可以估算出${{P}}^{\left(5\right)}\approx 1.825\times {10}^{-8}\; \rm{C}/{\mathrm{m}}^{2}$,这两个估算结果说明P(3)和P(5)的值非常接近。因此需要进一步探讨在高光强作用下单独分离出3PA过程而忽略2PA效应等问题。
从图3(b)可以看出,R=NO2含芴二茂铁衍生物在1186 nm附近的三阶电极化率的虚部约为${{\chi }}_{\mathrm{I}\mathrm{m}}^{(3)} =5.5 \times {10}^{-24}\;{\mathrm{m}}^{2}\cdot{\mathrm{V}}^{-2}$,若在此波长附近取三光子激发光的强度范围在100 $\mathrm{G}\mathrm{W}/{\mathrm{c}\mathrm{m}}^{2}(100\times {10}^{13}\; \mathrm{W}/{\mathrm{m}}^{2})$附近,则由于该物质的三阶电极化在1186 nm附近产生的三阶电极化强度$ {{P}}^{\left(3\right)}\approx 3.182\times {10}^{-8}\; \mathrm{C}/{\mathrm{m}}^{2} $,该值大于由于五阶电极化产生的五阶电极化强度的值${{P}}^{\left(5\right)} \approx 1.825\times {10}^{-8}\rm{C}/{\mathrm{m}}^{2}$。鉴于R=NO2含芴二茂铁衍生物在1186 nm附近的总的非线性极化强度是该物质三阶极化和五阶极化的叠加效果,为了单独分离出3PA过程,需要设法剔除或排除三阶极化效应的影响。从图3(b)和(d)可看出,三阶电极化率的虚部$ {{\chi }}_{\mathrm{I}\mathrm{m}}^{(3)} $在1186 nm附近的变化为一单调下降的渐近线,而五阶电极化率的虚部$ {{\chi }}_{\mathrm{I}\mathrm{m}}^{(5)} $在1186 nm附近存在三光子吸收峰,此吸收峰恰好叠加在三阶电极化的虚部渐近线上,因此这一渐近线或许可以被处理成三光子吸收的背景噪声。关于信号的背景噪声的处理方法很多,故不再在此赘述。
采用上述三阶极化的分析方法对五阶极化的影响进行类似的分析,从图3(c)和(d)可以估算出:在考虑R=NO2的含芴二茂铁衍生物在793 nm附近双光子吸收过程中,五阶电极化强度在793 nm附近的值$ {{P}}^{\left(5\right)}\approx 8.801\;6\times {10}^{-11}\mathrm{C}/{\mathrm{m}}^{2} $,该值远远小于在793 nm附近的三阶电极化强度${{P}}^{\left(3\right)}\approx 1.918\times {10}^{-8}\rm{C}/{\rm{m}}^{2}$。也就是说,对于R=NO2的含芴二茂铁衍生物而言,按照QILO模型,3PA效应对2PA过程的影响可以忽略不计。
-
综上所述:量子阻抗洛伦兹振子(QILO)模型可以较好地描述取代基R为NO2的含芴二茂铁衍生物的1PA、2PA和3PA的光谱特性。QILO模型或许能为寻找具有大的双、三光子吸收截面的材料、制备具有高性能的线性和非线性光电功能材料,提供一种可供参考的辅助理论分析方法,降低研究多光子过程的实验成本。该模型也可推广到研究其他非线性光学的过程中。
Two- and three-photon absorption of the ferrocene derivative containing fluorene based on the quantum impedance Lorentz oscillator
-
摘要: 文中基于量子阻抗洛伦兹振子(Quantum Impedance Lorentz Oscillator, QILO)模型,研究了含芴二茂铁衍生物的单、双、及三光子吸收特性。首先,理论推导并给出了用有效量子数、电子电量及质量和玻尔半径等微观量表示的该振子四、五阶非线性效应参量的计算参考公式。在此基础上,利用QILO模型,通过拟合取代基为R=NO2的含芴二茂铁衍生物分子线性吸收光谱,得到了其在400 nm峰值附近的电子跃迁前后的有效量子数,并进一步推算了该分子的双、三光子吸收截面。数值计算结果显示:该化合物分子在793 nm波长附近的双光子吸收截面为$0.49\times {10}^{-20}\;{\mathrm{c}\mathrm{m}}^{4} \cdot {\mathrm{G}\mathrm{W}}^{-1}$,在1 260 nm和1 314 nm附近的三光子吸收截面分别为$2.01 \times {10}^{-25}\;{\mathrm{c}\mathrm{m}}^{6}\cdot{\mathrm{G}\mathrm{W}}^{-2}$、$1.00\times {10}^{-25}\;{\mathrm{c}\mathrm{m}}^{6} \cdot {\mathrm{G}\mathrm{W}}^{-2}$,与实验结果均吻合较好。文中结果说明:QILO模型可以较好地描述以NO2作为取代基的含芴二茂铁衍生物的单、双、及三光子的吸收特性。根据QILO模型的“依据介质的线性吸收光谱可以估算其多光子吸收截面”的特点,该模型或许能为寻找具有大的双、三光子吸收截面的材料提供一种可供参考的理论分析方法,降低研究多光子过程的综合实验成本。Abstract:
Objective In view of the wide application of nonlinear optical materials in the field of modern optics and optoelectronic information, the search for high-performance nonlinear optical materials is a common concern. In particular, an important content of nonlinear optical effect and its application is partly to develop characterization techniques and measurements of material nonlinear coefficients. In the past few decades, many new materials have been synthesized to get larger and larger molecular multi-photon-absorption cross-section through new characterization techniques. The common methods of the nonlinear optical measurement include degenerate four-wave mixing, nonlinear transmittance, Z-scanning technique, etc. In a multi-photon-absorption experiment, many factors such as the stability of excitation pulse laser with high light intensity (MW·cm-2, GW·cm-2, or higher), high accuracy of measuring equipment, and the suitable sample would lead to the increase of the experimental cost, difficulty and complexity. So, it may be a good effort to find a predictable method to estimate two- and three-photon-absorption behaviors according to the linear absorption spectrum. As far as we know, the quantum impedance Lorentz oscillator (QILO) model just has, to some extent, the predictive ability upon the linear absorptive behavior of medium. Methods QILO model was recently established and proposed, in which the classical Lorentz oscillator had been quantized via Bohr-Sommerfeld quantum theory and 1- and 2-photon-absorption selection rules of quantum mechanics. QILO's parameters including the linear or nonlinear param, the damping coefficient, and the oscillator strength have been expressed in terms of the typical quantum physical quantity, such as effective quantum number, Bohr radius, and the ground state energy of hydrogen atom. On the basis of QILO model, the reference formulae for calculating the fourth- and fifth-order nonlinear effect parameters of the oscillator are further derived theoretically and expressed in terms of effective quantum number, electronic charge and mass, and Bohr radius. Then, the single-, two-, and three-photon-absorption properties of the ferrocene derivative containing fluorene are investigated in detail. By fitting the linear absorption spectrum of the studied material, the effective quantum number before and after the electronic transition near the linear absorption peak of 400 nm wavelength is calculated by use of QILO model. As a prediction, the molecular two- and three-photon-absorption cross-sections of the same material are numerically calculated. The prediction results are compared with the experimental data in the literature. Results and Discussions The 1-, 2-, and 3-photon-absorption properties of ferrocene derivative containing fluorene with R=NO2 substituent are investigated using QILO model. The obtained major results are indicated in the fitting diagram of the linear absorption spectrum of the molecule (Fig.2(b)), the fitting diagram of the two-photon-absorption (2PA) cross-section (Fig.2(c)), and the curve of the three-photon-absorption (3PA) cross-section with the wavelength change (Fig.2(d)). The results of the theoretical numerical curves show that the 2PA cross-section of the compound molecule near 793 nm are about $0.49\times {10}^{-20}\;{\mathrm{c}\mathrm{m}}^{4}\cdot{\mathrm{G}\mathrm{W}}^{-1}$, and the 3PA cross-sections near 1 260 nm and 1 314 nm are $2.01\times {10}^{-25}\;{\mathrm{c}\mathrm{m}}^{6}\cdot{\mathrm{G}\mathrm{W}}^{-2}$ and $1.00\times {10}^{-25}\;{\mathrm{c}\mathrm{m}}^{6}\cdot{\mathrm{G}\mathrm{W}}^{-2}$, respectively. These values are in good agreement with the experimental ones. Additionally, the 2PA and 3PA processes of ferrocene derivatives containing fluorene with R=NO2 substituent, based on QILO model, are taken as an example to discuss how to separate the 3PA process and ignore the 2PA effect under high light intensity in detail. Conclusions QILO model can describe well the single-, two-, and three-photon-absorption properties of the ferrocene derivatives containing NO2 as substituent. In the light of the QILO's characteristic that multi-photon-absorption cross-section can be estimated according to the linear absorption spectrum of the medium, QILO model may provide us a theoretical analysis method for finding the materials with large two- and three-photon-absorption cross-sections so as to reduce the comprehensive experimental cost in studying multi-photon processes. The model can also be extended to other nonlinear optical processes. The QILO model exhibits itself an advantage of its great reduction of the calculation complexity and high cost confronting the first principle in dealing with both linear and nonlinear properties of optoelectronic materials as well. -
图 2 基于QILO对取代基为R=NO2的含芴二茂铁衍生物的单、双及三光子吸收的数值模拟。(a)分子结构; (b)基于QILO对线性吸收光谱的拟合图;(c)基于QILO的分子2PA截面(蓝线);(d)基于QILO的分子三光子吸收截面
Figure 2. Numerical simulation of single-, two-, and three-photon absorption of R=NO2-fluorene-containing ferrocene derivative based on QILO. (a) Molecular structure; (b) Fitting diagram of linear absorption spectrum based on QILO; (c) Molecular 2PA cross section based on QILO (blue line); (d) Molecular three-photon-absorption cross section based on QILO
图 3 基于QILO模型的取代基为R=NO2的含芴二茂铁衍生物2PA和3PA的相互影响示意图。(a) 分子2PA的截面; (b) 三阶电极化率虚部; (c) 分子3PA的截面; (d) 五阶电极化率虚部
Figure 3. Influence between 2PA and 3PA of R=NO2-fluorene-containing ferrocene derivative based on the QILO. (a) Molecular 2PA cross-section; (b) The imaginary part of the third-order electropolarization; (c) Molecular 3PA cross-section; (d) The imaginary part of the fifth-order electropolarization
表 1 基于QILO模型的取代基为R=NO2的含芴二茂铁衍生物的2PA和3PA截面理论与实验结果
Table 1. Theoretical and experimental results of 2PA and 3PA cross sections of R=NO2-fluorene-containing ferrocene derivative based on QILO model
Method $\begin{array}{l}{\sigma }_{2} /\times1{0}^{-20}\;{ {\rm{cm} } }^{4}\cdot{ {\rm{GW} } }^{-1}\end{array}$ $\begin{array}{l}{\sigma }_{3}/\times1{0}^{-25}\;{ {\rm{cm} } }^{6}\cdot{ {\rm{GW} } }^{-2}\end{array}$ 793 nm 1260 nm 1314 nm Experiment 0.40 3.00 2.45 Theory 0.49 2.01 1.00 -
[1] Pelosi A G, Silveira-Alves E, Cocca L H Z, et al. Two-photon absorption and multiphoton excited fluorescence of acetamide-chalcone derivatives: the role of dimethylamine group on the nonlinear optical and photophysical properties [J]. Molecules, 2023, 28(4): 1572. doi: https://doi.org/10.3390/molecules28041572 [2] Xu J, Wang T, Fang Z Y, et al. Three-photon absorption platinum (II) complexes based on DNA and L-lysine recognition for photodynamic antimicrobial therapy [J]. Sensor and Actuators B-Chemical, 2023, 376(Part B): 133051. doi: https://doi.org/10.1016/j.snb.2022.133051 [3] Göppert-Mayer M. Elementary file with two quantum fissures [J]. Ann Phys-Berlin, 1931, 9(3): 273-294. [4] Kaiser W, Garrett C G B. Two-Photon Excitation in CaF2: Eu2+ [J]. Phys Rev Lett, 1961, 7(6): 229-231. doi: 10.1103/PhysRevLett.7.229 [5] Fan Y P, Ding D C, Zhao D H. Two- and three-photon absorption and excitation phosphorescence ofoligofluorene-substituted Ir(ppy)3 [J]. Chem Commun, 2015, 51(16): 3446-3449. doi: 10.1039/C4CC09573A [6] Zhang X Y, Cao S L, Huang L L, et al. Enhanced three-photon absorption and excited up-conversion fluorescence of phenanthroimidazole derivatives [J]. Dyes Pigments, 2017, 145: 110-115. doi: 10.1016/j.dyepig.2017.05.057 [7] Grudtsyn Y V, Koribut A V, Semjonov S L, et al. Four-photon absorption cross-section measurements in UV fused silica at 473 nm [J]. Opt Lett, 2019, 44(10): 2394-2397. doi: 10.1364/OL.44.002394 [8] Ren S, Ren Y, Hu S Y, et al. Four-photon absorption properties of Mn-Doped ZnSe quantum dots [J]. IEEE Photonics J, 2019, 11(2): 4500309. doi: 10.1109/JPHOT.2019.2900255 [9] Tian Jun, Weng Guoen, Wang Youyang, et al. Random lasing in ZnO nanopowders based on multiphoton absorption for ultrafast upconversion application [J]. ACS Appl Nano Mater, 2019, 2(4): 1909-1919. doi: 10.1021/acsanm.8b02300 [10] He G S, Markowicz P P, Lin T C, et al. Observation of stimulated emission by direct three-photon excitation [J]. Nature, 2002, 415(6873): 767-70. doi: 10.1038/415767a [11] Maits S, Shear J B, Williams R M, et al. Measuring serotonin distribution in live cells with three-photon excitation [J]. Science, 1997, 275(5299): 530-532. doi: 10.1126/science.275.5299.530 [12] He G S, Bhawalkar J D, Prasad P N, et al. Three-photon-absorption-induced fluorescence and optical limiting effects in an organic compound [J]. Opt Lett, 1995, 20(14): 1524-1526. doi: 10.1364/OL.20.001524 [13] Farsari M, Filippidis G, Fotakis C, et al. Fabrication of three-dimensional structures by three-photon polymerization [J]. Opt Lett, 2005, 30(23): 3180-3182. doi: 10.1364/OL.30.003180 [14] Collins H A, Khurana M, Moriyama E H, et al. Blood-vessel closure using photosensitizers engineered for two-photon excitation [J]. Nature Photonics, 2008, 2(7): 420-424. doi: 10.1038/nphoton.2008.100 [15] Friberg S, Smith P. Nonlinear optical glasses for ultrafast optical switches [J]. IEE J Quantum Elect, 1987, 23(12): 2089-2094. doi: 10.1109/JQE.1987.1073278 [16] Adair R, Chase L L, Payne S A. Nonlinear refractive index measurements of glasses and crystals [J]. AIP Conf Proc, 1987, 160(1): 124-127. doi: https://doi.org/10.1063/1.36709 [17] Owyoung A. Ellipse rotation studies in laser host materials [J]. IEE J Quantum Elect, 1973, 9(11): 1064-1069. doi: 10.1109/JQE.1973.1077417 [18] Boudebs G, Chis M, Nguyen X P. Third-order susceptibility measurement by a new Mach Zehnder interferometry technique [J]. J Opt Soc Am B, 2001, 18(5): 623-627. doi: https://doi.org/10.1364/JOSAB.18.000623 [19] Boudebs G, De Araujo C. Characterization of light-induced modification of the nonlinear refractive index using a one-laser-shot nonlinear imaging technique [J]. Appl Phys Lett, 2004, 85(17): 3740-3742. doi: 10.1063/1.1810624 [20] Durbin S D, Arakelian S M, Shen Y R. Laser-induced diffraction rings from a nematic-liquid-crystal film [J]. Opt Lett, 1981, 6(9): 411. doi: 10.1364/OL.6.000411 [21] Miah M I. Determination of multiphoton absorption coefficient of cadmium iodide using nonlinear transmittance and photoluminescence methods [J]. Opt Mater, 2001, 18(2): 231-234. doi: 10.1016/S0925-3467(01)00168-9 [22] Awalludin A, Syuhada A, Rosli M I, et al. The study of nonlinear optical properties of aqueous acid fuchsin dye and its optical power limiting using Z-Scan method [J]. Opt Mater, 2021, 112: 110540. doi: 10.1016/j.optmat.2020.110540 [23] Zhang J, Li K, Fang Z J, et al. Quantum impedance Lorentz oscillator and its 1- and 2-photon-absorption applications [J]. AIP Adv, 2021, 11(7): 075218. doi: 10.1063/5.0055077 [24] Bai Q Q, Fang Z J, Wang X F, et al. Charge transfer and level lifetime in molecular photon-absorption upon the quantum impedance Lorentz oscillator [J]. ACS Omega, 2023, 8(22): 19950-19962. doi: 10.1021/acsomega.3c01922 [25] 白琦琪, 李凯, 王晓凤, 等. 基于量子阻抗Lorentz振子的三种晶体二次谐波特性[J]. 激光与光电子学进展, 2023, 60(21). Bai Qiqi, Li Kai, Wang Xiaofeng, et al. The second harmonic characteristics of the three crystals based on the quantum impedance Lorentz oscillator[EB/OL]. (2022-11-21)[2023-07-05]. https://kns.cnki.net/kcms/detail/31.1690.TN.20221121.0939.008.html. (in Chinese) [26] Zheng Q, He G S, Lu C, et al. Synthesis, two-and three-photon absorption, and optical limiting properties of fluorene-containing ferrocene derivatives [J]. J Mater Chem A, 2005, 15(34): 3488-3493. doi: 10.1039/b508005c -






 下载:
下载: