下载:
-
光学大气数据测量技术指利用大气气溶胶粒子散射和激光多普勒测速原理，实现飞行器真空速、攻角、侧滑角等大气参数的精确测量，具有测量范围大、精度高、不受飞行器气流影响、安装方便、维护成本低、隐身性好等优点，可解决传统大气机应用的痛点问题，如测量受气流影响、误差大、低速测量不敏感、大机动测量超范围、空速管易结冰或异物堵塞、响应慢、校准及维护复杂等，是新一代大气数据系统的首选方案。直升机对高精度、大动态范围的大气数据测量需求较为迫切，表现为直升机起降、悬停、低空或贴地飞行、倒飞时空速较低，传统大气机测量不敏感或误差大，使得低速下空速、风速及风向测量不准确，影响直升机飞行性能。目前国外多家机构已推出工程样机并完成试飞，如美国OADS公司、国家大气研究中心、Ophir公司、密歇根航宇公司、法国ONERA等，预计2022年将装备应用[1-6]。
真空速、攻角、侧滑角反演作为大气数据解算的最后一步，其反演精度决定最终的大气数据精度，对其分析有助于指导及优化系统设计。通过合理设置方位角，可以简化三波束及四波束测量的反演方程，从而获得真空速反演精度的解析解。因此，针对三波束及四波束测量的真空速反演精度多有报道[7-9]。但随着激光束数目增加，反演方程变为超定方程，难以获得真空速的解析解。因而针对多波束测量，其三轴真空速、攻角及侧滑角的反演精度分析未见报道。文中通过分析误差传递规律，得出三轴真空速反演精度与系数矩阵的关系式，仿真分析了多波束测量时三轴真空速的反演精度，并在此基础上分析了攻角及侧滑角的反演精度。
-
光学大气数据测量的一般流程：系统向大气中发射多束彼此独立的激光束，用于测量激光视线方向飞行器与气溶胶粒子的相对速度（简称视线速度），多个独立的视线速度通过坐标反演可获得飞行器三轴真空速，通过三轴真空速可解算出攻角及侧滑角。
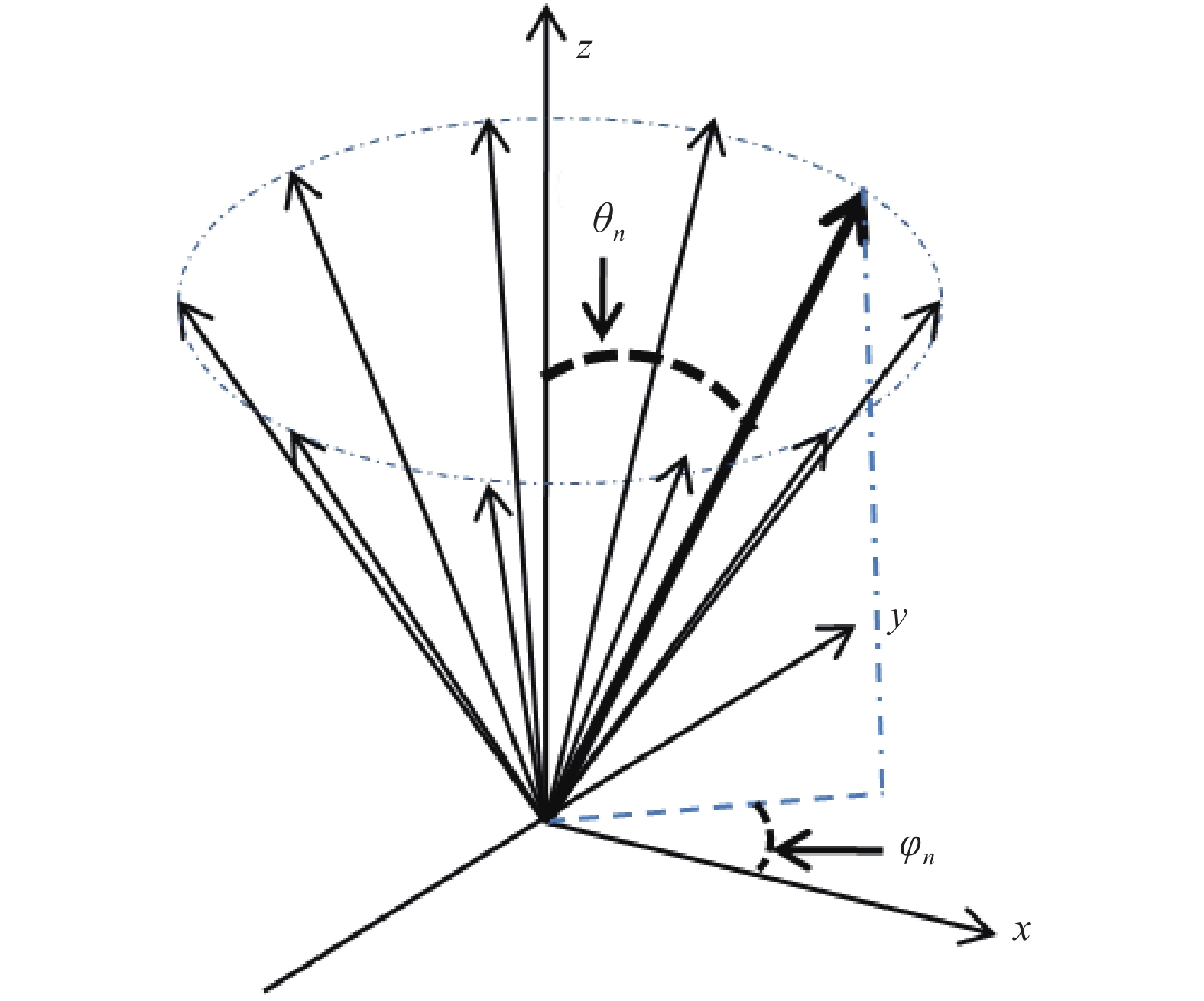
建立机体坐标系，x为机体横截面法线方向，y为机翼方向，z为机头方向，假设系统光学天线坐标与机体坐标重合（实际中可通过测量安装角度及坐标变化使其重合），则可定义激光束与z轴夹角为仰角θ，激光束在x-y平面上投影与x轴夹角定义为方位角φ，如图1所示。视线速度为三轴真空速在视线方向上的投影，因此视线速度V可表示为：
图 1 多波束测量空速反演坐标系
Figure 1. Inversion coordinate system with multi-laser beam for airspeed measurement
$$V = \left[ {\sin \theta \;\;\cos \varphi \mathop {}\nolimits^{} \;\;\sin \theta \;\;\sin \varphi \mathop {}\nolimits^{} \;\;\cos \theta } \right]\left[ \begin{gathered} {V_x} \\ {V_y} \\ {V_{\textit{z}}} \\ \end{gathered} \right]$$ (1) 式中：Vx、Vy、Vz为三轴真空速。为了获得三轴真空速，需要测量至少三个独立不相关的视线速度V，因此需要至少分别向三个独立方向上发射激光，通过坐标反演算法解算出三轴空速。
N波束激光测量，其视线速度与三轴真空速的关系可表示为：
$$\left[ \begin{gathered} {V_1} \\ {V_2} \\ \vdots \\ {V_N} \\ \end{gathered} \right] = \left[ \begin{gathered} \sin {\theta _1}\cos {\varphi _1}\mathop {}\nolimits^{} \sin {\theta _1}\sin {\varphi _1}\mathop {}\nolimits^{} \cos {\theta _1} \\ \sin {\theta _2}\cos {\varphi _2}\mathop {}\nolimits^{} \sin {\theta _2}\sin {\varphi _2}\mathop {}\nolimits^{} \cos {\theta _2} \\ \quad \vdots \quad \quad {\quad ^{}}\,\, \vdots \quad \quad \quad \vdots \\ \sin {\theta _N}\cos {\varphi _N}\mathop {}\nolimits^{} \sin {\theta _N}\sin {\varphi _N}\mathop {}\nolimits^{} \cos {\theta _N} \\ \end{gathered} \right]\left[ \begin{gathered} {V_x} \\ {V_y} \\ {V_{\textit{z}}} \\ \end{gathered} \right] = M\left[ \begin{gathered} {V_x} \\ {V_y} \\ {V_{\textit{z}}} \\ \end{gathered} \right]$$ (2) 反演出三轴真空速后，可由公式（3）解算出真空速
${V_{TAS}}$ 、攻角α、侧滑角β[3，10]：$$\left\{ \begin{gathered} {V_{TAS}} = \sqrt {V_x^2 + V_y^2 + V_z^2} \\ \alpha = \arctan \frac{{{V_x}}}{{{V_{\textit{z}}}}} \\ \beta = \arcsin \frac{{{V_y}}}{{{V_{TAS}}}} \\ \end{gathered} \right.$$ (3) 由公式（2）、（3）可知，三轴真空速、攻角及侧滑角反演精度取决于各视线速度的测量精度σ、θ及φ的角度选择。理论上，可计算任意空间分布的N束激光反演结果和精度。对于三波束及四波束测量，参考文献[7-8]给出了三轴反演风速（与三轴空速测量原理及方法相同）及反演精度的解析表达式。其中做以下假设：(1）各视线方向与z轴夹角θ相同；(2）各视线速度测量精度σ相同（决定于系统设计，可认为各束激光的光路、电路和信号解算一样）；(3）
${\varphi _n} = \dfrac{{2\pi (n - 1)}}{N}$ ，N为激光总数目，n为激光束序号。但对于N束激光测量时（N>4），由于矩阵M为N×3矩阵，公式（2）为超定方程组，无法给出解析解，此时可通过求解方程的最小二乘解反演三轴真空速，表示为：$$\left[ \begin{gathered} {V_x} \\ {V_y} \\ {V_{\textit{z}}} \\ \end{gathered} \right] = {({M^{\rm{T}}}M)^{ - 1}}{M^{\rm{T}}}\left[ \begin{gathered} {V_1} \\ {V_2} \\ \vdots \\ {V_N} \\ \end{gathered} \right] = \left[ \begin{gathered} {m_{11}}\;{m_{12}} \cdots {m_{1N}} \\ {m_{21}}\;{m_{22}} \cdots {m_{2N}} \\ {m_{31}}\;{m_{32}} \cdots {m_{3N}} \\ \end{gathered} \right]\left[ \begin{gathered} {V_1} \\ {V_2} \\ \vdots \\ {V_N} \\ \end{gathered} \right]$$ (4) 式中：
${({M^\rm T}M)^{ - 1}}{M^\rm T}$ 为3×N矩阵。由于公式（4）为线性方程，三轴真空速可表示为V1、V2、···VN的线性组合。根据线性无关变量的方差传递性质，三轴真空速的反演精度只决定于系数矩阵${({M^\rm T}M)^{ - 1}}{M^\rm T}$ ，可表示为公式（5），其中i代表x、y、z。$${\sigma _i} = \sqrt {m_{i1}^2 + m_{i2}^2 + \cdots + m_{iN}^2} \cdot \sigma $$ (5) 对公式（3）两端求微分，可推导出攻角及侧滑角反演精度表达式：
$${\sigma _\alpha } = \frac{1}{{1 + \tan {{(\alpha )}^2}}} \cdot \sqrt {{{\left( {\frac{{{\sigma _x}}}{{{V_{\textit{z}}}}}} \right)}^2} + {{\left( {\frac{{{\sigma _{\textit{z}}} \cdot {V_x}}}{{{V_{\textit{z}}}^2}}} \right)}^2}} $$ (6) $${\sigma _\beta } = \frac{1}{{\cos (\beta )}} \cdot \sqrt {{{\left( {\frac{{{\sigma _y}}}{{{V_{TAS}}}}} \right)}^2} + {{\left( {\frac{{{\sigma _V} \cdot {V_y}}}{{{V_{TAS}}^2}}} \right)}^2}} $$ (7) 式中：
${\sigma _V} = \dfrac{1}{{{V_{TAS}}}} \cdot \sqrt {{V_x}^2 \cdot {\sigma _x}^2 + {V_y}^2 \cdot {\sigma _y}^2 + {V_{\textit{z}}}^2 \cdot {\sigma _{\textit{z}}}^2}$ 。 -
三轴真空速的反演精度取决于各视线速度的测量精度σ、仰角θ及方位角φ。假设各视线速度测量精度σ相同，则可以仿真分析θ及φ对反演精度的影响。
图2为三轴真空速反演精度随仰角θ的变化情况。其中假设激光束数目N=3，各视线速度测量精度相同为σ，图中σx、σy随θ角增大误差逐渐降低，与σz具有相反的变化趋势，为保证三轴真空速反演精度小于2倍的测量精度，即σx、σy、σz均小于2σ，仰角θ取值应大于20°，小于70°。仰角θ大小的调节可通过对光学大气数据系统的光学镜头设计和装调完成，调节激光束指向与z轴的夹角即可改变仰角。直升机应用时还应综合考虑系统安装位置、系统相对机体坐标的安装角度、对三轴真空速反演精度要求等因素确定仰角大小。
图 2 空速精度随θ角变化曲线
Figure 2. Airspeed accuracy vs angle θ
图3为三轴真空速反演精度随激光束总数目N （与方位角φ相关）的变化情况。从图中可以明显看出，随着激光束数目N的增加，反演精度逐渐提高。图中z方向精度优于x、y方向是由于θ取值较小。
图 3 空速精度随激光束数目N变化关系
Figure 3. Airspeed accuracy vs laser beam number N
-
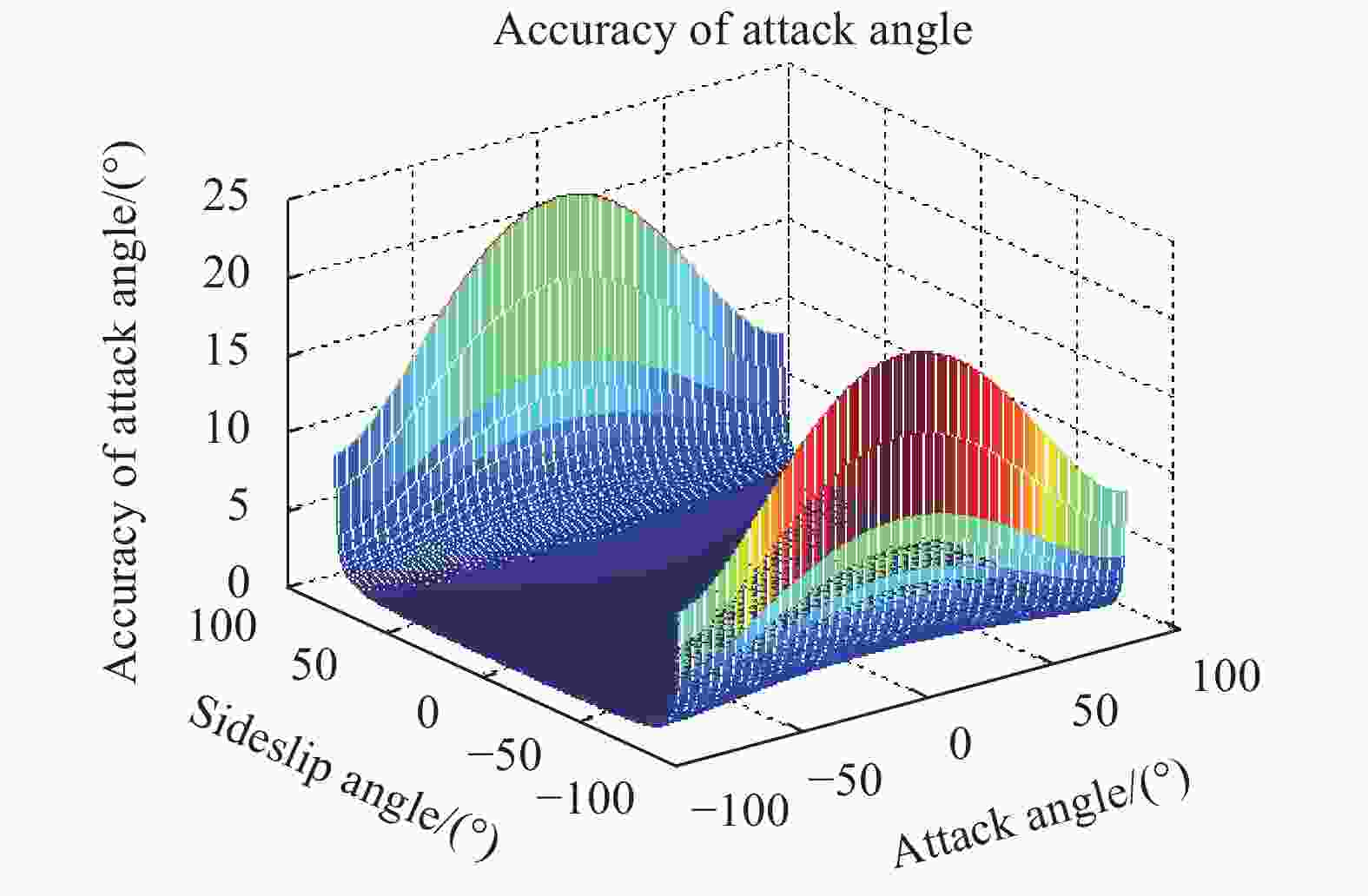
根据以上分析，理论上已知视线速度测量精度σ、仰角θ及方位角φ，便可由公式（5）~（7）分析不同飞行状态下攻角及侧滑角反演精度。假设各视线速度精度相同且σ=0.2 m/s，激光束数目N=3，图4和图5给出真空速为50 m/s时，仿真计算飞行器各姿态下攻角及侧滑角的反演精度。
图 4 各飞行状态下攻角精度（VTAS=50 m/s）
Figure 4. AOA accuracy under different flight status （VTAS=50 m/s）
图 5 各飞行状态下侧滑角精度（VTAS=50 m/s）
Figure 5. AOS accuracy under different flight status （VTAS=50 m/s）
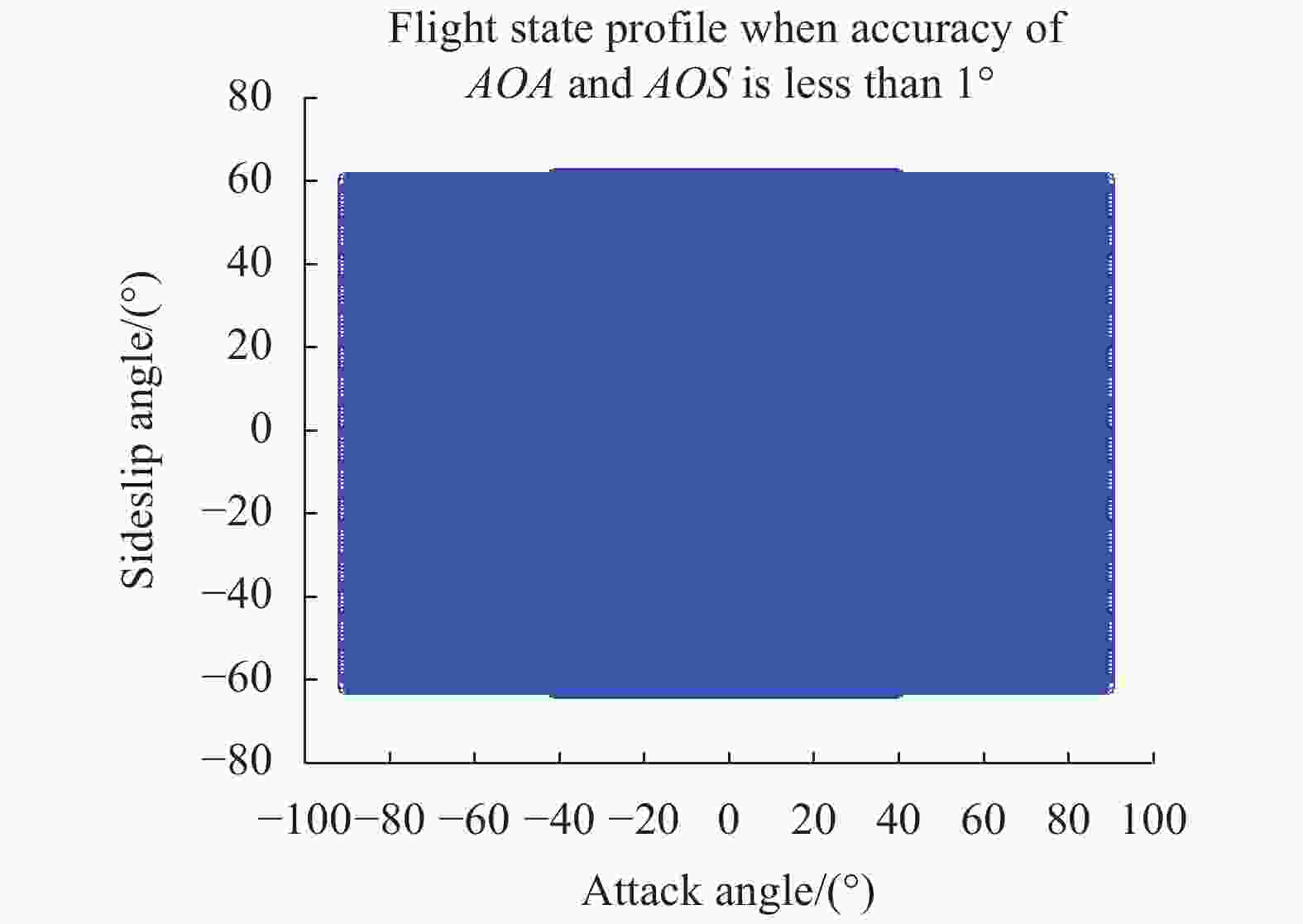
若限定反演精度，还可计算出满足特定反演精度的飞行状态范围（特指不同攻角及侧滑角组成的集合）。图6为攻角及侧滑角反演精度同时小于1°的飞行状态，攻角范围−89°~89°，侧滑角范围约−61°~61°。图7为反演精度小于3°的飞行状态，攻角范围−89°~89°，侧滑角范围约−81°~81°。
图 6 反演精度小于1°的飞行状态范围
Figure 6. Flight status range with inversion accuracy less than 1°
图 7 反演精度小于3°的飞行状态范围
Figure 7. Flight status range with inversion accuracy less than 3°
图8为给定攻角及侧滑角（AOA=AOS=30°），攻角及侧滑角反演精度随真空速的变化曲线，从图中可以明显看出，攻角及侧滑角反演精度均随真空速的增加而提高。图9为限定反演精度为1°，攻角及侧滑角最大值随真空速的变化曲线。可以看出，对于特定反演精度，攻角范围在任何空速下均为最大范围（为避免
$\tan \alpha = \infty$ ，仿真时设置的最大攻角范围为−89°~89°），意味着角度反演精度与攻角取值无关，而侧滑角取值范围随真空速的增大而增大。
图 8 角度反演精度随真空速的变化
Figure 8. Change of angle inversion accuracy with TAS
图 9 给定反演精度下角度范围随空速的变化
Figure 9. Change of angle range with TAS for a given inversion accuracy
-
为了验证上述理论及仿真分析结果，利用已搭建的激光大气数据测量原理样机(以下称样机，如图10所示)进行实验，实验方法如下。
图 10 实验用原理样机
Figure 10. Diagram of experimental setup
步骤1：用一个经校准的高精度旋转圆盘的转动线速度模拟空速，任意设定转速，使用样机测量圆盘线速度，计算激光视线速度测量精度σ；
步骤2：假定一矢量空速VTAS、攻角α、侧滑角β，可由公式（3）计算出理想三轴真空速Vxi、Vyi、Vzi，给定激光束数目N和仰角θ，计算各视线方位角
${\varphi _{{n}}}$ ，并利用公式（2）将其分解到各个激光视线方向，得到理想的激光视线速度V1i、V2i、···VNi (不同的N、θ对应不同的视线速度)；步骤3：调节旋转圆盘转速依次模拟视线速度V1i、V2i、···VNi ，将样机激光光束聚焦到旋转圆盘上，依次测量视线速度V1、V2、···VN （各采集一组数）；
步骤4：利用公式（4）将测量得到的视线速度V1、V2、···VN 反演得到三轴真空速Vx、Vy、Vz，并计算其标准差，即可得到特定N及θ的真空速反演精度；
步骤5：利用反演得到三轴真空速Vx、Vy、Vz计算攻角αm和侧滑角βm，并求其标准差，即可得到给定空速VTAS、攻角α和侧滑角β下的攻角和侧滑角反演精度。
实际测量样机的视线速度测量精度为0.037 m/s，并进行了以下三个实验。
（1）假定VTAS=10 m/s、α=β=20°、N=3，当仰角θ分别取10°、20°、30°、40°、50°、60°、70°，测量了对应的视线速度，并反演得到三轴真空速，计算其标准差得到三轴真空速的测量精度，如图11所示。可以看出，x、y轴真空速精度随θ角增大而提高，而z轴真空速精度随θ角增大而降低，测量精度与仿真精度吻合度较好。
图 11 三轴真空速精度随θ角变化曲线
Figure 11. Three-axis TAS accuracy curve with θ
（2）假定VTAS=10 m/s、α=β=20°、θ=30°，当N=3~8时，测量了对应的视线速度，并反演得到三轴真空速，计算其标准差得到三轴真空速的测量精度，如图12所示。可以看出，三轴真空速精度随激光束数目N增加而提高，实测精度与仿真精度吻合度较高。
图 12 三轴真空速精度随激光数N变化曲线
Figure 12. Three-axis TAS accuracy curve with laser beam number N
（3）假定α=β=20°、θ=30°、N=3，当VTAS分别为5、10、15、20、25、30 m/s时，测量了对应的视线速度，并反演得到攻角及侧滑角，计算其标准差得到攻角及侧滑角的测量精度，如图13所示。可以看出，攻角及侧滑角测量精度随真空速的增大而提高，实测精度与仿真精度基本吻合。
图 13 攻角及侧滑角精度随真空速变化曲线
Figure 13. The accuracy curve of AOA and AOS with TAS
-
文中通过分析误差传递模型，对多波束测量的三轴真空速、攻角及侧滑角反演精度进行了分析，并与实验结果进行了对比，仿真分析与实验结果吻合得较好。结果表明，三轴真空速反演精度随激光数目增加而提高，角度反演精度随真空速增大而提高，与攻角取值无关，给定反演精度下，侧滑角的取值范围随空速的增大而增大。文中的分析结论有助于光学大气数据测量系统的优化设计。
Analysis of data inversion accuracy of airborne optical air data system
-
摘要: 通过分析误差传递规律，仿真分析了多波束激光反演三轴真空速、攻角及侧滑角的精度变化规律，并对反演精度变化规律进行了实验验证，实验与仿真结果吻合得较好。结果表明：三轴真空速反演精度随测量激光数目的增加而提高；x、y轴与z轴真空速精度随仰角变化具有不同的趋势，为保证三轴真空速反演精度小于2倍的测量精度，仰角取值范围应在20°~70°；角度反演精度与真空速、侧滑角的取值相关，与攻角取值无关，并随着真空速增大而提高；给定反演精度下，侧滑角的取值范围随着空速的增大而增大。文中的分析结论有助于光学大气数据测量系统的优化设计。Abstract: The inversion accuracy of three-axis true air speed (TAS), angle of attack (AOA), angle of sideslipe (AOS) was analyzed by analyzing the error transmission rules of multi-beam laser measurement. In addition, experiments were carried out to verify the law of inversion accuracy change, and the experimental and simulation results were well consistent. The results show that the inversion accuracy of three-axis TAS are higher when the number of laser beams increase. The inversion accuracy of TAS in the x, y and z directions has different trends with the elevation angle. In order to ensure the three-axis TAS inversion accuracy less than 2 times the measurement accuracy, the elevation angle should be within the range of 20°-70°. The inversion accuracy of angle is related to the values of TAS and AOS rather than AOA, and it become higher as TAS increase. the range of AOS become larger as TAS increase when the inversion accuracy is given. The conclusions of this paper are useful for the optimal design of optical air data system (OADS).
-
Key words:
- OADS /
- atmospheric data /
- data invertion method /
- inversion accuracy /
- precision analysis
-
图 1 多波束测量空速反演坐标系
Figure 1. Inversion coordinate system with multi-laser beam for airspeed measurement
图 4 各飞行状态下攻角精度（VTAS=50 m/s）
Figure 4. AOA accuracy under different flight status （VTAS=50 m/s）
图 5 各飞行状态下侧滑角精度（VTAS=50 m/s）
Figure 5. AOS accuracy under different flight status （VTAS=50 m/s）
图 6 反演精度小于1°的飞行状态范围
Figure 6. Flight status range with inversion accuracy less than 1°
图 7 反演精度小于3°的飞行状态范围
Figure 7. Flight status range with inversion accuracy less than 3°
图 9 给定反演精度下角度范围随空速的变化
Figure 9. Change of angle range with TAS for a given inversion accuracy
图 12 三轴真空速精度随激光数N变化曲线
Figure 12. Three-axis TAS accuracy curve with laser beam number N
-
[1] Xiong L, Liu Y M, Huang Q P. Research progress in air data sensor technology for attack helicopter [J]. Transducer and Microsystem Technologies, 2015, 34(2): 5-8. (in Chinese) [2] Smart A E. Optical velocity sensor for air data applications[C]//Proceedings of SPIE - The International Society for Optical Engineering, 1991, 31(1): 166-173. [3] Mocker H W, Wagener T J. Laser Doppler optical air-data system: feasibility demonstration and systems specifications [J]. Appl Opt, 1994, 33(27): 6457-6471. doi: 10.1364/AO.33.006457 [4] McGann R L. Flight test results from a low-power Doppler optical air data sensor[C]//Proceedings of SPIE - The International Society for Optical Engineering, 1995, 2464: 116-124. [5] Spuler S M, Richter D, Spowart M P. Optical fiber-based laser remote sensor for airborne measurement of wind velocity and turbulence [J]. Appl Opt, 2011, 50(6): 842-851. doi: 10.1364/AO.50.000842 [6] Mamidipudi P, Dakin E A, Dakin D C. LandSafe precision flight instrumentation system: the DVE solution[C]//Proceedings of SPIE - The International Society for Optical Engineering, 2012, 8360: 83600N. [7] Pan Jingyan, Wu Shuangyang, Liu Guo, et al. Wind measurement techniques of coherent wind lidar [J]. Infrared and Laser Engineering, 2013, 42(7): 1720-1724. (in Chinese) [8] Li Ce, Zhao Pei’e, Peng Tao, et al. Technical research of 3-D wind lidar [J]. Laser Technology, 2017, 41(5): 703-707. (in Chinese) [9] 丘祖京. 相干激光雷达风场测量及数据反演方法[D]. 南京信息工程大学, 2016. Qiu Zujing. Studies on wind field measurement and data inversion method of the coherent LIDAR[D]. Nanjing: Nanjing University of Information Science and Technology, 2016. (in Chinese) [10] Long Yanzhi, Liang Yingjian, Huang Qiapping, et al. Design of optical airspeed measurement system based on Doppler shift [J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44C(12): 2521-2527. (in Chinese) -
点击查看大图
计量
- 文章访问数: 160
- HTML全文浏览量: 63
- PDF下载量: 22
- 被引次数: 0
