-
激光二极管泵浦的全固态激光器以其结构紧凑、坚固稳定以及长寿命、高效率等特点在机械加工、医疗、光信息存储以及科学研究等诸多领域都有着广泛的应用[1]。在侧面泵浦的全固态激光器中,采用旁掠射反弹结构(grazing-incidence bounce geometry)发展起来的陶瓷激光器以其输出功率高、结构稳定以及可获得接近衍射极限的输出光束质量,倍受人们关注[2]。
随着激光陶瓷材料制备工艺的不断改进,陶瓷材料与单晶材料相比,具有可大规模生产和高浓度掺杂等优点,成为当前激光系统主要的增益介质之一,已经可以替代激光晶体用于激光系统中[3]。在脉冲LD巴条泵浦激光介质的过程中,泵浦光的周期性变化引起激光介质瞬态热效应问题严重地影响了激光器输出脉冲的峰值功率以及光束质量[4-6]。
文中通过对脉冲激光二极管巴条侧面泵浦掺钕YAG陶瓷工作特点的分析,构建契合实际的热分析模型,利用Possion方程求解得出泵浦时段与泵浦间期两过程中激光陶瓷温度场与热形变场分布,定量地分析了脉冲LD巴条侧面泵浦Nd:YAG陶瓷重复脉冲泵浦激光陶瓷温度场分布情况以及达到热动态平衡时陶瓷泵浦面的热形变量。所得研究结果为减弱全固态陶瓷激光器热效应,获得大功率激光输出、提高谐振腔稳定性、改善激光器性能提供了理论依据。
-
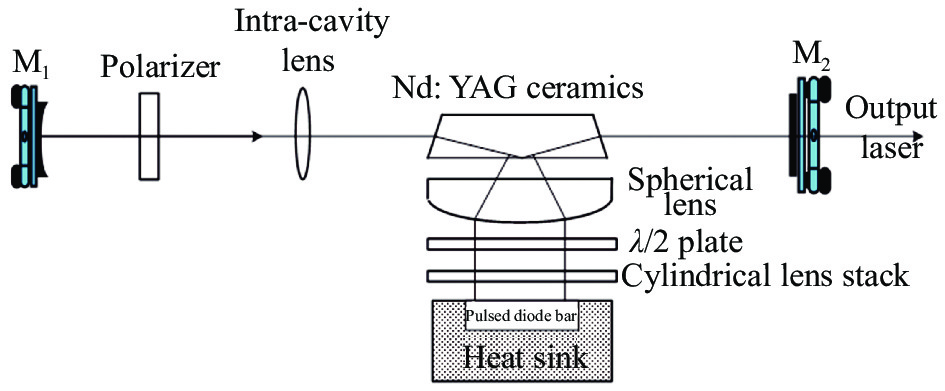
采用LD巴条侧面泵浦的陶瓷全固态激光器,实验装置如图1所示。脉冲LD巴条出射的泵浦光经柱面棱镜准直,以半波片调整其偏振状态与Nd:YAG陶瓷轴相一致,使得激光陶瓷对于泵浦光有较高的吸收效率。由于泵浦激发的反转粒子区与激光振荡模存在着较大的重叠空间,因此脉冲LD巴条侧泵旁掠射反弹结构的陶瓷激光器具有较高的斜效率以及TEM00模输出[7-8]。在一般应用中,透明陶瓷微结构带来的折射率并不影响其透光率,但当方向性极强的激光穿过透明陶瓷时,任何微小的折射都会使光线急转弯,因此采用平—凹驻波谐振腔设计,在激光谐振腔内插入偏振片以及聚焦透镜,可有效补偿热双折射带来的影响。

图 1 脉冲LD巴条侧面泵浦旁掠射反弹结构Nd:YAG陶瓷激光器简图
Figure 1. Schematic diagram of Nd:YAG ceramics with grazing-incidence bounce geometry side-pumped by laser pulsed diode bar
为使激光陶瓷吸收泵浦光产生的热量尽快地散失,依据激光陶瓷几何尺寸以及激光器谐振腔光路,机械加工了热沉装置,结构简图如图2所示。激光陶瓷被夹持在两个L型的铜质支架中,为保持陶瓷与热沉具有一致的热胀,使用紫铜来加工热沉。在激光陶瓷与铜支架接触面涂抹银粉后垫上150 μm厚的铟膜,以保持陶瓷与热沉之间良好的热接触。使用循环水冷方式保持热沉铜块温度为20 ℃。其中Nd:YAG陶瓷尺寸为a mm×b mm×c mm。两个端面a mm×c mm切割双楔10o[9],抛光后蒸镀1064 nm增透膜(R<0.1%)。陶瓷a mm
×b mm面为脉冲LD巴条泵浦的泵浦面,镀808 nm泵浦波长的增透膜(R<0.1%)。为了有效利用泵浦光能量,在泵浦面的对立面镀808 nm波长高反膜(R>99.8%)。上、下两个侧面b mm ×c mm为陶瓷与热沉的接触面。 (1) 脉冲LD巴条侧泵Nd:YAG陶瓷热功率分布
LD巴条由一组单个LD发光元串联排列组成,单个LD发光元之间间距很小,所发光束在其传播方向上相互重叠。入射到激光陶瓷泵浦面(z=0)的光束沿x方向呈超高斯分布,而沿y方向呈均匀分布,长度约为3 mm。其光强分布表达式为:
$$I(x,y,0,t)=\left\{ {\begin{array}{*{20}{c}} {{I_0}{{\rm e}^{ - 2{{\left( {\frac{{{{(x - {x_0})}^2}}}{{{\omega ^2}}}} \right)}^k}}}G\left( t \right)\begin{array}{*{20}{c}} {}&{}&{({y_1} \leqslant y \leqslant {y_2})} \end{array}} \\ {0\begin{array}{*{20}{c}} {}&{}&{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&{(y < {y_1},y > {y_2})} \end{array}} \end{array}} \right.$$ (1) 式中:I0为入射到激光陶瓷泵浦面中心处的光强;x0为泵浦光在竖直方向中心点的位置;ω为泵浦光的超高斯半径;k为超高斯分布阶次;G(t)为LD巴条脉冲时间的包络。
超高斯分布脉冲LD巴条泵浦光中心处光强I0表示为:
$${I_0}=\frac{P}{{({y_2} - {y_1})\int_0^\infty {{{\rm e}^{ - 2{{\left( {\frac{{\left( {x - {x_0}} \right)}}{{{\omega ^2}}}} \right)}^k}}}{\rm d}x} }}$$ (2) 式中:P为入射到激光陶瓷泵浦面的光功率,可用激光功率计测量其大小。
$$P=\int_{{y_1}}^{{y_2}} {\int_0^\infty {{I_0}{{\rm e}^{ - 2{{\left( {\frac{{{{(x - {x_0})}^2}}}{{{\omega ^2}}}} \right)}^k}}}{\rm d}x{\rm d}y} } $$ (3) 当k=1时,泵浦光呈现理想高斯分布状态;当k取2、3、4、···时,泵浦光呈现为所谓“大礼帽”分布状态;当k趋于无穷时,泵浦光呈现为均匀分布状态。
由于脉冲LD巴条泵浦热辐射引起激光陶瓷内掺杂激活离子能级的粒子数反转,若激光陶瓷的光学吸收系数为β,沿z方向传播的泵浦光在激光陶瓷内的光强为:
$$I(x,y,{\textit{z}},t)=I(x,y,0,t){{\rm e}^{ - \beta {\textit{z}}}}$$ (4) 泵浦光传播至激光陶瓷后侧面(z=c)的光强为:
$${I_i}(x,y,c,t)=I(x,y,0,t) \cdot {{\rm e}^{ - \beta c}}={I_0}{{\rm e}^{ - 2{{\left( {\frac{{\left( {x - {x_0}} \right)}}{{{\omega ^2}}}} \right)}^k} - \beta c}}G\left( t \right)$$ (5) 为了提高泵浦光能量的利用率,在其后侧面镀808 nm波长高反膜,经高反膜反射回陶瓷的光强为:
$${I_r}(x,y,z,t)=\sigma {I_0}{{\rm e}^{ - 2{{\left( {\frac{{\left( {x - {x_0}} \right)}}{{{\omega ^2}}}} \right)}^k} - \beta c - \beta (c - z)}}G\left( t \right)$$ (6) 式中:σ为激光陶瓷蒸镀高反膜的反射率。
在激光陶瓷内任意位置的总泵浦光强为入射光与反射光光强之和:
$$ \begin{split} I(x,y,{\textit{z}},t)=&{I_i}(x,y,{\textit{z}},t) + {I_r}(x,y,{\textit{z}},t)=\\ &{I_0}{{\rm e}^{ - 2{{\left( {\frac{{{{(x - {x_{\rm{0}}})}^{\rm{2}}}}}{{{\omega ^2}}}} \right)}^k}}}({{\rm e}^{ - \beta {\textit{z}}}} + \sigma {{\rm e}^{ - \beta c}} \cdot {{\rm e}^{ - \beta (c - {\textit{z}})}}) \end{split} $$ (7) 由于激光陶瓷荧光量子效应和内损耗吸收泵浦光的能量远大于其他原因陶瓷吸收的能量,那么激光陶瓷吸收泵浦光能量产生的热功率密度为:
$$ q(x,y,{\textit{z}},t)=\eta \beta I(x,y,{\textit{z}},t)=\left\{ { \begin{array}{l} {\eta \beta {I_0}{{\rm e}^{ - 2{{\left( {\frac{{{{(x - {x_{\rm{0}}})}^{\rm{2}}}}}{{{\omega ^2}}}} \right)}^k}}}({{\rm e}^{ - \beta {\textit{z}}}} + \sigma {{\rm e}^{ - \beta c}} \cdot {{\rm e}^{ - \beta (c - {\textit{z}})}})G\left( t \right)\begin{array}{*{20}{c}} {({y_1} \leqslant y \leqslant {y_2})} \end{array}}\\ {\begin{array}{*{20}{c}} 0&{}&{\begin{array}{*{20}{c}} \end{array}\begin{array}{*{20}{c}} {}&{}&{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{}&{}&{}&{}&{} \end{array}}&{}&{}&{(y < {y_1},y > {y_2})} \end{array}} \end{array}} \end{array}} \right. $$ (8) 式中:η为热转换系数,η=1−λp/λL,其中,λp为泵浦光波长808 nm,λL为腔内振荡光波长1064 nm。
(2) 激光陶瓷热分析模型满足的边界条件
激光陶瓷被夹在铜支架中,内部热量主要以热传导方式经上、下两侧面散失。由于激光陶瓷x=0面和x=a面温度恒定,设其相对温度为0,得出相对温场u后,再叠加上热沉冷却环境温度。陶瓷泵浦面(z=0)和z=c面以及y=0、y=b两通光面均与空气相接触,因此可设陶瓷的前、后两侧面和左、右两通光面近似绝热。这样侧面泵浦激光陶瓷热模型满足的边界条件为:
$$\begin{array}{*{20}{c}} {u(0,y,{\textit{z}})=0;\begin{array}{*{20}{c}} {_{\begin{array}{*{20}{c}} {}&{} \end{array}}^{}}&{} \end{array}u(a,y,{\textit{z}})=0} \\ {{{\left. {\dfrac{{\partial u(x,y,{\textit{z}})}}{{\partial {{y}}}}} \right|}_{y=0}}=0;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; {{\left. {\dfrac{{\partial u(x,y,{\textit{z}})}}{{\partial {{y}}}}} \right|}_{y=b}}=0} \\ {{{\left. {\dfrac{{\partial u(x,y,{\textit{z}})}}{{\partial {\textit{z}}}}} \right|}_{{\textit{z}}=0}}=0;\;\;\;\;\;\;\;\;\;\;\;\;{{\left. {\dfrac{{\partial u(x,y,{\textit{z}})}}{{\partial {\textit{z}}}}} \right|}_{{\textit{z}}=c}}=0} \end{array}$$ (9) -
在脉冲LD巴条泵浦激光陶瓷的过程中,由于激光陶瓷被强制实施了冷却措施,激光陶瓷存在着两个过程,即脉冲升温阶段和泵浦间期时段。依据热传导Poisson方程,可得其热传导方程:
脉冲升温阶段
$$ \left\{ \begin{array}{l} \dfrac{{\partial {u_{\rm{I}}}\left( {x,y,{\textit{z}},t} \right)}}{{\partial t}} = \dfrac{\lambda }{{\rho {C_p}}}\left( {\dfrac{{{\partial ^2}{u_{\rm{I}}}(x,y,{\textit{z}},t)}}{{\partial {x^2}}} + \dfrac{{{\partial ^2}{u_{\rm{I}}}(x,y,{\textit{z}},t)}}{{\partial {y^2}}} + \dfrac{{{\partial ^2}{u_{\rm{I}}}(x,y,{\textit{z}},t)}}{{\partial {y^2}}} + \dfrac{{\beta \eta {I_0}}}{{\rho {C_p}}}{{\rm e}^{ - 2{{\left( {\frac{{{{(x - {x_{\rm{0}}})}^{\rm{2}}}}}{{{\omega ^2}}}} \right)}^k}}}({{\rm e}^{ - \beta {\textit{z}}}} + \sigma {{\rm e}^{ - \beta c}} \cdot {{\rm e}^{ - \beta (c - {\textit{z}})}}}) \right.\\ {u_{\rm{I}}}(x,y,{\textit{z}}){|_{t = 0}} = 0{\rm{ }} \end{array} (0<t<\tau )\right. $$ (10) 脉冲泵浦间期时段
$$ \left\{ \begin{array}{l}\dfrac{\partial {u}_{\rm{II}}\left(x,y,{\textit{z}},t\right)}{\partial t}=\dfrac{\lambda }{\rho {C}_{p}}\left\{\dfrac{\partial {}^{2}u{}_{{\rm I}{\rm I}}(x,y,{\textit{z}})}{\partial {x}^{2}}+\dfrac{{\partial }^{2}{u}_{{\rm I}{\rm I}}(x,y,{\textit{z}})}{\partial {y}^{2}}+\dfrac{{\partial }^{2}{u}_{{\rm I}{\rm I}}(x,y,{\textit{z}})}{\partial {{\textit{z}}}^{2}}\right\}\begin{array}{cc}& \tau \leqslant t\leqslant T\end{array}\\ \\ {u}_{\rm{II}}\left(x,y,{\textit{z}},t\right){|}_{t=\tau }={u}_{\rm{I}}(x,y,{\textit{z}},\tau )\end{array} \right.$$ (11) 式中:ρ、Cp分别为激光陶瓷的密度、定压比热容;λ为激光陶瓷的热导率;τ为LD脉宽;T为脉冲周期。
依据边界条件公式(9),求解方程得到第一个脉冲泵浦激光陶瓷泵浦时段与泵浦间期温度场的一般解析表达式:
$$ \begin{split} {u}_{\rm{I}}\left(x,y,{\textit{z}},t\right)=&{\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{l=0}^{\infty }\frac{f}{g}(1-{\rm e}^{-gt}){\rm{sin}}\frac{m\pi x}{a}{\rm{cos}}\frac{n\pi y}{b}{\rm{cos}}\frac{l\pi {\textit{z}}}{c}}}}\\ &(0 < t < \tau ) \end{split} $$ (12) $$ \begin{split} {u}_{\rm{II}}\left(x,y,{\textit{z}},t\right)= &{\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{l=0}^{\infty }\dfrac{f}{g}({\rm e}^{g\tau }-1){\rm e}^{-gt}}}}{\rm{sin}}\dfrac{m\pi x}{a}{\rm{cos}}\dfrac{n\pi y}{b}{\rm{cos}}\dfrac{l\pi {\textit{z}}}{c}\\ &{\tau \leqslant t \leqslant T} \end{split} $$ (13) 在得出第一个脉冲在陶瓷形成的温度场后,根据脉冲LD巴条在相邻泵浦过程中前一泵浦周期末的温度与下一泵浦周期起点温度相同这一事实依据,可得到在第i个脉冲在激光陶瓷内形成的温度场:
$$ \begin{split} {u_s}\left( {x,y,{\textit{z}},t} \right) =& \displaystyle\sum\limits_{m = 1}^\infty \displaystyle\sum\limits_{n = 0}^\infty \displaystyle\sum\limits_{l = 0}^\infty \dfrac{f}{g}\left( {\left( { \displaystyle\sum\limits_{i = 0}^{i - 2} {{{\rm e}^{g\left( {iT + \tau } \right)}}} - \displaystyle\sum\limits_{i = 1}^{i - 1} {{{\rm e}^{igT}}} - 1} \right){{\rm e}^{ - gt}} + 1} \right)\cdot\\ &\sin \dfrac{{m\pi x}}{a} \cos \dfrac{{n\pi y}}{b} \cos \dfrac{{l\pi {\textit{z}}}}{c} \\ &{iT \le t \le iT + \tau } {且}i \ge 2 \end{split} $$ (14) $$ \begin{split} {u_j}\left( {x,y,{\textit{z}},t} \right) =& \displaystyle\sum\limits_{m = 1}^\infty \displaystyle\sum\limits_{n = 0}^\infty \displaystyle\sum\limits_{l = 0}^\infty \dfrac{f}{g}\left( { \displaystyle\sum\limits_{i = 0}^{i - 1} {{{\rm e}^{g\left( {iT + \tau } \right)}}} - \displaystyle\sum\limits_{i = 1}^{i - 1} {{{\rm e}^{igT}}} - 1} \right){{\rm e}^{ - gt}}\cdot\\ &\sin \dfrac{{m\pi x}}{a} \cos \dfrac{{n\pi y}}{b} \cos \dfrac{{l\pi {\textit{z}}}}{c} \\ &{iT + \tau \le t \le \left( {i + 1} \right) T{且}i \ge 2} \end{split}$$ (15) 式中:us(x, y, z, t)、uj (x, y, z, t)分别为i (i≥2)个脉冲重复周期后在泵浦阶段与泵浦间隔内的温度场, i为脉冲泵浦次数。
在经历一段时间后,激光陶瓷内温度场达到准热平衡态。准热平衡态时泵浦阶段与泵浦间期陶瓷温度场的解析表达式为:
$$ \begin{split} {u_{{\rm{I}}w}}\left( {x,y,{\textit{z}},t} \right) = & \displaystyle\sum\limits_{m = 1}^\infty \displaystyle\sum\limits_{n = 0}^\infty \displaystyle\sum\limits_{l = 0}^\infty \dfrac{f}{g}\left( {1 + \dfrac{{({{\rm e}^{(1 + N)gT}} - {{\rm e}^{(\tau + Ng)}}){{\rm e}^{ - gt + gNt}}}}{{{{\rm e}^{NgT}} - {{\rm e}^{(N + 1)gT}}}}} \right)\cdot\\ &\sin \dfrac{{m\pi x}}{a}\cos \dfrac{{n\pi y}}{b}\cos \dfrac{{l\pi {\textit{z}}}}{c} \\ &{NT \le t \le NT + \tau } \end{split} $$ (16) $$ \begin{split} {u_{{\rm{II}}w}}\left( {x,y,z,t} \right) =& \displaystyle\sum\limits_{m = 1}^\infty \displaystyle\sum\limits_{n = 0}^\infty \displaystyle\sum\limits_{l = 0}^\infty \dfrac{f}{g}\left( {\dfrac{{({{\rm e}^{g\tau }} - 1){{\rm e}^{g(T - t + NT)}}}}{{{{\rm e}^{gT}} - 1}}} \right)\cdot\\ &\sin \dfrac{{m\pi x}}{a}\cos \frac{{n\pi y}}{b}\cos \dfrac{{l\pi z}}{c} \\ &{NT + \tau \le t \le \left( {N + 1} \right)} T \end{split} $$ (17) 式中:uⅠw(x, y, z, t)、uⅡw(x, y, z, t)分别为准热平衡态泵浦阶段与泵浦间期的温度场;N为脉冲LD巴条的泵浦次数。f、g分别为:
$$ f = \dfrac{{8c{\beta ^2}\eta {I_0}}}{{a\rho {C_p}}}\frac{{\left( {\sin \frac{{n\pi {y_2}}}{b} - \sin \dfrac{{n\pi {y_1}}}{b}} \right)}}{{n\pi }}\frac{{(1 - \sigma {{\rm e}^{ - 2\beta c}} + (\sigma - 1){{\rm e}^{ - \beta c}}{\rm cos}(l\pi ))}}{{{l^2}{\pi ^2} + {c^2}{\beta ^2}}}\int\limits_0^a {{{\rm e}^{ - 2{{\left( {\frac{{{{(x - {x_0})}^2}}}{{{\omega ^2}}}} \right)}^k}}}\sin \frac{{m\pi x}}{a}{\rm d}x} $$ $$g=\frac{\lambda }{{\rho {{\rm{C}}_p}}}\left[ {{{\left( {\frac{{m\pi }}{a}} \right)}^2} + {{\left( {\frac{{n\pi }}{b}} \right)}^2} + {{\left( {\frac{{l\pi }}{c}} \right)}^2}} \right]$$ 式中:m、n、l为正交归一本征函数系确定的正整数。
受激光陶瓷内部温升影响,激光陶瓷发生热膨胀,导致激光器输出功率降低、输出光束的质量变差。
考虑激光陶瓷上、下两个侧面和冷却夹块之间有铟箔衬垫且铟箔较软,因此,激光陶瓷四周近似无外力约束,可将其视为自由热膨胀。为便于分析,在激光陶瓷内部取一个小长方体,其边长分别为
dx、dy、dz,长方体原温度为0(相对),在达到热平衡时的温度为u(x, y, z, t),则其热形变量为: $$ \begin{array}{l} {\rm{d}}{\varGamma _x}=\alpha u(x,y,{\textit{z}},t){\rm{d}}x \\ {\rm{d}}{\varGamma _y}=\alpha u(x,y,{\textit{z}},t){\rm{d}}y \\ {\rm{d}}{\varGamma _{\textit{z}}}=\alpha u(x,y,{\textit{z}},t){\rm{d}}{\textit{z}} \end{array} $$ (18) 式中:α为激光陶瓷热膨胀系数。
-
陶瓷尺寸为2 mm×20 mm×5 mm,脉冲LD巴条侧泵Nd:YAG陶瓷掺钕离子浓度为1.0atm%,其吸收系数为11 cm−1。Nd:YAG陶瓷的热性能参数如表1所示。
表 1 Nd:YAG陶瓷的热性能
Table 1. Thermal performance of Nd:YAG ceramics
Thermal performance Status (300 K) Thermal conductivity/W·cm−1·K−1 0.10 Specific heat/J·g −1·K−1 0.59 Thermal diffusion rate/cm2·s−1 0.046 Thermal expansion/K−1 8.2×10−6 Density/g·cm−3 4.55 泵浦激光选用快轴准直的60 W二极管巴条,调节工作电源固定频率为100 Hz,脉冲泵浦宽度为2 ms,泵浦光束腰半径为150 μm时,由公式(16)、(17)得出重复脉冲一段时间的Nd:YAG陶瓷三维温场分布,如图3所示。
-
泵浦光斑与激光介质内基模的模式匹配方式达到最佳时,激光器可获得较高的光光转换效率且有较高质量的光束输出。图4给出了不同高斯泵浦光斑下Nd:YAG陶瓷受LD巴条脉冲泵浦时泵浦面中心位置上的温度变化。

图 4 不同高斯泵浦腰斑下陶瓷中心温升
Figure 4. Temperature rise of ceramics center with different Gauss pumping for waist spot
当泵浦光斑半径分别为100、150、200、300 μm时,Nd:YAG陶瓷泵浦端面中心位置最高温升分别为31.8、29.6、27.9、25.7 ℃。
-
泵浦输入功率的变化引起了激光介质内温度梯度场分布的变化,产生了热透镜效应,影响了光的输出质量。
图5给出了不同脉冲LD巴条泵浦功率时,Nd:YAG陶瓷泵浦端面中心上的温度变化。当泵浦功率分别取80、60、40、20 W时,Nd:YAG陶瓷的泵浦端面中心的最高温升分别为32.8、29.6、26.4、23.2 ℃。
-
图6给出了不同脉冲宽度对陶瓷内部温度变化的影响。当脉冲宽度分别1、2、3、4 ms时,陶瓷内部最高温升分别为25.5、29.6、32.8、35.6 ℃。
-
在周期脉冲LD巴条泵浦Nd:YAG激光陶瓷下,激光陶瓷内部温度会不断升高,但随着脉冲的增加,激光陶瓷升温幅度降低,最后达到一个热动态平衡。
图7、8给出了热动态平衡时,Nd:YAG陶瓷泵浦端面中心温度在30.2~39.0 ℃之间成锯齿状波并呈现稳定的周期分布。

图 7 非稳态周期脉冲LD巴条泵浦下陶瓷泵浦端面中心温度分布
Figure 7. Temperature distribution of ceramics pump end face center under unsteady periodic pulse LD bar pumping

图 8 陶瓷泵浦中心处热动态平衡时温度变化
Figure 8. Temperature change of the ceramic pump center dural thermal dynamic equilibrium
由图7、8还可以得出,重复脉冲泵浦一段时间后趋于热平衡状态,在脉冲LD巴条泵浦每个周期内都有一个升温和降温过程,所以图7、8中的温度变化呈锯齿状波。
-
当脉冲LD巴条侧面抽运YAG陶瓷时,随着温度的变化,陶瓷端面产生了形变量,泵浦光采用2.1.1节中参数时,图9给出了陶瓷中端面的热形变量随时间呈周期性的变化规律,最大热形变量为0.99 μm,最小热形变量为0.95 μm。陶瓷表面受热后产生形变是激光介质热透镜效应的指标之一,参考文献[10]探讨了形变测量方法,为实验测量激光增益介质受热形变影响提供了实验依据。
-
文中在分析脉冲激光二极管陶瓷激光器实验装置的基础上,建构了激光陶瓷工作热分析模型,利用解析法求解,得出了Nd:YAG陶瓷内部温场及热形变场的一般解析表达式,定量分析了不同泵浦功率、不同光斑半径、不同脉冲宽度泵浦下,Nd:YAG陶瓷器件内部的温度变化,并对陶瓷受热后产生的热形变量进行了数值模拟。文中研究结论为陶瓷激光器热效应研究提供理论依据,同时为全固态激光器激光增益介质选择及理论研究提供参考。
Transient thermal effect of Nd:YAG ceramics with pulsed laser diode bar side-pumped
-
摘要: 为减弱脉冲激光二极管巴条侧面泵浦Nd:YAG陶瓷激光器热效应影响,提高谐振腔稳定性以及改善激光器性能,文中利用热传导理论对脉冲激光二极管巴条侧泵激光陶瓷产生的温升及热形变场进行了解析研究。依据脉冲激光二极管巴条侧面泵浦激光陶瓷工作状态分析,建立契合实际的热分析模型,通过热传导Poisson方程求解,得到单脉冲侧泵激光陶瓷泵浦时段与泵浦间期两个阶段温度场与热形变场的一般解析表达式。定量地分析了脉冲二极管巴条侧面泵浦Nd:YAG陶瓷三维温场分布、重复脉冲泵浦过程中温度场分布,以及不同泵浦参数对温场的影响,定量分析了达到热动态平衡时泵浦面的热形变量。计算结果表明:当泵浦光功率为60 W,重复频率为100 Hz,束腰半径为150 μm,钕离子掺杂质量分数为1.0 %时,Nd:YAG陶瓷泵浦面产生29.6 ℃的温升,泵浦面与通光面产生0.95 μm和0.99 μm的热形变量。激光陶瓷温度场解析方法解决了使用数值分析法造成研究精确度不高的问题,该方法还可以应用到激光系统的其他热问题研究中,为减弱激光系统中的热问题提供了理论依据。Abstract: In order to reduce the thermal effect of Nd:YAG ceramic laser side-pumped by pulsed laser diode bar, improve the stability of resonator and improve the performance of laser, the temperature rise and thermal deformation field generated by pulsed laser diode bar side-pumped laser ceramic were studied analytically by using the heat conduction theory. Based on the analysis of the working state of the laser ceramic side-pumped by pulsed laser diode bar, a thermal analysis model suitable to the actual situation was established, and the general analytical expressions of the temperature field and thermal deformation field in the pumping period and the pumping interval were obtained by solving the Poisson equation of heat conduction. The three-dimensional temperature field distribution of Nd:YAG ceramics pumped by the side of pulsed diode bar, the temperature field distribution in the process of repeated pulse pumping, and the influence of different pumping parameters on the temperature field were analyzed quantitatively. The thermal shape variables on the pump surface were analyzed quantitatively when the thermal dynamic equilibrium was reached. Calculation results show that: when the pump power is 60 W, repetition frequency is 100 Hz, beam waist radius is 150 μm, neodymium ions doped mass fraction is 1.0%, the Nd:YAG ceramic pump surface produces temperature rise of 29.6 ℃, pump surface and smooth surface produce 0.95 μm and 0.99 μm hot shape variables. The analytical method of temperature field of laser ceramics solves the problem of low accuracy caused by numerical analysis method, and it can also be applied to other thermal problems of laser system, which provides a theoretical basis for reducing the thermal problems in laser system.
-
Key words:
- all-solid-state-laser /
- side-pumped /
- Nd:YAG ceramics /
- transient thermal effect /
- analytical analysis
-
表 1 Nd:YAG陶瓷的热性能
Table 1. Thermal performance of Nd:YAG ceramics
Thermal performance Status (300 K) Thermal conductivity/W·cm−1·K−1 0.10 Specific heat/J·g −1·K−1 0.59 Thermal diffusion rate/cm2·s−1 0.046 Thermal expansion/K−1 8.2×10−6 Density/g·cm−3 4.55 -
[1] Li Mi, Hu Hao, Gao Qingsong, et al. Dual concentration doped Nd:YAG composite ceramic slab laser with high power [J]. Acta Optica Sinica, 2017, 37(5): 0514003. (in Chinese) [2] Cheng Siqi, Lei Hong, Jiang Menghua, et al. Study on restraining self-oscillations in Nd:YAG bounce laser [J]. Journal of Optoelectronics· Laser, 2016, 27(8): 787-791. (in Chinese) [3] Yang Haolin, Chen Yue, Jia Fuqiang, et al. Research progress in ceramics lasers [J]. Laser & Optoelectronics Progress, 2020, 57(7): 071610. (in Chinese) [4] Li Mengmeng, Yang Fei, Zhao Shanglong, et al. Study on thermal effect of composite Nd:YAG crystal solid state laser [J]. Laser & Infrared, 2020, 50(1): 42-48. (in Chinese) [5] Li Yao, Li Yang, Wang Chao. Absorption light field of side-pumped Nd:YAG crystal in LD planar arrays [J]. Chinese Optics, 2018, 11(2): 206-211. (in Chinese) doi: 10.3788/co.20181102.0206 [6] Li Long, Xue Biao, Zhang Chunling, et al. Thermal effect analysis of continuous laser assisted hot machining alumina ceramics [J]. Laser & Infrared, 2020, 50(1): 13-16. (in Chinese) [7] Zhi Yin, Li Long, Shi Peng, et al. Temperature field of pulse LD end pumped Nd:YAG crystal [J]. Infrared and Laser Engineering, 2015, 44(2): 492-496. (in Chinese) [8] Yan Yufeng, Yu Yang, Bai Suping, et al. Progress on beam quality control technology of slab lasers [J]. Chinese Optics, 2019, 12(4): 767-782. (in Chinese) doi: 10.3788/co.20191204.0767 [9] Sinofsky E D, Alfrey Anthony J. High efficiency high repetition rate, intra-cavity tripled diode pumped solid state laser, US: 6002695[P]. 1999-12-14. [10] 朱家训, 侯金南. 激光散斑法测量热变形[J]. 光电子·激光, 1983, 3(4): 15-18. -






 下载:
下载: