下载:
-
自涡旋光的旋转多普勒效应被发现以来[1]，基于涡旋光测量目标转速的研究已经成为光学探测领域的热门[2-5]，而由于实验中环境较为理想，测量目标转速往往采用叠加态涡旋光[6-9]，这种光路设计具有简洁易操作、测量目标范围广泛、可以补偿线性运动等优势，但是在工程应用中，远距离传输等原因会造成信号光强度大幅衰减，这使得叠加态涡旋光探测系统的信噪比受到极大的限制，然而相干探测可以很好地解决这一问题[10-12]。
20世纪60年代，Forrest等人发现将不同频率的光束混频可以产生中频信号，为外差探测的发展打下了基础。这种探测技术可以保留振幅、相位和频率的信息，而且具有高灵敏度、高信噪比等优势[13]，所以在实验和工程中都被广泛应用[14-16]。1983年，Yuen等人在外差探测的基础上对光路进行改进，提出了早期的平衡探测结构[17]；1985年，Gregory L. Abbs在平衡探测光路中增加了整形滤波器和放大器，并推导了信噪比的表达式，分析了平衡探测中噪声产生的原因，实验证明平衡探测可以提高本振光利用率，抑制相对强度噪声[18]。在涡旋光旋转多普勒效应进入人们的视野后出现了将上述的相干探测与涡旋光结合的探测方式：2013年，Carmelo通过基于涡旋光的零差探测系统测量了粒子的横向运动[19]；2014年，他又通基于涡旋光以双频平衡探测的方式测量了粒子横向运动的方向[20]，该方法规避了低频噪声的干扰，获得了可观性良好的实验结果；2020年，科罗拉多大学的Anderson教授通过实验揭示了外差探测和干涉条纹探测的机理，实验结果表明外差探测敏感的是信号光的相位，而干涉条纹探测敏感的是强度信息[21]。这些研究一方面拓宽了涡旋光在探测领域的应用范围，另一方面在很大程度上促进了外差探测和平衡探测系统与涡旋光测量目标转速技术的结合，但是这些工作并未深入研究其探测系统的精度与信噪比。为了使涡旋光平衡探测系统走向工程化，文中深入分析了基于涡旋光平衡探测的目标转速测量系统在提升信噪比(SNR)方面的优势，对比基于涡旋光旋转多普勒效应的零差探测与平衡探测两种方案，通过对实验数据分析证明了二者均能实现目标转速高精度测量，且涡旋光平衡探测在信号微弱的情况下信噪比具有明显优势；在此基础上，阐明了涡旋光平衡探测系统中本振光功率对信噪比的影响规律。该研究的相关结论对于推动基于涡旋光的目标转速探测走向工程化应用具有一定的指导意义。
-
单态涡旋光的表达式可以写为：
$$ E(\boldsymbol{r},t) = U(\boldsymbol{r})\exp \left[ {i(2\pi ft + l\theta + k{\textit{z}})} \right] $$ (1) 式中：
$l$ 为信号光的拓扑荷数；$ U(\boldsymbol{r}) $ 表示光的复振幅；$ \boldsymbol{r} $ 为光场空间坐标矢量；$ f $ 表示涡旋光频率；$\theta $ 为涡旋光的方位角；$k = 2\pi /\lambda $ 为涡旋光的波数；${\textit{z}}$ 为光程。当涡旋光光轴对准转速为$\varOmega $ 的目标转轴入射时，散射回来的涡旋光会产生旋转多普勒频移$\Delta f$ [1]：$$ \Delta f=\frac{{l\varOmega }}{{2\pi }} $$ (2) 用复指数函数来表示本振光和信号光的电场，其中信号光为涡旋光，本振光为基模高斯光，二者于合束器相干，产生旋转多普勒频移的信号光电场
$ {E_s} $ 与本振光电场$ {E_l} $ 可以表示为：$$ {E_s}(\boldsymbol{r},t) = {U_s}(\boldsymbol{r})\exp \left\{ {i\left[ {2\pi (f + \Delta f)t + l\theta + k{{\textit{z}}_1}} \right]} \right\} $$ (3) $$ {E_l}(\boldsymbol{r},t) = {U_l}(\boldsymbol{r})\exp \left[ {i(2\pi ft + k{{\textit{z}}_2} + \varphi )} \right] $$ (4) 式中：
${{\textit{z}}_1}$ 和${{\textit{z}}_2}$ 分别为信号光和本振光的光程；$\varphi $ 为本振光超前于信号光的相位；${U_s}(\boldsymbol{r})$ 和${U_l}(\boldsymbol{r})$ 分别为信号光和本振光的复振幅。若二者叠加之后光束由光敏面面积为$A$ 的单源探测器接收，其输出电流可表示为[22]：$$ \begin{split} i(t) =& \beta \displaystyle\iint\limits_A {{{\left| {{E_s}(\boldsymbol{r},t) + {E_l}(\boldsymbol{r},t)} \right|}^2}{{\rm{d}}^2}\boldsymbol{r}} = I_s^{} + I_l^{} + \\ & \beta \displaystyle\iint\limits_A {{U_s}(\boldsymbol{r}){U_l}(\boldsymbol{r})\exp \left\{ {i\left[ {2\pi \Delta ft + k({{\textit{z}}_1} - {{\textit{z}}_2}) + l\theta - \varphi } \right]} \right\}}{{\rm{d}}^2}\boldsymbol{r} \hfill \\ \end{split} $$ (5) 式中：
$\;\beta $ 为探测器的响应度；${I_{\rm{s}}}$ 与${I_l}$ 分别为信号光和本振光导致的直流分量。式中第三项为中频信号，可以发现，中频信号里包含目标转速信息的$\Delta f$ 会在对应的频谱中产生单一的峰值，可以通过提取该峰值的频率大小求取目标转速。在涡旋光平衡探测系统中，设分束镜的反射率
$R$ 和透射率$T$ 为[23]：$$ R = {R_0}\exp \left( {i{\varphi _R}} \right) $$ (6) $$ T = {T_0}\exp \left( {i{\varphi _T}} \right) $$ (7) 式中：
${R_0}$ 和${T_0}$ 分别为反射系数和透射系数；${\varphi _R}$ 和${\varphi _T}$ 分别为反射和透射造成的相位变化。这四个量满足如下关系式：$$ R_0^2 + T_0^2 = 1 $$ (8) $$ \left| {{\varphi _R} - {\varphi _T}} \right| = \frac{\pi }{2} $$ (9) 平衡探测器两个输入端接收到的光信号为：
$$ {E_1} = R{E_s}\left( {\boldsymbol{r},t} \right) + T{E_l}\left( {\boldsymbol{r},t} \right) $$ (10) $$ {E_2} = R{E_l}\left( {\boldsymbol{r},t} \right) + T{E_s}\left( {\boldsymbol{r},t} \right) $$ (11) 设平衡探测器两输入端的光敏面面积分别为
${A_1}$ 和${A_2}$ ，响应度分别为${\alpha _1}$ 和${\alpha _2}$ ，则平衡探测器的两个探测端输出的电流${i_1}$ 和${i_2}$ 分别为：$$ \begin{split} {i_1} =& {\alpha _1}\iint\limits_{{A_1}} {E_1^2}{\rm d^2}\boldsymbol{r} = {\alpha _1}\iint\limits_{{A_1}} {\left[ {R_0^2U_s^2(r) + T_0^2U_l^2(r)} \right]}{{\rm{d}}^2}\boldsymbol{r}+ \\ & 2{\alpha _1}\iint\limits_{{A_1}} {{R_0}{T_0}{U_s}(r){U_l}(r)\cos[ {2\pi \Delta ft + l\theta +}}\\ &{{k\left( {{{\textit{z}}_1} - {{\textit{z}}_2}} \right) - \varphi + \left( {{\varphi _R} - {\varphi _T}} \right)} ]}{{\rm{d}}^2}\boldsymbol{r} \end{split} $$ (12) $$ \begin{split} {i_2} =& {\alpha _2}\iint\limits_{{A_1}} {E_2^2}{{\rm{d}}^2}\boldsymbol{r} = {\alpha _2}\iint\limits_{{A_2}} {\left[ {R_0^2U_s^2(r) + T_0^2U_l^2(r)} \right]}{{\rm{d}}^2}\boldsymbol{r} +\\ & 2{\alpha _2}\iint\limits_{{A_2}} {{R_0}{T_0}{U_s}(r){U_l}(r)\cos [ {2\pi \Delta ft + l\theta +}}\\ & {{k\left( {{{\textit{z}}_1} - {{\textit{z}}_2}} \right) - \varphi - \left( {{\varphi _R} - {\varphi _T}} \right)}]}{{\rm{d}}^2}\boldsymbol{r} \end{split} $$ (13) 公式(12)和公式(13)中，第一个积分项均为直流分量，第二项是带有频移信号的中频交流分量，可以发现两路中频电流相位中
$ {\varphi _R} - {\varphi _T} $ 项前面的符号相反，根据公式(9)可以推得两路电流相位差为$\pi $ 。设平衡探测器输入端具有相同的光敏面面积和响应度，即${A_1} ={A_2} = A$ ，${\alpha _1}={\alpha _2}=\alpha $ ，则平衡探测器输出的光电流为：$$ i = 2\alpha \iint\limits_A {{U_s}\left( \boldsymbol{r} \right){U_l}\left( \boldsymbol{r} \right)\sin \left[ {2\pi \Delta ft + k\left( {{{\textit{z}}_1} - {{\textit{z}}_2}} \right) + l\theta - \varphi } \right]{{\rm{d}}^2}}\boldsymbol{r} $$ (14) 对比公式(5)中的中频信号可以发现，若平衡探测器与普通光电探测器的光敏面面积和响应度相同，则平衡探测的信号强度增加了一倍，并且由于输出电信号为两输入端电流相减，电流中的直流部分与探测器的共模噪声可以很好地被消除，从而提高了系统信噪比。
-
为了研究涡旋光平衡探测系统的信噪比提升效果，实验同时搭建了涡旋光零差探测系统作为对比项。实验中将探测光调制成拓扑荷数为32的涡旋光，本振光为基模高斯光，二者在合束器相干时需要满足以下六个条件：
（1）信号光与本振光有恒定的相位差；
（2）信号光与本振光频率相同或相近；
（3）信号光与本振光在叠加处在某一方向上均有偏振分量；
（4）信号光与本振光光程差小于相干长度；
（5）信号光与本振光光斑尺寸不能相差过大；
（6）信号光与本振光在叠加时夹角不能过大。
根据上述原理和对相干条件的分析，在马赫-增德尔干涉仪的基础上设计了如图1所示的零差探测光路。
图 1 零差探测实验设计图
Figure 1. Design schematic of homodyne detection experiment
波长为632.8 nm的线偏振激光从激光器(Laser, Thorlabs PA21347)出射，经过两个用于光路调整的平面镜M1和M2进入扩束准直系统，扩束准直系统由物镜(OL)、凸透镜(Lens1)和光阑(AP)组成，其中光阑主要用于将光斑周围的杂散光滤除。扩束准直后的光束经过分束立方(BS1)分成探测光和本振光，探测光经过偏振片(P1)和
$\lambda /4$ 波片(QWP)变成圆偏振光，再经过拓扑荷数为32的涡旋波片(VR)变成圆偏振态的单态涡旋光，该涡旋光打到数字微镜空间光调制器(DMD)上，通过在DMD液晶显示器上加载旋转切换的图片来模拟物体旋转。DMD反射的光有许多级次，这里取其中光强度较大的一级作为信号光，信号光经过两个平面镜M3和M4将光路调整回原高度并准直；本振光经过平面镜(M5)与信号光在分束立方(BS2)处叠加，叠加光束经过线偏振片(P2)后发生干涉，并经过透镜(Lens2)汇聚后由光电探测器(PD, Thorlabs PDA100A2)接收并转化为电信号。数据采集卡采集信息后由电脑对信息进行处理分析。根据设计的光路图，搭建的实验光路如图2所示。
图 2 零差探测实验光路
Figure 2. Experimental optical path of homodyne detection
-
进一步，在零差探测光路的基础上设计平衡探测光路，如图3所示。本振光经过平面镜(M5)与信号光在分束立方(BS2)处叠加，其中一路叠加光束经过线偏振片(P2)后发生干涉，由透镜(Lens2)汇聚到平衡探测器(BD, Thorlabs PDB210A/M)其中一个输入端；另一路叠加光束经过平面镜(M6)反射，经过偏振片(P3)发生干涉并由透镜(Lens3)汇聚于BD的另一个输入端。BD的输出信号由数据采集卡采集，并由电脑进行处理分析。需要注意的是，光路末端偏振片P2和P3的偏振方向需要调整到一致，若偏振方向有偏差会导致信号强度下降，过大则会导致光电流平衡被破坏，PC端无法对信号形成响应。
图 3 平衡探测实验设计图
Figure 3. Design schematic of balanced detection experiment
根据图3所示的光路设计图可以搭建如图4所示的基于涡旋光的平衡探测光路，红色虚线框内为平衡探测器的放大图。
图 4 平衡探测实验光路
Figure 4. Experimental optical path of balanced detection
通过实验可以发现DMD所加载的图片相邻帧之间的转角δ在
$ =\dfrac{\pi }{{18}}$ 以内时，均可以探测到旋转多普勒信号，且在此范围内δ的变化不会对信号产生影响。为了使图片旋转2π为一个周期，设置图片相邻帧之间转角固定为δ=$\dfrac{\pi }{{18}} $ 。若DMD图片刷新时间间隔为t0，则物体转速$\varOmega $ 与刷新时间间隔t0的关系为：$$ \varOmega =\frac{\delta }{{{t_0}}} $$ (15) 旋转多普勒频移表达式为：
$$ {f_D} = \frac{{l\varOmega }}{{2\pi }} $$ (16) 式中：
$l$ 为涡旋光的拓扑荷数。将公式(15)代入公式(16)可以得到旋转多普勒频移与刷新时间间隔之间的关系：$$ {f_D}=\frac{l}{{36{t_0}}} $$ (17) 根据公式(17)可以在设置DMD不同的刷新时间间隔时得到旋转多普勒频移的理论值。
-
因为分束立方BS2之后的光路为探测系统的接收端，所以在平面镜M4与分束立方BS2之间设立信号光功率测量点，平面镜M5与BS2之间设置本振光功率测量点。零差探测实验中分别设置信号光功率
${P_s} = 13.5\;\text{μ}{\rm{ W}}$ ，本振光功率${P_L} = 366\;\text{μ}{\rm{ W}}$ ，由于在目标转速较低时频谱会受到DMD谐波的影响，所以在零差探测系统中设置${t_0} = 110\;\text{μ}{\rm{ s}}$ ，使目标转速信号避开谐波。根据式(15)，其对应的目标转速为${\rm{1\;662}}{\rm{.22\;rad/s}}$ 。根据式(17)可以得到理论的旋转多普勒频移${f_D} = 8\;465.6\;{\rm{Hz}}$ 。图5(a)为该目标转速下的频谱图，可以发现零差探测得到的频移结果为8435 Hz，相对误差约为$0.36{\text{%}}$ 。改变DMD的刷新时间，设置${t_0} = 110\;\text{μ}{\rm{ s}}$ ，则对应目标转速为${\rm{1\;586}}{\rm{.66\;rad/s}}$ ，得到理论的旋转多普勒频移${f_D} = $ $ 8\;080.8\;{\rm{Hz}}$ ，根据图5(b)可以得到测得的频移信号为8050 Hz，相对误差约为$0.38 {\text{%}}$ 。
图 5 零差探测转速频谱图
Figure 5. Rotational velocity spectrum of homodyne detection
在平衡探测实验中，调整偏振片P2和P3的偏振方向至二者偏振方向一致，此时旋转多普勒频移信号强度达到最大，分别设置刷新时间间隔
${t_0}$ 为105、110、112、114 μs，对应的目标转速分别为${\rm{1\;662}}{\rm{.22\;}}$ 、${\rm{1\;586}}{\rm{.66\;}}$ 、${\rm{1\;558}}{\rm{.33\;}}$ 、${\rm{1\;530}}{\rm{.99\;rad/s}}$ 。信号光、本振光功率与零差探测相同，理论上对应的旋转多普勒频移分别为8465.6、8080.8、7936.5、7797.3 Hz，通过实验可以得到如图6所示的转速频谱图。从图中可以读出测量得到的旋转多普勒频移分别为8435、8050、7910、7770 Hz，相对误差分别为$0.36{\text{%}}$ 、$0.38{\text{%}}$ 、$0.33{\text{%}}$ 、$0.35{\text{%}}$ 。
图 6 平衡探测转速频谱
Figure 6. Rotational velocity spectrum of balanced detection
可以发现零差探测和平衡探测都可以得到较为准确且信噪比较高的旋转多普勒信号。虽然在测量过程中存在频谱的抖动，但是并不会影响系统的探测精度，而且根据频谱中的旋转多普勒信号可以读出目标转速的大小及其变化。上述测量误差的一个重要诱因是频谱分辨率的大小，若频谱分辨率下降，系统读数误差会变大，进而导致相对测量误差的增大，这在零差探测和平衡探测系统中均不可避免。
为了分析零差探测与平衡探测两种测量方式在测量精度与信噪比方面的差异，下面将在相同频谱分辨率的条件下，探究不同因素对测量精度与信噪比的影响以及信噪比的变化规律。
-
分析探测精度时，保持两种探测方式的信号光和本振光强度相同，光功率大小均为
${P_s} = 13.5\;\text{μ}{\rm{ W}}$ ，${P_L} = 366\;\text{μ}{\rm{ W}}$ 。由于此时两种探测方式接收的信号较强，信号读取不会受到噪声过大的影响，而且对于不同转速的物体，两种探测方式接收到的信号都是相同的，所以二者的探测精度是相同的。图7所示为探测相对误差随转速的变化，随着转速的变化，测量精度会有一定的浮动，但是相对误差不会超过0.5%，且测量高转速时精度变化较为平稳。
图 7 相对误差随转速变化
Figure 7. Relative error changes with rotational velocity
为了深入研究涡旋光平衡探测系统对微弱旋转多普勒信号的探测能力，实验对比不同的信号光功率下零差探测和平衡探测的信噪比。通常信噪比
$ {R_{{\rm{SN}}}} $ 可以表示为：$$ {R_{{\rm{SN}}}} = 10\lg \left( {\frac{{{P_s}}}{{{P_n}}}} \right) $$ (18) 式中：
${P_s}$ 为信号光功率；${P_n}$ 为噪声功率。将公式(18)用电压有效值表示为：$$ {R_{{\rm{SN}}}} = 20\lg \left( {\frac{{{V_s}}}{{{V_n}}}} \right) = 20\left( {\lg {V_s} - \lg {V_n}} \right) $$ (19) 式中：Vs和Vn分别为信号和噪声的电压有效值 。
保证本振光功率
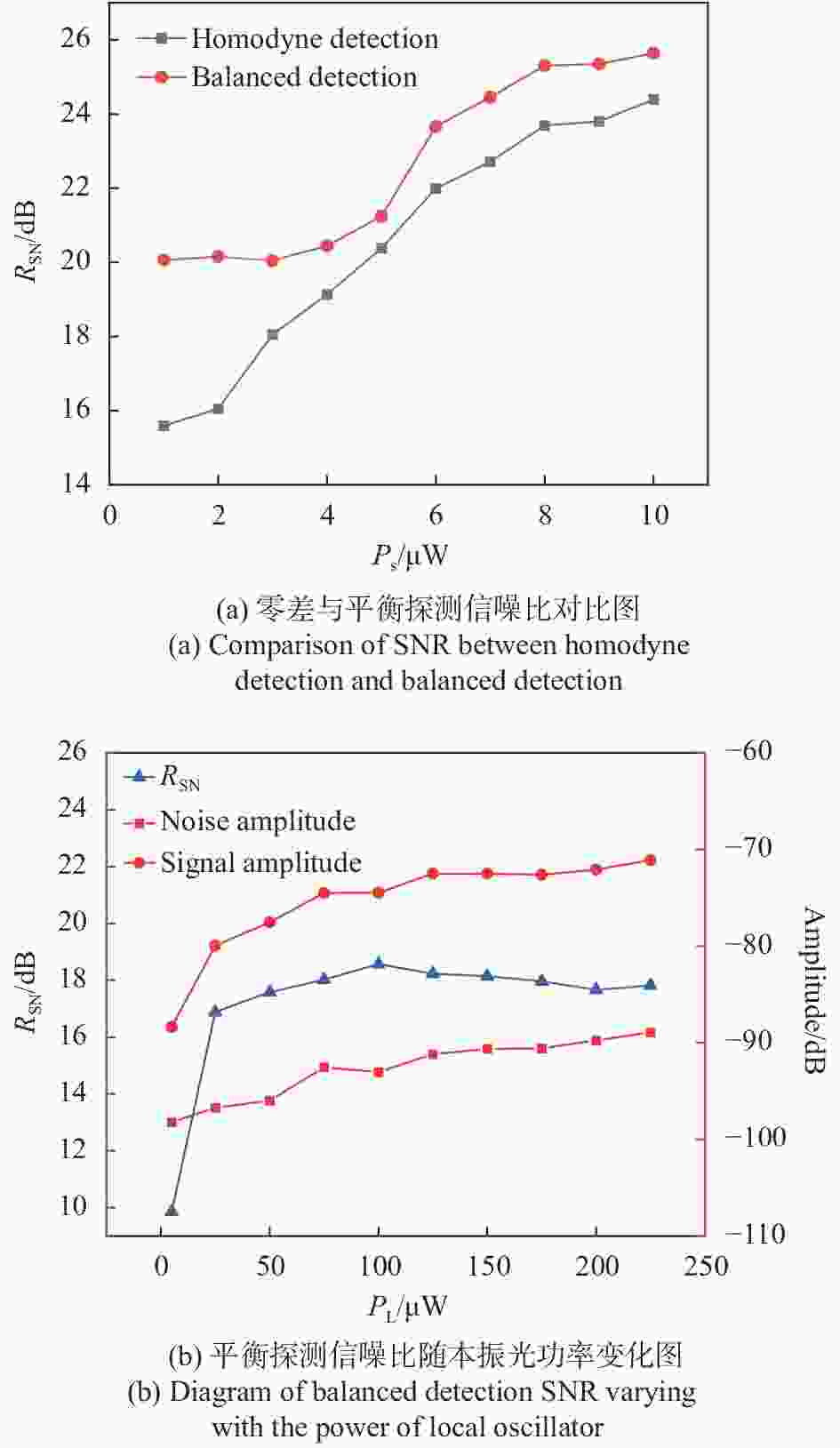
${P_L} = 478\;\text{μ}{\rm{ W}}$ 、${t_0} = 160\;\text{μ}{\rm{ s}}$ 不变，根据公式(19)可以得到实验结果如图8(a)所示，随着信号光功率的增大，平衡探测与零差探测的信噪比都逐渐提升，信号光功率在$4\;\text{μ}{\rm{ W}}$ 以上时，平衡探测信噪比高出零差探测2 dB。但在信号光极其微弱的情况下，平衡探测比零差探测信噪比提高四五分贝，体现出了很明显的优势，其原因在于：共模噪声在信号光强不同时变化不大，当信号光较弱时，普通的零差探测系统中信号强度相对于共模噪声强度较小，而此时平衡探测器消除了大部分共模噪声，并且可以最大程度地利用本振光功率，使得平衡探测比零差探测交流分量幅值提高一倍，这样便拉开了二者的信噪比差距。在回波信号极其微弱时，涡旋光零差探测的系统中的旋转多普勒信号几乎消失在噪声当中，而涡旋光平衡探测的系统却依然能够观测到该信号，这极大地拓宽了涡旋光转速探测的测量条件，对于远距离目标探测和微弱信号的提取都具有一定的工程意义。
图 8 信噪比分析图
Figure 8. Analysis of SNR
在平衡探测系统中，本振光功率也对信噪比有着一定的影响，如图8(b)所示，展示了在信号光功率一定的情况下，信噪比、电信号强度和噪声强度随本振光功率的变化规律。由于文中侧重于弱信号探测，实验中维持信号光功率
${P_s} = 0.3\;\text{μ}{\rm{ W}}$ ，本振光功率从$5\;\text{μ}{\rm{ W}}$ 增加到$225\;\text{μ}{\rm{ W}}$ ，同时为了保证数据的可信度和准确性，测量时在相同条件下获取多组数据，取每组数据信噪比的平均值作为结果。从图8(b)中可以看出噪声强度随本振光功率呈线性变化，而本振光的增强会引起相对强度噪声的非线性变化和散粒噪声的线性变化[24]，说明涡旋光平衡探测系统抑制了大部分的相对强度噪声，使得相对强度噪声的强度远小于散粒噪声强度，因此测量过程中可以忽略相对强度噪声和热噪声的影响，主要考虑散粒噪声对探测系统信噪比的影响。从信噪比变化曲线可以看出，本振光在
$100\;\text{μ}{\rm{ W}}$ 时，信噪比达到最大值，本振光功率超过该最大值点后，信噪比维持在一个平稳的水平不会增加，且伴有小幅度下降的趋势。总体来说，随着本振光强增加，信噪比的变化分为两个阶段：第一阶段为信噪比随本振光功率上升阶段，从图8(b)中的信号和噪声强度变化可以看出，该阶段中由于本振光功率逐渐增大，散粒噪声也逐渐增大，但是本振光对信号的增强作用远大于逐渐增强的散粒噪声对信噪比的抑制作用，所以信噪比变化趋势呈上升状态；当本振光功率增加到一定程度，其对信号的增强作用已达到饱和状态，但散粒噪声还会继续增大，于是进入第二阶段——平台阶段，图中显示该阶段信号强度没有明显增大，此时信噪比还是主要受到散粒噪声的影响，但是影响幅度较小，信噪比整体呈微向下的趋势。 -
文中从工程的角度出发，对涡旋光平衡探测和零差探测两种探测方式在精度和信噪比两方面做出了对比分析：通过在不同转速下的对比可以发现二者探测精度相同且相对误差可以控制在0.5%以内，达到了较高的测量精度且精度变化较为平稳；涡旋光平衡探测系统在探测微弱信号时具有明显优势，其信噪比相对于零差探测提高了4~5 dB，大幅提高了其信号提取的能力。在信噪比随本振光的变化规律方面，文中分析了信号强度、噪声强度和信噪比在本振光功率增强时的变化情况，发现信噪比随本振光功率的变化主要分为两个阶段，在两个阶段的交界点信噪比可以得到最大幅度的增强，并且阐明了信噪比变化的原因。此研究从工程应用角度解决了基于涡旋光的目标转速探测系统在接收微弱信号时信噪比过低的问题，不仅对基于涡旋光的旋转目标转速测量技术的工程化起到了促进作用，而且对涡旋光相干探测领域的发展具有潜在价值。
Analysis of rotational velocity measurement accuracy and signal-to-noise ratio of balanced detection based on vortex beam (Invited)
-
摘要: 对于基于叠加态涡旋光和涡旋光零差探测等传统转速测量方式，光的远距离传输和发散等原因造成的信号光衰减会导致探测系统无法准确提取信号，而涡旋光平衡探测系统可以解决这一难题，但是以往的研究对该探测系统的精度和信噪比鲜有分析，这一定程度上限制了其工程化的进展。首先将零差探测系统作为对比项，通过分析不同转速下涡旋光平衡探测系统和零差探测系统测量精度的变化情况，证明了二者均可实现高精度测量，其次通过对比在不同信号光功率下二者的信噪比(SNR)，发现了在测量微弱信号时涡旋光平衡探测系统具有明显优势；最后，通过分析不同本振光功率对信噪比造成的影响，揭示了平衡探测信噪比和本振光功率之间的关系，阐明了信噪比随本振光功率变化的原因。Abstract: For traditional velocity detection method like superposition state vortex beam detection and vortex beam homodyne detection, the optical attenuation of the signal caused by long-distance transmission and light divergence would lead to that the detection system can not extract the signal accurately. However, the balanced detection based on vortex beam can solve this problem. But there is little analysis about accuracy and signal-to-noise ratio (SNR) of this detection system, which limits the engineering development of the detection system to a certain extent. Firstly, the homodyne detection was set as comparative item. By analyzing the accuracy change condition of balanced detection and homodyne detection based on vortex beam under different rotational velocity, it was verified that both of them can measure accurately. Secondly, it could be found that the balanced detection had significant advantage when signal light power was low by comparing the SNR of both with different signal light power. Finally, the relation of SNR of the balanced detection and local-oscillator power was revealed by analyzing the effect of SNR on different local-oscillator powers. And the cause of SNR changing with local-oscillator power was clarified.
-
Key words:
- vortex beam /
- signal-to-noise ratio /
- accuracy /
- balanced detection /
- homodyne detection /
- rotational Doppler effect
-
[1] Padgett M. Detection of a spinning object using light's orbital angular momentum [J]. Science, 2013, 2(5): 764-768. [2] Zhang W, Gao J, Zhang D, et al. Free-space remote sensing of rotation at the photon-counting level [J]. Physical Review Applied, 2018, 10(4): 044014. [3] Zhang Z, Cen L, Zhang J, et al. Rotation velocity detection with orbital angular momentum light spot completely deviated out of the rotation center [J]. Opt Express, 2020, 28(5): 6859-6867. doi: 10.1364/OE.380324 [4] Fu S, Wang T, Zhang Z, et al. Non-diffractive Bessel-Gauss beams for the detection of rotating object free of obstructions [J]. Opt Express, 2017, 25(17): 20098-20108. doi: 10.1364/OE.25.020098 [5] Fu Ziling, Wang Zhi, Cui Can, et al. Angular velocity measurement based on rotational Doppler effect of vortex beam [J]. Laser & Optoelectronics Progress, 2019, 56(18): 180501. (in Chinese) [6] Qiu S, Liu T, Li Z, et al. Influence of lateral misalignment on the optical rotational Doppler effect [J]. Appl Opt, 2019, 58(10): 2650-2655. doi: 10.1364/AO.58.002650 [7] Qiu S, Liu T, Ren Y, et al. Detection of spinning objects at oblique light incidence using the optical rotational Doppler effect [J]. Opt Express, 2019, 27(17): 24781-24792. doi: 10.1364/OE.27.024781 [8] Qiu S, Ren Y, Liu T, et al. Detecting the speed of a rotational cylinder based on Doppler effect of optical vortex [J]. Acta Optica Sinica, 2020, 40(20): 2026001. (in Chinese) doi: 10.3788/AOS202040.2026001 [9] Li Z, Liu T, Ren Y, et al. Direction-sensitive detection of a spinning object using dual-frequency vortex light [J]. Opt Express, 2021, 29(5): 7453-7463. doi: 10.1364/OE.418192 [10] Guo Liren, Hu Yihua, Lizheng, et al. Influence of Local Oscillate power on micro-motion balanced heterodyne detection for Lidar [J]. Infrared and Laser Engineering, 2015, 44(10): 2933-2937. (in Chinese) doi: 10.3969/j.issn.1007-2276.2015.10.011 [11] Fink D. Coherent detection signal-to-noise [J]. Appl Opt, 1975, 14(3): 689-690. doi: 10.1364/AO.14.000689 [12] Liang Hexi, Dai Yonghong, Ai Yong, et al. Design and test of space optical coupling balance detector [J]. Infrared and Laser Engineering, 2017, 46(3): 0320002. (in Chinese) [13] Xiao Shilin, Zeng Qingji. Application of optical coherent detection [J]. Optical Coherent Technology, 2003(11): 28-31. (in Chinese) [14] Zhong Zhi, Tan Jiubin, Ma Hongwen, et al. Study on fast ultra-precision measurement model in laser heterodyne interferometry [J]. Acta Optica Sinica, 2005, 25(6): 791-794. (in Chinese) doi: 10.3321/j.issn:0253-2239.2005.06.015 [15] Gao Long, Wang Chunhui, Li Yanchao, et al. Theory analysis of polarization mixing error in dual-balanced heterodyne detection [J]. Infrared and Laser Engineering, 2010, 39(3): 422-426. (in Chinese) doi: 10.3969/j.issn.1007-2276.2010.03.010 [16] Li Yu, Zhang Shu, Zhou Jian, et al. Application of dual-balanced detection in laser velocimeter [J]. High Power Laser and Particle Beams, 2016, 28(10): 101004. (in Chinese) doi: 10.11884/HPLPB201628.160021 [17] Yuen H P, Chan V W. Noise in homodyne and heterodyne detection: errata [J]. Opt Lett, 1983, 8(6): 345. doi: 10.1364/OL.8.000345 [18] Abbas G, Chan V, Ting Y. A dual-detector optical heterodyne receiver for local oscillator noise suppression [J]. Journal of Lightwave Technology, 1985, 3(5): 1110-1122. doi: 10.1109/JLT.1985.1074301 [19] Rosales-Guzman C, Hermosa N, Belmonte A, et al. Experimental detection of transverse particle movement with structured light [J]. Sci Rep, 2013, 3: 2815. doi: 10.1038/srep02815 [20] Rosales-Guzman C, Hermosa N, Belmonte A, et al. Direction-sensitive transverse velocity measurement by phase-modulated structured light beams [J]. Opt Lett, 2014, 39(18): 5415-5418. doi: 10.1364/OL.39.005415 [21] Anderson A Q, Strong E F, Heffernan B M, et al. Detection technique effect on rotational Doppler measurements [J]. Opt Lett, 2020, 45(9): 2636-2639. doi: 10.1364/OL.390425 [22] 李玉. 基于平衡探测器的光外差探测系统研究 [J]. 长沙: 国防科技大学, 2015. Li Yu. Research on the heterodyne detection system based on balanced detector[D]. Changsha: National University of Defense Technology, 2015. (in Chinese) [23] 熊大明. 光外差平衡探测关键技术研究 [D]. 武汉: 武汉邮电科学研究院, 2020. Xiong Daming. Research on key techniques of optical heterodyne balance detection[D]. Wuhan: Wuhan Research Institute of Posts and Telecommunications, 2020. (in Chinese) [24] Liang Hexi, Dai Yonghong, Ai Yong, et al. Influence of local oscillator power on sensitivity of coherent detection of space balanced detection [J]. Optics and Precision Engineering, 2017, 25(2): 334-341. (in Chinese) doi: 10.3788/OPE.20172502.0334 -
点击查看大图
图(8)
计量
- 文章访问数: 390
- HTML全文浏览量: 163
- PDF下载量: 59
- 被引次数: 0
