下载:
-
衍射成像光谱系统采用轴向色散二元光学衍射元件，能够同时实现光谱色散以及光学面阵成像的功能。传统光栅类型成像光谱系统采用线阵扫描的成像模式，使用的衍射元件色散方向垂直于光线传播方向。而衍射型成像光谱仪采用的衍射元件，其色散方向沿着光线传播方向，不同光谱对应不同的最佳焦面位置。沿轴向移动探测器到达相应光谱的最佳焦面位置并进行面阵成像，可获取目标的一系列空间和光谱混叠信息，采用衍射光谱数据解调算法可反演复原出目标光谱数据信息[1-2]。因为系统没有狭缝，提升了光的利用效率，提高了光谱探测的信噪比，进而有利于促进光谱成像系统实现小型化，提升光谱成像系统对目标进行探测识别的效能。
国内外学者对衍射成像光谱仪开展了相关研究，基于单通道方案进行模拟仿真，针对简单图形目标或气体目标进行光谱成像实验。太平洋高技术公司Michele Hinnrichs研究了应用于气体探测的衍射系统，包含SWIR、MWIR和LWIR红外谱段[3]；美国陆军实验室研究了Warlock成像光谱仪长波红外谱段[4]；南京理工大学张茗琪等采用改进的逆滤波算法，将逆滤波函数进行正则化，降低图像复原中噪声产生的影响，通过模拟仿真和实验测试，表明复原得到的图像清晰度和光谱曲线精度都得到了提升[5]。浙江大学梁靖宇研究了光谱成像系统中的衍射光学元件设计方法、目标光谱信息重构算法，搭建了简单光路并对水杯进行衍射成像[6]；苏州大学的曾文明等采用正则化方法进行衍射透镜成像光谱仪图像复原，附加假设的条件或经验预知项，利用计算机模拟乙烷和异戊二烯气体的衍射成像并进行复原，模拟实验表明，正则化方法能够抑制噪声的干扰进而有效复原出气体光谱图像[7]；南京理工大学王旭从局部平滑性出发，考虑光谱平滑性和空间平滑性，对衍射解算模型进行改进，采用了交替方向乘子法，有效抑制了系统噪声，并且保证了求解速度，在保留边缘信息的情况下改善了锯齿形状的光谱失真[8]。
国内外现有研究主要针对单通道衍射光谱成像系统开展理论研究和系统设计，对简单图形目标或光谱特征已知的气体目标进行模拟仿真和光谱成像实验。而真实成像系统存在噪声、制造误差、装调误差、定标误差等因素，难以准确获取系统的衍射色散参数。目标景物越复杂、系统误差因素越多，单通道方案的光谱解算效果越差。针对复杂景物光谱数据获取和反演，文中设计了一套双通道可见近红外衍射计算成像光谱系统，在常规单通道衍射成像光谱成像系统的基础上，增加一路全色灰度相机成像，可以为衍射成像通道提供先验知识，将两个通道的数据进行联合处理，可提升复杂景物光谱数据反演效果和反演精度。利用仿真程序模拟了系统衍射光谱成像过程。针对复杂光谱场景进行仿真成像和光谱解调，对传统光谱解调算法进行了优化。搭建了可见近红外衍射光谱成像实验原理验证装置，对卫星模型和色卡分别进行了成像实验，得到光谱数据复原，计算了复原精度。通过衍射计算成像原理分析、模拟仿真和原理实验，验证了系统原理的正确性，能够反演得到精度优于90%的复杂景物光谱数据。
-
衍射光谱成像系统使用的衍射光学元件是多台阶衬底结构的高衍射效率元件，有利于光学成像系统实现微型化、轻小型化和高集成化。双通道衍射计算光谱成像系统包括衍射成像光谱系统以及全色灰度相机成像系统。衍射光谱成像系统的核心主要部件是衍射成像透镜，在对入射光线聚焦成像的同时还能产生轴向的色差。衍射光学具有独特的色散特性，色散与波长有关[9-13]。衍射光学元件不同波长焦距与入射光波长成反比：
$$ f(\lambda ) = \frac{{{\lambda _0}{f_0}}}{\lambda } $$ (1) 式中：f0为设计波长λ0的焦距，即设计焦距。
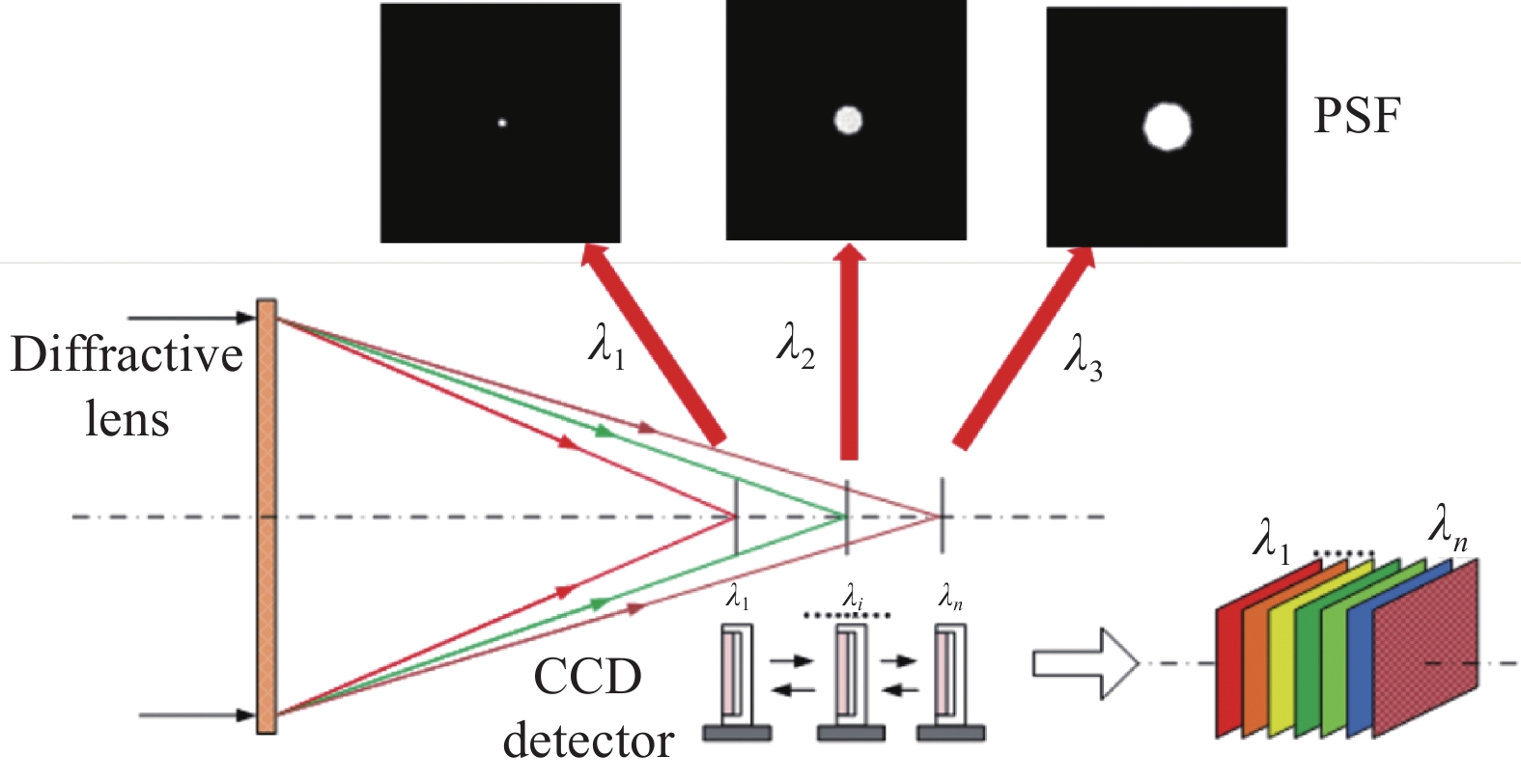
如图1所示，衍射成像光谱系统的色散方向是沿着光纤传播方向，在色散空间上产生一定数量的光谱切片，因此光谱切片的序列方向即为光轴方向。在光轴方向上，不同切片处的点扩展函数PSF表示相应准焦和离焦光谱切片的成像效应、清晰和模糊的程度，PSF对光谱分辨率、带宽起到决定性作用。
图 1 衍射成像光谱系统示意图
Figure 1. Schematic diagram of diffraction imaging spectrometer system
光谱分辨率是光谱仪系统的重要参数，用f/#表示系统的F数，则波长λ的光谱分辨率表达式为：
$$ \Delta \lambda = \frac{{{\lambda ^2}}}{{{\lambda _0}{f_0}}}\Delta = \frac{{{\lambda ^2}}}{{{\lambda _0}{f_0}}} \cdot 8\lambda {({f \mathord{\left/ {\vphantom {f \# }} \right. } \# })^2} = \frac{{8{\lambda _0}\lambda }}{{{f_{_0}}}}{({f \mathord{\left/ {\vphantom {f \# }} \right. } \# })^2} $$ (2) 衍射效率是衍射成像系统里的关键指标，针对指定的位相函数，在制备微结构单元衍射面时，衍射面的第m级次的衍射效率计算方法如公式（3），N为衍射元件DOE的级数，当N取6时衍射效率接近90%[9-10]。
$$ \eta _m^N = \frac{1}{{{N^2}}} \cdot \dfrac{{{{\sin }^2}\left[ {\pi \left( {1 - \dfrac{{{\lambda _0}}}{\lambda }} \right)} \right]}}{{{{\sin }^2}\left[ {\dfrac{\pi }{N}\left( {1 - \dfrac{{{\lambda _0}}}{\lambda }} \right)} \right]}} \cdot {{{\rm{sinc}}} ^2}\left( {\dfrac{m}{N}} \right) $$ (3) -
衍射光谱系统成像的光谱重构有很多种方法[5-11]，文中针对光谱图像函数建立量化模型，将光谱图像数据立方体看作x，y，z(λ)的连续函数，图像在x，y方向经过面阵探测器采样，探测器沿光轴z方向在不同的光谱聚焦点位置进行扫描成像。数字量化表征目标信号图像函数，用h()表示点扩散函数。三维矩阵方程如下：
$$ \begin{gathered} i\left( {{x_i},{y_i},{z_i}} \right) = \hfill \\ \int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {o\left( {x,y,z} \right)} } } h\left( {{x_i} - x,{y_i} - y,{z_i} - z} \right){\rm{d}}x{\rm{d}}y{\rm{d}}z \hfill \\ \end{gathered} $$ (4) 对x、y、z进行离散化处理，可将方程（4）的积分形式改写为求和形式，以四种光谱色散为例，用o(x, y)表示每个光谱位置的准焦图像，h(x, y)表示相应的准焦和离焦点扩散函数，探测器分别在四种光谱位置探测，得到的四种信号能量可表示为：
$$ \begin{split}&{i}_{\text{1}}\left({x}\text{，}{y}\right)\text={h}_{11}\left({x}\text{，}{y}\right)\ast {o}_{1}\left({x}\text{，}{y}\right)+{h}_{12}\left({x}\text{，}{y}\right)\ast {o}_{2}\left({x}\text{，}{y}\right) +\\&{h}_{13}\left({x}\text{，}{y}\right)\ast {o}_{3}\left({x}\text{，}{y}\right)+{h}_{14}\left({x}\text{，}{y}\right)\ast {o}_{4}\left({x}\text{，}{y}\right)\\& {i}_{2}\left({x}\text{，}{y}\right)\text={h}_{21}\left({x}\text{，}{y}\right)\ast {o}_{1}\left({x}\text{，}{y}\right)+{h}_{22}\left({x}\text{，}{y}\right)\ast {o}_{2}\left({x}\text{，}{y}\right) +\\&{h}_{23}\left({x}\text{，}{y}\right)\ast {o}_{3}\left({x}\text{，}{y}\right)+{h}_{24}\left({x}\text{，}{y}\right)\ast {o}_{4}\left({x}\text{，}{y}\right)\\& {i}_{3}\left({x}\text{，}{y}\right)\text={h}_{31}\left({x}\text{，}{y}\right)\ast {o}_{1}\left({x}\text{，}{y}\right)+{h}_{32}\left({x}\text{，}{y}\right)\ast {o}_{2}\left({x}\text{，}{y}\right) +\\&{h}_{33}\left({x}\text{，}{y}\right)\ast {o}_{3}\left({x}\text{，}{y}\right)+{h}_{34}\left({x}\text{，}{y}\right)\ast {o}_{4}\left({x}\text{，}{y}\right)\\& {i}_{4}\left({x}\text{，}{y}\right)\text={h}_{41}\left({x}\text{，}{y}\right)\ast {o}_{1}\left({x}\text{，}{y}\right)+{h}_{42}\left({x}\text{，}{y}\right)\ast {o}_{2}\left({x}\text{，}{y}\right) +\\&{h}_{43}\left({x}\text{，}{y}\right)\ast {o}_{3}\left({x}\text{，}{y}\right)+{h}_{44}\left({x}\text{，}{y}\right)\ast {o}_{4}\left({x}\text{，}{y}\right)\end{split} $$ (5) 上述方程描述了探测器在每个位置处探测得到的混叠光谱信号，每一光谱目标都与对应位置处的点扩展函数卷积，混叠光谱图像可以看作是所有卷积叠加的结果。
能量表达式（5）经过傅里叶变换后，用矩阵表达的形式为：
$$ \begin{split}&\left[\begin{array}{c}{I}_{\text{1}}\left(\xi \text{，}\zeta \right)\\ {I}_{\text{2}}\left(\xi \text{，}\zeta \right)\\ {I}_{\text{3}}\left(\xi \text{，}\zeta \right)\\ {I}_{\text{4}}\left(\xi \text{，}\zeta \right)\end{array}\right]\text=\\ &\left[\begin{array}{cccc}{H}_{11}\left(\xi \text{，}\zeta \right)& {H}_{12}\left(\xi \text{，}\zeta \right)& {H}_{13}\left(\xi \text{，}\zeta \right)& {H}_{14}\left(\xi \text{，}\zeta \right)\\ {H}_{21}\left(\xi \text{，}\zeta \right)& {H}_{22}\left(\xi \text{，}\zeta \right)& {H}_{23}\left(\xi \text{，}\zeta \right)& {H}_{24}\left(\xi \text{，}\zeta \right)\\ {H}_{31}\left(\xi \text{，}\zeta \right)& {H}_{32}\left(\xi \text{，}\zeta \right)& {H}_{33}\left(\xi \text{，}\zeta \right)& {H}_{34}\left(\xi \text{，}\zeta \right)\\ {H}_{41}\left(\xi \text{，}\zeta \right)& {H}_{42}\left(\xi \text{，}\zeta \right)& {H}_{43}\left(\xi \text{，}\zeta \right)& {H}_{44}\left(\xi \text{，}\zeta \right)\end{array}\right] \times \\ & \left[\begin{array}{c}{O}_{1}\left(\xi \text{，}\zeta \right)\\ {O}_{2}\left(\xi \text{，}\zeta \right)\\ {O}_{3}\left(\xi \text{，}\zeta \right)\\ {O}_{4}\left(\xi \text{，}\zeta \right)\end{array}\right]\end{split} $$ (6) 式中：I1、I2、I3、I4是探测器在不同光谱位置处探测得到的信号。不同光谱位置处的准焦和离焦点扩散函数H()可通过系统标定得到，通过逆运算即可求得光谱信号O1、O2、O3、O4。
$$ O\left( {\xi ,\zeta } \right) = {H^{ - 1}}\left( {\xi ,\zeta } \right)I\left( {\xi ,\zeta } \right)$$ (7) 实际定标过程存在误差，系统的色散参数难以完全准确测试，并且成像过程存在噪声，这些都会带来解算误差。通过增加一路全色通道，给解算过程提供附加信息，提升解算精度。全色信息为SPAN，全色信息是所有光谱信息叠加后的总信息，即SPAN= O1+O2+O3+O4，可作为附加信息进行联合解算。
每种离焦量有相应的点扩展函数，对点扩展函数进行傅里叶变换，将变换后的点扩展函数组成块矩阵。当光谱通道数量较多、离焦量较大时，矩阵中的某些块近似为零，导致矩阵奇异。求解奇异矩阵的逆矩阵是解决线性最小二乘问题，可采用SVD奇异值分解方法，任意M×N矩阵，行数M≥列数N，进行奇异值分解的表达式为：
$$ {H^{ - 1}} = V\left[ {diag(1/{w_i})} \right] \cdot {U^{\rm{T}}} $$ (8) 式中：w为奇异值。对w进行变换，附加规则滤波器，可有效减小系统噪声对解算的影响。将1/w变换为：
$$ {1 \mathord{\left/ {\vphantom {1 w}} \right. } w} = {w \mathord{\left/ {\vphantom {w {\left( {{w^2} + {a^2}} \right)}}} \right. } {\left( {{w^2} + {a^2}} \right)}}$$ (9) 将SVD代入重建方程（7），可得到：
$$ \begin{split} O(\xi ,\zeta ) =& V(\xi ,\zeta ) \times \left[ {diag\left( {\frac{{w(\xi ,\zeta )}}{{{w^2}(\xi ,\zeta ) + {\alpha ^2}}}} \right)} \right] \times \\ &{U^{\rm{T}}}(\xi ,\zeta ) \times I(\xi ,\zeta ) \end{split} $$ (10) -
仿真输入为15个谱段的魔方图像，520~800 nm每20 nm一个谱段，利用理论PSF对15个谱段进行卷积叠加得到仿真图，每个准焦谱段和离焦谱段的理论PSF如图2所示。
图 2 理论PSF (520~800 nm, 15个谱段)
Figure 2. Theory PSF (520-800 nm, 15 wavebands)
仿真得到每个焦面处的混叠衍射图像，每个混叠图像是一个准焦谱段信息和14个离焦谱段信息的混合信息，即衍射通道探测器获取得到的图像效果，如图3所示。
图 3 仿真每个焦面处的混叠衍射图像
Figure 3. Each mixed diffractive image in corresponding focal plane
利用理论PSF和仿真模拟得到的15个谱段混叠图像以及全色通道图像进行光谱解算，如图4所示。
图 4 每个谱段解算效果
Figure 4. Each demodulation spectral image
将解算出的每个谱段数据与原始输入光谱数据进行对比，可得到解算平均灰度误差为3.2 DN，解算结果与原始输入基本保持一致。图5为740 nm解算结果，灰度误差为2.7 DN。
图 5 谱段740 nm解算误差
Figure 5. Demodulation error of 740 nm
-
为验证文中提出的双通道衍射成像光谱仪系统的成像性能，搭建了实验装置进行成像实验，如图6所示，验证双通道衍射光谱成像的原理可行性，检验衍射光谱成像的性能和解算效果。衍射通道和全色灰度通道采用相同的光学成像镜头和CCD探测器。实验装置前端为衍射透镜，后端为光学聚焦成像镜头和CCD探测器，探测器在导轨上轴向移动采集每个位置处的混叠光谱图像信息，记录输入光谱波段和相应的探测器位置。如图7所示，采用卫星模型和色卡作为成像目标，衍射透镜实现光谱色散的轴向展开，定标各谱段成像位置，移动探测器，分别在每个谱段的准焦位置获得输出的混叠光谱图像数据。
图 6 双通道系统实验装置
Figure 6. Experimental prototype of the double channels system
图 7 成像目标（场景1和场景2）
Figure 7. Imaging targets (scene one and scene two)
系统主要参数：
(1) 衍射主镜：口径200 mm；
(2) 光学成像镜头：焦距300 mm；
(3) 探测器：像元尺寸12 μm，规模1024×1024；
(4) 待测光谱波段范围：可见近红外450~800 nm，光谱间隔10 nm。
真实成像系统的衍射色散情况复杂，准焦光谱信息与离焦光谱信息在空间上连续变化，每个谱段的衍射效率、成像质量均存在差异，点扩散函数PSF用来表征光学成像特性。需要通过系统定标获得每个谱段的准焦以及离焦的PSF。利用小孔以及窄带滤光片测试得到系统的PSF参数，每个谱段有一个准焦PSF以及35个离焦PSF，36个谱段的PSF总数量为36×36。衍射通道有36个成像图像，灰度通道有一个成像图像，图8展示了衍射通道的三个成像效果和一个灰度通道成像效果。利用PSF参数和双通道数据对实验得到的450~800 nm混叠光谱数据进行光谱复原，结果如图9和图10所示。
图 8 三个衍射通道与一个灰度通道的成像效果
Figure 8. Imaging effect of three diffraction channels and one grayscale channel
图 9 场景1的重构光谱数据
Figure 9. Reconstructed spectral data of scene one
图 10 场景2的重构光谱数据
Figure 10. Reconstructed spectral data of scene two
利用海洋光学光谱仪测试色板的光谱曲线作为标准谱线，与复原得到的光谱数据进行对比，得到a1、a2、a3、b1、b2、b3、c1、c2、c3、d1、d2、d3
等12个色卡颜色区域的光谱曲线。用d3作为基准，计算其他11个色卡颜色区域的光谱曲线复原精度。 使用色卡验证光谱复原精度有其局限性，因为不同色卡的光谱曲线响应差异大，部分谱段响应极低，信噪比极低，计算出来的误差偏差较大，造成整体复原精度明显下降。按照误差计算理论，实际计算时去除误差偏离极大的数据点。图11为重构的光谱数据精度，考虑全部光谱数据时平均复原精度80.4%，去除误差偏离极大的数据点，复原精度优于90%。色卡b3的光谱信号整体较强，没有低响应光谱数据，光谱数据反演精度达到93.2%。
图 11 重构的光谱数据曲线和精度（黑色曲线：海洋光学光谱仪测试得到的目标谱线；红色曲线：文中实验系统重构的目标谱线）
Figure 11. Reconstructed spectral data curve and accuracy (Black curve: the target spectral curve measured by ocean optics spectrometer；Red curve: the target spectral curve recovered by the experimental system)
Double channels diffractive computational imaging spectrometer system
-
摘要: 常规衍射光谱成像系统采用单通道方案，主要针对简单图形目标或光谱特征已知的气体目标进行模拟仿真和光谱成像实验。而当目标为自然场景等复杂景物时，成像系统的光谱解算效果和精度难以保证。针对复杂景物成像，设计了一套双通道可见近红外衍射计算成像光谱仪系统，在常规单通道衍射成像光谱仪系统的基础上，增加一路全色相机成像，可以为衍射成像通道提供复杂景物的全色信息和先验知识。将两个通道的数据进行联合处理，提升最终的光谱数据反演效果和反演精度。介绍了系统组成和基本原理，分析了系统性能，利用仿真程序模拟了系统成像过程。在实验室搭建了可见近红外衍射计算成像光谱原理验证装置。对实验得到的450~800 nm的可见近红外混叠光谱数据进行光谱复原。利用海洋光学光谱仪测试色板的光谱曲线作为标准谱线，与复原得到的光谱数据进行对比，反演的光谱数据平均精度优于90%。通过衍射计算成像原理分析、模拟仿真和原理实验，验证了双通道衍射计算成像系统原理的正确性，能够反演得到精度优于90%的复杂景物光谱数据，提升了衍射成像光谱系统应用潜力和应用价值。Abstract: The conventional diffraction spectrum imaging system adopts the single channel scheme, which mainly carries out simulation and spectral imaging experiments for simple graphic targets or gas targets with known spectral characteristics. When the target is a complex scene such as natural scene, the spectral solution effect and accuracy of the imaging system are difficult to ensure. For the imaging of complex scenery, a dual channel visible and near-infrared diffraction computational imaging spectrometer system was designed. Based on the conventional single channel diffraction imaging spectrometer system, adding a panchromatic camera imaging coluld provide panchromatic information and a priori knowledge of complex scenes for diffraction imaging channels. The data of the two channels were jointly processed to improve the final spectral data inversion effect and inversion accuracy. The system composition and basic principle were introduced, the system performance was analyzed, and the imaging process of the system was simulated by using the simulation program. A verification device for the principle of visible and near-infrared diffractive computational imaging spectrometer system was built in the laboratory. Spectral restoration was carried out on the visible and near-infrared aliasing spectral data of 450-800 nm. Using the spectral curve of the color plate tested by ocean optics spectrometer as the standard spectral line, compared with the restored spectral data, the average accuracy of the retrieved spectral data was better than 90%. Through theoretical analysis, system simulation and imaging experiment, the correctness and feasibility of the system principle were verified. It can obtain better spectral solution effect and accuracy of complex scenery, and improve the application potential and application value of diffraction imaging spectral system.
-
Key words:
- spectral /
- diffractive /
- computational imaging /
- image restoration
-
图 1 衍射成像光谱系统示意图
Figure 1. Schematic diagram of diffraction imaging spectrometer system
图 3 仿真每个焦面处的混叠衍射图像
Figure 3. Each mixed diffractive image in corresponding focal plane
8 三个衍射通道与一个灰度通道的成像效果
8. Imaging effect of three diffraction channels and one grayscale channel
-
[1] Kar O F, Oktem F S. Compressive spectral imaging with diffractive lenses [J]. Optics Letters, 2019, 44(18): 4582. doi: 10.1364/OL.44.004582 [2] Skidanov R V, Blank V A, Morozov A A. Study of an imaging spectrometer based on a diffraction lens [J]. Computer Optics, 2015, 39(2): 218-223. doi: 10.18287/0134-2452-2015-39-2-218-223 [3] Michele Hinnrichs, Bradford Hinnrichs. Imaging spectroscopy using embedded diffractive optical arrays [C]//Proceedings of SPIE, 2017, 10402: 104020G. [4] Neelam Gupta. LWIR hyperspectral imager based on a diffractive optics lens [C]//Proceedings of SPIE, 2009, 7303: 730314. [5] Zhang Mingqi, Cao Guo, Chen Qiang, et al. Image restoration method based on improved inverse filtering for diffractive optic imaging spectrometer [J]. Computer Science, 2019, 46(1): 86-93. (in Chinese) [6] Liang Jingyu. Diffractive spectral imaging technology [D]. Hangzhou: Zhejiang University, 2012. (in Chinese) [7] Zeng Wenming, Chen Yuheng, Shen Weimin. Regularization image restoration algorithm for diffractive optic imaging spectrometer [J]. Opto-Electronic Engineering, 2014, 41(6): 45-50. (in Chinese) [8] Wang Xu, Chen Qiang, Sun Quansen. Multichannel spectral-spatial total variation model for diffractive spectral image restoration [J]. Journal of Computer Research and Development, 2020, 57(2): 413-423. (in Chinese) [9] Yang C, Edwards P, Shi K, et al. Proposal and demonstration of a spectrometer using a diffractive optical element with dual dispersion and focusing functionality [J]. Optical Letters, 2011, 36: 2023-2025. doi: 10.1364/OL.36.002023 [10] Blank V A, Skidanov R V. Diffraction lens in imaging spectrometer [J]. Computer Optics and Nanophotonics, 2015, 1490: 17-26. [11] Zhang Mingqi. Image restoration method based on improved inverse filtering for diffractive optic imaging spectrometer [D]. Nanjing: Nanjing University of Science and Technology, 2018. (in Chinese) [12] Wang Yefei, Cheng Yanping, Yao Yuan, et al. Design of membrane diffractive athermal infrared optical system [J]. Infrared Technology, 2021, 43(5): 422-428. (in Chinese) [13] Fan Bin, Liu Yanli, Zhao Haibo, et al. A new deep space hyperspectral diffraction computational imaging detection technology (Invited) [J]. Infrared and Laser Engineering, 2020, 49(5): 20201005. (in Chinese) doi: 10.3788/irla.5_invited-fanbin [14] Shao Xiaopeng, Su Yun, Liu Jinpeng, et al. Connotation and system of computational imaging (Invited) [J]. Acta Photonica Sinica, 2021, 50(5): 1-23. (in Chinese) [15] Zhang Chunmin, Mu Tingkui, Yan Tingyu, et al. Overview of hyperspectral remote sensing technology [J]. Spacecraft Recovery & Remote Sensing, 2018, 39(3): 104-114. (in Chinese) [16] Wang Baohua, Li Ke, Tang Shaofan, et al. Optical system design of a spaceborne imaging spectrometer with high resolution and super swatch [J]. Spacecraft Recovery & Remote Sensing, 2021, 42(1): 92-99. (in Chinese) [17] Wei Qing, Liu Jinming, Xu Qizhi. Panchromatic and multispectral image fusion by ratio enhancement based on classification and block [J]. Spacecraft Recovery & Remote Sensing, 2021, 42(5): 108-117. (in Chinese) -
点击查看大图
图(13)
计量
- 文章访问数: 224
- HTML全文浏览量: 28
- PDF下载量: 59
- 被引次数: 0
