下载:
-
光学三维测量技术具有非接触、精度高、速度快等特点，广泛应用于工业检测、逆向工程、生物医学等领域，主要分为被动式三维测量（如双目视觉）和主动式三维测量（如结构光）两大类[1]。数字条纹投影是一种主动式三维测量技术，该技术首先利用投影仪将特定形状的条纹投射至物体表面，同时利用摄像机采集调制后的条纹图像，然后将条纹图像传输至计算机进行条纹分析，便可以恢复出物体的三维形貌，目前已经成为三维测量领域的研究热点[2]。数字条纹的形状丰富多样，包括正弦条纹、二值条纹、三角条纹、梯形条纹等，其中正弦条纹应用最为广泛[3]。常用的条纹分析方法包括傅里叶变换法和相移法，其中傅里叶变换法只需要一幅条纹图像，测量速度较快；相移法需要多幅条纹图像，更适用于复杂形貌的三维测量。然而，上述两种方法只能计算得到截断相位，需要进一步进行相位展开，恢复出绝对相位[4]。目前常用的相位展开方法包括格雷码[5, 6]、相位编码[7, 8]、双频[9-11]和几何约束[12]等。格雷码法和相位编码法计算出的条纹级次容易与截断相位发生错位，引入相位展开误差[13]。相比而言，双频法使用低频相位对高频相位进行相位展开，避免了因条纹级次和截断相位的错位而引入的相位展开误差。传统双频法通过使用两组不同频率的相移条纹来计算高频相位和低频相位，因此需要2N≥6幅条纹图像[11]。根据双频法原理，Li等人[14]将高频条纹和低频条纹进行融合得到一种双频条纹，同样需要2N≥6幅条纹图像。Liu等人[15]提出一种改进的双频条纹，只需要五幅条纹图像，有效地提高了三维测量速度。与双频法类似，双频条纹相位展开的准确性受噪声影响较大[16]。几何约束法则根据条纹投影系统中摄像机与投影仪的几何约束关系，通过建立一个最小相位图实现相位展开，其优势在于无需额外的编码图像，但该方法只适用于深度变化范围较小的物体。
为了提高双频条纹的鲁棒性，文中提出了一种改进的双频几何约束条纹投影三维测量方法，其大致工作流程如下：首先，利用五步相移算法计算出高频相位和低频相位。然后，根据条纹投影系统的几何约束关系展开低频相位。最后，利用低频绝对相位对高频相位进行展开，重建出物体的三维形貌。仿真和实验结果均表明，改进的双频几何约束条纹具有较强的鲁棒性。
-
传统N ≥ 5步相移双频条纹，可表示为[15]：
$$\begin{split} & {I_n}(x,y) = A(x,y) + \\ &{B_{\rm{h}}}(x,y)\cos [{\phi _{\rm{h}}}(x,y) + 2{\text{π}} n/N] + \\ & {B_{\rm{l}}}(x,y)\cos [{\phi _{\rm{l}}}(x,y) + 4{\text{π}} n/N] \end{split} $$ (1) 式中：A表示图像背景强度；Bh和 Bl分别表示高频分量和低频分量的条纹调制度；ϕh和ϕl分别表示高频相位和低频相位,其计算公式如下：
$${\phi _{\rm{h}}}(x,y) = {\rm{arctan}}\left[ {\frac{{\sum\nolimits_{n = 1}^N {{I_n}\sin (2{\text{π}} n/N)} }}{{\sum\nolimits_{n = 1}^N {{I_n}\cos (2{\text{π}} n/N)} }}} \right]$$ (2) $${\phi _{\rm{l}}}(x,y) = {\rm{arctan}}\left[ {\frac{{\sum\nolimits_{n = 1}^N {{I_n}\sin (4{\text{π}} n/N)} }}{{\sum\nolimits_{n = 1}^N {{I_n}\cos (4{\text{π}} n/N)} }}} \right]$$ (3) 上式计算得到的ϕh
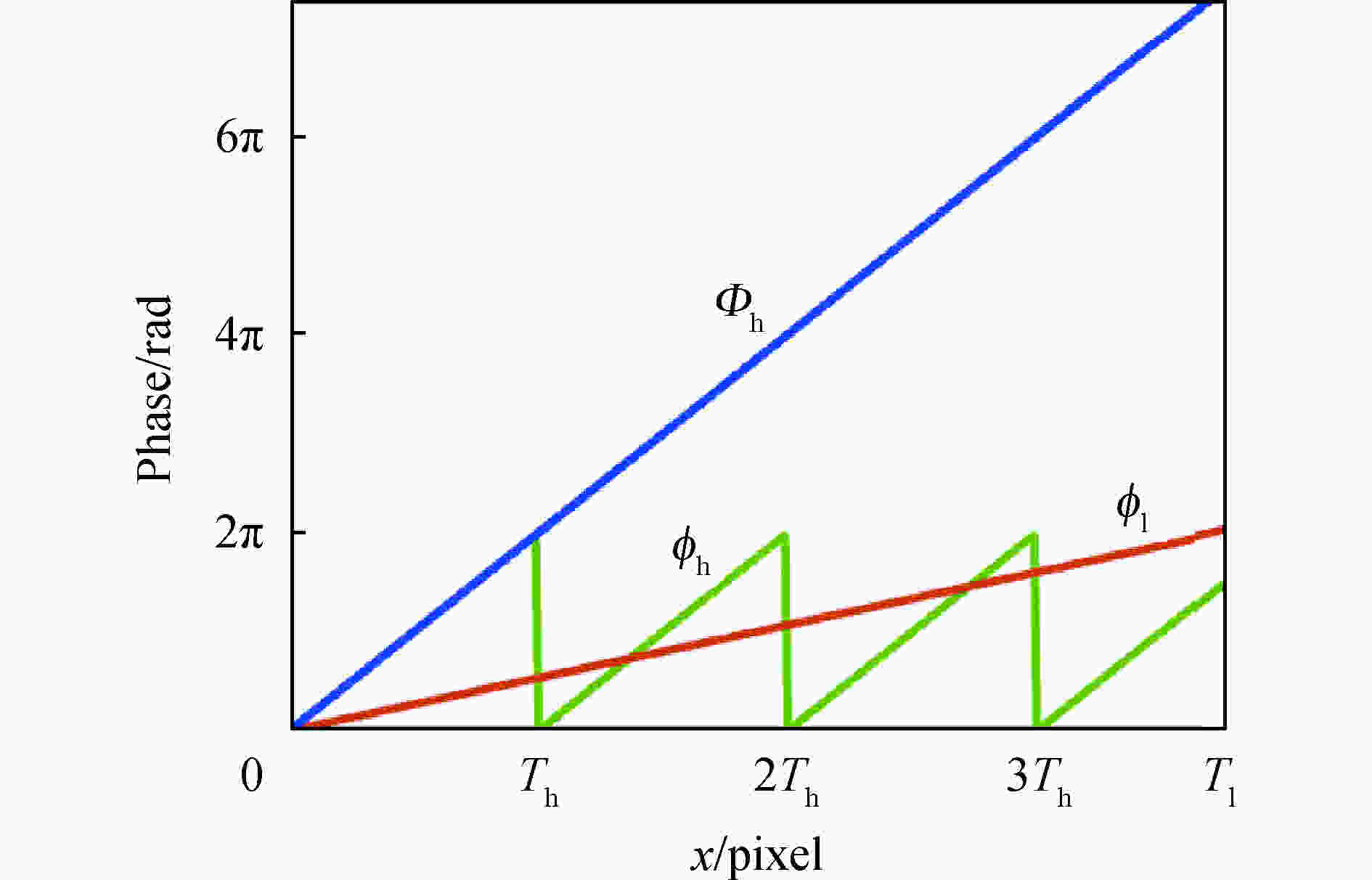
和ϕl的取值范围为(−π,+π]，因此ϕh和ϕl也称为截断相位，需要进行相位展开。假设ϕl只有一个周期，则Фl = ϕl。根据低频绝对相位Фl和高频绝对相位Фh的数学比例关系，可计算出ϕh所对应的条纹级次： $${K_{\rm{h}}}(x,y) = {\rm{round}}\left[ {\frac{{({f_{\rm{h}}}/{f_{\rm{l}}}) \times {\varPhi _{\rm{l}}} - {\phi _{\rm{h}}}}}{{2\pi }}} \right]$$ (4) 式中：fh和fl分别表示高频相位和低频相位的频率。进一步地，计算出： $${\varPhi _{\rm{h}}}(x,y) = {\phi _{\rm{h}}}(x,y) + 2{\text{π}} {K_{\rm{h}}}(x,y)$$ (5) 图1展示了传统双频条纹的相位展开原理，图中Th
和Tl分别表示ϕh和ϕl的周期。分析公式(4)得知, Фl参与计算时，需要放大γ = fh/fl 倍，这意味着Фl所包含的误差也放大了γ倍，容易导致部分 pixel 的Kh计算错误，进而引入相位展开误差至Фh。因此，传统双频条纹对噪声较为敏感，使得其应用范围受到了一定的限制。如何能够有效地降低比值γ，提高双频条纹的抗噪能力，是文中所要研究的内容。 
图 1 传统双频条纹相位展开
Figure 1. Phase unwrapping of traditional two-frequency fringe
-
对于测量范围内的某一物平面zmin，根据摄像机和投影仪的几何约束关系，可以建立该物平面的绝对相位图Фmin，称为最小相位图[12]。根据Фmin，可以对截断相位ϕ进行相位展开，其基本思想如图2所示。例如，在区间[A, B]内，满足条件0 < Фmin −ϕ < 2π，得到Ф = ϕ+2π；在区间[B, C]内，满足条件2π < Фmin −ϕ < 4π，得到Ф = ϕ+4π；依此类推，便可以将ϕ展开为Ф。因此，根据Фmin−ϕ的取值范围，便可以确定条纹级次。
图 2 几何约束相位展开
Figure 2. Phase unwrapping using geometric constraint
$$K = {\rm{ceil}}\left( {\frac{{{\varPhi _{{\rm{min}}}} - \phi }}{{2\pi }}} \right)$$ (6) 式中：ceil（）表示向上取整函数。需要注意，在相位域中，上述方法最大可测深度范围仅为2π。因此在实际测量过程中，被测物体需要尽可能地靠近物平面zmin。
-
针对传统双频条纹抗噪能力较差的问题，文中根据几何约束方法，对传统双频条纹进行改进，其相位展开原理如图3所示。改进双频条纹通过采用多个周期的低频相位(即fl >1)，能够有效地降低比值γ，提升双频条纹的抗噪能力。由于低频相位包含多个周期，低频相位ϕl将发生截断，因此需要首先展开ϕl，再用于展开高频相位ϕh。改进双频条纹进行三维测量的具体实现流程如下：首先，利用五步相移算法计算出ϕh和ϕl；然后，根据几何约束关系，恢复出ϕl所对应的最小相位图Фmin；根据公式(6)计算ϕl所对应的条纹级次Kl，并对ϕl进行相位展开得到Фl；最后根据公式(4)计算ϕh的条纹级次Kh，并对ϕh进行相位展开得到Фh。注意，若直接采用几何约束方法展开ϕh，将导致高频相位域中的最大可测深度范围仅为2π。相比而言，文中首先利用几何约束方法展开ϕl，然后利用Фl展开ϕh，在低频相位域中的最大可测深度范围为2π，转换至高频相位域中的最大可测深度范围将达到2πγ。
图 3 改进双频条纹相位展开
Figure 3. Phase unwrapping of modified two-frequency fringe
-
为了对比传统双频条纹和改进双频条纹的抗噪性能，文中进行了如下的仿真实验，其中仿真条纹图像的尺寸均为500×500 pixel。传统双频条纹的参数为：Th = 25 pixel, Tl = 500 pixel；改进双频条纹的参数为：Th = 25 pixel，Tl = 125 pixel。分别向仿真条纹图像中加入均值为0，标准差为σ = 0.03的高斯噪声，再对两组双频条纹进行相位展开。图4展示了传统双频条纹的仿真结果，图5展示了改进双频条纹的仿真结果。从图中可以看出，传统双频条纹恢复出的高频绝对相位曲线中出现了许多毛刺误差，主要是因为高斯噪声所引起的低频相位误差被放大了500/25 = 20倍，导致高频条纹级次计算错误；相比而言，改进双频条纹首先计算低频绝对相位，再计算高频绝对相位，高斯噪声所引起的低频相位误差被放大了125/25 = 5倍，保证了高频条纹级次计算的准确性，得到的高频绝对相位曲线比较光滑。上述仿真结果表明，与传统双频条纹相比，改进双频条纹的抗噪性能有了较大的提升。
图 4 传统的双频条纹仿真
Figure 4. Phase simulation of traditional two-frequency fringe
图 5 改进的双频条纹相位仿真
Figure 5. Simulation of modified two-frequency fringe
对于更一般的情况，通过改变比值γ和高斯噪声的标准差σ，探究不同噪声水平下，比值γ对相位展开的影响。图6展示了比值γ与错误展开的 pixel 数目M的关系曲线。当σ = 0.02时：若γ≤12，M趋近于0；若γ>12，M随着γ增加而增加。当σ = 0.03时：若γ≤7，M趋近于0；若γ>7，M随着γ增加而增加。当σ = 0.04时：若γ≤5，M趋近于0；若γ>5，M随着γ增加而增加。在相同噪声水平下：当γ取值较小时，M比较小；当γ较大时, M随着γ的增加而增加。因此，在实际应用中，需要根据条纹投影系统的噪声水平，选择合适的比值γ，保证三维测量的准确性。
图 6 不同高斯噪声水平(标准差σ)下，比值γ与错误展开的像素数目M之间的关系曲线
Figure 6. Relation curves between the ratio γ and the number of wrongly unwrapped pixels M under different levels (standard deviation σ) of Gaussian noises
-
为了进一步验证文中改进双频条纹的有效性，搭建了条纹投影实验平台，主要包括投影仪DLP Light-Crafter 4500和摄像机Point Grey Chameleon3，其中投影仪的分辨率为912×1 140 pixel，摄像机的分辨率为1 280×1 024 pixel。分别生成了传统双频条纹(Th = 20, Tl
= 912)和改进双频条纹(Th = 20, Tl = 100)，用于三维测量实验，并对比两种方法的测量结果。 首先，选择一个哆啦A梦模型作为测量物体，利用投影仪分别投射传统和改进的双频条纹至物体表面，摄像机同步采集被物体调制后的变形条纹图像。图7和图8
分别展示了传统双频条纹实验和改进双频条纹实验的部分图像。传统双频条纹实验中，直接使用低频绝对相位Фl = ϕl对高频截断相位ϕh 进行展开，恢复出高频绝对相位Фh；改进双频条纹实验中，首先利用最小相位图Фmin对低频截断相位ϕl进行展开得到Фl，然后再使用Фl对ϕh进行展开恢复出Фh。图9 展示了哆啦A梦的三维测量结果(相位分布)，可以看出，传统双频条纹重建出的三维形貌存在比较严重的毛刺误差，这主要是因为Фl对ϕh进行展开时，Фl所包含的相位误差被放大了912/20倍，导致条纹级次Kh计算错误；相比而言，改进双频条纹能够准确地重建出物体的三维形貌，在Фl对ϕh 进行展开时，Фl所包含的相位误差只被放大了100/20倍，有效地保证了Kh计算的准确性。 
图 7 传统的双频条纹实验
Figure 7. Experiment of traditional two-frequency fringe
图 8 改进的双频条纹实验
Figure 8. Experiment of modified two-frequency fringe
图 9 哆啦A梦的三维测量结果。(a) 传统的双频条纹；(b)改进的双频条纹
Figure 9. 3D shape measurement of the Doraemon. (a) Traditional two-frequency fringe; (b) modified two-frequency fringe
进一步地，选择一个球作为测量物体，分别采用传统双频条纹和改进双频条纹对其进行三维测量。图10展示了球的三维测量结果(相位分布)，可以看出，传统双频条纹重建出的球表面存在比较严重的毛刺误差。相比而言，改进双频条纹重建出的球表面比较光滑。上述两组实验结果均验证了改进双频条纹的有效性，相对于传统双频条纹，展现出更强的鲁棒性。
图 10 球的三维测量结果。(a) 传统的双频条纹；(b)改进的双频条纹
Figure 10. 3D shape measurement of the ball. (a) Traditional two-frequency fringe; (b) modified two-frequency fringe
-
针对传统双频条纹存在抗噪能力差的问题，文中提出了一种改进的双频几何约束条纹投影三维测量方法。该改进双频条纹的低频相位包含多个周期，通过条纹投影系统的几何约束关系展开低频相位，再用于展开高频相位，有效地提高了双频条纹的抗噪能力。同时分析了高频相位与低频相位的频率比值对相位展开的影响，得知频率比值越小，抗噪能力越强，但最大可测深度将会降低，因此在实际应用中应该根据不同场景选择合适的频率比值。仿真和实验结果均表明，与传统双频条纹相比，改进双频条纹的鲁棒性更高，具有更广阔的应用前景。
Modified dual-frequency geometric constraint fringe projection for 3D shape measurement
-
摘要:
双频条纹投影已经广泛应用于三维形貌测量，然而其相位展开的准确性受噪声影响较大。文中提出了一种改进的双频几何约束条纹，通过提高低频相位的频率，有效地提升了相位展开的鲁棒性。在三维测量过程中，首先，利用五步相移算法计算出双频条纹的高频相位和低频相位。然后，利用几何约束方法展开低频相位。最后，采用双频算法展开高频相位，进而重建出物体的三维形貌。仿真和实验结果均表明，相对于传统双频条纹，改进的双频条纹具有更高的鲁棒性和适用性。
Abstract:Dual-frequency fringe projection methods have been widely used in three-dimensional (3D) shape measurement, but the phase unwrapping is very sensitive to random noises. A modified dual-frequency geometric constraint fringe was presented. The robustness of phase unwrapping can be effectively enhanced by improving the frequency of low-frequency phase. During the 3D shape measurement, firstly, the five-step phase-shifting algorithm was used to extract two wrapped phases. Secondly, the low-frequency phase was unwrapped based on the geometric constraint method. Finally, the dual-frequency algorithm was used to unwrap the high-frequency phase, and then the 3D shape could be reconstructed. Both simulations and experiments demonstrate that the modified dual-frequency fringe is more robust and applicable than the traditional one.
-
Key words:
- dual-frequency fringe /
- phase-shifting /
- geometric constraint /
- phase unwrapping
-
图 6 不同高斯噪声水平(标准差σ)下，比值γ与错误展开的像素数目M之间的关系曲线
Figure 6. Relation curves between the ratio γ and the number of wrongly unwrapped pixels M under different levels (standard deviation σ) of Gaussian noises
图 9 哆啦A梦的三维测量结果。(a) 传统的双频条纹；(b)改进的双频条纹
Figure 9. 3D shape measurement of the Doraemon. (a) Traditional two-frequency fringe; (b) modified two-frequency fringe
-
[1] Su X, Zhang Q. Dynamic 3-D shape measurement method: A review [J]. Optics and Lasers in Engineering, 2010, 48(2): 191−204. doi: 10.1016/j.optlaseng.2009.03.012 [2] Zhang S. High-speed 3D shape measurement with structured light methods: A review [J]. Optics and Lasers in Engineering, 2018, 106: 119−131. [3] Zuo C, Feng S, Huang L, et al. Phase shifting algorithms for fringe projection profilometry: A review [J]. Optics and Lasers in Engineering, 2018, 109: 23−59. doi: 10.1016/j.optlaseng.2018.04.019 [4] Zhang S. Absolute phase retrieval methods for digital fringe projection profilometry: A review [J]. Optics and Lasers in Engineering, 2018, 107: 28−37. doi: 10.1016/j.optlaseng.2018.03.003 [5] Wu Z, Guo W, Zhang Q. High-speed three-dimensional shape measurement based on shifting Gray-code light [J]. Optics Express, 2019, 27(16): 22631−22644. doi: 10.1364/OE.27.022631 [6] He X, Zheng D, Qian K, et al. Quaternary gray-code phase unwrapping for binary fringe projection profilometry [J]. Optics and Lasers in Engineering, 2019, 121: 358−368. doi: 10.1016/j.optlaseng.2019.04.009 [7] Wang Y, Zhang S. Novel phase-coding method for absolute phase retrieval [J]. Optics Letters, 2012, 37(11): 2067−2069. doi: 10.1364/OL.37.002067 [8] Li Biao, Wu Haitao, Zhang Jiancheng, et al. 3D shape measurement method combining sinusoidal pulse width modulation fringe with phase coding fringe [J]. Infrared and Laser Engineering, 2016, 45(6): 0617006. (in Chinese) [9] Zhang M, Chen Q, Tao T, et al. Robust and efficient multi-frequency temporal phase unwrapping: optimal fringe frequency and pattern sequence selection [J]. Optics Express, 2017, 25(17): 20381−20400. doi: 10.1364/OE.25.020381 [10] Han Xu, Wang Lin, Fu Yanjun. Phase unwrapping method based on dual-frequency heterodyne combined with phase encoding [J]. Infrared and Laser Engineering, 2019, 48(9): 0913003. (in Chinese) [11] Hyun J, Zhang S. Enhanced two-frequency phase-shifting method [J]. Applied Optics, 2016, 55(16): 4395−4401. doi: 10.1364/AO.55.004395 [12] An Y, Hyun J, Zhang S. Pixel-wise absolute phase unwrapping using geometric constraints of structured light system [J]. Optics Express, 2016, 24(16): 18445−18459. doi: 10.1364/OE.24.018445 [13] Ma M, Yao P, Deng H, et al. A simple and practical jump error removal method for fringe projection profilometry based on self-alignment technique [J]. Review of Scientific Instruments, 2018, 89(12): 123109. doi: 10.1063/1.5051635 [14] Li J, Su H, Su X. Two-frequency grating used in phase-measuring profilometry [J]. Applied Optics, 1997, 36(1): 277−280. doi: 10.1364/AO.36.000277 [15] Liu K, Wang Y, Lau D, et al. Dual-frequency pattern scheme for high-speed 3-D shape measurement [J]. Optics Express, 2010, 18(5): 5229−5244. doi: 10.1364/OE.18.005229 [16] Zuo C, Huang L, Zhang M, et al. Temporal phase unwrapping algorithms for fringe projection profilometry: A comparative review [J]. Optics and Lasers in Engineering, 2016, 85: 84−103. doi: 10.1016/j.optlaseng.2016.04.022 -
点击查看大图
计量
- 文章访问数: 482
- HTML全文浏览量: 145
- PDF下载量: 71
- 被引次数: 0
