-
同步送粉激光熔覆技术是目前激光同步送料应用最为广泛的技术[1-4]。但由于金属粉末存在成本较高、粉速控制滞后、环境污染等缺点[5-7],近年来逐步发展了同步送丝激光熔覆方法。同步送丝激光熔覆方案又分侧向送丝和同轴送丝。熔覆成形对送丝姿态的要求非常高,不同的丝材送进方向、送进角和相对送进位置,所得到的熔道尺寸、表面粗糙度与形貌均会随之变化[8-9]。在侧向送丝状态下,由于丝材为单边受热,受热不均,易发生弯曲造成熔覆中断。同轴送丝的方法则可使丝材从中空光内部送进,光、丝同轴耦合,丝材周向均匀受热,获得的熔道各向同性[10-11]。然而,丝材为刚性材料,熔覆过程中若能量输入不足造成丝材无法同步熔化,丝材将在送丝推力和凝固层阻力作用下发生偏移,破坏熔池[11]。找出工艺参数的合理区间能够实现单道稳定熔覆;找出工艺参数和熔覆层几何形貌的映射关系能够结合闭环控制实现三维成形。
近年来,许多的学者尝试借助数据挖掘算法建模,寻求工艺参数和熔覆层形貌的定量模型。如J.Paulo Davim等用二次回归算法分析熔覆层宽度、高度、深度、润湿角和工艺参数的关系[12];;苏州大学史建军将能量和质量守恒定律以及回归算法结合分析熔覆层几何特征和工艺参数的关系[13];中国科学院姜淑娟等运用BP神经网络创建了高度预测模型[14]。查阅发现,目前对熔覆层形貌的预测多用少量样本建模,无法满足训练样本数至少多于网络权值2~10倍的标准[15],模型的泛化能力难以保证。此外,在模型的选取上,多用单一方式建模,未能体现不同方法建模的偏差。
文中采用“三分光束”光内送丝熔覆喷头[16-17]进行单因素单道熔覆实验,确定各工艺参数的工艺区间。以在各工艺区间随机抽样的方式,获得新的实验参数进行熔覆实验,得到更多的建模样本。将熔覆好的单道垂直扫描方向切开,将抛光后的照片导入AutoCAD测量其形貌尺寸,确保数据的可信度;选取BP神经网络和二次回归模型拟合样本数据,并对两种模型的预测能力与稳定性进行评价。文中的研究为光内送丝成形研究提供工艺窗口,可将训练好的模型可以作为成形系统的控制器或估计器,结合传感器在熔覆缺陷处通过调整加工参数,保证成形质量,为实现送丝熔覆过程的闭环控制打下基础。
-
实验设备为图1所示的“三分光束”光内送丝熔覆系统,其主要包括IPG-YLS系列光纤激光器、6轴KUKA机器手、“三分光束”光内送丝熔覆喷头、Miller-S-74S送丝机、制氮系统等。激光器产生的激光以及送丝机输出的丝材通过熔覆喷头在基体表面发生热耦合作用形成熔池。系统各部分在控制系统的协调下,分别在x,y,z方向上产生相应的位移,并带动熔覆喷头在二维平面内运动,形成单道熔覆层。
-
实验用基体材料为304不锈钢,熔覆前基体用酒精/丙酮去除油污,烘干备用。熔覆材料为FRN-ER50-6焊丝,其材料成分如表1所示。
表 1 FRN-ER50-6焊丝成分表
Table 1. Composition of FRN-ER50-6 welding wire
Composition C Mn Si P S Cu Fe Mass fraction 0.07% 1.53% 0.85% 0.011% 0.01% 0.12% Bal. -
同轴送丝激光熔覆过程中的物理化学过程非常复杂,根据加工特点和文献总结,确定激光功率(P)、扫描速度(Vs)、送丝速度(Vf)、离焦量(D)这四个工艺参数对熔覆层形貌的影响较为显著。
(1)激光功率的影响。当激光功率过小时,丝材熔化不充分易引起“断株”过渡;激光功率过大易引起“泪滴”过渡[1]。
(2)扫描速度的影响。扫描速度是指熔覆过程中喷头在加工路径上的移动速度。当扫描速度过小时,单位长度输入能量大,送进的丝材更多,所形成熔道宽高比小,易发生熔池重力克服表面张力引发熔池塌陷;当扫描速度过快时,单位长度输入能量小可能不能充分熔化所送进丝材。
(3)送丝速度的影响。送丝速度是指丝材在单位时间送进熔池的丝材的长度,它直接决定了熔覆层的体积。当送丝速度过快时,送进的丝材无法同步熔化,未熔丝材冲击基体破坏熔池。
(4)离焦量的影响。离焦量是指“三分光束”的交汇点与加工平面的法向距离,直接决定了热耦合区域的大小。
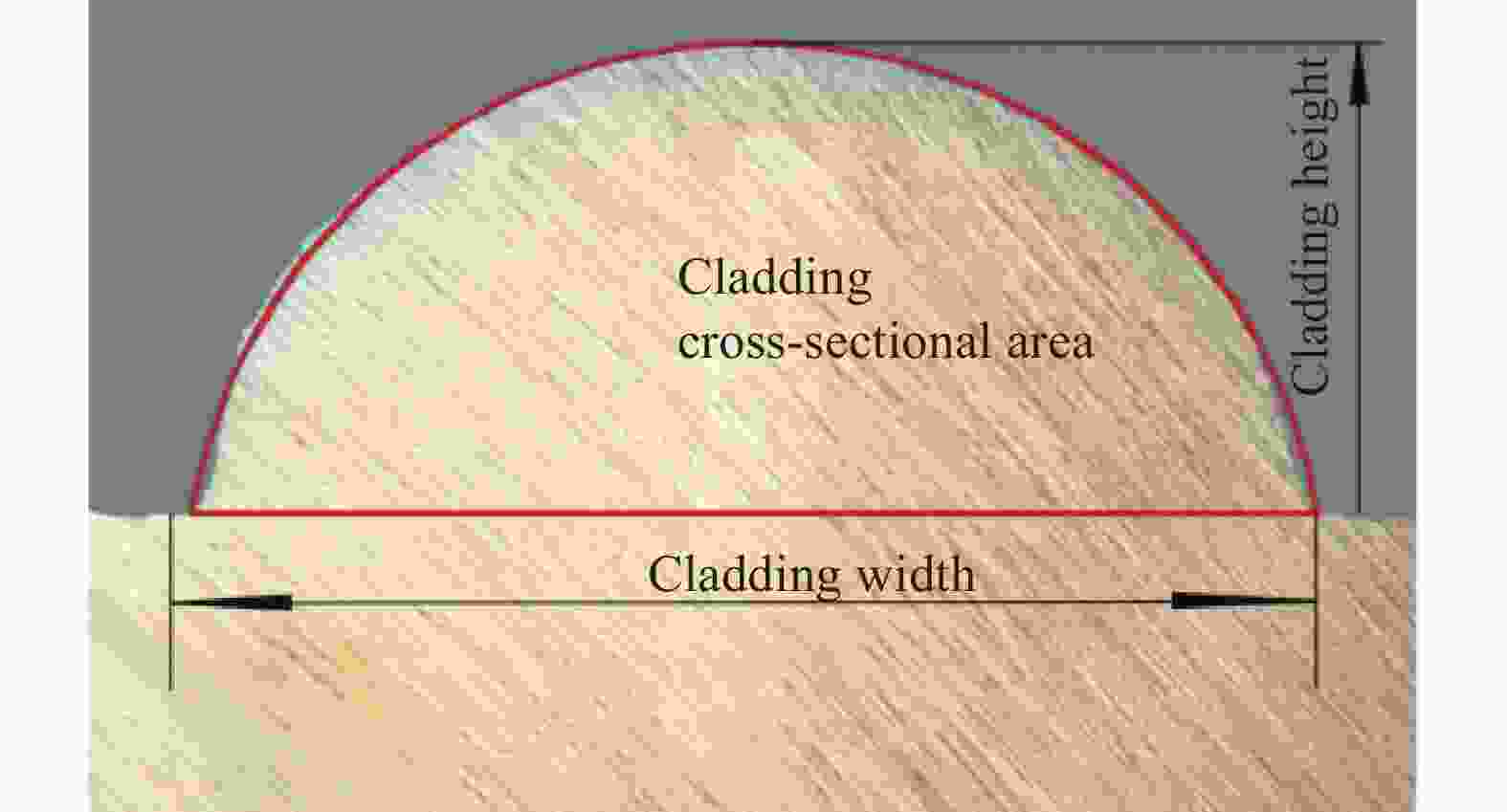
不同工艺参数的耦合共同决定熔覆层形貌。熔覆层形貌体现为熔覆层宽度(W)、高度(H)、横截面积(A),如图2所示。
基于以上讨论,文中欲建立的模型可以表述为:
$${{y = }}\left[ {{{W,H,A}}} \right]{{ = f}}\left( {{{P, }}{{V}_{s}}, {{V}_{f}}{{, D}}} \right)$$ (1) 式中:
$[W,H,A]$ 为因变量,分别为熔覆层宽度、高度、横截面积;$[P, V_{s}, V_{f}, D]$ 为自变量,分别为激光功率、扫描速度、送丝速度、离焦量。公式(1)表明,当映射关系f确定时,任意输入给定工艺参数都有唯一确定的熔覆层宽度、高度和截面积作为输出。
-
通过预实验,发现在激光功率为1 500 W,扫描速度为5 mm/s,送丝速度为14 mm/s,离焦量为−2 mm时能够成形液桥过渡、表面无缺陷的单道。基于上述先验实验参数设计表2单因素实验表。实验具体过程为:以激光功率、扫描速度、送丝速度、离焦量为变量,每次固定3个先验值参数(对应表2中fixed parameters列),调节另外一个参数(对应表2中varied parameter列)进行长40 mm的单道熔覆。“下探上搜”无法形成液桥过渡的该参数极限点,最后将其上下极限点作为该工艺参数的工艺区间(对应表2中Craft window列)。所得参数的工艺区间也即是所建模型的约束条件。
表 2 单因素实验表
Table 2. Single factor experiment table
Experiment Fixed parameters Varied parameter Craft window Laser power single factor
experimentScanning
velocity (Vs)Wire feeding
velocity (Vf)Defocus(D) Power(P) [1 300, 1 700 W] 5 mm/s 14 mm/s −2 mm 800 −1 800 W Scanning velocity single
factor experimentPower (P) Wire feeding
velocity(Vf)Defocus (D) Scanning velocity (Vs) [3, 7 mm/s] 1 500 W 14 mm/s −2 mm 2 −10 mm/s Wire feeding velocity
single factor experimentPower (P) Scanning
velocity (Vs)Defocus (D) Wire feeding
velocity(Vf)[9, 15 mm/s] 1 500 W 5 mm/s −2 mm 8 −20 mm/s Defocus single factor
experimentPower (P) Scanning
velocity (Vs)Wire feeding
velocity (Vf)Defocus (D) [−2.5, −1.5 mm/s] 1 500 W 5 mm/s 14 mm/s −5 −1 mm -
神经网络和回归都是基于数据驱动的模型,建模的数据量很大一部分决定模型泛化能力的强弱。基于单因素实验获得的各变量的工艺区间,使用MATLAB工具在工艺区间内生成服从均匀分布的80组工艺参数(公式(2))。对80组工艺参数进行长40 mm的单道熔覆,验证所得工艺区间的合理性的同时得到建模所需的样本。
$${{{X}}^{{(i)}}}{{ = }}\left[ {{{P}^{{(i)}}}, {{V}_{s}}^{{(i)}}, {{V}_{f}}^{{(i)}}, {{D}^{{(i)}}}} \right]{{ i = 1,2,3}},\cdots,{{80 }}$$ (2) 式中:X(i)为1×4的矩阵,每一行对应一个单道的工艺参数;
$\left[ {{P^{(i)}},\;{V_s}^{(i)},\;{V_f}^{(i)},\;{D^{(i)}}} \right]$ 分别对应第i个单道的所用的激光功率、扫描速度、送丝速度、离焦量,其值为工艺区间内的随机数值。 -
单因素实验得到激光功率介于1 300~1 700 W,扫描速度介于3~7 mm/s,送丝速度介于9~15 mm/s,离焦量介于−2.5~−1.5 mm时能够稳定获得液桥过渡、表面无缺陷单道。表3是随机参数实验生成的80个工艺参数的熔覆结果表。表3的
$\left[ {P,\;{V_s},\;{V_f},\;D} \right]$ 列是单道的工艺参数;$[W, H, A]$ 列是相应的熔覆层的宽度、高度和横截面积,该数值是通过AutoCAD软件的测量模块测得;单道熔覆照片一并置于表3的最后一列。表 3 各沉积单道的工艺参数及实验结果
Table 3. Process parameters and experimental results of each deposition single-track
Index P/W Vs/mm•s−1 Vf/mm•s−1 D/mm W/mm H/mm A/mm2 Cladding layer morphology 1 1 300.00 4.00 10.00 −2.50 3.45 1.14 2.81 
2 1 700.00 4.00 13.50 −1.75 3.85 1.14 2.99 
3 1 659.00 6.60 13.97 −2.32 3.64 0.68 1.67 
4 1 300.00 5.50 10.00 −2.50 3.37 0.80 1.93 
5 1 476.00 4.97 13.57 −1.55 3.31 1.17 2.78 
6 1 500.00 6.00 11.50 −2.50 3.63 0.82 2.09 
7 1 512.00 5.02 14.31 −1.83 3.20 1.10 2.56 
8 1 500.00 6.00 15.16 −2.50 3.33 1.10 2.50 
9 1 493.00 6.21 12.43 −1.66 3.09 0.79 1.71 
10 1 545.00 4.71 11.04 −2.17 3.40 1.06 2.56 
11 1 500.00 6.00 14.63 −2.50 3.36 0.94 2.09 
12 1 658.00 3.92 11.04 −1.87 3.54 1.17 3.02 
13 1 500.00 6.00 16.80 −2.50 3.31 1.21 2.74 
14 1 700.00 6.00 10.50 −2.00 3.73 0.68 1.72 
15 1 586.00 5.87 11.73 −2.15 3.84 0.83 2.19 
16 1 523.00 3.06 11.73 −1.83 3.62 1.45 3.97 
17 1 530.00 5.76 12.43 −2.09 3.30 0.85 1.95 
18 1 398.00 3.26 11.04 −1.61 3.38 1.37 3.40 
19 1 448.00 5.86 11.73 −2.04 3.13 0.88 1.95 
20 1 500.00 6.00 18.20 −2.50 3.24 1.34 2.93 
21 1 544.00 3.48 12.06 −2.07 3.35 1.32 3.25 
22 1 372.00 4.95 8.38 −2.02 3.92 0.71 1.93 
23 1 597.00 6.24 14.31 −2.11 3.38 0.96 2.33 
24 1 343.00 3.03 9.86 −1.98 3.50 1.23 3.14 
25 1 500.00 6.00 15.00 −1.50 3.44 1.02 2.49 
26 1 598.00 4.70 12.06 −2.29 3.58 1.04 2.63 
27 1 390.00 5.50 13.97 −1.95 3.10 1.01 2.23 
28 1 300.00 7.00 10.00 −2.50 3.31 0.63 1.49 
29 1 605.00 5.33 14.31 −1.54 3.08 1.04 2.32 
30 1 687.00 5.52 12.43 −1.51 3.35 0.88 2.08 
31 1 300.00 3.00 10.00 −2.50 3.59 1.32 3.54 
32 1 600.00 5.00 10.50 −2.25 3.59 0.85 2.10 
33 1 647.00 3.89 13.97 −2.22 3.54 1.31 3.23 
34 1 634.00 6.69 13.57 −1.94 3.42 0.87 2.06 
35 1 500.00 6.00 9.70 −2.50 3.51 0.69 1.71 
36 1 500.00 6.00 16.80 −2.50 3.39 1.07 2.41 
37 1 500.00 6.00 10.73 −2.50 3.74 0.74 1.92 
38 1 523.00 3.06 11.73 −1.83 3.27 1.44 3.59 
39 1 700.00 6.00 10.50 −2.00 3.53 0.70 1.70 
40 1 600.00 4.00 12.00 −1.50 3.94 0.95 2.61 
41 1 661.00 4.26 12.06 −1.56 3.54 1.10 2.91 
42 1 500.00 4.00 10.50 −2.50 3.73 0.73 1.86 
43 1 300.00 5.00 13.50 −1.50 3.48 0.99 2.37 
44 1 559.00 3.28 12.43 −1.60 3.42 1.34 3.38 
45 1 300.00 5.00 10.00 −2.50 3.26 0.93 2.18 
46 1 300.00 6.00 10.00 −2.50 3.42 0.74 1.83 
47 1 693.00 6.36 11.73 −2.18 3.34 0.82 1.90 
48 1 500.00 6.00 13.00 −2.50 3.64 0.74 1.90 
49 1 600.00 6.00 9.00 −1.75 3.26 0.62 1.42 
50 1 375.00 4.22 12.43 −2.05 3.18 1.15 2.64 
51 1 511.00 4.75 14.31 −1.72 3.27 1.22 2.87 
52 1 500.00 6.00 10.00 −2.50 3.60 0.76 1.90 
53 1 400.00 3.00 10.50 −1.50 3.48 1.27 3.22 
54 1 397.00 3.54 9.09 −2.40 3.34 1.00 2.35 
55 1 400.00 4.00 9.00 −2.25 3.52 0.85 2.10 
56 1 500.00 6.00 17.47 −2.50 3.33 1.12 2.57 
57 1 500.00 6.00 9.00 −2.50 3.27 0.69 1.61 
58 1 500.00 6.00 14.63 −2.50 3.42 0.88 2.15 
59 1 316.00 5.64 12.43 −2.41 3.44 0.87 2.10 
60 1 649.00 3.71 9.86 −2.05 3.45 1.00 2.45 
61 1 474.00 6.80 13.97 −2.28 3.44 0.64 1.48 
62 1 500.00 6.00 13.00 −2.50 3.55 0.88 2.11 
63 1 554.00 4.24 9.86 −1.68 3.49 0.97 2.38 
64 1 565.00 6.64 13.57 −1.83 3.02 0.95 2.01 
65 1 607.00 4.63 11.73 −2.17 3.27 1.08 2.52 
66 1 500.00 3.00 12.00 −1.50 4.10 1.17 3.35 
67 1 300.00 3.00 9.00 −2.50 3.65 1.01 2.55 
68 1 622.00 6.71 14.31 −1.84 3.23 0.90 2.00 
69 1 700.00 4.00 13.50 −1.75 4.03 1.10 3.13 
70 1 639.00 4.26 12.06 −1.93 3.50 1.08 2.69 
71 1 652.00 5.25 13.57 −1.68 3.45 1.07 2.64 
72 1 300.00 6.50 10.00 −2.50 3.59 0.70 1.74 
73 1 606.00 4.40 12.06 −2.07 3.62 1.07 2.70 
74 1 423.00 4.32 11.04 −2.32 3.45 1.04 2.53 
75 1 400.00 5.00 15.00 −1.75 3.53 1.08 2.66 
76 1 488.00 4.13 11.04 −2.40 3.48 0.95 2.23 
77 1 600.00 4.00 12.00 −1.50 3.96 0.85 2.38 
78 1 500.00 4.00 10.50 −2.50 3.79 0.79 2.10 
79 1 395.00 6.67 13.57 −1.83 3.15 0.82 1.77 
80 1 300.00 3.50 10.00 −2.50 3.75 1.20 3.25 
文中将采用表3的实验数据作为建模所需的样本。其中样本1~65作为训练集,样本66~80作为测试集。模型仅由训练集数据建立,建模完成后使用测试集的数据检验并评估模型的泛化能力。使用均方根误差RMSE、85%置信度预测的准确率ACC85%作为模型泛化能力的评价指标,定义如下:
$$RMSE = \sqrt {\sum\nolimits_i {{{\left( {\mathop {y_j^{{{(}}i{{)}}}}\limits^ \wedge - y_j^{(i)}} \right)}^2}} /n} ,\;\;\;0 \leqslant i \leqslant n,j = 1,2,3$$ (3) $$AC{C_{85\% }} = \frac{{\sum\limits_i {{\mathop{ Cond}\nolimits} _j^{(i)}} }}{n} \times 100\% ,\;\;\;0 \leqslant i \leqslant n,j = 1,2,3$$ (4) 其中
$${{Con}}{{{d}}^{(i)}} = \left\{ {\begin{array}{*{20}{c}} 1&{if|\mathop {y_{j}^{{(i)}}}\limits^ \wedge - y_{j}^{{(i)}}| \leqslant 15\% y_{j}^{{(i)}}} \\ 0&{\rm{else}} \end{array}} \right.$$ (5) 式中:
$\mathop {{{y}}_{j}^{{(i)}}}\limits^ \wedge $ 为第i个样本的j指标的预测值;j为1对应的指标为熔覆层的宽度;j为2对应熔覆层高度;j为3对应横截面积;${{y}}_{j}^{{(i)}}$ 为第i个样本j指标的实际测量值;n为样本的数量。 -
激光功率、扫描速度、送丝速度、离焦量对熔覆层的形貌的影响并非独立不相关,而是共同耦合作用影响熔覆层的形貌。它们呈复杂的非线性映射关系。二次回归通过引入变量间的交叉项来体现变量间的耦合。二次回归的模型可以表述为:
$$\mathop {{{{y}}_{j}}}\limits^ \wedge = {w_{j}}X,\;\;\;{j} = 1,2,3$$ (6) 式中:X是输入参数,其长度为21×1。它是由工艺参数
$\left( {P,\;{V_s},\;{V_f},\;D} \right)$ 的4个一次项、16个二次项及模型的常数项1组成;wj是待求系数,其长度为1×21。二次回归的目标是通过找到系数wj,使预测值$\mathop {{{{y}}_{j}}}\limits^ \wedge $ 和真实值${{{y}}_j}$ 的均方误差最小,即:$${{{w}}_j} = \mathop {arg\; \min }\limits_{{w_j}} {(\mathop {{y_j}}\limits^ \wedge - {y_j})^2},\;\;\;{j} = 1,2,3$$ (7) 将公式(6)代入公式(7)目标函数可改写为:
$${{{w}}_j} = \mathop {arg\; \min }\limits_{{w_j}} {({{{w}}_j}X - {y_j})^2},\;\;\;{j} = 1,2,3$$ (8) 令
${{E = }}{({{{w}}_j}X - {y_j})^2}{{ = (}}{{{w}}_{j}}X - {y_j}{)^{\rm{T}}}({{{w}}_{j}}X - {y_j})$ ,对wj求导得到:$$\frac{{\partial {{E}}}}{{\partial {{{w}}_j}}} = 2{X^{\rm{T}}}(X{w_j} - {y_j})$$ (9) 令上式为零可得wj最优解的闭式解:
$${{{w}}_j} = {({X^{\rm{T}}}X)^{ - 1}}{X^{\rm{T}}}{y_{j}}$$ (10) 将表3得到的65组训练集数据代入公式(10),剔除置信度低于85%的变量得到二次回归的模型。
$$\begin{split} {W_2} = & {{ 15}}.27 -0.010\;62P - 0.029\;6{V_f} + \\ & 4.18D + 0.000\;003{P^2} - 0.001\;26PD - \\ & 0.004\;76{V_s}^2 + 0.608{D^2} \end{split} $$ (11) $$ \begin{split} {H_2} = & 0.134 - 0.404{V_s} + 0.094\;4{V_f} - 1.415D + \\ & 0.000\;141P{V_s} + 0.000\;443PD + 0.027{V_s}^2 - \\ & 0.0213\;3{V_s}{V_f} + 0.003\;67{V_f}^2 - 0.189{D^2} \end{split} $$ (12) $$\begin{split} {A_2}= & 1.79 - 1.25{V_s} + 0.426{V_f} - \\ & 1.33D + 0.000\;32P{V_s} + 0.000\;851PD + \\ & 0.088\;8{V_s}^2 - 0.051\;1{V_s}{V_f} \end{split} $$ (13) 式中:(W2,H2,A2)分别为熔覆层宽度、高度和横截面积二次回归预测模型。给定工艺参数,可根据模型直接计算出熔覆层宽度,高度,横截面积的预测值。
-
BP(Back Propagation)神经网络由输入层、隐含层、输出层三部分构成。图3是同轴送丝熔覆BP神经网络拓扑结构图。
在同轴送丝激光熔覆中,4个可控变量共同影响熔层几何形貌,且有65组训练数据,故输入层是4×65的矩阵。隐含层层数、神经元个数、学习率等需调参确定。输出层为熔层宽度、高度、截面积。为使网络快速收敛,采用3个神经网络分别预测宽度、高度和截面积,故输出层是1×65的矩阵。连接权值由误差沿梯度负方向传播调整。
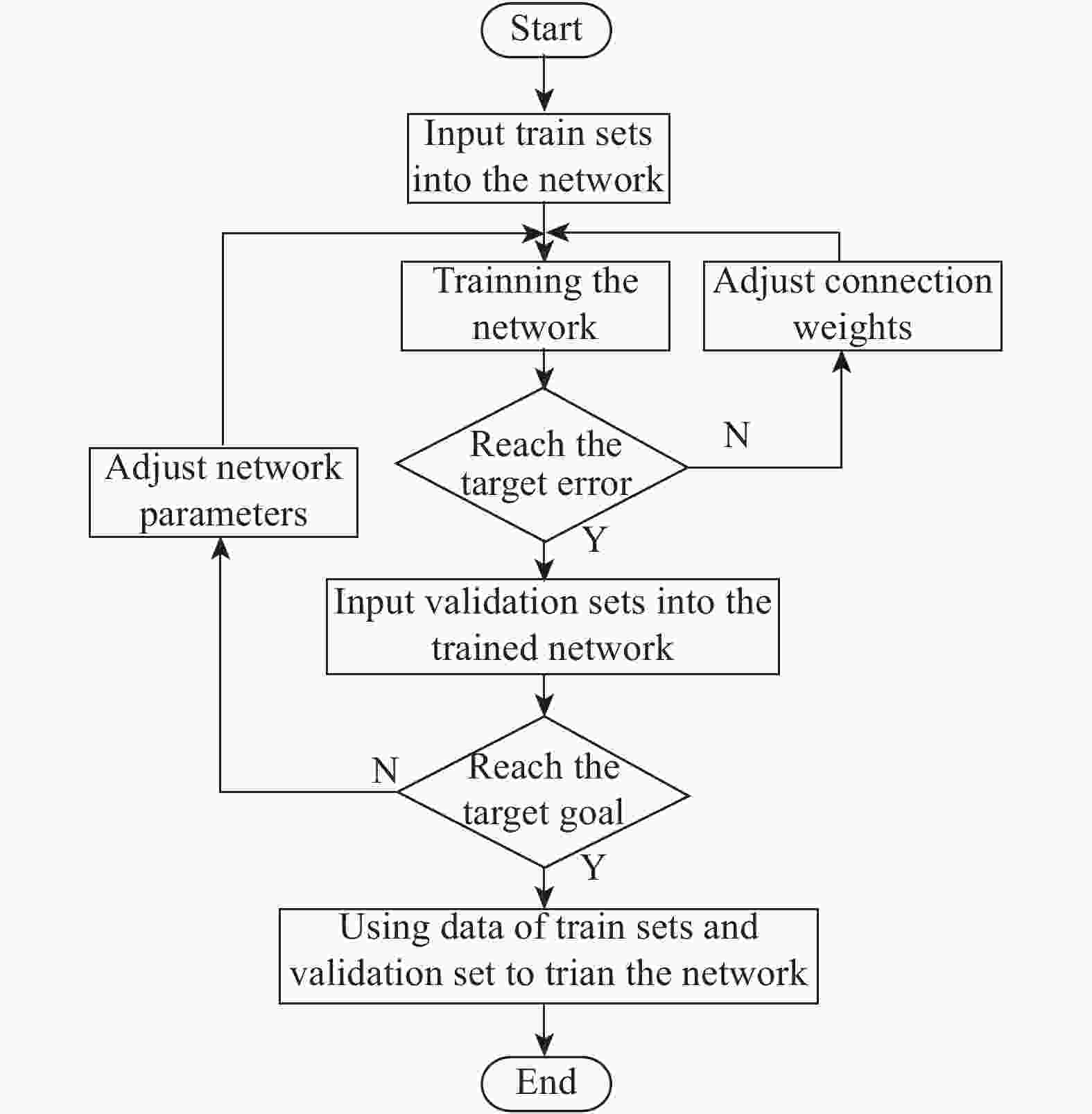
调参能降低过拟合增加神经网络预测的准确度[18]。调参策略如图4所示:将65组训练数据划分为50和15,分别作为训练集和验证集。验证集初始不训练,调参直至训练集训练的神经网络可在90%置信度下预测出验证集数据。随后用训练集和验证集共同训练调参完毕的神经网络模型,更新权值和阈值获得最终的模型。
调参完毕后各神经网络的参数如表4所示。
表 4 熔覆层宽度、高度和横截面积神经网络参数表
Table 4. Neural network parameter table of cladding width, height and cross-sectional area
Network parameter Width-BP Height-BP Cross-sectional
area-BPLearning rate 0.5 0.1 0.1 Maxium number of iterations 1 000 5 000 5 000 Training target error 0.01 0.01 0.01 The number of hidden neurous 3 4 4 Nodes of each hidden neurous $[8,8,10]$ $[6,10,10,6]$ $[7,12,12,6]$ -
文中基于均方根误差RMSE与85%置信度预测的准确率ACC85%作为模型预测能力的评价指标。取表3未用于建模15组数据作为测试集。将它们的工艺参数分别输入到二次回归模型和神经网络模型中,得到模型预测的熔覆层宽度、高度和横截面积。最后计算模型的预测值和实际值之间的RMSE与ACC85%。
图5中红色的线是实际测量的熔覆层宽度、高度和横截面积;蓝色的线是二次回归的预测值;黄色的线是BP神经网络的预测值。可以看出,神经网络的预测值在测量值上下波动幅值较小;二次回归模型的预测值的波动幅值较大。结合表5,神经网络模型在置信度为85%时,熔覆层宽度、高度、横截面积预测的准确率(ACC85%)分别达到100%,100%,93.3%;高于二次回归的100%,66.67%,73.33%。在均方根误差(RMSE)指标上神经网络的值为0.21,0.07,0.24;也优于二次回归的0.21,0.13,0.28。说明了神经网络预测的准确度优于二次回归。具体原因如下:

图 5 熔覆层宽度实际值与预测值对比(a)熔覆层高度实际值与预测值对比(b)熔覆层截面积实际值与预测值对比(c)
Figure 5. Comparison of cladding width actual value and predicted value(a), comparison of cladding height actual value and predicted value and area actual value (b), comparison of cladding predicted value(c)
表 5 二次回归模型和BP神经网络模型预测能力对比
Table 5. Comparison of prediction ability between quadratic regression model and BP neural network model
Method Predictive variable ACC85% RMSE Quadratic regression model Cladding width 100.00% 0.21 Cladding height 66.67% 0.13 Cladding area 73.33% 0.28 BP network model Cladding width 100.00% 0.21 Cladding height 100.00% 0.07 Cladding area 93.33% 0.24 二次回归模型(公式(6))通过引入变量的交叉项来体现熔覆过程多变量耦合的非线性过程,曾在同轴送粉中得到较好的熔覆层形貌预测模型[12,19]。但参考文献[12]、[19]固定了离焦量仅用3个工艺参数进行建模。对于同轴送丝激光熔覆,4个工艺参数对熔覆层形貌都有较大的影响,并且针对开发的同轴送丝激光熔覆系统,上述4个工艺参数都有较大的工艺窗口,故将4个工艺参数作为建模变量。由于4个工艺参数的耦合更为复杂,因此二次回归交叉项的假设过度简化了问题。神经网络模型的输出是各变量在隐含层神经元的非线性耦合的线性组合,非线性映射能力更强。对激光送丝熔覆的多变量耦合的解释性更高。因此,BP神经网络更适用于同轴送丝熔覆层形貌的预测。
-
(1) 研发的“三分光束”光内送丝熔覆系统具有较大的工艺窗口:激光功率1 300~1 700 W,扫描速度3~7 mm/s,送丝速度9~15 mm/s,离焦量−2.5~ −1.5 mm。在此参数范围内能够获得稳定液桥过渡、表面无缺陷的熔覆单道,避免了送丝熔覆最易出现的“断株”、“泪滴”、欠熔及过熔现象。
(2)建立了熔覆层形貌预测二次回归模型和BP神经网络模型,并进行了预测精度分析。其中针对熔覆层宽度、高度、横截面积的预测,BP神经网络的预测准确度ACC85%分别达到100%,100%,93.3%,均方根误差分别仅为0.21,0.07,0.24,优于二次回归模型的预测精度。神经网络相较二次回归更适用于同轴送丝激光熔覆熔覆层几何形貌的预测。文中为同轴送丝熔覆形貌预测提供了一种有效方法,并为后续开发熔覆过程闭环控制算法提供了参考。
Prediction of geometrical shape of coaxial wire feeding cladding in three-beam
-
摘要: 研究“三分光束”光内同轴送丝激光熔覆各工艺参数的工艺区间及参数与熔覆层几何形貌映射关系。首先,采用单因素实验方法研究激光功率、扫描速度、送丝速度、离焦量四个工艺参数的工艺区间;其次,以熔覆层的高度、宽度、横截面积作为熔覆层几何形貌的量化指标;最后,分别建立神经网络模型和二次回归模型实现熔覆工艺参数和熔覆层形貌量化指标之间映射关系的预测。基于单道单因素实验,当激光功率介于1 300~1 700 W,扫描速度介于3~7 mm/s,送丝速度介于9~15 mm/s,离焦量介于−2.5~−1.5 mm时能获得液桥过渡熔覆质量较好的单道。在对测试样本数据的预测中,在置信度85%情况下,BP神经网络模型对熔覆层高度、宽度、横截面积的预测精度分别为100%, 100%, 93.33%,均方根误差分别为0.21, 0.07, 0.24;二次回归模型的精度分别为100%, 66.67%, 73.33%,均方根误差分别为0.21, 0.13, 0.28。结论说明二次回归模型中变量的交叉项未能拟合送丝熔覆多变量耦合的非线性过程,而BP神经网络得到较好的预测结果。Abstract: The work aim to study parameters window of “three beam” coaxial wire feeding and the mapping relationship between parameters and cladding geometry. Firstly,the process interval of four process parameters of laser power, scanning speed, wire feeding speed and defocusing amount was studied by single factor experiment method; Secondly, the height, width and cross-sectional area of the cladding layer was used as the quantitative indicators of the geometry of the cladding layer; Finally, a neural network model and the quadratic regression model were set up respectively which were used to predict the mapping relationship between the cladding process parameters and the quantitative indicators of the cladding layer. Based on single-channel single-factor experiments, when the laser power was between 1 300 W and 1 700 W, the scanning speed was between 3 mm/s and 7 mm/s, the wire feeding speed was between 9 mm/s and 15 mm/s, and the defocusing amount was between −2.5 mm and −1.5 mm can get the cladding of liquid bridge transition with good quality. Besides, in the prediction of the test sample data, under the condition of 85% confidence, the prediction accuracy of the BP neural network model for the height, width and cross-sectional area of the cladding layer is 100%, 100%, 93.33%, and the root mean square error is 0.21,0.07,0.24. The accuracy of the quadratic regression model is 100%, 66.67%, and 73.33%, respectively, and the root mean square errors are 0.21, 0.13, and 0.28, respectively. From the result, the cross terms of the variables in the quadratic regression model failed to fit the nonlinear process of wire cladding. By contrast, BP neural network obtained better prediction results.
-
Key words:
- laser cladding /
- three bean /
- coaxial wire feeding /
- quadratic regression /
- BP neural network
-
表 1 FRN-ER50-6焊丝成分表
Table 1. Composition of FRN-ER50-6 welding wire
Composition C Mn Si P S Cu Fe Mass fraction 0.07% 1.53% 0.85% 0.011% 0.01% 0.12% Bal. 表 2 单因素实验表
Table 2. Single factor experiment table
Experiment Fixed parameters Varied parameter Craft window Laser power single factor
experimentScanning
velocity (Vs)Wire feeding
velocity (Vf)Defocus(D) Power(P) [1 300, 1 700 W] 5 mm/s 14 mm/s −2 mm 800 −1 800 W Scanning velocity single
factor experimentPower (P) Wire feeding
velocity(Vf)Defocus (D) Scanning velocity (Vs) [3, 7 mm/s] 1 500 W 14 mm/s −2 mm 2 −10 mm/s Wire feeding velocity
single factor experimentPower (P) Scanning
velocity (Vs)Defocus (D) Wire feeding
velocity(Vf)[9, 15 mm/s] 1 500 W 5 mm/s −2 mm 8 −20 mm/s Defocus single factor
experimentPower (P) Scanning
velocity (Vs)Wire feeding
velocity (Vf)Defocus (D) [−2.5, −1.5 mm/s] 1 500 W 5 mm/s 14 mm/s −5 −1 mm 表 3 各沉积单道的工艺参数及实验结果
Table 3. Process parameters and experimental results of each deposition single-track
Index P/W Vs/mm•s−1 Vf/mm•s−1 D/mm W/mm H/mm A/mm2 Cladding layer morphology 1 1 300.00 4.00 10.00 −2.50 3.45 1.14 2.81 2 1 700.00 4.00 13.50 −1.75 3.85 1.14 2.99 3 1 659.00 6.60 13.97 −2.32 3.64 0.68 1.67 4 1 300.00 5.50 10.00 −2.50 3.37 0.80 1.93 5 1 476.00 4.97 13.57 −1.55 3.31 1.17 2.78 6 1 500.00 6.00 11.50 −2.50 3.63 0.82 2.09 7 1 512.00 5.02 14.31 −1.83 3.20 1.10 2.56 8 1 500.00 6.00 15.16 −2.50 3.33 1.10 2.50 9 1 493.00 6.21 12.43 −1.66 3.09 0.79 1.71 10 1 545.00 4.71 11.04 −2.17 3.40 1.06 2.56 11 1 500.00 6.00 14.63 −2.50 3.36 0.94 2.09 12 1 658.00 3.92 11.04 −1.87 3.54 1.17 3.02 13 1 500.00 6.00 16.80 −2.50 3.31 1.21 2.74 14 1 700.00 6.00 10.50 −2.00 3.73 0.68 1.72 15 1 586.00 5.87 11.73 −2.15 3.84 0.83 2.19 16 1 523.00 3.06 11.73 −1.83 3.62 1.45 3.97 17 1 530.00 5.76 12.43 −2.09 3.30 0.85 1.95 18 1 398.00 3.26 11.04 −1.61 3.38 1.37 3.40 19 1 448.00 5.86 11.73 −2.04 3.13 0.88 1.95 20 1 500.00 6.00 18.20 −2.50 3.24 1.34 2.93 21 1 544.00 3.48 12.06 −2.07 3.35 1.32 3.25 22 1 372.00 4.95 8.38 −2.02 3.92 0.71 1.93 23 1 597.00 6.24 14.31 −2.11 3.38 0.96 2.33 24 1 343.00 3.03 9.86 −1.98 3.50 1.23 3.14 25 1 500.00 6.00 15.00 −1.50 3.44 1.02 2.49 26 1 598.00 4.70 12.06 −2.29 3.58 1.04 2.63 27 1 390.00 5.50 13.97 −1.95 3.10 1.01 2.23 28 1 300.00 7.00 10.00 −2.50 3.31 0.63 1.49 29 1 605.00 5.33 14.31 −1.54 3.08 1.04 2.32 30 1 687.00 5.52 12.43 −1.51 3.35 0.88 2.08 31 1 300.00 3.00 10.00 −2.50 3.59 1.32 3.54 32 1 600.00 5.00 10.50 −2.25 3.59 0.85 2.10 33 1 647.00 3.89 13.97 −2.22 3.54 1.31 3.23 34 1 634.00 6.69 13.57 −1.94 3.42 0.87 2.06 35 1 500.00 6.00 9.70 −2.50 3.51 0.69 1.71 36 1 500.00 6.00 16.80 −2.50 3.39 1.07 2.41 37 1 500.00 6.00 10.73 −2.50 3.74 0.74 1.92 38 1 523.00 3.06 11.73 −1.83 3.27 1.44 3.59 39 1 700.00 6.00 10.50 −2.00 3.53 0.70 1.70 40 1 600.00 4.00 12.00 −1.50 3.94 0.95 2.61 41 1 661.00 4.26 12.06 −1.56 3.54 1.10 2.91 42 1 500.00 4.00 10.50 −2.50 3.73 0.73 1.86 43 1 300.00 5.00 13.50 −1.50 3.48 0.99 2.37 44 1 559.00 3.28 12.43 −1.60 3.42 1.34 3.38 45 1 300.00 5.00 10.00 −2.50 3.26 0.93 2.18 46 1 300.00 6.00 10.00 −2.50 3.42 0.74 1.83 47 1 693.00 6.36 11.73 −2.18 3.34 0.82 1.90 48 1 500.00 6.00 13.00 −2.50 3.64 0.74 1.90 49 1 600.00 6.00 9.00 −1.75 3.26 0.62 1.42 50 1 375.00 4.22 12.43 −2.05 3.18 1.15 2.64 51 1 511.00 4.75 14.31 −1.72 3.27 1.22 2.87 52 1 500.00 6.00 10.00 −2.50 3.60 0.76 1.90 53 1 400.00 3.00 10.50 −1.50 3.48 1.27 3.22 54 1 397.00 3.54 9.09 −2.40 3.34 1.00 2.35 55 1 400.00 4.00 9.00 −2.25 3.52 0.85 2.10 56 1 500.00 6.00 17.47 −2.50 3.33 1.12 2.57 57 1 500.00 6.00 9.00 −2.50 3.27 0.69 1.61 58 1 500.00 6.00 14.63 −2.50 3.42 0.88 2.15 59 1 316.00 5.64 12.43 −2.41 3.44 0.87 2.10 60 1 649.00 3.71 9.86 −2.05 3.45 1.00 2.45 61 1 474.00 6.80 13.97 −2.28 3.44 0.64 1.48 62 1 500.00 6.00 13.00 −2.50 3.55 0.88 2.11 63 1 554.00 4.24 9.86 −1.68 3.49 0.97 2.38 64 1 565.00 6.64 13.57 −1.83 3.02 0.95 2.01 65 1 607.00 4.63 11.73 −2.17 3.27 1.08 2.52 66 1 500.00 3.00 12.00 −1.50 4.10 1.17 3.35 67 1 300.00 3.00 9.00 −2.50 3.65 1.01 2.55 68 1 622.00 6.71 14.31 −1.84 3.23 0.90 2.00 69 1 700.00 4.00 13.50 −1.75 4.03 1.10 3.13 70 1 639.00 4.26 12.06 −1.93 3.50 1.08 2.69 71 1 652.00 5.25 13.57 −1.68 3.45 1.07 2.64 72 1 300.00 6.50 10.00 −2.50 3.59 0.70 1.74 73 1 606.00 4.40 12.06 −2.07 3.62 1.07 2.70 74 1 423.00 4.32 11.04 −2.32 3.45 1.04 2.53 75 1 400.00 5.00 15.00 −1.75 3.53 1.08 2.66 76 1 488.00 4.13 11.04 −2.40 3.48 0.95 2.23 77 1 600.00 4.00 12.00 −1.50 3.96 0.85 2.38 78 1 500.00 4.00 10.50 −2.50 3.79 0.79 2.10 79 1 395.00 6.67 13.57 −1.83 3.15 0.82 1.77 80 1 300.00 3.50 10.00 −2.50 3.75 1.20 3.25 表 4 熔覆层宽度、高度和横截面积神经网络参数表
Table 4. Neural network parameter table of cladding width, height and cross-sectional area
Network parameter Width-BP Height-BP Cross-sectional
area-BPLearning rate 0.5 0.1 0.1 Maxium number of iterations 1 000 5 000 5 000 Training target error 0.01 0.01 0.01 The number of hidden neurous 3 4 4 Nodes of each hidden neurous $[8,8,10]$ $[6,10,10,6]$ $[7,12,12,6]$ 表 5 二次回归模型和BP神经网络模型预测能力对比
Table 5. Comparison of prediction ability between quadratic regression model and BP neural network model
Method Predictive variable ACC85% RMSE Quadratic regression model Cladding width 100.00% 0.21 Cladding height 66.67% 0.13 Cladding area 73.33% 0.28 BP network model Cladding width 100.00% 0.21 Cladding height 100.00% 0.07 Cladding area 93.33% 0.24 -
[1] Maurizio Motta, Ali Gökhan-demir, Barbara Previtali. High-speed imaging and process characterization of coaxial laser metal wire deposition [J]. Additive Manufacturing, 2018, 22: 497−507. doi: 10.1016/j.addma.2018.05.043 [2] 王聪, 石世宏, 方琴琴, 等. 空间多元密排扭曲薄壁件的激光熔覆成形研究[J]. 中国激光, 2017, 44(6): 102−111. Wang Cong, Shi Shihong, Fang Qinqin, et al. Research on laser cladding forming of close-packed multivariant twisty thin-wall parts [J]. Chinese Journal of Lasers, 2017, 44(6): 102−111. (in Chinese) [3] 沈婷, 石拓, 傅戈雁, 等. 变壁厚偏心圆环结构激光熔覆成型及闭环控制[J]. 中国激光, 2018, 45(3): 222−229. Shen Ting, Shi Tuo, Fu Geyan, et al. Laser cladding forming and closed-loop control of thickness-variable eccentric ring structure [J]. Chinese Journal of Lasers, 2018, 45(3): 222−229. (in Chinese) [4] 张锐, 石拓, 石世宏, 等. 不等高结构件激光近净成形闭环控制[J]. 中国激光, 2018, 45(3): 209−215. Zhang Rui, Shi Tuo, Shi Shihong, et al. Closed-loop control of laser engineered net Shaping of unequal-height parts [J]. Chinese Journal of Lasers, 2018, 45(3): 209−215. (in Chinese) [5] Baumers M, Dickens P, Tuck C, et al. The cost of additive manufacturing: machine productivity, economies of scale and technology-push [J]. Technological Forecasting and Social Change, 2016, 102: 193−201. doi: 10.1016/j.techfore.2015.02.015 [6] Bekker A C M, Verlinden J C. Life cycle assessment of wire + arc additive manufacturingcompared to green sand casting and CNC milling in stainless steel [J]. Clean Prod, 2018, 177: 438−447. doi: 10.1016/j.jclepro.2017.12.148 [7] 史建军, 石拓, 石世宏, 等. 激光光内送粉仰面熔覆工艺研究及优化[J]. 红外与激光工程, 2019, 48(3): 0306005. doi: 10.3788/IRLA201948.0306005 Shi Jianjun, Shi Tuo, Shi Shihong, et al. Process study and optimization of upward cladding by laser inside powder feeding [J]. Infrared and Laser Engineering, 2019, 48(3): 0306005. (in Chinese) doi: 10.3788/IRLA201948.0306005 [8] Waheed Ui Haq Syed. Effect of wire feeding direction and location in multiple layer diode laser direct metal deposition [J]. Applied Surface Science, 2015, 248: 518−520. [9] 朱进前, 凌泽民, 杜发瑞, 等. 激光熔丝增材制造温度场的红外热像监测[J]. 红外与激光工程, 2018, 47(6): 0604002. Zhu Jinqian, Ling Zemin, Du Farui, et al. Monitoring of laser metal-wire additive manufacturing temperature field using infrared thermography [J]. Infrared and Laser Engineering, 2018, 47(6): 0604002. (in Chinese) [10] 石世宏, 傅戈雁, 李龙, 等. 中空激光光内同轴送丝熔覆工艺的实现及其试验研究[J]. 中国激光, 2010, 37(1): 01026605. Shi Shihong, Fu Geyan, Li Long, et al. Realization and research of laser cladding with method of internal wire feeding through a hollow laser beam [J]. Chinese Journal of Lasers, 2010, 37(1): 01026605. (in Chinese) [11] 傅戈雁, 石世宏, 韩学磊. 环形激光光内同轴送丝焊接试验研究[J]. 中国激光, 2010, 37(8): 08208006. Fu Geyan, Shi Shihong, Han Xuelei. Test research of laser welding based on coaxial wire feeding through an annular laser beam [J]. Chinese Journal of Lasers, 2010, 37(8): 08208006. (in Chinese) [12] J Paulo Davim, Carlos Oliveira, Cardoso A. Predicting the geometric form of clad in laser cladding by powder using multiple regression analysis (MRA) [J]. Materials and Design, 2008, 29(2): 554−557. doi: 10.1016/j.matdes.2007.01.023 [13] Shi Jianjun, Zhu Ping, Fu Geyan, et al. Geometry characteristics modeling and process optimization in coaxial laser inside wire cladding [J]. Optics and Laser Technology, 2018, 101: 341−348. doi: 10.1016/j.optlastec.2017.10.035 [14] 姜淑娟, 刘伟军, 南亮亮. 基于神经网络的激光熔覆高度预测[J]. 机械工程学报, 2009,3:269. Jiang Shujuan, Liu Weijun, Nan Liangliang. Laser cladding height prediction based on neural network[J]. Journal of Mechinical Engineering, 2009,3:269.(in Chinese) [15] Yi X, Tan C H, Siew C K. A new block cipher based on chaotictent maps [J]. IEEE Transcations on Circuits and System, 2002, 49(12): 1826−1829. doi: 10.1109/TCSI.2002.805714 [16] 傅戈雁. 一种用于激光熔覆的激光光内送丝装置: CN 105562951[P]. 2016-02-03 [17] 傅戈雁. 激光熔覆装置: CN 107627002[P].2017-09-20 [18] 周志华. 机器学习[M]. 北京: 清华大学出版社, 2016. Zhou Zhihua. Machine Learning[M]. Beijing: Tsinghua University Press, 2016.(in Chinese) [19] 朱萍. 同轴送丝激光熔覆工艺研究及薄壁墙成形堆积[D]. 苏州: 苏州大学, 2013. Zhu Ping. Study on inside-laser coaxial wire feeding process of laser cladding and single beads prototyping[D]. Suzhou: Soochow University, 2013.(in Chinese) -







 下载:
下载: